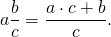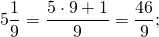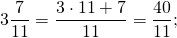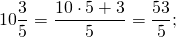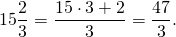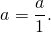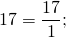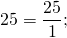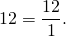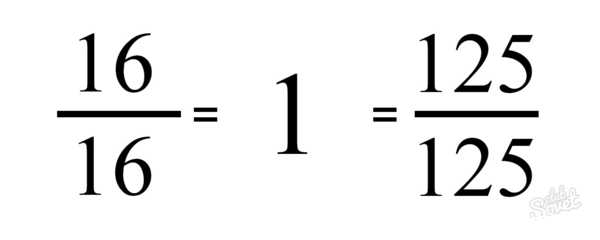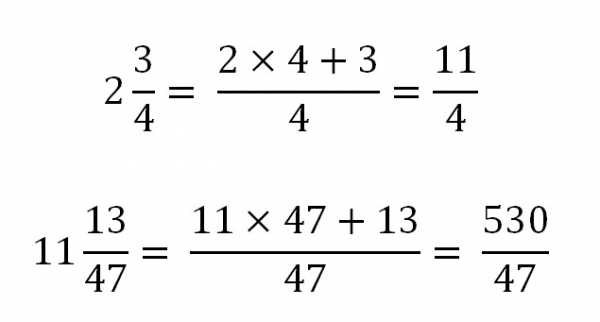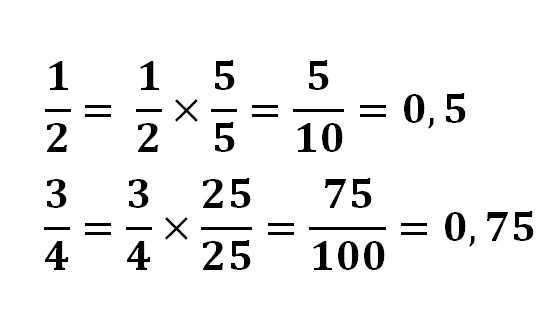Как из смешанной дроби сделать обыкновенную

Смешанные дроби

Что такое смешанная дробь

Число, содержащее в себе целую и дробную части, называется смешанной дробью.

По сути, данное понятие представляет собой сумму целого числа и правильной дроби:

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Превращение смешанной дроби в неправильную

Любое смешанное число можно преобразовать в неправильную дробь. Для этого необходимо к произведению целой части и знаменателя дробной части прибавить числитель. Полученная сумма будет числителем неправильной дроби, а знаменатель останется прежним.

Преобразование смешанной дроби в неправильную можно записать в виде формулы:

Выполнение действий со смешанными дробями, формулы и примеры

Сложение

Чтобы посчитать сумму смешанных дробей необходимо отдельно сложить их целые компоненты и дробные составляющие. Правильные дроби в составе смешанных чисел суммируются при помощи приведения к наименьшему общему знаменателю.

Формульное выражение сложения смешанных чисел:

\(a\frac bc+d\frac ef=\left(a+d\right)+\left(\frac bc+\frac ef\right)\)

Вычисляем наименьший общий знаменатель дробных слагаемых:

Вычитание

Чтобы из одной смешанной дроби вычесть другую, нужно дробные компоненты уменьшаемого и вычитаемого привести к минимальному общему знаменателю, затем выполнить вычитание отдельно целых и дробных частей.

Формула для ситуации, когда дробь в составе уменьшаемого больше, чем дробная часть вычитаемого:

\(a\frac bc-d\frac ef=\left(a+\frac bc\right)-\left(d+\frac ef\right)\;=\left(a-d\right)+\left(\frac bc-\frac ef\right)\)

В случае, когда дробь в составе уменьшаемого меньше дроби в составе вычитаемого, необходимо меньшую дробь превратить в неправильную, отняв единицу от целой части уменьшаемого, то есть:

\(a\frac bc-d\frac ef=\left(\left(a-d\right)-\frac ef\right)+\frac bc\)

Для решения этого выражения найдем наименьший общий знаменатель:

8=2×2×2, следовательно, 8 — это наименьший общий знаменатель.

Умножение и деление

Перед тем, как умножать или делить смешанные числа, необходимо преобразовать их в неправильные дроби. После этого можно производить нужное действие по правилам умножения и деления обыкновенных дробей.

Формула умножения смешанных чисел выглядит так:

Формула деления смешанных дробей:

При умножении смешанной дроби на натуральное число преобразование в неправильную дробь делать не нужно. Такого рода вычисления производятся с помощью распределительного закона умножения.

Если требуется разделить смешанную дробь на натуральное число или натуральное число на смешанную дробь, нужно представить делимое и делитель в виде неправильной дроби, затем выполнить необходимое действие, как с обыкновенными дробями.

Если нужно выполнить умножение или деление смешанной дроби на обыкновенную дробь, смешанное число необходимо преобразовать в неправильную дробь. После преобразований нужное действие производится по такому же алгоритму, как с обыкновенными дробями.

Как смешанное число перевести в неправильную дробь

Вопрос о том, как перевести смешанное число в неправильную дробь, возникает как при умножении и делении смешанных чисел, так и в качестве самостоятельного задания.

Чтобы смешанное число перевести в неправильную дробь, надо:

1) Целую часть умножить на знаменатель и к произведению прибавить числитель. Результат записать в числитель.

2) Знаменатель переписать без изменения.

С помощью схемы перевод смешанного числа в неправильную дробь можно изобразить так:

Теперь рассмотрим, как смешанное число перевести в неправильную дробь, на конкретных примерах.

А как целое число записать в виде неправильной дроби? Для этого достаточно представить его в виде дроби, числитель которой равен данному числу, а знаменатель — единица. С помощью схемы перевод целого числа в неправильную дробь можно изобразить так:

Примеры записи целого числа в виде неправильной дроби:

39 Comments

СУПЕР САЙТ БОЛЬШОЕ СПАСИБО РАЗРАБОТЧИКАМ!Я ПОНЯЛ. КЛАССНЫЙ САЙТ.

Спасибо,очень помогли,всё доступно объяснили

Пожалуйста! 🙂 Успехов Вам!

Meley! Желаю Вам дальнейших успехов в учебе!

Самый лучший сайт, забыл как преобразовать смешанную дробь в неправильную и с вашим сайтом все понял

Сайт просто супер всё понятно класс

классный сайт. отдельное большое спасибо всем разработчикам!!

Спасибо, Вова!
Я надеюсь, сайт поможет Вам освоить математику на «отлично».

супер-пупер спасибо большое я по математике получила 12 благодаря вам.
meley:
10.02.2014 в 15:23 (Изменить)

Светлана Иванова благодаря вам я стала отличницей и все у меня спрашивают в классе как ты стала отличницей а я говорю благодаря Светлане Ивановой

Перевод периодической дроби в обыкновенную дробь

Содержание

Периодические дроби – очень интересное явление. Только представьте себе дробь, у которой нет конца, и её «хвост» длится и длится. В рамках этого урока мы расскажем, как сделать перевод периодических дробей в обыкновенные. Сначала рассмотрим состав чистых и смешанных периодических дробей, а затем — запись периодической дроби в виде примера, ведь знак дроби означает знак деления.

Состав периодической дроби

Прежде чем мы начнём превращать периодические дроби в обыкновенные, нам необходимо разобраться, как называются части периодических дробей. Это нам понадобится.

Итак, на первом месте – целая часть периодической дроби.

Всё, что после запятой, будет дробной частью.

У чистых периодических дробей дробная часть состоит из периода (повтораяющейся части дроби). Она взята в скобки. В скобках может быть не одна, а несколько цифр. Количество цифр в скобках называется длиной периода.

В смешанной периодической дроби между запятой и периодом есть ещё одна или несколько цифр. Эти цифры в период не входят, то есть не повторяются. Надо сказать, что в разных пособиях эта часть дроби может называться по-разному. Иногда ей не дают никакого названия, и просто пишут «цифры между запятой и периодом». Но также эту часть называют непериодической частью или предпериодом.

Перевод чистых периодических дробей в обыкновенные дроби

С чистыми периодическими дробями (то есть с теми, у которых период начинается сразу после запятой) всё очень просто. Для них существует простой алгоритм.

После того, как дробь записана, её можно сократить, разделив числитель и знаменатель на одинаковое число.

Перевод смешанных периодических дробей в обыкновенные дроби

Со смешанными дробями дело обстоит сложнее, тут нужно запомнить более длинный алгоритм действий. Кроме того, нужно хорошо знать названия всех частей периодической дроби, чтобы не запутаться.

Для перевода смешанной периодической дроби в обыкновенную нужно:
1) записать целую часть дроби (если она есть) без изменений
2) записать в виде числителя разность дробной части периодической дроби (записываем её без скобок, как если бы это было натуральное число) и предпериода (непериодической части) дроби
3) записать в виде знаменателя число, состоящее из девяток и нулей, где число девяток равно длине периода, а нулей – длине предпериода.

Выглядит очень длинно и сложно! Но проделав подобные вычисления несколько раз, вы сможете выполнять их без особого труда.

Целую часть записываем без изменений, переходим к дробной.

Разберём ещё один пример.

В знаменателе пишем одну девятку, так как длина периода равна одному, и два ноля, так как в непериодической части дроби у нас две цифры.

Уже после того, как вы переведёте несколько периодических дробей в обыкновенные, вы почувствуете, что алгоритм запомнился и уже не кажется таким сложным. Также хорошо проверять свои вычисления при помощи калькулятора, разделяя числитель полученной дроби на знаменатель.

Математические дроби – просто о сложном

В статье описаны математические дроби: основные виды дробей, их основное свойство, а также все операции, которые можно выполнять с дробями (сокращение, приведение, сравнение, сложение, вычитание, умножение и деление).

Дробь и ее виды

Правильная — дробь, у которой числитель меньше знаменателя (например, 1/5, 2/9).

Неправильная — дробь, у которой числитель больше или равен знаменателю (например, 7/2, 5/5).

Смешанная — дробь, записанная в виде целого числа и правильной дроби. Она представляет собой сумму этого числа и дроби. Любую неправильную дробь можно перевести в смешанную путем выделения целой части (например, 9/4 = 2 ¼).

Десятичная — дробь со знаменателем 10, 100, 1000 и т.д. (например, 7/10 или 0,7; 9/100 или 0,09). Десятичная дробь записывается в виде целой и дробной части, которые отделяются запятой.

Математические дроби: основное свойство

Если числитель и знаменатель умножить или разделить на одинаковое число (не ноль), то получится равная дробь. Например, 2/3 = 2*2 / 3*2 = 4/6

Сокращение дроби

Сокращение осуществляется с помощью основного свойства дроби (чтобы упростить ее вид).

Чтобы сократить математические дроби, нужно разделить числитель и знаменатель дроби на НОД.

НОД – это наибольший общий делитель (то есть максимальное число, на которое делится и числитель, и знаменатель). Например, для дроби 4/20 наименьшим общим делителем будет 4 (4/20 = 1/5).

Приведение дробей к общему знаменателю

Любые две дроби можно привести к общему знаменателю. Обычно дроби приводят к наименьшему общему знаменателю (НОК) – минимальное число, которое делится на каждый знаменатель.

Например, для дробей 1/4 и 1/3 общий знаменатель общий знаменатель равен 12, для дробей 1/6 и 1/3 общий знаменатель будет 6).

Для приведения дроби к общему знаменателю нужно:
1. Найти общий знаменатель – НОК (для дробей 1/6 и 1/9 общий знаменатель будет равен 18);
2. Найти множитель для каждой дроби – разделить общий знаменатель на знаменатель исходной дроби (для дроби 1/6 множитель будет равен 3 (18:6=3), для дроби 1/9 – 2 (18:9=2)).
3. Умножить числитель дроби на множитель (для дроби 1/6 получаем 1*3/6*3=3/18, для дроби 1/9 получаем 2*1/2*9=2/18)

Преобразование неправильной дроби в смешанную дробь и обратно

Любую неправильную дробь можно перевести в смешанную (рассмотрим на примере 14/3).
Для перевода необходимо выполнить деление числителя на знаменатель с остатком (14 разделить на 3 равно 4 и остаток 2): получавшаяся целая часть от деления (число 4) – целая часть дроби, остаток от деления (число 2) – числитель правильной дроби. Получаем число 4 2/3.
На примере пирога: каждый пирог разрезан на 3 части и всего есть 14 кусочков. Получаем, что 12 кусочков составляют 4 целых пирога и еще остается два кусочка).

Для перевода смешанной дроби в неправильную необходимо (рассмотрим на примере 4 2/3):
для получения числителя целую часть дроби умножить на знаменатель и прибавить исходный числитель (4 умножить на 3 и прибавить 2, получим 14); знаменатель оставить прежним (число 3).
На примере пирога: есть 4 целых пирога, разрезанных на 3 части, и еще 2 кусочка из трех; получаем 12 кусочков из пирогов, разрезанных на три части, и 2 кусочка из пирога, разрезанного на три части. Итого, получаем 14 кусочков пирогов, каждый из которых разрезан на три части.

Математические дроби: сравнение

Если сравнивать две математические дроби с одинаковыми знаменателями, то больше та дробь, числитель которой больше (например, 5/6 > 1/6, то есть пять частей из шести будет больше, чем одна часть из шести).

Если сравнивать две математические дроби с одинаковыми числителями, то больше та дробь, знаменатель которой меньше (например, 1/2 > 1/3, то есть 1/2 часть пирога будет больше, чем 1/3).

Чтобы сравнить две обыкновенные дроби, следует привести дроби к общему знаменателю и сравнить числители получившихся дробей (например, для сравнения 3/4 и 5/6 нужно привести дроби к общему знаменателю; получаем 9/12

Как перевести обыкновенную дробь в неправильную дробь в – Как преобразовать смешанную в неправильную дробь

Как смешанное число перевести в неправильную дробь

Вопрос о том, как перевести смешанное число в неправильную дробь, возникает как при умножении и делении смешанных чисел, так и в качестве самостоятельного задания.

Чтобы смешанное число перевести в неправильную дробь, надо:

1) Целую часть умножить на знаменатель и к произведению прибавить числитель. Результат записать в числитель.

2) Знаменатель переписать без изменения.

С помощью схемы перевод смешанного числа в неправильную дробь можно изобразить так:

Теперь рассмотрим, как смешанное число перевести в неправильную дробь, на конкретных примерах.

А как целое число записать в виде неправильной дроби? Для этого достаточно представить его в виде дроби, числитель которой равен данному числу, а знаменатель — единица. С помощью схемы перевод целого числа в неправильную дробь можно изобразить так:

Примеры записи целого числа в виде неправильной дроби:

Светлана МихайловнаОбыкновенные дроби

Как правильно перевести правильную дробь в неправильную дробь

Каждый современный человек в школьную бытность во время решения математических задач нередко сталкивался с разнообразными задачками на дроби. Их достаточно много, потому имеет смысл рассмотреть различные варианты решения самых основных подобных задач.

Как перевести дроби

Виды дробей

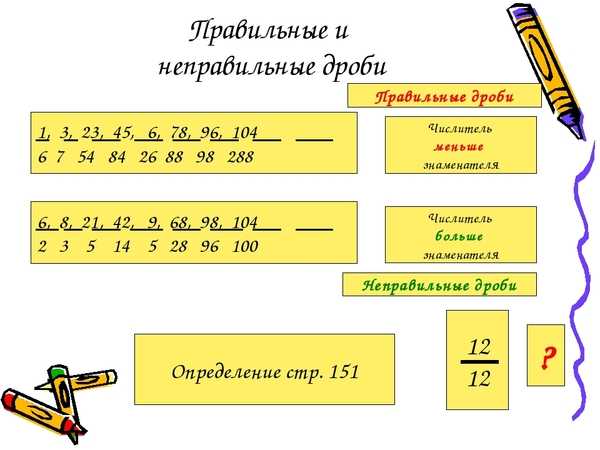
Правильные и неправильные дроби

Верхнее число у любой дроби носит название числителя, в то время, как нижнее число – это знаменатель. Обыкновенные дроби — это частные от двух чисел, причем, одно из этих них находится в числителе у дроби, а второе, соответственно, является знаменателем этой дроби. Виды таких обыкновенных дробей определяются сравнением значений их знаменателя и числителя.

Правильная дробь

В том случае, когда знаменатель у дроби является натуральным числом, которое по своему значению больше ее числителя, также натурального числа, то дробь носит название правильной. Примерами таких могут быть: 8/19; 9/14; 31/162; 5/37 и так далее.

Как перевести дробь

Неправильная дробь

Если же знаменатель у дроби меньше, либо же равен ее числителю, то такая дробь уже называется неправильной. Например, это такие, как: 7/4; 19/6; 15/3; 231/83 и тому подобные.

Неправильная дробь

Зачем переводится неправильная дробь в правильную?

Такая математическая манипуляция необходима, если выполняется действие с несколькими дробями, например, их слагают.

Если есть смешанная дробь, то сначала ее следует перевести в неправильную, потом уже выполнять другие математические действия.

Переведение в неправильную дробь

Чтобы какую-нибудь смешанную дробь превратить в неправильную, потребуется, для начала, целую ее часть умножить на знаменатель ее дробной части, а потом добавить числитель к данному произведению. Далее сумма берется, как числитель, но при том же самом, что и прежде знаменателе. Для осуществления перевода неправильной дроби в правильную, потребуется числитель такой неправильной дроби поделить на ее знаменатель. Далее, полученное таким путем целое число следует взять целой частью дроби, в то время, как остаток, если он, конечно, есть, сделать числителем дробной части у правильной дроби. Знаменатель пишется тот же самый, что и был. Чтобы перевести какую-либо неправильную дробь в десятичную, надо сначала выяснить, существует ли вообще такой множитель, который позволяет привести знаменатель ее дробной части в неправильном формате к числу, которое равняется десяти или десятке, возведенной в любую степень. То есть, 10, 100, 1000 и так далее. Если же такой множитель имеется, то следует умножить как числитель, так и знаменатель у неправильной дроби на данный множитель, тем самым как бы проверяя его. А после умноженный числитель потребуется через запятую приписать к целой части у неправильной дроби.

Нельзя перевести с округлением до десятых

В том случае, когда подобного множителя, как такового, не существует, это обозначает, что такая неправильная дробь не имеет четкого эквивалента в десятичной форме. Проще говоря, далеко не каждую из неправильных дробей представляется возможным перевести, сделав десятичной. В таком случае, потребуется найти приблизительное, максимально соответствующее значение дроби. Тут все зависит от требуемой в условии той ли иной задачи степени точности. Просчитать данную дробь проще всего на калькуляторе, но можно это также в уме или банально в столбик. Например, «41/7 = 5(6/7) = 5,9», это с округлением до десятых, или «= 5,86», когда требуется округлять до сотых, а также «= 5,857», если действует округление до тысячных. Многие из дробей четко в десятичные не переводятся, потому считать их проще не в уме и не в столбик, а посредством калькулятора.

Без манипуляций с дробями не представляется возможным ни один школьный курс математики. Да и в повседневности редко приходится иметь дело лишь с целыми числами, а потому переводить правильные дроби в неправильные, либо превращать в такие смешанные дроби нужно уметь каждому. Это очень просто и потому запомнить, как следует это делать, можно буквально после пары практических примеров, решенных на бумаге, а затем и вообще — в уме. С десятичными дробями ситуация несколько иная и не все можно точно перевести в десятичный вид.

Математические дроби

Неправильные дроби

Перевод неправильной дроби в смешанное число

Для перевода неправильной дроби в смешанное число выполните следующие шаги:

Рассмотрим на примерах как переводить неправильные дроби в смешанные числа.

Пример Перевести неправильные дроби в смешанные числа.

Перевод смешанного числа в неправильную дробь

Для перевода смешанного числа в неправильную дробь выполните следующие шаги:

Пример Перевести смешанные числа в неправильные дроби.

Как перевести неправильную дробь в десятичную дробь 🚩 как перевидить неправильные дроби в десятичные 🚩 Математика

Дробь представляет собой число, которое состоит из одной или нескольких долей единицы. В математике существует три вида дробей: обыкновенные, смешанные и десятичные.

Обыкновенная дробь записывается как соотношение, в котором в числителе отражается, сколько взято частей от числа, а знаменатель показывает, на сколько частей разделена единица. Если в дроби числитель меньше знаменателя, то перед нами правильная дробь.Например: ½, 3/5, 8/9.

Если числитель равен знаменателю или больше его, то мы имеем дело с неправильной дробью. Например: 5/5, 9/4, 5/2 При делении числителя на знаменатель может получиться конечное число. Например, 40/8 = 5. Следовательно, любое целое число может быть записано в виде обыкновенной неправильной дроби или ряда таких дробей. Рассмотрим пример записи одного и того же числа в виде ряда различных неправильных дробей.

В общем виде смешанная дробь может быть представлена формулой:

Таким образом, смешанная дробь записывается как целое число и обыкновенная правильная дробь, а под такой записью понимают сумму целого и его дробной части.

Десятичная дробь – это особая разновидность дроби, у которой знаменатель может быть представлен как степень числа 10. Существуют бесконечные и конечные десятичные дроби. При записи этой разновидности дроби сначала указывается целая часть, затем через разделитель (точку или запятую) фиксируется дробная часть.

Запись дробной части всегда определяется ее размерностью. Десятичная запись выглядит следующим образом:

Смешанную дробь можно перевести только в неправильную. Для перевода необходимо целую часть привести и тому же знаменателю, что и дробную. В общем виде это будет выглядеть следующим образом: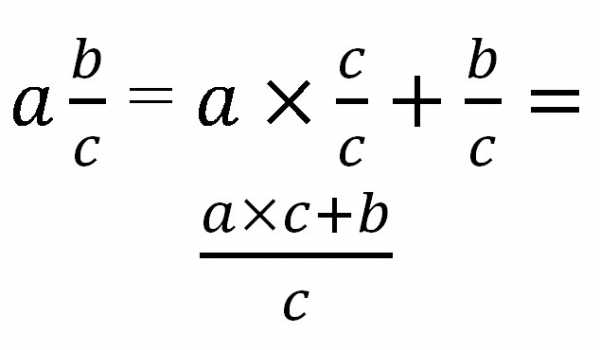Рассмотрим использование этого правила на конкретных примерах:

Неправильную обыкновенную дробь можно превратить в смешанную путем простого деления, в результате которого находится целая часть и остаток (дробная часть).

Для примера переведем дробь 439/31 в смешанную:​​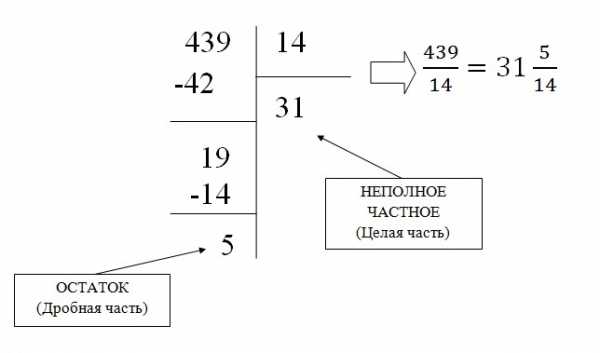

В некоторых случаях перевести дробь в десятичную достаточно просто. В этом случае применяется основное свойство дроби, числитель и знаменатель умножаются на одно и то же числу, для того, чтобы привести делитель к степени числа 10.

В некоторых случаях может понадобиться найти частное путем деления уголком или с помощью калькулятора. А некоторые дроби невозможно привести к конечной десятичной дроби. Например, дробь 1/3 при делении никогда не даст конечный результат.

Преобразование неправильной дроби в смешанное число

Любой неправильный дробь можно представить в виде натурального числа или суммы натурального числа и правильной дроби:

Для преобразования неправильной дроби в смешанное число необходимо:

Примеры преобразования неправильной дроби в смешанное число

Пример 1: Преобразовать неправильный дробь (выделить полную часть):

Целая часть равна 3, а остаток — 2

Пример 2: Преобразовать неправильный дробь (выделить полную часть):

Целая часть равна 67, а остаток — 1

Пример 3: Превратить неправильный дробь (выделить полную часть):

Целая часть равна 13, а остаток — 2

Преобразование обыкновенной дроби в десятичную

На практике чаще используют десятичные дроби, но, когда в задаче встречаются и обыкновенные, и десятичные дроби, то следует перейти к одному виду дробей (перевести десятичные дроби в обыкновенные или обыкновенные в десятичные). Не всегда обыкновенную дробь можно перевести в десятичную, поэтому десятичный переводят в обычный.

При переводе десятичной дроби в обычный в числителе дроби записывают число,
что стоит после запятой, а разрядная единица в знаменателе ( и т.д.) содержит столько же нулей, сколько знаков после запятой в десятичной дроби.

Пример 4: Переведите обыкновенную дробь в десятичную

Если десятичная дробь содержит целую часть, то его переводят в смешанное число и целую часть записывают перед дробной:

Как перевести неправильную дробь?

Каждый человек при решении задач с математики нередко сталкивался с задачами на дроби. Их очень много, поэтому мы рассмотрим разные варианты решения основных таких задач.

Что такое дроби

Верхнее число любой дроби называется числителем, а нижнее число — знаменателем. Обыкновенная дробь — это частное двух чисел, одно из этих чисел — в числителе дроби, второе — в знаменателе дроби. Виды этих обыкновенных дробей будут определяться сравнением знаменателя и числителя дроби.

Ежели знаменатель дроби (натуральное число) больше числителя дроби (натуральное число), то дробь называется правильной. Приведем примеры: 7/19; 9/13; 31/152; 5/17.

Если знаменатель дроби (натуральное число) меньше или равен числителю дроби (натуральное число), то дробь называется неправильной. Приведем примеры: 7/5; 19/3; 15/9; 231/63.

Как перевести неправильную дробь

Чтобы смешанную дробь перевести в неправильную, необходимо целую часть дроби умножить на знаменатель в дробной части и добавить числитель к этому произведению. Потом сумму взять как числитель, написав тот же, что и прежде знаменатель. Приведем примеры:

Для перевода неправильной дроби в правильную, необходимо числитель этой неправильной дроби разделить на ее знаменатель. Полученное, при этом, целое число взять целой частью дроби, ну а остаток (конечно, если он есть) взять как числитель дробной части правильной дроби, написав тот же, что и прежде знаменатель. Приведем примеры:

Для перевода неправильной дроби в десятичную необходимо выяснить, существует ли такой множитель, что позволит привести знаменатель дробной части неправильной дроби к числу, которое равно десятке (или десятке, которая возведена в любую степень (10, 100, 1000 и дальше). Если такой множитель есть, то необходимо умножить числитель и знаменатель неправильной дроби на этот множитель, чтобы проверить его. Теперь умноженный числитель необходимо приписать через запятую к целой части неправильной дроби. Приведем примеры:

Как 0,75 перевести в неправильную дробь?

75 раздели на 100 и получишь 75 стотых или по другому 3 четвёртых

3/4, только эта дробь называется обыкновенной, в неправильную ее нельзя перевести

Этого нельзя сделать т. к 75/100 правильная дробь

Я согласен с Светой Серовой

это обыкновенная дробь 3/4, 75/100 сократили числитель и знаменательна 25=3/4

нужно поменять местами числитель и знаменатель, и в этом случае получим неправильную дробь

Дроби и действия с дробями

Что такое дроби?

Вспоминаются примеры из начальной школы. Представьте себе пирог вкусный такой, и 4 голодных ребенка.

Как бы им так сделать, чтоб пирога досталось всем? Верно, надо его поделить, поделить один пирог на 4 человека:

На рисунке ты видишь пирог, разрезанный на 4 дольки. Так вот, как раз дробь – это и есть доля от целого.

Сегодня мы разберем подробно, что такое дроби. Как их правильно делить, умножать, вычитать, складывать, преобразовывать…

В общем, сегодня ты узнаешь о дробях ВСЕ, что нужно знать для успешной сдачи ОГЭ или ЕГЭ.

Дроби — коротко о главном

Определения:

Простая дробь (обыкновенная дробь) – запись рационального числа в виде отношения двух чисел \(\displaystyle\frac\).

Делимое \(\displaystyle a\) – числитель дроби, а делитель \(\displaystyle b\) – знаменатель дроби.

Правильная дробь – дробь, у которой числитель меньше знаменателя.

Например: \(\displaystyle\frac<2><5>\), \(\displaystyle\frac<1><7>\) и так далее.

Неправильная дробь –дробь, у которой числитель больше или равен знаменателю.

Например: \(\displaystyle\frac<9><5>\), \(\displaystyle\frac<13><2>\) и так далее.

Смешанная дробь – дробь, записанная в виде целого числа и правильной дроби и понимается как сумма этого числа и дроби.

Например: \(\displaystyle2\frac<2><5>\)\( \displaystyle \displaystyle=\frac<2\cdot 5><5>+\frac<2><5>=\frac<10><5>+\frac<2><5>=\frac<12><5>\).

Десятичная дробь – обыкновенная дробь со знаменателем \(\displaystyle10\), \(\displaystyle100\), \(\displaystyle1000\) и так далее, (т.е. \(\displaystyle<<10>^>\), где \(\displaystyle n\) — натуральное число).

Например: \(\displaystyle\frac<9><100>\) в виде десятичной дроби записывается как \(\displaystyle0,09\),

\(\displaystyle\frac<225><1000>\) записывается как \(\displaystyle0,225\).

Основное свойство дроби:

Если числитель и знаменатель дроби умножить или разделить на одно и то же число, дробь не изменится, несмотря на то, что выглядеть она будет по-другому.

Действия с дробями:

Сложение/вычитание дробей

Умножение дробей

Деление дробей

Сокращение дроби

Приведение дробей к наименьшему общему знаменателю

Например: \(\displaystyle\frac<1><3>\) и \(\displaystyle\frac<3><4>\). Наименьший общий знаменатель — \(\displaystyle12\).

Дополнительный множитель первой дроби — \(\displaystyle12:3=4\), дополнительный множитель второй дроби — \(\displaystyle12:4=3\).

Следовательно: для первой дроби: \(\displaystyle\frac<1\cdot 4><3\cdot 4>=\frac<4><12>\), для второй дроби: \(\displaystyle\frac<3\cdot 3><4\cdot 3>=\frac<9><12>\).

Преобразования неправильной дроби в смешанную дробь

Например: \(\displaystyle\frac<17><4>\) = \(\displaystyle4\frac<1><4>\).

Сравнение дробей:

Простые дроби

В данном случае от целого куска в сторонке отделенная одна доля, одна из четырех, одна четвертая.

Это простая дробь.

Простые дроби принято записывать одним из следующих способов: \(\displaystyle \frac<1><4>\), \(\displaystyle <1>/<4>\;.\)

Ты не поверишь, все эти записи означают одно и то же – одна четвертая. А что останется если забрать эту \(\displaystyle 1/4?\) Было \(\displaystyle 4\) из \(\displaystyle 4\), или \(\displaystyle 4/4\), забрали \(\displaystyle 1/4\).

Верно, останется \(\displaystyle 3\) дольки, \(\displaystyle 3\) из \(\displaystyle 4\). Запишем, как полагается, \(\displaystyle 3/4\).

Можно даже вот так: \(\displaystyle 4/4-1/4=3/4\)

То, что находится выше черты – это числитель (ну или слева от черты в такой записи как тут), то, что ниже – знаменатель.

Можно запомнить так: Ч – чердак. Числитель сверху 🙂

Примеры простых дробей: \(\displaystyle 1/5,\text< >2/4,\text< >3/10,\text< >17/3.\)

Правильные и неправильные простые дроби

В этом ряду все дроби правильные, в них числитель меньше знаменателя. Кроме одной. Да-да, ты не ошибся, бывает и такое, что числитель больше знаменателя, как в этой дроби, например: \(\displaystyle 17/3\).

Если числитель больше знаменателя, то дробь называется неправильной.

Вне зависимости от того правильная дробь или неправильная, она будет простой.

Давай остановимся на неправильной дроби \(\displaystyle 17/3\). Что же это она неправильная?

Вспоминай пример с пирогом, там была \(\displaystyle 1/4\) – одна часть из четырех, а тут что получается? \(\displaystyle 17\) частей из \(\displaystyle 3\)?

Бред какой-то! У нас в знаменателе число, которое означает, что весь пирог состоит из стольки частей! Берем \(\displaystyle 4\) части и поучаем целый ровненький пирог. Но числитель говорит, что на данный момент у нас есть лишь одна из этих частей.

А \(\displaystyle 17/3\)?

Что же, у нас есть \(\displaystyle 17\) частей, а для целого пирога в данном случае надо \(\displaystyle 3\) части. Ну так давай соберем из кусочков целые пироги и отдельно их поставим.

Как узнать сколько пирогов мы можем получить из \(\displaystyle 17\) частей? Верно, надо на \(\displaystyle 3\) как раз и поделить.

Если попробовать составить \(\displaystyle 6\) пирогов, т.е. \(\displaystyle 3\cdot 6=18\), надо \(\displaystyle 18\) частей. Не хватает. А \(\displaystyle 3\cdot 5=15\), о, хватило! Получается \(\displaystyle 5\) целых пирогов собрали, положили в сторону. Осталось \(\displaystyle 17-3\cdot 5=2,2\), \( \displaystyle 2\) куска.

А для целого пирога надо \( \displaystyle 3\) части. В итоге у нас \( \displaystyle 5\) целых и \( \displaystyle 2/3\) (две третьих) пирога.

Много места занимает такое обозначение. А что если убрать лишние слова и оставить только \( \displaystyle 5\frac<2><3>\) (пять целых и две третьих).

Смешанная дробь

То, что у нас получилось (\( \displaystyle 5\frac<2><3>\)), называют смешанная дробь – дробь, записанная в виде целого числа и правильной дроби и понимается как сумма этого числа и дроби.

То, что между \( \displaystyle 5\) пирогами и \( \displaystyle 2/3\) пирога нет никакого знака не говорит о том, что там знак умножения, как если бы мы писали \( \displaystyle 2x\).

Запомни, между целой и дробной частями можно поставить знак плюс, вот так: \( \displaystyle 5\frac<2><3>=5+\frac<2><3>\).

Так же можно проделать и обратное действие, т.е. преобразование из смешанной дроби в неправильную дробь.

Ты же знаешь, как это сделать?

Преобразование из смешанной дроби в неправильную дробь.

В результате получим исходное \( \displaystyle 17/3\).

Деление смешанных чисел: правило, примеры

В этой статье мы рассмотрим правило, по которому выполняется деление смешанных чисел. Как делить смешанные числа? Как разделить целое число на смешанную дробь? Как делить целое число на смешанную дробь и как смешанную дробь разделить на целое число? Ответы на эти вопросы вы будете знать после прочтения материала.

Деление смешанного числа на смешанное число

Деление смешанного числа на смешанное число удобнее всего свести к делению обыкновенных дробей. Как выглядит правило деления смешанных чисел? Сформулируем его.

Правило деления смешанных чисел

Чтобы разделить смешанное число на смешанное число, нужно:

Перейдем к примеру и разберем ход его решения.

Пример 1. Деление смешанного числа на смешанное число

После перевода смешанных чисел в неправильные дроби, получаем:

1 1 35 = 1 · 35 + 1 35 = 36 35

3 6 7 = 3 · 7 + 6 7 = 27 7

Теперь делим обыкновенные дроби и сокращаем результат:

На этом деление смешанных чисел окончено.

Деление смешанного числа на натуральное число

Пример 2. Деление смешанного числа на натуральное число

Переходим от смешанного числа к обыкновенной неправильной дроби:

3 3 4 = 3 · 4 + 3 4 = 15 4

Осуществляем деление и сокращаем:

3 3 4 ÷ 75 = 15 4 ÷ 75 = 15 4 · 75 = 1 20

На этом деление смешанного числа на натуральное число окончено.

Деление натурального числа на смешанное число

Как и в предыдущем пункте, такое деление сводится к переводу смешанного числа в обыкновенную дробь.

Единственное отличие состоит в том, что раньше мы переводили в вид обыкновенной дроби делимое, а теперь будем обращать делитель.

Пример 3. Деление натурального числа на смешанное число

Переведем делимое в вид обыкновенной дроби:

8 3 10 = 8 · 10 + 3 10 = 83 10

Теперь выполняем деление:

Данная неправильная дробь несократима. Для удобства, можно перевести ее обратно в смешанное число

Это и есть результат деления.

Деление смешанного числа на обыкновенную дробь

Как и все предыдущие случаи, деление смешанного числа на обыкновенную дробь также сводится к делению обыкновенных дробей. В любой непонятной ситуации переводите смешанное число в обыкновенную дробь!

Пример 4. Деление натурального числа на смешанное число

Переводим делимое также в вид обыкновенной дроби:

Делим, сокращаем и получаем ответ:

98 45 ÷ 28 15 = 98 45 · 15 28 = 98 3 · 28 = 98 84 = 7 6 = 1 1 6

Изучение основных правил умножения: как из неправильной дроби сделать правильную

Огромный блок математики посвящен работе с дробями или нецелыми числами. С ними очень часто встречаются и в жизни, поэтому знать, как работать с такими цифрами важно для любого человека. Математика – это наука, в которой ученик начинает с познания простых вещей и действий, а затем переходит к более сложным….

Знание и умение работать с подобными цифрами облегчит ему в дальнейшем работу с логарифмами, рациональными показателями и интегралами. С такими числами можно делать все то же самое, что и с обыкновенными: складывать дроби, делить, вычитать и умножать. Кроме этого, их можно сокращать. Работать с дробями просто, главное – это знать основные правила и методы их вычисления.

Основные понятия

Для того, чтобы понять, что это за значение такое, необходимо представить некий целый предмет. Допустим, что есть торт, который порезали на несколько одинаковых или равных кусков. Каждый кусочек будет называться долей.

Важно! В случае с дробями, есть некое целое число, которое состоит из равных долей – отдельных меньших чисел.

Например, 10 состоит из 5 двоек, каждая двойка – это часть от десяти.

Доли имеют свои названия, в зависимости от их общего количества в целом числе: 10 может состоять из двух пятёрок или пяти двоек, в первом случае она будет называться (одна вторая) , а во втором (одна пятая). Следует помнить, что равняется половине числа, (одна третья) трети, а (одна четвертая) – четвертью. Их могут также изображать через черточку: ½, 1/3 или 1/5.

Цифру, написанную сверху горизонтальной линии или слева от наклонной, называют числителем – он показывает сколько долей взяли у целого числа, а цифра под линии или справа от нее – знаменатель, он показывает на сколько всего долей разделили. Например, торт разделили на 10 кусков и сразу отложили два из них для опоздавших гостей. Это будет 2/10 (две десятых), т.е. взяли 2 (числитель) куска от общих 10 (знаменатель).

Дроби

Какие бывают доли, что такое неправильная дробь, что такое обыкновенная дробь? На эти вопросы легко ответить:

Смешанная цифра всегда может трансформироваться в неправильную дробь и наоборот.

Главное свойство гласит: при умножении, а также деления делимого и делителя на одинаковый множитель, в целом величина дроби не изменится. Это свойство делает возможным все операции с дробями.

Как из неправильной дроби сделать правильную

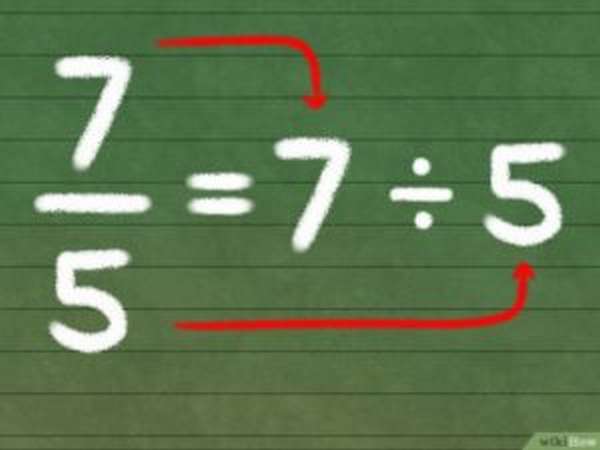
Это интересно! Изучаем математику в игровой форме: как ребенку быстро выучить таблицу умножения

Как сократить?

Главное правило гласит, что долевую цифру можно сократить поделить ее числитель и знаменатель на одинаковый делитель (отличный от 0) так, чтобы получилась новая цифра с меньшими параметрами, но равная исходной по величине. Исходя из этого правила можно понять, что дроби бывают сократимые и несократимые.

Сокращать можно при умножении дробных выражений друг на друга: * . Сами по себе эти числа несократимые, но выполняя операцию умножения, можно сократить их по диагонали: * = = . Сокращать при умножении можно только крест-накрест: числитель первой со знаменателем второй, и наоборот.

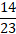
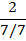
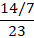
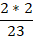
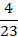
Сокращать можно и смешанную цифру, т.е. целую часть и правильную дробь представить в виде неправильной. Для этого следует выполнить некоторые действия:

Справедливо и обратное действие: из неправильной дроби сделать смешанную. Для этого рассмотрим обратное действие с :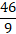

Таким способом сокращать дроби при любых операциях возможно. Можно сокращать значения ее делимого и делителя при умножении их на одинаковый множитель, и превращая из смешанного числа в долю, и наоборот.

Сокращение дробей

Возможные действия

Все основные виды вычислений доступны при счете долей, как и с целыми цифрами: сложение, вычитание и прочие. Рассмотрим каждое действие по отдельности с примерами:

Сложение и вычитание

Складывать доли можно двумя путями, в зависимости от их делителя. Они бывают одинаковыми и разными. Рассмотрим пример складывания долей с одинаковыми делителями.

Для решения + необходимо по отдельности сложить делимое долей, а делитель не трогать: 1+1. Результатом станет цифра , но поскольку она неправильная, то ее можно преобразовать в смешанную, разделив делимое на делитель: 2:2= 1. Неправильную долю всегда (!) следует приводить к правильной и несокращаемой, т. е. если ее делимое и делитель можно поделить на одинаковый множитель – это следует сделать в обязательно порядке.

В случае сложения долей с различными делителями, их необходимо изначально привести к одинаковому. Например, для решения : 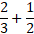необходимо:

Вычитание осуществляется точно так же: в случае с одинаковыми делителями их не трогаем, а числители последовательно вычитаем: = = . Если же знаменатели различные, то следует поступить, как и при сложении: найти НОК, множители, умножить доли, а затем вычесть уже доли с одинаковыми делителями.

Сложение дробей

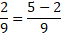
Умножение и деление

При умножении необходимо последовательно перемножить их верх и низ между собой: 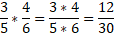= поскольку есть возможность сокращения на 6. В случае деления все несколько сложнее.

Для деления 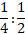следует:

Важно! Деление всегда можно заменить умножением, но только при соблюдении условия замены делителя на обратное ему число.

Перевод смешанного числа в неправильную дробь

Выделение целой части из неправильной дроби

Чтобы правильно решать подобные примеры, следует запомнить главное свойство и правила сокращения. Что касается операций, то важно знать, как правильно складывать и умножать при одинаковых и разных знаменателях, поскольку делятся и вычитаются они по одинаковому принципу.

Математика. 5 класс

Конспект урока

Понятие смешанной дроби

Перечень рассматриваемых вопросов:

– введение понятий «смешанная дробь», «целая часть смешанной дроби», «дробная часть смешанной дроби»;

– правило преобразования неправильных дробей в смешанные дроби;

– правило преобразования смешанных дробей в неправильные дроби;

– отработка правил преобразования неправильных и смешанных дробей;

– сравнение смешанных дробей.

Правильная дробь – дробь, числитель которой меньше знаменателя.

Неправильная дробь – дробь, числитель которой больше знаменателя.

Смешанная дробь – сумма натурального числа и правильной дроби, записанная без знака плюс;

Целая часть смешанной дроби – натуральное число в смешанной дроби.

Дробная часть смешанной дроби – правильная дробь в смешанной дроби.

Теоретический материал для самостоятельного изучения

Вы уже знакомы с обыкновенными дробями. Умеете выполнять с ними все арифметические действия. Знаете, что обыкновенные дроби бывают правильными – это те дроби, числитель которых меньше знаменателя, и неправильными – дроби, у которых числитель больше знаменателя.

Если числитель неправильной дроби делится на знаменатель без остатка, то такая неправильная дробь равна частному от деления числителя на знаменатель.

Сумму натурального числа три и правильной дроби две пятых, записанную сокращённо, без знака плюс, называют смешанной дробью.

Натуральное число «три» в смешанной дроби «три целых две пятых» называют целой частью, а правильную дробь «две пятых» – дробной частью смешанной дроби.

Чтобы правильно назвать дробную часть смешанной дроби поступаем так: называя числитель, отвечаем на вопрос: «сколько долей взято?» – две. Называя знаменатель, отвечаем на вопрос: «две каких?» – пятых.

Научимся записывать неправильные дроби, числитель которых не делится на знаменатель нацело, в виде смешанных дробей.

Каждую смешанную дробь можно представить в виде неправильной дроби.

• знаменатель дробной части умножить на целую часть,

• прибавить к этому числу числитель дробной части,

• полученное число записать в числитель искомой неправильной дроби,

• знаменатель оставить прежним.

Так как у этих дробей целые части одинаковые, то сравнивать мы будем дробные части. Но дробные части данных дробей имеют разные знаменатели. Чтобы сравнить дроби с разным знаменателем, нужно привести их сначала к общему знаменателю. Меньшей из них будет та дробь, числитель которой меньше.

А можно ли сравнить эти дроби, не приводя их к общему знаменателю? Можно. И даже не одним способом.

Преобразуем каждую смешанную дробь в неправильную, пользуясь правилом:

– знаменатель умножить на целую часть,

– прибавить его к дробной части,

– полученное число записать в числитель,

– знаменатель останется прежним.

Для того чтобы выбрать равные дроби, нужно привести их к одинаковому виду: или все дроби сделать неправильными, или все дроби – смешанными.

Преобразуем первые четыре неправильные дроби в смешанные числа.

Как из смешанной дроби сделать обыкновенную?

Как из смешанной дроби сделать обыкновенную?

Ответьте срочно надо.

Нужно знаменатель умножить на целую часть и прибавить числитель.

Срочно?

Установите, прилагательные каких разрядов употреблены в данных словосочетании.

Прослонять по падежам?

Прослонять по падежам.

Обыкновенную дробь семь восьмых и полторы минуты.

Запишите обыкновенную дробь в виде десятичной?

Запишите обыкновенную дробь в виде десятичной.

Вычислите 20 балов.

Срочно ответьти прошу?

Срочно ответьти прошу.

Замени и ты слова обыкновенными дробями и запеши их на бланке ответов.

Сделать морфологический разбор слова «смешанного»?

Сделать морфологический разбор слова «смешанного».

Очень срочно ответьте?

Очень срочно ответьте.

Неопределенный дробь в смешанную дробь 10 / 7, 15 / 6, 12 / 10?

Неопределенный дробь в смешанную дробь 10 / 7, 15 / 6, 12 / 10.

Слитно или раздельно (не)обыкновенное?

Слитно или раздельно (не)обыкновенное?

Набережная существительное одной чертой(какая) красивая двумя чертами Около подчеркиваем волнистой линией в. В сл моря одна черта существительное Время дня одной чертой сущ какое жаркое двумя чертами ветвями какими большими.

А) парочку Б) дразнится В) стишок.

1 схема. Солнце светит. Повествовательное. 2 схема. Девочка делает зарядку. Повествовательное. 3 схема. С дерева упало сочное яблоко. Повествовательное. 4схема. Мальчик думает о маме и о папе. Повествовательное. 5схема. Крпсивый лебедь п..

1. Звуки речи 2. Сами звуки 1. Песня 2. Басня 3. Конец.

ПрЕломление ПрЕподнести ПрЕкратить споры ПрЕстиж ПрЕзумция ПрЕмьера ПрЕвратно понятый ПрЕсимпатичный ПрЕсимпатичный.

Решение в приложении Всё остальное у Вас правильно.

Источники информации:

• http://www.for6cl.uznateshe.ru/kak-smeshannoe-chislo-perevesti-v-nepravilnuyu-drob/
• http://obrazavr.ru/matematika/5-klass-matematika/desyatichnye-drobi/delenie-desyatichnyh-drobej/perevod-periodicheskoj-drobi-v-obyknovennuyu-drob/
• http://intmag24.ru/dlya-shkolnikov/drobi/
• http://xn—-8sbanwvcjzh9e.xn--p1ai/raznoe/kak-perevesti-obyknovennuyu-drob-v-nepravilnuyu-drob-v-kak-preobrazovat-smeshannuyu-v-nepravilnuyu-drob.html
• http://youclever.org/book/drobi/
• http://zaochnik.com/spravochnik/matematika/dejstvitelnye-ratsionalnye-irratsionalnye-chisla/delenie-smeshannyh-chisel/
• http://tvercult.ru/nauka/izuchenie-osnovnyih-pravil-umnozheniya-kak-iz-nepravilnoy-drobi-sdelat-pravilnuyu
• http://resh.edu.ru/subject/lesson/7761/conspect/
• http://russkij-azyk.my-dict.ru/q/388823_kak-iz-smesannoj-drobi-sdelat-obyknovennuu/