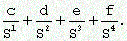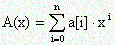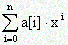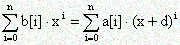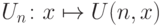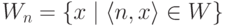функция f с натуральными аргументами и значениями определена так
Функция f с натуральными аргументами и значениями определена так
Дано число а и натуральное число n.
Вычислить а n (a в степени n).
Другое решение этой задачи:
Число выполняемых операторов присваивания равно n.
За каждые два вхождения в цикл значение переменной k уменьшается по крайней мере вдвое. В цикле выполняется 2 операции присваивания. Поэтому общее число действий не превосходит 4·log2 n.
Дано натуральное число n, вычислить n! (1!=1, n!=n((n-1)!).
Дано натуральное n, вычислить 1/1!+. +1/n! так, чтобы число операций (выполняемых команд присваивания) было бы порядка n (не более C·n для некоторой константы С).
Важно не вычислять заново каждый раз n!.
n!=1·2·3·. ·(n-1)·n=(n-1)!·n. В нашем примере 1/n!=1/((n-1)!·n), т.е. каждый j элемент получается делением (j-1)-го элемента на j.
Число выполняемых операций присваивания равно 3·n.
Алгоритм Евклида. Будем считать, что
(см. Основы информатики и вычислительной техники, часть 1, под ред. А.П. Ершова и В.М. Монахова или А.Г. Кушниренко и др. Основы информатики и вычислительной техники)
while not ((m=0) or (n=0)) do
if m>=n then m:=m-n else n:=n-m;
if m=0 then d:=n else d:=m;
Даны два натуральных числа а и b, не равные нулю одновременно. Найти d=НОД(а,b) и такие x и y, что d=a·x+b·y.
Добавим переменные p,q,r,s такие, что m=p·a+q·b, n=r·a+s·b.
while not ((m=0) or (n=0)) do
Даны натуральные числа n и k, n>1. Напечатать k десятичных знаков числа 1/n. Программа должна использовать только целые переменные.
Сдвинув в десятичной записи числа 1/n запятую на k мест вправо, получим число (10 k )/n. Нам надо напечатать его целую часть, то есть разделить 10 k на n нацело. Стандартный способ требует использования больших по величине чисел, которые могут выйти за границы диапазона представимых чисел.
Воспользуемся методом «деления уголком» и будем хранить «остаток» r.
Функция f с натуральными аргументами и значениями определена так: f(0)=0, f(1)=1, f(2n)=f(n), f(2n+1)=f(n)+f(n+1). Составить программу вычисления f(n) по заданному n, требующую порядка log2 n операций (не более C·log2 n).
Функцию f можно записать в общем виде: f(n)=a(f(k)+b(f(k+1).
Для k=2m: f(k)=f(m), f(k+1)=f(2m+1)=f(m)+f(m+1). Тогда
then begin m:=k div 2; a:=a+b; k:=m; end
else begin m:=k div 2; b:=a+b; k:=m; end;
При каждом вхождении в цикл значение переменной k уменьшается вдвое.
Поэтому число операций не более 3·log2 n.
Дано n. Вычислить an. Число операций должно быть порядка log2 n.
2. Написать вариант алгоритма Евклида, использующий соотношения
НОД(2a,b)=НОД(a,b) при нечетном b, использующий лишь деление на 2 и проверку четности. Число действий должно быть порядка log2 n для исходных данных, не превосходящих n.
3. Функция f определена так: f(0)=13, f(1)=17, f(2n+1)=43f(n)+57f(n+1),
Функция f с натуральными аргументами и значениями определена так
Число вводится своим двоичным представлением (длина числа не превышает 10000 двоичных разрядов). Необходимо определить делится ли число на 15.
Дано число в K-ичной системе счисления
при условии, что 0 0.
Рассмотрим систему счисления с двумя цифрами 0 и 1, в которой, в отличие от двоичной системы весами являются не степени двойки 1,2,4,8,16. а числа Фибоначчи 1,2,3,5,8,13. В этой системе счисления каждое положительное целое число единственным образом представляется в виде строки нулей и единиц, которая начинается с 1 и в которой нет двух единиц, стоящих рядом.
Даны две строки, представляющие числа A и B. Найти строку, представляющую число A+B.
Пример. Исходные строки ‘10101’ и ‘100’ представляют числа 8+3+1=12 и 3. Ответом является строка ‘100010’, представляющая строку 13+2=15=12+3.
Примечание. Строки могут быть столь длинны, что числа A и B превысят максимально допустимое в вашем компьютере целое число.
Сосчитать количество единиц в двоичной записи числа i.
Последовательность 011212201220200112. строится так: сначала пишется 0, затем повторяется следующее действие: уже написанную часть приписывают справа с заменой 0 на 1, 1 на 2, 2 на 0, т.е.
Составить алгоритм, который по введенному N, (0
Дан массив X(100) и Y(100). Записать алгоритм, меняющий последовательно местами значения элементов X(k) и Y(k) для этих таблиц, для k=1,2. 100, не используя промежуточных переменных.
Точки с целочисленными координатами из 1-го квадранта помечаются числами 0,1,2. слева направо и снизу вверх таким образом, что очередной точке приписывается минимальное число, отсутствующее в вертикали и горизонтали, проходящей через точку. Первой помечается точка (0,0).
Написать программу, которая
1. По заданным координатам x и y, x>=0, y>=0, x,y- целые, определяет пометку точки.
Известно, что запись числа A в позиционных системах счисления с основанием p и q имеет вид бесконечной периодической дроби с периодом 2:
Написать программу, которая для введенных натуральных чисел p и q (2 q) находит и выводит все возможные пары значений цифр a и b, удовлетворяющих соотношению (*). Если таковых нет, вывести сообщение ‘Пригодных цифр нет’.
Предусмотреть защиту от ввода ошибочных данных.
Вводятся 3 целых числа n,a,b.
Необходимо определить, принадлежит ли точка с координатой a/b множеству K[n].
Дано натуральное n. Подсчитать количество решений неравенства x*x + y*y 1/2 )
Число называется совершенным, если оно равно сумме всех своих делителей за исключением его самого. Любое четное совершенное число представимо в виде
Найти двоичное представление для максимального совершенного четного числа меньшего введенного N.
Заданы натуральные числа E,K,M,T в записи химической реакции
Какую минимальную площадь может иметь треугольник ABC?
Функция f с натуральными аргументами и значениями определена так: f(0)=0, f(1)=1, f(2n)=f(n), f(2n+1) = f(n) + f(n+1). Составить программу вычисления f (n) по заданному n, требующую порядка log n операций
Определить количество повторений каждой из цифр 0,1,2. 9 в числе N N (N в степени N), N
Вводится N. Необходимо найти, на сколько нулей оканчивается N!=1*2*3*. *N.
Натуральное число N>1 представить в виде суммы натуральных чисел так, чтобы произведение этих слагаемых было максимально.
Даны целые числа А(0),А(1). А(5). Найти множество корней уравнения
Вывести в порядке возрастания все обыкновенные несократимые дроби, заключенные между 0 и 1, знаменатели которых не превышают 15. Массив при этом заводить не следует.
Найти это значение.
Полином N-ой степени
задается своими коэффициентами a[i]. Найти коэффициенты b[i],i=0. n*m, m-ой степени полинома A(x). Числа n,m
P(x) =x n + A[1]*x n-1 +. + A[N-1]*x + A[N]
задается набором своих коэффициентов a[i], i=0. n. Необходимо вычислить коэффициенты b[i] такого многочлена, что
Вычислить значение полинома
f(x)=ax 4 +bx 3 +cx 2 +dx+e
Вычислимость, разрешимость и перечислимость
Перечислимые и разрешимые множества
Теорема 2. Всякое разрешимое множество натуральных чисел перечислимо. Если множество A и его дополнение (до множества всех натуральных чисел) перечислимы, то A разрешимо.
Этот факт называют теоремой Поста
Она говорит, что разрешимые множества это перечислимые множества с перечислимыми дополнениями. Напротив, перечислимые множества можно определить через разрешимые:
Теорема 3. Множество P натуральных чисел перечислимо тогда и только тогда, когда оно является проекцией некоторого разрешимого множества Q пар натуральных чисел. ( Проекция получается, если от пар оставить их первые компоненты: 
.)
Проекция любого перечислимого множества перечислима (перечисляющий алгоритм должен лишь удалять вторые члены пар), так что проекция разрешимого множества тем более перечислима.
Перечислимость и вычислимость
Мы видели, что перечислимое множество можно определить в терминах вычислимых функций (например, как область определения вычислимой функции). Можно сделать и наоборот:
Теорема 4. Функция f с натуральными аргументами и значениями вычислима тогда и только тогда, когда ее график
является перечислимым множеством пар натуральных чисел.
Теорема 5. Прообраз и образ перечислимого множества при вычислимой функции перечислимы.
Дальнейшие свойства вычислимых действительных чисел см. в задаче 23.
Построение графиков функций
Понятие функции
Функция — это зависимость y от x, где x является переменной или аргументом функции, а y — зависимой переменной или значением функции.
Задать функцию значит определить правило, в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:
Область определения — множество х, то есть область допустимых значений выражения, которое записано в формуле.
Например, для функции вида 
область определения выглядит так
Область значений — множество у, то есть это значения, которые может принимать функция.
Например, естественная область значений функции y = x² — это все числа больше либо равные нулю. Можно записать вот так: Е (у): у ≥ 0.
Понятие графика функции
Графиком функции y = f(x) называется множество точек (x; y), координаты которых связаны соотношением y = f(x). Само равенство y = f(x) называется уравнением данного графика.
График функции — это множество точек (x; y), где x — это аргумент, а y — значение функции, которое соответствует данному аргументу.
Проще говоря, график функции показывает множество всех точек, координаты которых можно найти, просто подставив в функцию любые числа вместо x.
Для примера возьмём самую простую функцию, в которой аргумент равен значению функции, то есть y = x.
В этом случае нам не придётся вычислять для каждого аргумента значение функции, так как они равны, поэтому у всех точек нашего графика абсцисса будет равна ординате.
Если мы последовательно от наименьшего значения аргумента к большему соединим отмеченные точки, то у нас получится прямая линия. Значит графиком функции y = x является прямая. На графике это выглядит так:
Надпись на чертеже y = x — это уравнение графика. Ставить надпись с уравнением на чертеже удобно, чтобы не запутаться в решении задач.
Важно отметить, что прямая линия бесконечна в обе стороны. Хоть мы и называем часть прямой графиком функции, на самом деле на чертеже изображена только малая часть графика.
Исследование функции
Важные точки графика функции y = f(x):
Стационарные точки — точки, в которых производная функции f(x) равна нулю.
Критические точки — точки, в которых производная функции f(x) равна нулю либо не существует. Стационарные точки являются подмножеством множества критических точек.
Экстремум в математике — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума.
Нули функции — это значения аргумента, при которых функция равна нулю.
Асимптота — прямая, которая обладает таким свойством, что расстояние от точки графика функции до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат. По способам их отыскания выделяют три вида асимптот: вертикальные, горизонтальные, наклонные.
Функция непрерывна в точке k, если предел функции в данной точке равен значению функции в этой точке: 
Если функция f(x) не является непрерывной в точке x = a, то говорят, что f(x) имеет разрыв в этой точке.
Если нам нужно построить график незнакомой функции, когда заранее невозможно представить вид графика, полезно применять схему исследования свойств функции. Она поможет составить представление о графике и приступить к построению по точкам.
Схема построения графика функции:
У нас есть отличные онлайн занятия по математике для учеников с 1 по 11 классы! Приходи на пробное занятие с нашими лучшими преподавателями!
Построение графика функции
Чтобы понять, как строить графики функций, потренируемся на примерах.
Задача 1. Построим график функции 
Упростим формулу функции:
Задача 2. Построим график функции
Выделим в формуле функции целую часть:
График функции — гипербола, сдвинутая на 3 вправо по x и на 2 вверх по y и растянутая в 10 раз по сравнению с графиком функции 
Выделение целой части — полезный прием, который применяется в решении неравенств, построении графиков и оценке целых величин.
Задача 3. По виду графика определить знаки коэффициентов общего вида функции y = ax2 + bx + c.
Вспомним, как параметры a, b и c определяют положение параболы.
Ветви вниз, следовательно, a 0.
Точка пересечения с осью Oy — c = 0.
Координата вершины 
, т.к. неизвестное число при делении на положительное дает отрицательный результат, то это число отрицательное, следовательно, b > 0.
Ветви вниз, следовательно, a 0.
Координата вершины 
, т.к. неизвестное число при делении на отрицательное дает в результате положительное, то это число отрицательное, следовательно, b
| x | y |
| 0 | -1 |
| 1 | 2 |
| x | y |
| 0 | 2 |
| 1 | 1 |
| x | y |
| 0 | 0 |
| 1 | 2 |
k = 2 > 0 — угол наклона к оси Ox острый, B = 0 — график проходит через начало координат.
Задача 5. Построить график функции 
Это дробно-рациональная функция. Область определения функции D(y): x ≠ 4; x ≠ 0.
Нули функции: 3, 2, 6.
Промежутки знакопостоянства функции определим с помощью метода интервалов.
Вертикальные асимптоты: x = 0, x = 4.
Если x стремится к бесконечности, то у стремится к 1. Значит, y = 1 — горизонтальная асимптота.
Вот так выглядит график:
Задача 6. Построить графики функций:
б) 
г) 
д) 
Когда сложная функция получена из простейшей через несколько преобразований, то преобразования графиков можно выполнить в порядке арифметических действий с аргументом.
а) 
Преобразование в одно действие типа f(x) + a.
Сдвигаем график вверх на 1:
б)
Сдвигаем график вправо на 1:
Сдвигаем график вправо на 1:
Сдвигаем график вверх на 2:
г) 
Преобразование в одно действие типа 
Растягиваем график в 2 раза от оси ординат вдоль оси абсцисс:
д) 
Чтобы выполнить преобразования, посмотрим на порядок действий: сначала умножаем, затем складываем, а уже потом меняем знак. Чтобы применить умножение ко всему аргументу модуля в целом, вынесем двойку за скобки в модуле.
Сжимаем график в два раза вдоль оси абсцисс:
Сдвигаем график влево на 1/2 вдоль оси абсцисс:
Отражаем график симметрично относительно оси абсцисс:
Универсальные функции и неразрешимость
Универсальные функции
Говорят, что функция U двух натуральных аргументов является универсальной для класса вычислимых функций одного аргумента, если для каждого n функция
Аналогичное определение можно дать и для других классов функций (одного аргумента): например, функция U двух аргументов будет универсальной для класса всех всюду определенных вычислимых функций одного аргумента, если ее сечения Un являются всюду определенными вычислимыми функциями одного аргумента и исчерпывают все такие функции. Очевидно, универсальные функции существуют для любых счетных классов (и только для них).
Ключевую роль в этом разделе играет такой факт:
Теорема 6.Существует вычислимая функция двух аргументов, являющаяся универсальной функцией для класса вычислимых функций одного аргумента.
15. Все сечения Un некоторой функции U двух аргументов вычислимы. Следует ли отсюда, что функция U вычислима?
16. Дайте (естественное) определение понятия вычислимой функции трех аргументов, универсальной для класса вычислимых функций двух аргументов, и докажите ее существование.
Для множеств используется аналогичная терминология: множество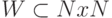 
называют универсальны для некоторого класса множеств натуральных чисел, если все сечения
множества W принадлежат этому классу и других множеств в классе нет.
Теорема 7.Существует перечислимое множество пар натуральных чисел, универсальное для класса всех перечислимых множеств натуральных чисел.
18. Существует ли разрешимое множество пар натуральных чисел, универсальное для класса всех разрешимых множеств натуральных чисел?
Диагональная конструкция
В предыдущем разделе мы построили универсальную функцию для класса всех вычислимых функций одного аргумента. Можно ли сделать то же самое для класса всюду определенных вычислимых функций? Оказывается, что нет.
Теорема 8.Не существует вычислимой всюду определенной функции двух аргументов, универсальной для класса всех вычислимых всюду определенных функций одного аргумента.
Тем не менее, часть рассуждения остается в силе.
19. Докажите, что и сама функция d из доказательства предыдущей теоремы не имеет вычислимого всюду определенного продолжения.