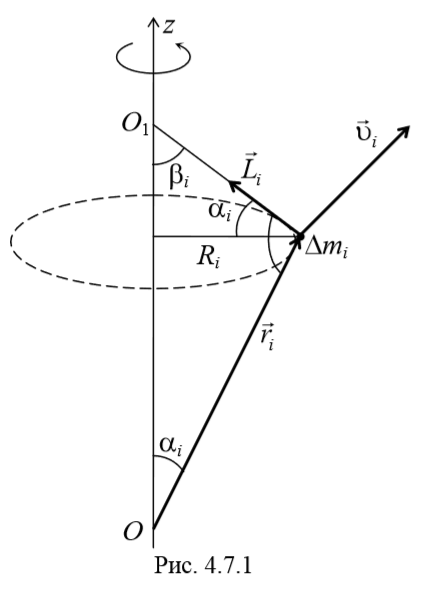
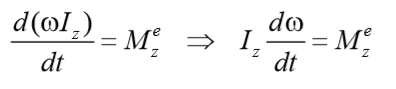
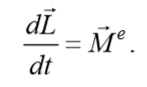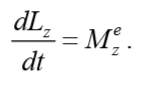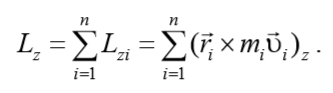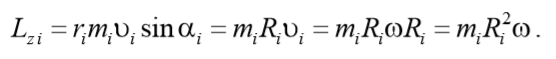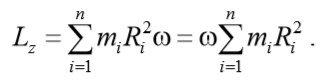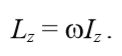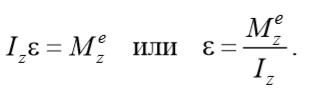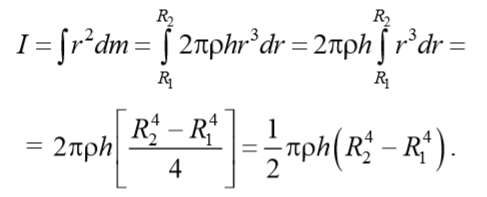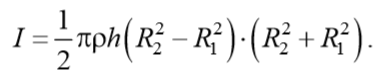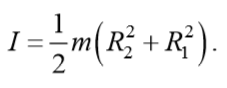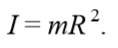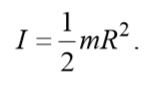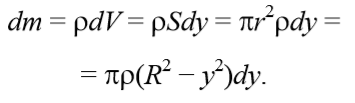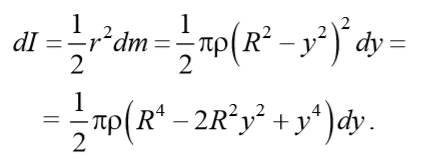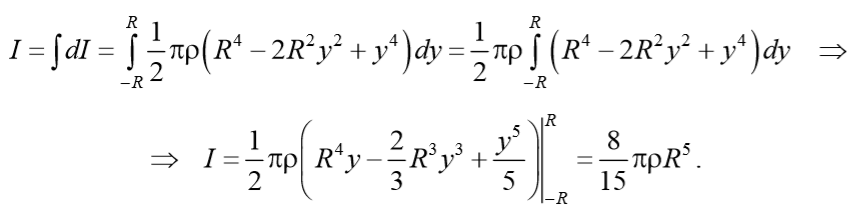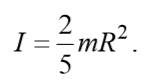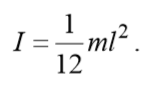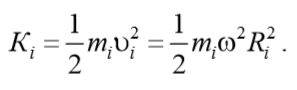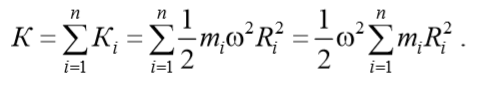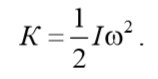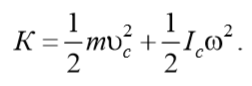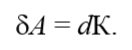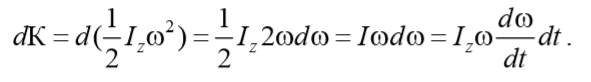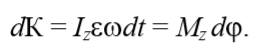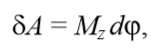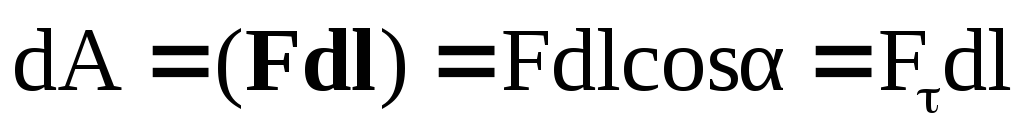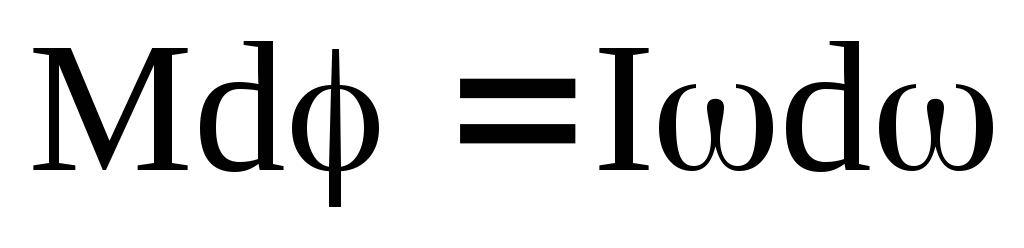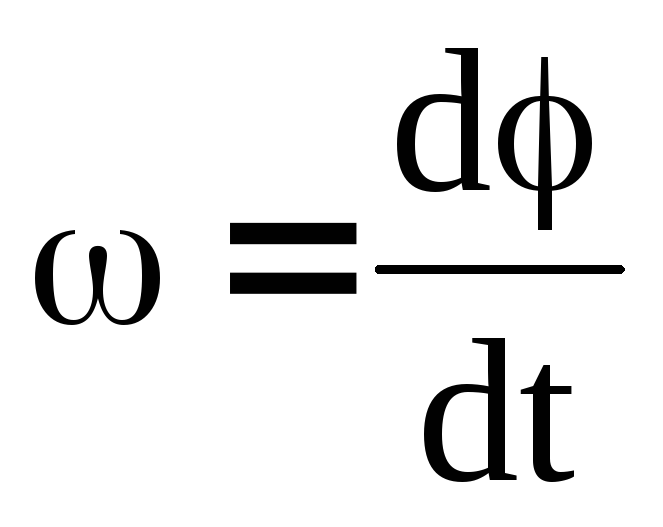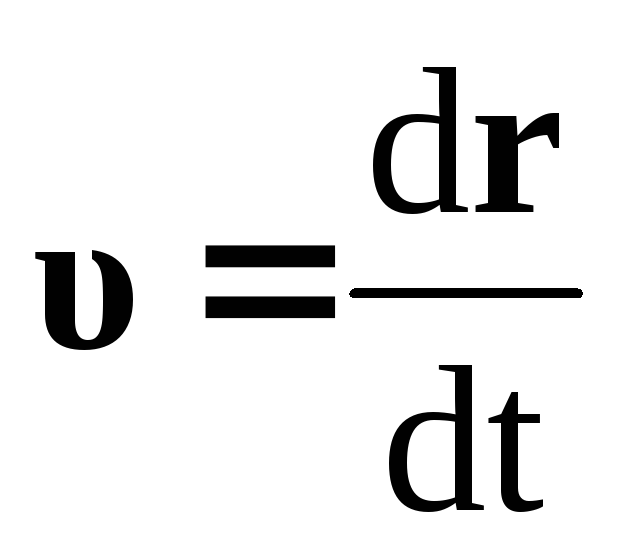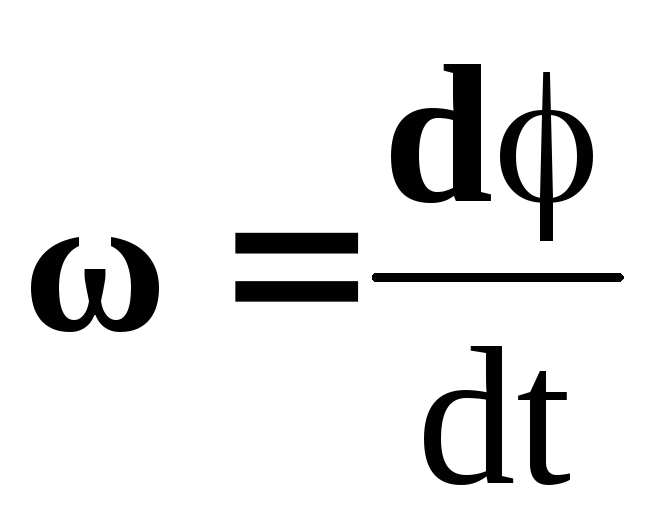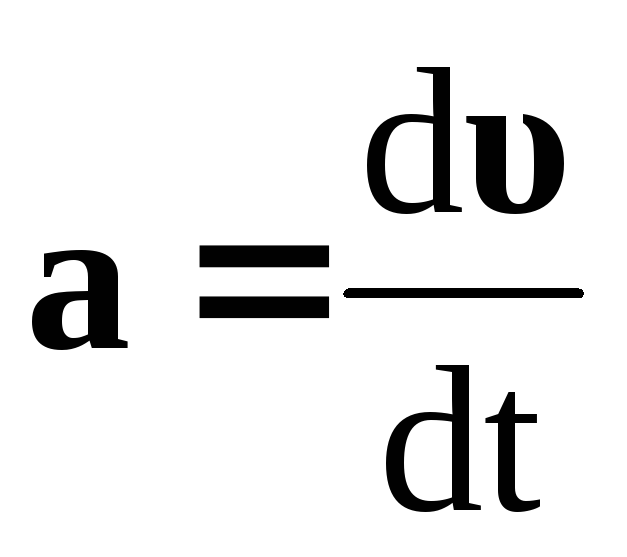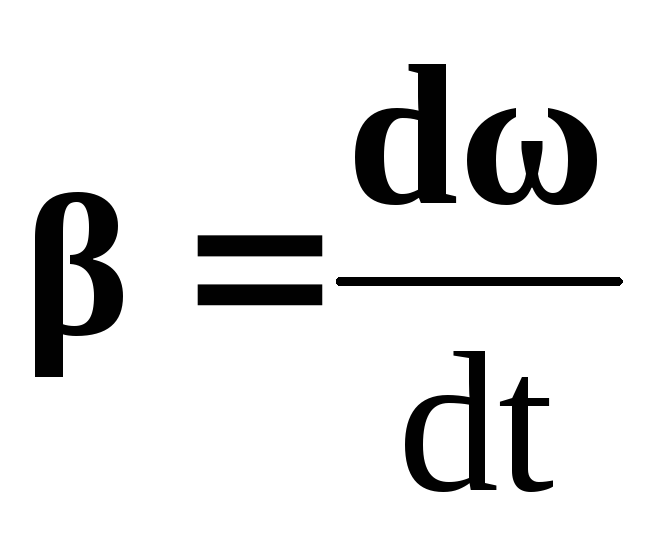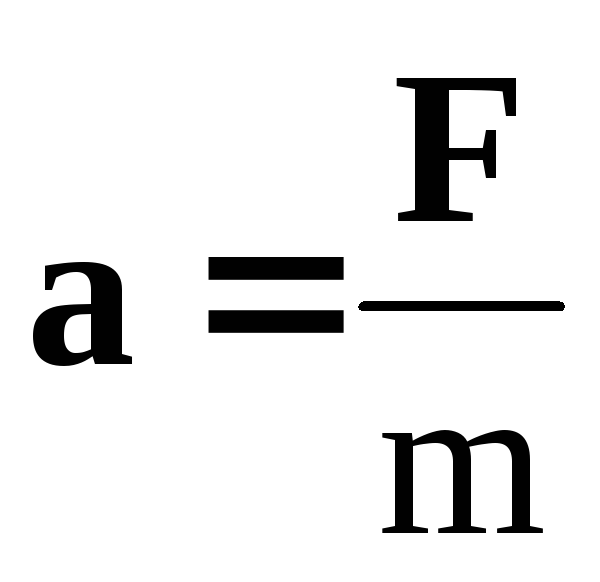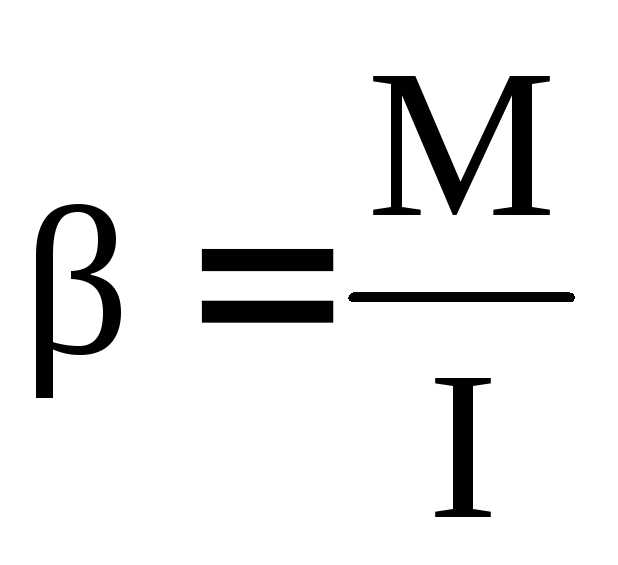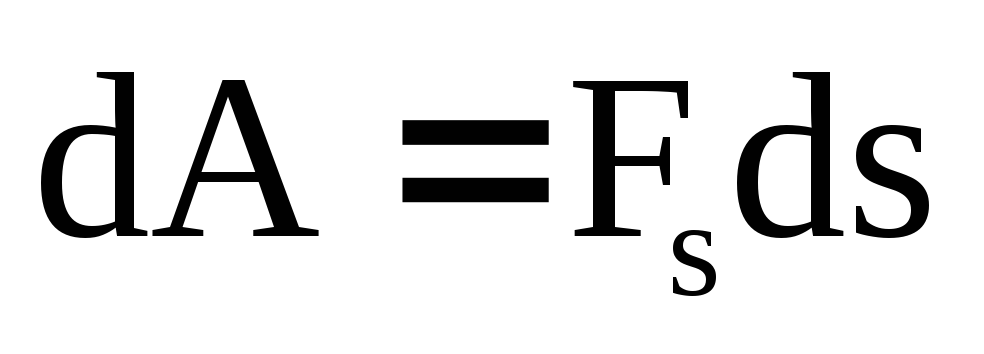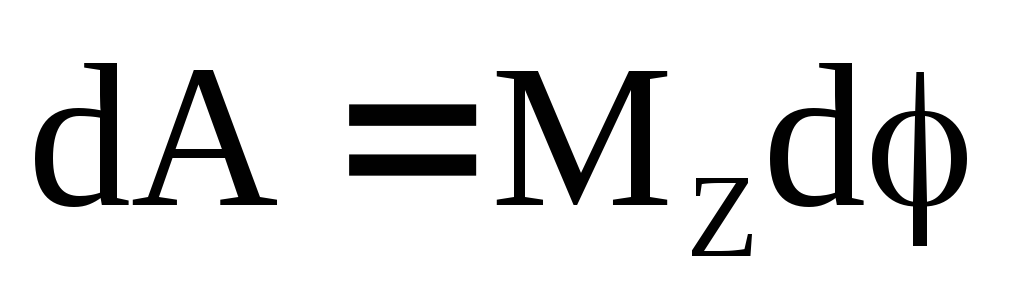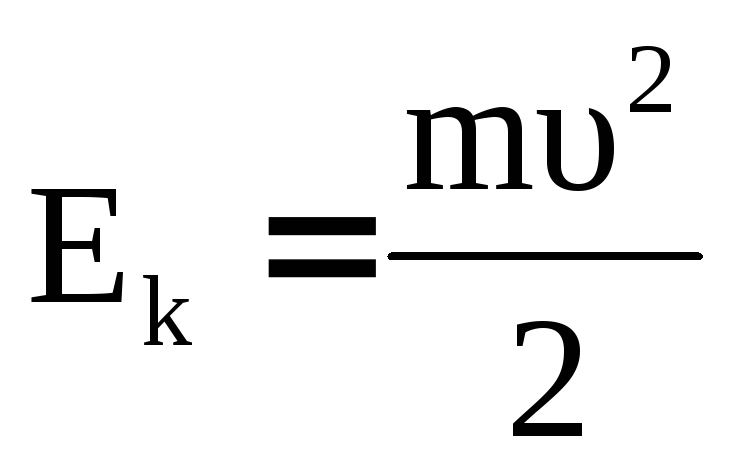уравнение динамики вращательного движения твердого тела относительно неподвижной оси z выглядит так

Физика Б1.Б8.

Электронное учебное пособие по разделу курса физики Механика

Механика – это раздел физики, который изучает наиболее простой вид движения материи – механическое движение и причины, вызывающие или изменяющие это движение.

Механика состоит из трех разделов: кинематики, динамики и статики. Кинематика дает математическое описание движения, не касаясь причин, которыми вызвано движение. Динамика – основной раздел механики, она изучает законы движения тел и причины, которыми вывзывается движение и его изменение. Статика изучает законы равновесия системы тел под действием приложенных сил. Мы ограничимся изучением двух основных разделов – кинематики и динамики.

Введение

Механика – это раздел физики, который изучает наиболее простой вид движения материи – механическое движение и причины, вызывающие или изменяющие это движение.

Механическое движение – это изменение во времени взаимного расположения тел или частей одного и того же тела. Причиной, вызывающей механическое движение тела или его изменение, является воздействие со стороны других тел.

Развитие механики началось еще в древние времена, однако, как наука она формировалась в средние века. Основные законы механики установлены итальянским физиком и астрономом Г. Галилеем (1564-1642) и английским ученым И. Ньютоном (1643-1727).

Механику Галилея-Ньютона принято называть классической механикой. В ней изучается движение макроскопических тел, скорости которых значительно меньше скорости света с в вакууме. Законы движения тел со скоростями, близкими к скорости света сформулированы А. Эйнштейном (1879-1955), они отличаются от законов классической механики. Теория Эйнштейна называется специальной теорией относительности и лежит в основе релятивистской механики. Законы классической механики неприемлемы к описанию движения микроскопических тел (элементарных частиц – электронов, протонов, нейтронов, атомных ядер, самих атомов и т.д.) их движение описывается законами квантовой механики.

Механика состоит из трех разделов: кинематики, динамики и статики. Кинематика дает математическое описание движения, не касаясь причин, которыми вызвано движение. Динамика – основной раздел механики, она изучает законы движения тел и причины, которыми вывзывается движение и его изменение. Статика изучает законы равновесия системы тел под действием приложенных сил. Мы ограничимся изучением двух основных разделов – кинематики и динамики.

В механике для описания движения в зависимости от условий решаемой задачи пользуются различными упрощающими моделями: материальная точка, абсолютно твердое тело, абсолютно упругое тело, абсолютно неупругое тело, и т.д. Выбор той или иной модели диктуется необходимостью учесть в задаче все существенные особенности реального движения и отбросить несущественные, усложняющие решение.

Материальная точка – это тело обладающее массой, размеры и форма которого несущественны в данной задаче. Любое твердое тело или систему тел можно рассматривать как систему материальных точек. Для этого любое тело или тела системы нужно мысленно разбить на большое число частей так, чтобы размеры каждой части были пренебрежимо малы по сравнению с размерами самих тел.

Абсолютно твердое тело – это тело, расстояние между любыми точками которого остается неизменным в процессе движения или взаимодействия. Эта модель пригодна, когда можно пренебречь деформацией тел в процессе движения.

Абсолютно упругое и абсолютно неупругое тело – это два предельных случая реальных тел, деформациями которых можно и нельзя пренебречь в изучаемых процессах.

Любое движение рассматривается в пространстве и времени. В пространстве определяется местоположение тела, во времени происходит смена местоположений или состояний тела в пространстве, время выражает длительность состояния движения или процесса. Пространство и время –это два фундаментальных понятия, без которых теряется смысл понятия движения: движения не может быть вне времени и пространства.

Источник

Лекция №6. ДИНАМИКА АБСОЛЮТНО ТВЕРДОГО ТЕЛА

4.7. Основное уравнение динамики вращательного движения относительно неподвижной оси.

Найдем проекции правой и левой части уравнения (4.7.1) на ось Oz :

Подставим правую часть уравнения (4.7.4) в (4.7.3)

Подставляя (4.7.6) в выражение (4.7.1)

Угловое ускорение при вращении твердого тела относительно неподвижной оси прямо пропорционально результирующему моменту внешних сил относительно этой оси и обратно пропорционально моменту инерции тела относительно этой же оси.

Физический смысл момента инерции можно определить из выражения (4.7.8). Если сравнить с основным уравнением динамики поступательного движения (2.1.2), то можно увидеть что роль массы при вращательном движении выполняет момент инерции. Момент инерции тела является мерой инерции тела при вращательном движении.

Если проекцию моментов внешних сил относительно оси z равна нулю, то момент импульса тела относительно этой оси с течением времени не будет изменяться.

4.8. Расчет моментов инерции.

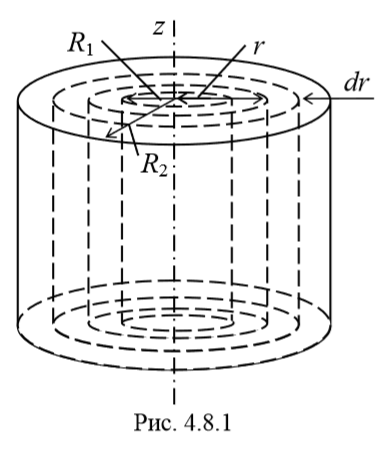
1) Момент инерции однородного полого цилиндра.

Таким образом, момент инерции получается посредством интегрирования по всем кольцам:

Таким образом, момент инерции полого цилиндра

Следовательно, момент инерции любого бесконечно малого цилиндра можно записать в виде:

Интегрируя по всем бесконечно малым цилиндрам, получим:

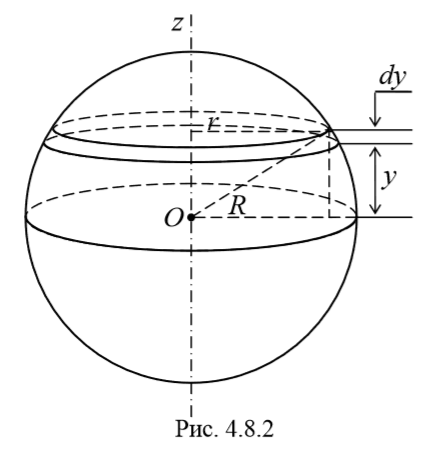
Таким образом, момент инерции шара будет равен

5) Момент инерции однородного стержня. Момент инерции стержня длиной l относительно оси проходящей через середину стержня перпендикулярно его длине:

4.9. Кинетическая энергия вращающегося тела.

Кинетическая энергия тела складывается из кинетических энергий его частей, т. е.

Кинетическая энергия тела при плоском движении слагается из энергии поступательного движения со скоростью, равной скорости центра масс, и энергии вращения вокруг оси, проходящей через центр масс тела, т. е.

4.10. Работа силы при вращении тела.

Работа, совершаемая всеми приложенными к телу силами, идет на изменение его кинетической энергии:

Подставим в последнее выражение уравнение (4.9.3) и продифференцируем

Тогда элементарная работа, совершаемая силами, приложенными к телу

и полная работа при повороте тела на угол φ за время t

Источник

Уравнение динамики вращательного движения твердого тела вокруг неподвижной оси

Для вывода уравнения динамики вращательного движения твердого тела используем теорему о кинетической энергии: работа результирующей всех сил, действующих на тело, идет на приращение кинетической энергии: dA=dE_k.

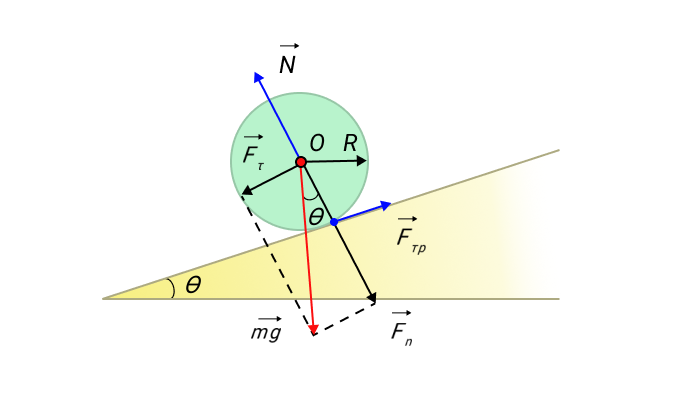
Пусть к телу, закрепленному на оси О, в горизонтальной плоскости приложена внешняя сила F (рис.5).

Напомним, что элементарной работой dA силы F называется скалярное произведение силы F на бесконечно малое перемещение dl:

Отметим, что нормальная составляющая силы F_n (в отличие от тангенциальной F_τ) и сила реакции опоры N работы не совершают, так как они перпендикулярны направлению перемещения.

Элемент dl=rd при небольших углах поворота d (r – радиус-вектор элемента тела). Тогда работа этой силы записывается следующим образом:

. (19)

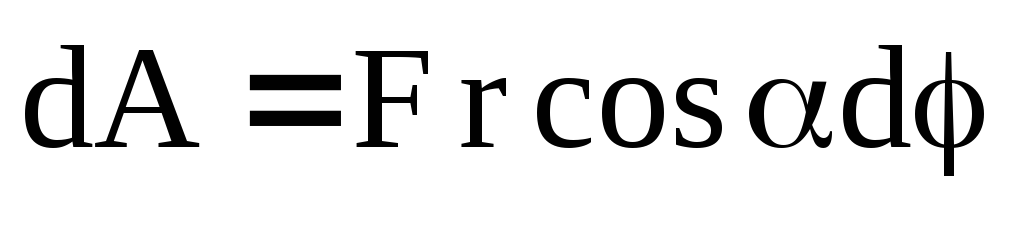
Выражение Fr cos является моментом силы (произведение силы F на плечо p=r cos):

(20)

Тогда работа равна

. (21)

Эта работа затрачивается на изменение кинетической энергии вращения:

. (22)

Если I=const, то после дифференцирования правой части получим:

или, так как

, (23)

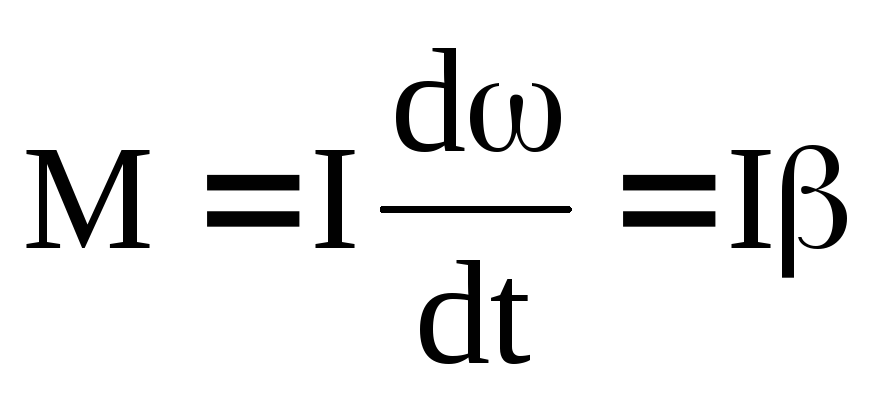
где — угловое ускорение.

Выражение (23) является уравнением динамики вращательного движения твердого тела относительно неподвижной оси, которое лучше с точки зрения причинно-следственных связей представить как:

. (24)

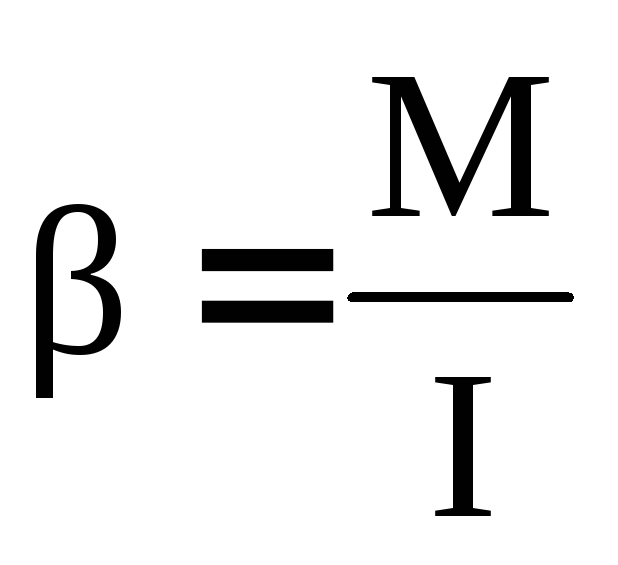
Угловое ускорение тела определяется алгебраической суммой моментов внешних сил относительно оси вращения деленной на момент инерции тела относительно этой оси.

Сопоставим основные величины и уравнения, определяющие вращение тела вокруг неподвижной оси и его поступательное движение (см. таблицу 1):

Скорость

Угловая скорость

Ускорение

Угловое ускорение

Сила

Момент силы или

Основное уравнение динамики:

Основное уравнение динамики:

Работа

Работа

Кинетическая энергия

Кинетическая энергия

Динамика поступательного движения твердого тела полностью определяется силой и массой как мерой их инертности. При вращательном движении твердого тела динамика движения определяется не силой как таковой, а ее моментом, инертность не массой, а ее распределением относительно оси вращения. Тело не приобретает углового ускорения, если сила приложена, но ее момент будет равен нулю.

Методика выполнения работы

Согласно второму закону Ньютона составим уравнение поступательного движения груза m без учета сил трения:

(25)

или в скалярном виде, т.е. в проекциях на направление движения:

. (26)

, (27)

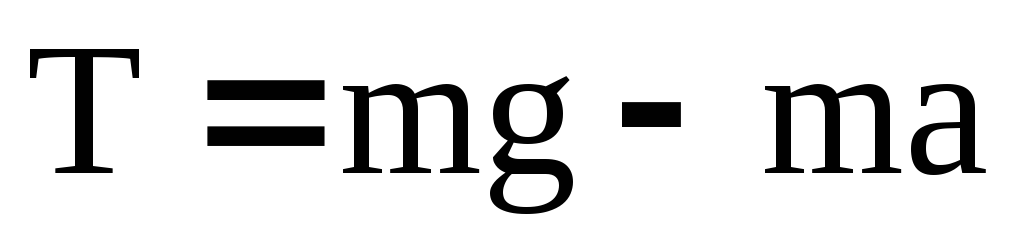
где T – сила натяжения нити. Согласно основному уравнению динамики вращательного движения (24), момент силы T, под действием которой система тел m_d, m_1, m₂ совершает вращательное движение, равен произведению момента инерции I этой системы на ее угловое ускорение :

или , (28)

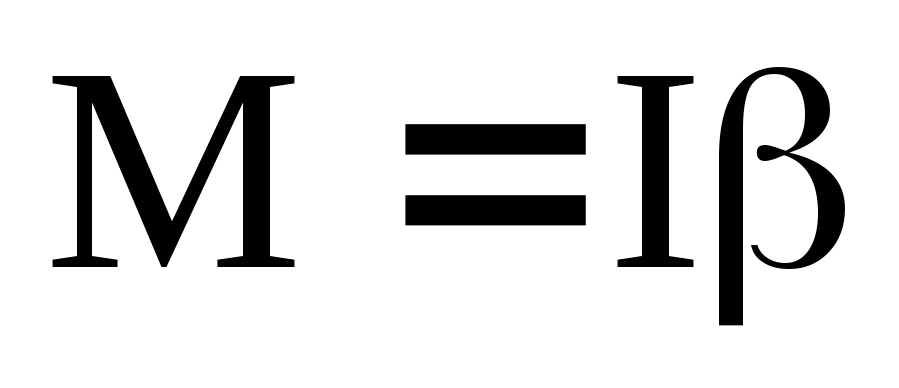
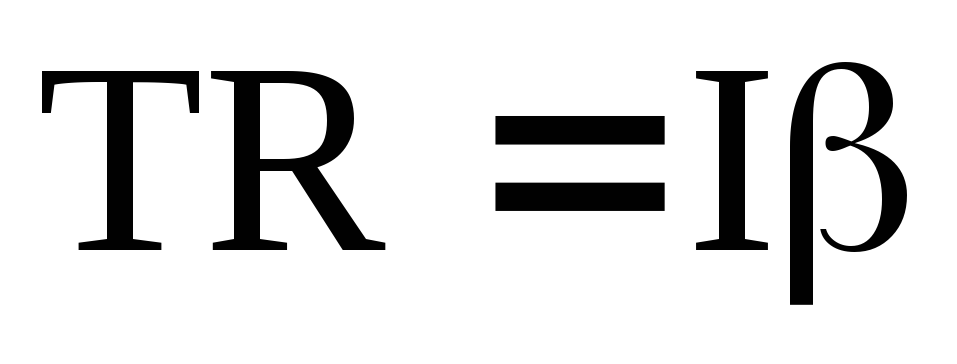
где R – плечо этой силы равное радиусу диска.

Выразим силу натяжения нити из (28):

(29)

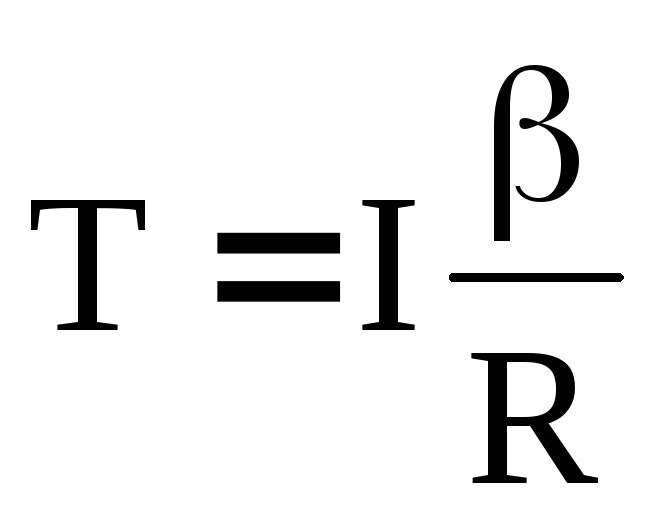
и приравняем правые части (27) и (29):

. (30)

Линейное ускорение связано с угловым следующим соотношением a=R, следовательно:

. (31)

Откуда ускорение груза m без учета сил трения в блоке равно:

. (32)

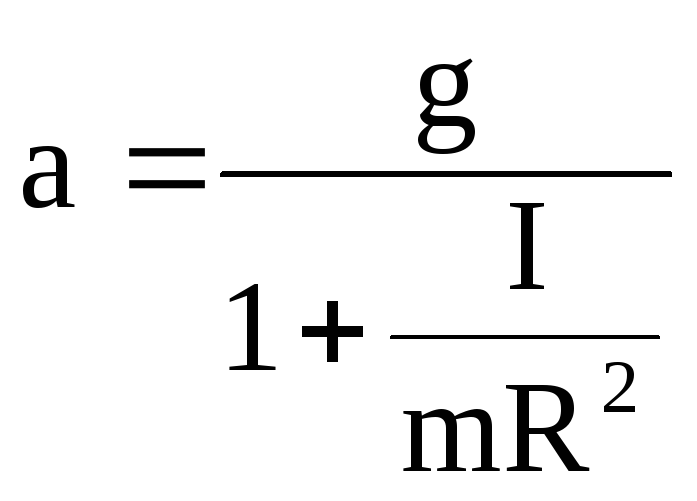
Рассмотрим динамику движения системы с учетом сил трения, которые действуют в системе. Они возникают между стержнем, на котором закреплен диск и неподвижной частью установки (внутри подшипников), а также между подвижной частью установки и воздухом. Все эти силы трения мы будем учитывать с помощью момента сил трения.

С учетом момента сил трения уравнение динамики вращения записывается следующим образом:

, (33)

где a’ – линейное ускорение при действии сил трения, M_тр – момент сил трения.

Вычитая уравнение (33) из уравнения (28), получим:

,

. (34)

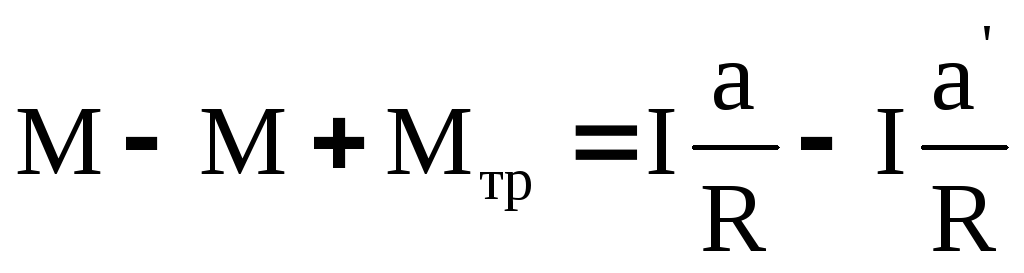
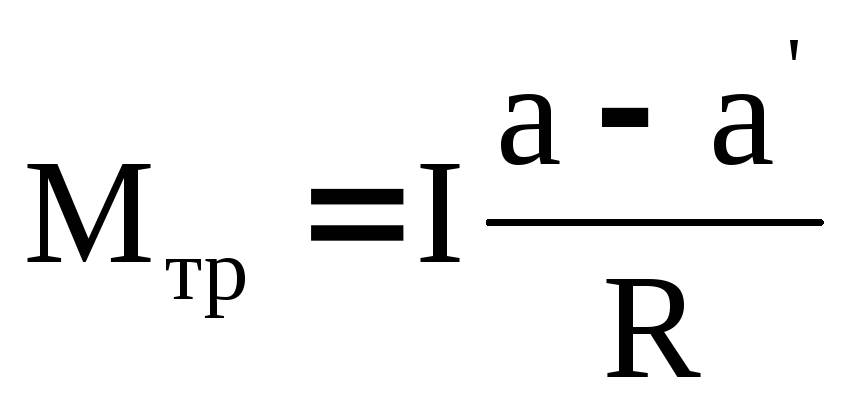
Ускорение без учета силы трения (а) можно рассчитать по формуле (32). Ускорение гирьки с учетом сил трения можно рассчитать из формулы для равноускоренного движения, измерив пройденный путь S и время t:

. (35)

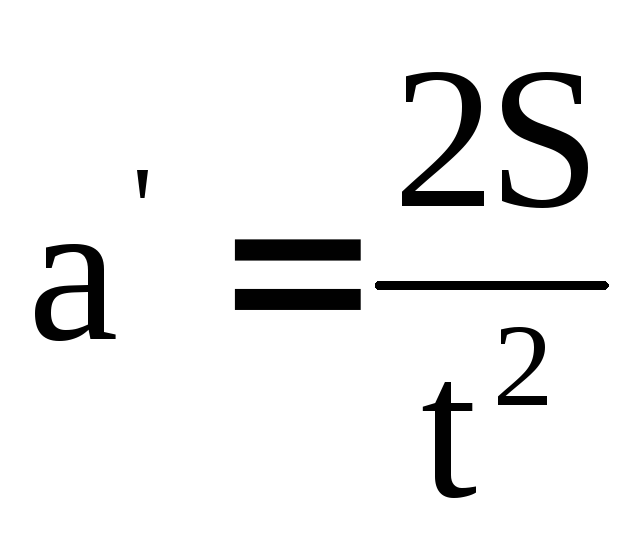
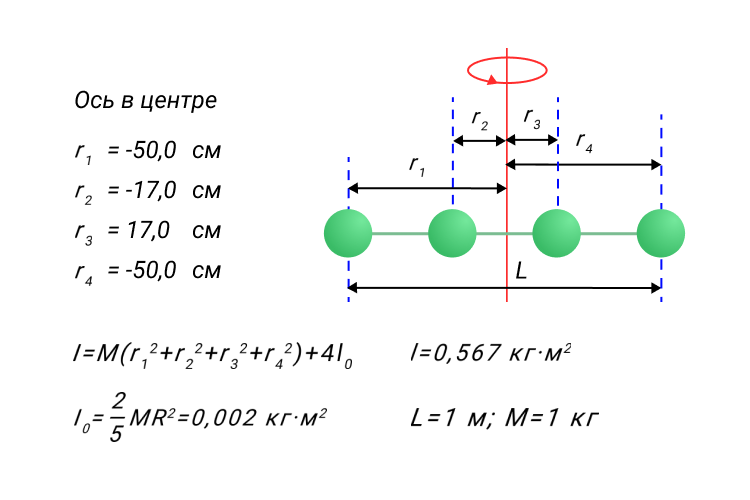
Зная значения ускорений (а и а’), по формуле (34) можно определить момент сил трения. Для расчетов необходимо знать величину момента инерции системы вращающихся тел, который будет равен сумме моментов инерции диска, стержней и грузов.

Момент инерции диска согласно (14) равен:

. (36)

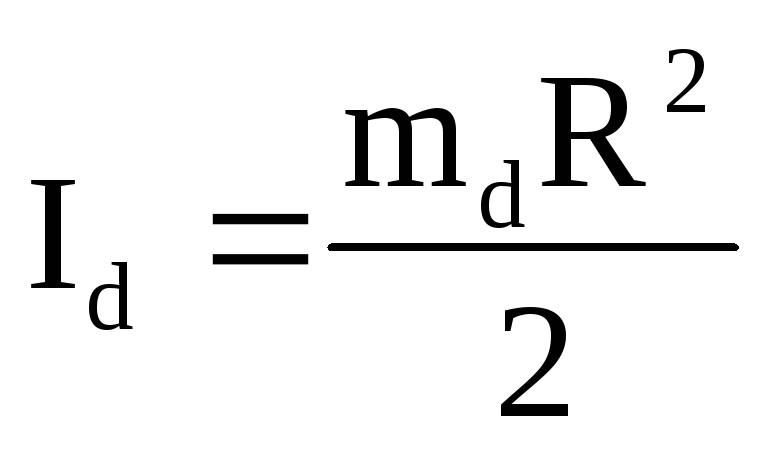
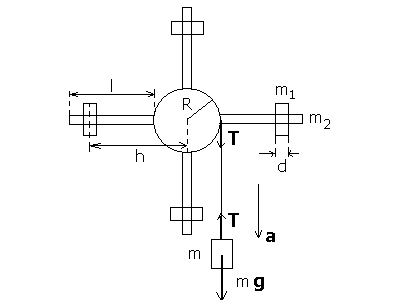
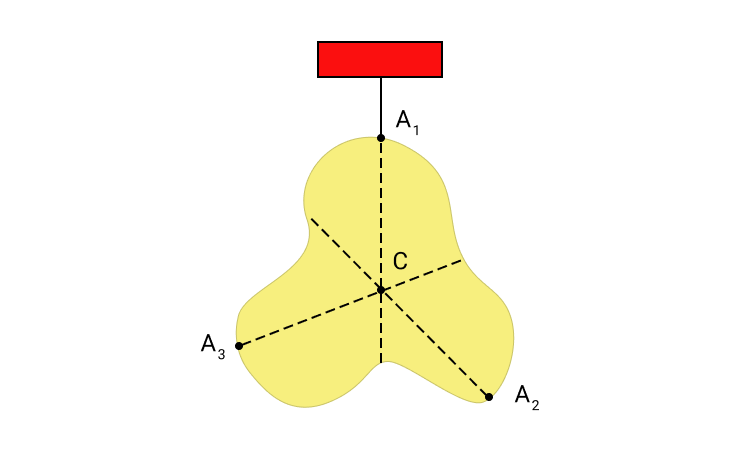
Момент инерции каждого из стержней (рис.6) относительно оси О согласно (16) и теореме Штейнера равен:

, (37)

где a_c=l/2+R, R – расстояние от центра масс стержня до оси вращения О; l – длина стержня; I_oc – его момент инерции относительно оси, проходящей через центр масс.

Аналогично рассчитываются моменты инерции грузов:

, (38)

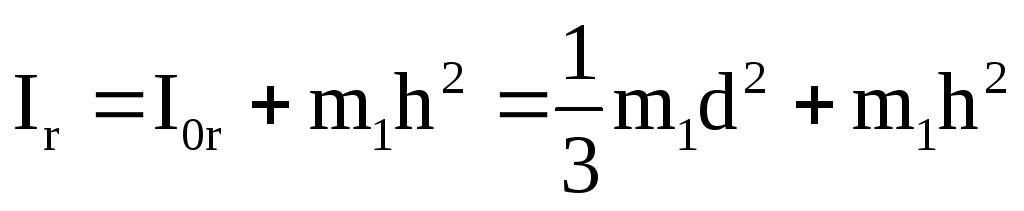
где h – расстояние от центра масс груза до оси вращения О; d – длина груза; I_0r – момент инерции груза относительно оси, проходящей через его центр масс. Сложив моменты инерции всех тел, получим формулу для вычисления момента инерции всей системы:

. (39)

Источник

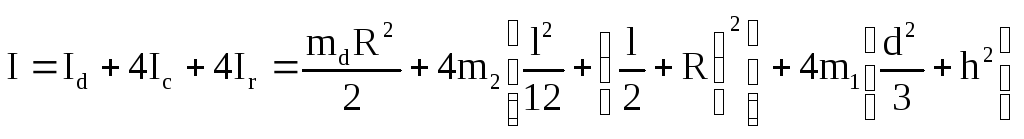
Вращение твердого тела

Углы выражаются в радианах. За положительное направление вращения принимается направление против часовой стрелки.

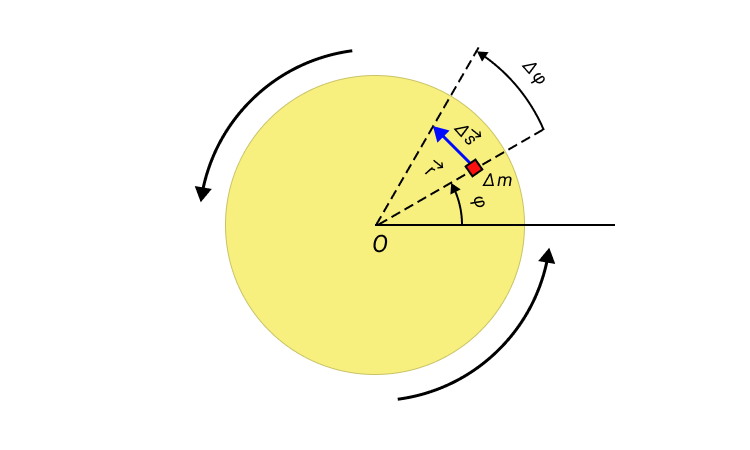
Когда твердое тело вращается относительно неподвижной оси, все точки этого тела перемещаются с одинаковыми угловыми скоростями и ускорениями.

Если угловое перемещение Δ φ мало, то модуль вектора линейного перемещения ∆ s → некоторого элемента массы Δ m вращающегося твердого тела можно выразить соотношением:

Между модулями угловой и линейной скоростей можно установить связь посредством равенства

Модули линейного и углового ускорения также взаимосвязаны:

Также нам необходимо учесть возникновение нормального или центростремительного ускорения, которое всегда возникает при движении тел по окружности.

Модуль ускорения выражается формулой:

Физическая величина ∑ i ∆ m i r i 2 носит название момента инерции I тела относительно оси вращения. Она зависит от распределения масс вращающегося тела относительно оси вращения:

Если для динамики поступательного движения основную роль играет масса тела, то в динамике вращательного движения имеет значение момент инерции. Но если масса – это свойство рассматриваемого твердого тела, которое не зависит от скорости движения и других факторов, то момент инерции зависит от того, вокруг какой оси вращается тело. Для одного и того же тела момент инерции будет определяться различными осями вращения.

В большинстве задач считается, что ось вращения твердого тела проходит через центр его массы.

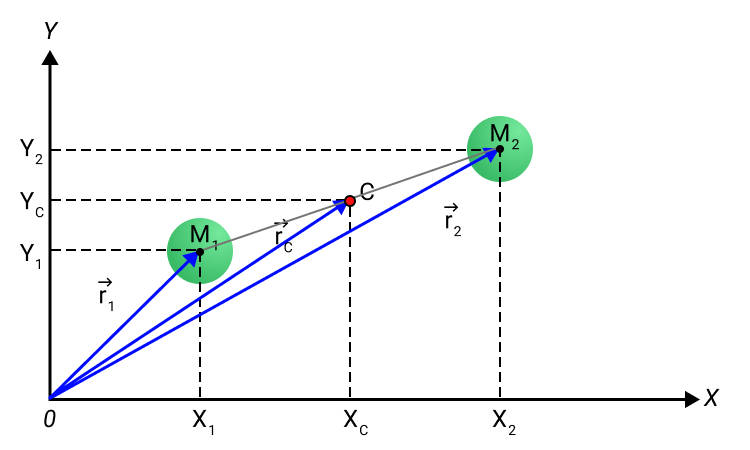
Рисунок 2. Центр масс C системы из двух частиц.

В векторной форме это соотношение принимает вид:

Аналогично, для системы из многих частиц радиус-вектор r C → центра масс определяется выражением

Если мы имеем дело с твердым телом, состоящим из одной части, то в приведенном выражении суммы для r C → необходимо заменить интегралами.

Центр масс в однородном поле тяготения совпадает с центром тяжести. Это значит, что если мы возьмем тело сложной формы и подвесим его за центр масс, то в однородном поле тяготения это тело будет находиться в равновесии. Отсюда следует способ определения центра масс сложного тела на практике: его необходимо последовательно подвесить за несколько точек, одновременно отмечая по отвесу вертикальные линии.

На рисунке мы видим тело, которое подвешено за центр масс. Оно находится в состоянии безразличного равновесия. В однородном поле тяготения равнодействующая сил тяжести приложена к центру масс.

Мы можем представить любое движение твердого тела как сумму двух движений. Первое поступательное, которое производится со скоростью центра масс тела. Второе – это вращение относительно оси, которая проходит через центр масс.

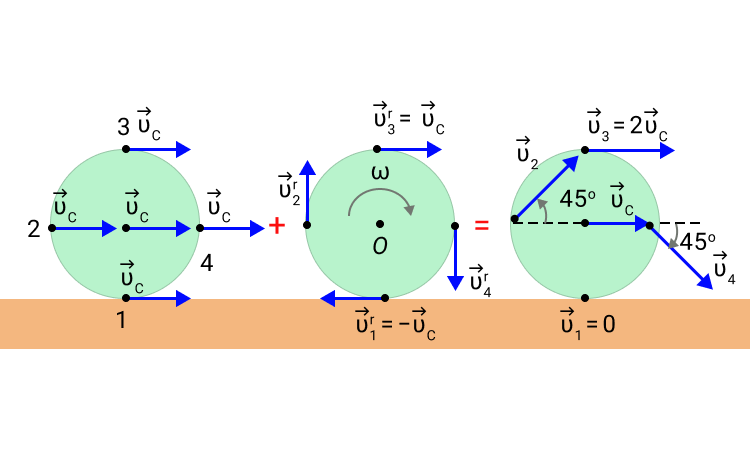
Предположим. Что у нас есть колесо, которое катится по горизонтальной поверхности без проскальзывания. Все точки колеса во время движения перемещаются параллельно одной плоскости. Такое движение мы можем обозначить как плоское.

Теорема о движении центра масс

Кинестетическая энергия вращающегося твердого тела при плоском движении будет равна сумме кинетической энергии поступательного движения и кинетической энергии вращения относительно оси, которая проведена через центр масс и располагается перпендикулярно плоскостям, в которых движутся все точки тела:

где m – полная масса тела, I C – момент инерции тела относительно оси, проходящей через центр масс.

В механике используется теорема о движении центра масс.

Любое тело или несколько взаимодействующих тел, которые представляют собой единую систему, обладают центром масс. Этот центр масс под воздействием внешних сил перемещается в пространстве как материальная точка, в которой сосредоточена вся масса системы.

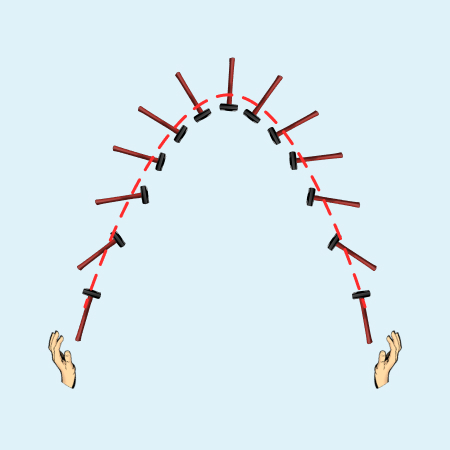
На рисунке мы изобразили движение твердого тела, на которое действуют силы тяжести. Центр масс тела движется по траектории, которая близка к параболе, тогда как траектория остальных точек тела является более сложной.

Рисунок 5. Движение твердого тела под действием силы тяжести.

Теорема Штейнера о параллельном переносе оси вращения

Рассмотрим случай, когда твердое тело движется вокруг некоторой неподвижной оси. Момент инерции этого тела инерции I можно выразить через момент инерции I C этого тела относительно оси, проходящей через центр масс тела и параллельной первой.

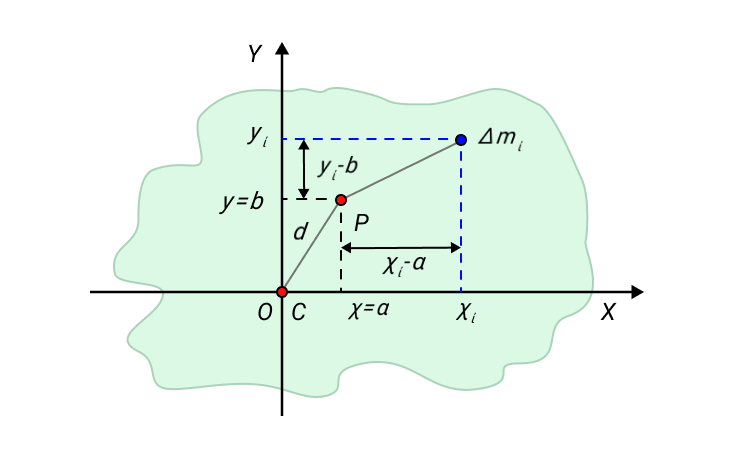
Рисунок 6. К доказательству теоремы о параллельном переносе оси вращения.

По определению момента инерции:

Выражение для I P можно переписать в виде:

Два последних члена уравнения обращаются в нуль, так как начало координат в нашем случае совпадает с центром масс тела.

Так мы пришли к формуле теоремы Штейнера о параллельном переносе оси вращения.

Для тела, которое вращается относительно произвольной неподвижной оси, момент инерции, согласно теореме Штейнера, равен сумме момента инерции этого тела относительно параллельной ей оси, проходящей через центр масс тела, и произведения массы тела на квадрат расстояния между осями.

где m – полная масса тела.

Рисунок 7. Модель момента инерции.

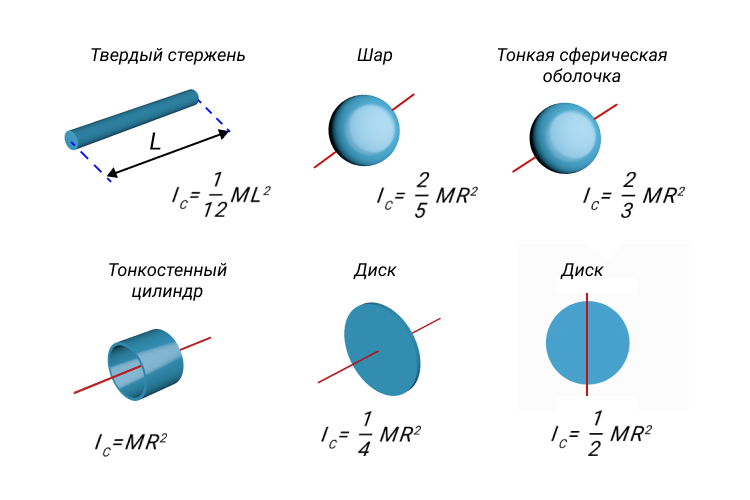
На рисунке ниже изображены однородные твердые тела различной формы и указаны моменты инерции этих тел относительно оси, проходящей через центр масс.

Рисунок 8. Моменты инерции I C некоторых однородных твердых тел.

Основное уравнение динамики вращательного движения твердого тела

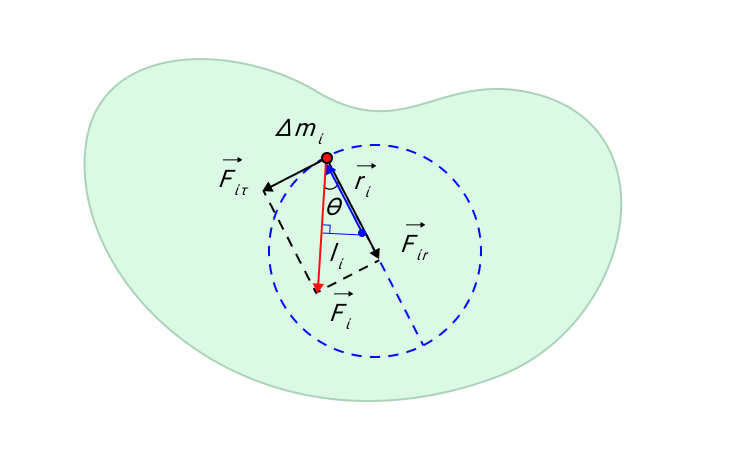
Рисунок 9. Касательная F i τ → и радиальная F i r → составляющие силы F i → действующей на элемент Δ m i твердого тела.

где ε = a i τ r i – угловое ускорение всех точек твердого тела.

Теперь нужно аналогичные соотношения записать для всех элементов массы Δm_i вращающегося твердого тела, а затем просуммировать левые и правые части. Это дает:

Стоящая в правой части сумма моментов сил, действующих на различные точки твердого тела, состоит из суммы моментов всех внешних сил и суммы моментов всех внутренних сил.

Угловое ускорение ε и момент сил M в этом уравнении являются величинами алгебраическими.

Обычно за положительное направление вращения принимают направление против часовой стрелки.

Закон сохранения момента импульса

Момент импульса вращающегося тела – это физическая величина, которая равняется произведению момента инерции тела I на угловую скорость ω его вращения.

Так мы пришли к закону сохранения момента импульса.

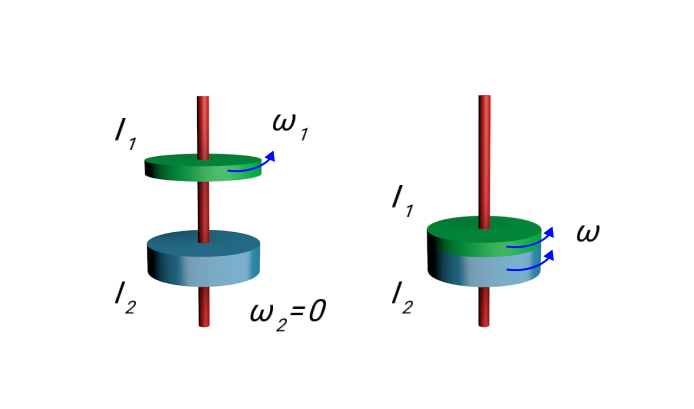
В качестве примера приведем рисунок, на котором изображено неупругое вращательное столкновение дисков, которые насажены на общую для них ось.

Мы имеем дело с замкнутой системой. Для любой замкнутой системы закон сохранения момента импульса будет справедливым. Он выполняется и в условиях экспериментов по механике, и в условиях космоса, когда планеты движутся по своим орбитам вокруг звезды.

Мы можем записать уравнение динамики вращательного движения как для неподвижной оси, так и для оси, которая перемещается равномерно или с ускорением. Вид уравнения не изменится и в том случае, если ось движется ускоренно. Для этого должно выполняться два условия: ось должна проходить через центр массы тела, а ее направление в пространстве остается неизменным.

Предположим, что у нас есть тело (шар или цилиндр), которое катится по наклонной плоскости с некоторым трением.

Рисунок 11. Качение симметричного тела по наклонной плоскости.

Уравнение вращательного движения:

Второй закон Ньютона для поступательного движения центра масс записывается в виде:

Источник