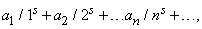теория чисел что это такое

Теория чисел

Раздел математики занимающийся изучением целых чисел и их свойств называется теория чисел или высшая арифметика.

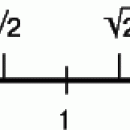
Среди целых чисел особое место занимают натуральные числа, которые можно разделить на два класса: простые и составные. К первому классу относятся числа, имеющие своими делителями два числа: единицу и само себя. Ко второму классу относятся все остальные числа.

Простые числа, их свойства и связь со всеми натуральными числами изучались Евклидом (3 век до нашей эры). Он считал, что любое число натурального ряда может быть единственным образом представлено как произведение простых чисел. В «Началах» Евклид указал способ нахождения наибольшего общего делителя (НОД) двух чисел, следствием из которого является теорема об однозначном разложении натуральных чисел на простые сомножители. С понятием наименьшего общего делителя двух чисел связано понятие их наименьшего общего кратного (НОК).

Большой вклад в развитие теории чисел внес Пьер Ферма (1601-1665), которому принадлежат открытия связанные с теорией делимости целых чисел, и теорией диофантовых уравнений. Им было сформулировано утверждение о «невозможности» — Великая теорема Ферма, доказана Малая теорема Ферма, которая в дальнейшем была обобщена Л. Эйлером. В феврале 1657 года Ферма предложил найти общее правило решение уравнения Пелля ax 2 + 1 = y 2 в целых числах. Решение этого уравнения для a = 2 было описано Евклидом в «Началах», а полное решение найдено Эйлером в 1759 году.

В 18 веке Л. Эйлер (1707-1783) первым из математиков стал создавать общие методы и применять другие разделы математики к решению задач теории чисел. Применение методов математического анализа положили начало аналитической теории чисел, в которой важное место занимают методы тригонометрических сумм, позволяющие оценивать число решений уравнений или систем уравнений в целых числах.

В аналитической теории чисел так же применяется комплексный анализ для доказательства теоремы о распределении простых чисел. Однако остается открытым вопрос, существует ли бесконечно много пар «простых близнецов», т. е. простых чисел разность, между которыми равна двум, например, 17 и 19 или 101 и 103.

Алгебраическая теория чисел расширяет понятие числа. Здесь рассматриваются алгебраические целые числа, корни многочленов с рациональными коэффициентами и старшим членом равным единице.

Элементарная теория чисел изучает целые числа без использования методов других разделов математике. Здесь рассматриваются такие вопросы как делимость целых чисел, числа Фибоначчи, построение магических квадратов, алгоритм нахождения наименьшего общего делителя и наибольшего общего кратного, малая теорема Ферма.

Многие вопросы теории чисел легко сформулировать, но трудно доказать, а ряд вопросов остаются открытыми, например, еще не найдена формулы по которой выводятся все простые числа. Великая теорема Ферма, сформулированная в 1637 году, оставалась без доказательства более 3 столетий и была доказана Уалсом в 1995 году.

Источник

Теория чисел

Теория чисел, или высшая арифметика — раздел математики, изучающий целые числа и сходные объекты. В теории чисел в широком смысле рассматриваются как алгебраические, так и трансцендентные числа, а также функции различного происхождения, которые связаны с арифметикой целых чисел и их обобщений.

Содержание

Элементарная теория чисел

В элементарной теории чисел целые числа изучаются без использования методов других разделов математики. Такие вопросы, как делимость целых чисел, алгоритм Евклида для вычисления наибольшего общего делителя и наименьшего общего кратного, разложение числа на простые множители, построение магических квадратов, совершенные числа, числа Фибоначчи, малая теорема Ферма, теорема Эйлера, задача о четырёх кубах относятся к этому разделу.

Аналитическая теория чисел

В аналитической теории чисел для вывода и доказательства утверждений о числах и числовых функциях используется мощный аппарат математического анализа. Первым шагом в этом направлении стал метод производящих функций, сформулированный Эйлером. Для определения количества целочисленных неотрицательных решений линейного уравнения вида

, где — натуральные числа,

Эйлер построил производяшую функцию, которая определяется как произведение сходящихся рядов (при ) и является суммой членов геометрической прогрессии, при этом

, где — число решений изучаемого уравнения.

Работая над доказательством теоремы Евклида о бесконечности простых чисел Эйлер рассмотрел произведение по всем простым числам и сформулировал тождество:

,

Для доказательства теоремы о бесконечности простых чисел в общем виде Дирихле использовал произведения по всем простым числам, аналогичные эйлерову произведению, и показал, что

,

Чебышев показал, что число простых чисел, не превосходяших , обозначенное как , стремится к бесконечности по следующему закону:

Другим направлением аналитической теории чисел является применение комплексного анализа в доказательстве теоремы о распределении простых чисел.

Алгебраическая теория чисел

В алгебраической теории чисел понятие числа расширяется, в качестве алгебраических чисел рассматривают корни многочленов с рациональными коэффициентами. При этом аналогом целых чисел выступают целые алгебраические числа, то есть корни унитарных многочленов с целыми коэффициентами. В отличие от целых чисел в кольце целых алгебраических чисел не обязательно выполняется свойство факториальности, то есть единственности разложения на простые множители.

Теория алгебраических чисел обязана своим появлением попыткам доказать теорему Ферма. Куммеру принадлежит равенство

, где — корни степени из единицы.

Алгебраическая теория чисел включает в себя такие разделы, как теорию дивизоров, теорию Галуа, теорию полей классов, дзета- и L-функции Дирихле, когомологии групп и многое другое.

Одним из основных приёмов является вложение поля алгебраических чисел в своё пополнение по какой-то из метрик — архимедовой (например, в поле вещественных или комплексных чисел) или неархимедовой (например, в поле p-адических чисел).

Исторический очерк

Теория чисел в древнем мире

Весомый вклад в становление теории чисел оказали пифагорейцы, Евклид и Диофант.

Теория чисел в Средние века

Дальнейшее развитие теории чисел

Вместе с тем, в теории чисел существует большое количество открытых проблем.

Источник

ЧИСЕЛ ТЕОРИЯ

Вне самой математики теория чисел имеет довольно мало приложений, и развивалась она не ради решения прикладных задач, а как искусство ради искусства, обладающее своей внутренней красотой, тонкостью и трудностью. Тем не менее теория чисел оказала большое влияние на математическую науку, поскольку некоторые разделы математики (в том числе и такие, которые впоследствии нашли применение в физике) были первоначально созданы для решения особенно сложных проблем теории чисел. См. также ЧИСЛО; МАТЕМАТИКА.

Мультипликативные основания.

Согласно теореме о единственности разложения на простые множители, простые числа являются теми «кирпичиками», из которых строятся целые числа. Помимо ± 2, все остальные простые числа нечетны, так как четным число называется только когда оно делится на 2. Уже Евклиду было известно, что простых чисел бесконечно много. Он доказал это, заметив, что число N = (p₁p₂. p_n) + 1 (где p₁, p₂. p_n – все простые числа) не делится ни на одно простое число p₁, p₂. p_n и, потому либо само N, либо один из его простых множителей должен быть простым числом, отличным от p₁, p₂. p_n. Следовательно, p₁, p₂. p_n не может быть полным перечнем всех простых чисел.

Как и в случае уравнений, можно рассматривать сравнения с одним или более неизвестными. Простейшим служит линейное сравнение с одним неизвестным ax є b (mod m). Оно выполняется только в том случае, когда m делит число (ax – b), или ax – b = my при некотором целом y. Таким образом, это сравнение эквивалентно линейному уравнению ax – my = b. Так как левая его часть обязательно делится на НОД (a, m), оно не может выполняться ни при каких целых числах x и y, если НОД (a, m) не делит число b.

Можно показать, что сравнение ax є b (mod m) разрешимо в том и только в том случае, когда НОД (a, m) делит число b, а если это условие выполнено, то существует ровно НОД (a, m) классов вычетов по модулю m, элементы которых удовлетворяют этому сравнению. Например, уравнение 2x + 6y = 5 неразрешимо в целых числах, т.к. НОД (2, 6) = 2, а число 5 не делится на 2; уравнение 2x + 3y = 5 разрешимо, т.к. НОД (2, 3) = 1; аналогично, уравнение 2x + 3y = b разрешимо при любом целом b. Действительно, при любых a и m, таких, что НОД (a, m) = 1, уравнение ax – my = b разрешимо для любого b.

Уравнение ax – my = b – это, по-видимому, простейший пример «диофантова уравнения», т.е. уравнения с целыми коэффициентами, которое требуется решить в целых числах.

Общее квадратичное сравнение ax 2 + bx + c є 0 (mod m) можно проанализировать весьма полно. Умножая на 4a, получаем 4a 2 x 2 + 4abx + 4ac є 0 (mod 4am), или (2ax + b) 2 є (b 2 – 4ac) (mod 4am). Полагая 2ax + b = u и b 2 – 4ac = r, мы сводим решение исходного сравнения к решению сравнения u 2 є r (mod 4am). В свою очередь решения последнего сравнения с помощью чуть более сложных рассуждений можно свести к решению сравнений вида u 2 є r (mod p), где p – простое число. Поэтому все сложности и весь интерес кроются в этом, казалось бы, частном случае общего квадратичного сравнения. Если сравнение u 2 є r (mod p) разрешимо, то u называется квадратичным вычетом по модулю p, а в противном случае – квадратичным невычетом. «Квадратичный закон взаимности», открытый эмпирически Эйлером (ок. 1772) и доказанный Гауссом (1801), утверждает, что если p и q – различные нечетные простые числа, то каждое из них или является квадратичным вычетом по модулю другого, или это не верно ни для одного из них за исключением случая, когда и p, и q имеют вид 4k + 3 и когда лишь одно из этих чисел является квадратичным вычетом по модулю другого. Теорема Гаусса, названная им «золотой теоремой», служит мощным инструментом теоретико-числовых исследований и позволяет ответить на вопрос, разрешимо ли данное квадратичное сравнение.

Сравнения более высоких степеней вида f (x) є 0 (mod m), где f (x) – многочлен степени выше 2, решаются с большим трудом. Согласно теореме Ж.Лагранжа (1736–1813), число решений (точнее, число классов вычетов, каждый из элементов которых является решением) не превышает степени многочлена f (x), если модуль простой. Существует простой критерий разрешимости сравнения x n є r (mod p), принадлежащий Эйлеру, но он неприменим к сравнениям общего вида, о разрешимости которых при n > 2 мало что известно.

Диофантовы уравнения.

Формы.

Если в f(x,y) произвести замену переменных x = Au + Bv, y = Cu + Dv, где A, B, C, D – целые числа, удовлетворяющие условию AD – BC = ± 1, то получим новую форму g(u,v). Так как любой паре целых чисел x и y соответствует пара целых чисел u и v, то каждое целое число, представимое формой f, представимо формой g, и наоборот. Поэтому в таком случае говорят, что f и g эквивалентны. Все формы, эквивалентные данной, образуют класс эквивалентности; число таких классов для форм с фиксированным дискриминантом D конечно.

Оказывается, что в случае положительно определенных форм в каждом классе эквивалентности существует единственная форма ax 2 + bxy + cy 2 с такими коэффициентами a, b, c, что либо –a Ј a Ј b Ј a = c. Такая форма называется приведенной формой данного класса эквивалентности. Приведенная форма используется как стандартный представитель своего класса, а информация, получаемая относительно нее, легко распространяется на остальные члены класса эквивалентности. Одной из основных задач, которая в этом простейшем случае полностью решена, является нахождение приведенной формы, эквивалентной данной форме; этот процесс называется приведением. В случае неопределенных форм мы не можем указать неравенств, которым должны удовлетворять коэффициенты лишь одной формы из каждого класса. Однако существуют неравенства, которым удовлетворяет некоторое конечное число форм в каждом классе, и все они называются приведенными формами.

Определенные и неопределенные формы различаются также тем, что любая определенная форма представляет (если представляет) целое число только конечным числом способов, тогда как число представлений целого числа неопределенной формой всегда либо равно нулю, либо бесконечно. Дело в том, что, в отличие от определенных форм, неопределенные обладают бесконечно многими «автоморфизмами», т.е. подстановками x = Au + Bv, y = Cu + Dv, оставляющими форму f (x,y) неизменной, так что f (x,y) = f (u,v). Эти автоморфизмы можно полностью описать в терминах решений уравнения Пелля z 2 + D w 2 = 4, где D – дискриминант формы f.

Сходным образом можно определить и эквивалентность квадратичных форм от n переменных. Существуют аналогичные теории приведения и представлений, естественно, более сложные, чем в случае двух переменных. К 1910 развитие теории продвинулось настолько, насколько это было возможно с помощью классических методов, и теория чисел пребывала в состоянии спячки вплоть до 1935, когда Зигель придал ей новый импульс, сделав основным инструментом исследований в этой области математический анализ.

Одна из наиболее удивительных теорем теории чисел была доказана Ферма и, по-видимому, была известна еще Диофанту. Она гласит, что любое целое число есть сумма четырех квадратов. Более общее утверждение без доказательства высказал Э.Варинг (1734–1798): каждое положительное целое число есть сумма не более девяти кубов, не более девятнадцати четвертых степеней и т.д. Общее утверждение о том, что для каждого положительного целого числа k существует целое число s, такое, что любое положительное целое число может быть представлено в виде суммы не более чем s k-х степеней, было в конце концов доказано Д.Гильбертом (1862–1943) в 1909.

Геометрия чисел.

Многие вопросы естественно приводят к теории выпуклых тел, и именно эта теория была развита Минковским наиболее полно. Затем на долгое время опять наступил застой, но с 1940, в основном благодаря работам английских математиков, наметился прогресс в развитии теории невыпуклых тел.

Диофантовы приближения.

Аналитическая теория чисел.

Математический анализ можно назвать математикой непрерывно изменяющихся величин; поэтому на первый взгляд может показаться странным, что при решении чисто теоретико-числовых задач такая математика может быть полезной. Первым, кто стал систематически использовать весьма мощные аналитические методы в арифметике, был П.Дирихле (1805–1859). Исходя из свойств «рядов Дирихле»

рассматриваемых как функции переменной s, он показал, что если НОД (a,m) = 1, то существует бесконечно много простых чисел вида p є a (mod m) (таким образом, существует бесконечно много простых чисел вида 4k + 1, а также бесконечно много простых чисел вида 4k + 3). Частный случай ряда Дирихле 1 + 2 –s + 3 –s +. получил название дзета-функция Римана z (s) в честь Б.Римана (1826–1866), который исследовал ее свойства при комплексном s, чтобы проанализировать распределение простых чисел. Задача состоит в следующем: если p (x) обозначает число простых чисел, не превышающих x, то как велико значение p (x) при больших значениях x? В 1798 А.Лежандр высказал предположение, согласно которому отношение p (x) к x/log x (где логарифм берется по основанию e) приближенно равно 1 и с возрастанием x стремится к 1. Частичный результат был получен в 1851 П.Л.Чебышёвым (1821–1894), но полностью гипотеза Лежандра, т.н. «теорема о простых числах», была доказана лишь в 1896 с помощью методов, основанных на работе Римана (независимо Ж.Адамаром и Ш. де ла Валле Пуссеном). В 20 в. в области аналитической теории чисел было сделано немало, однако многие, казалось бы, легкие вопросы относительно простых чисел по-прежнему остаются без ответа. Например, поныне неизвестно, существует ли бесконечно много «пар простых чисел», т.е. пар последовательных простых чисел, таких, как 101 и 103. Существует еще одна до сих пор недоказанная гипотеза Римана, она касается комплексных чисел, являющихся нулями дзета-функции, и занимает настолько важное место во всей теории, что многие доказанные и опубликованные теоремы содержат слова «Если гипотеза Римана верна, то. ».

Аналитические методы широко применяются и в аддитивной теории чисел, занимающейся представлениями чисел в виде сумм определенного вида. Аналитические методы были существенно использованы Гильбертом в его решении проблемы Варинга, о которой упоминалось выше. Попытки придать теореме Гильберта количественный характер с помощью оценки числа k-х степеней, необходимых для представления всех целых чисел, привели в 1920-х и 1930-х годах Г.Харди и Дж.Литлвуда к созданию кругового метода, усовершенствованного далее И.М.Виноградовым (1891–1983). Эти методы нашли применение в аддитивной теории простых чисел, например, при доказательстве теоремы Виноградова о том, что каждое достаточно большое нечетное число представимо в виде суммы трех простых чисел.

Алгебраическая теория чисел.

Чтобы доказать закон взаимности четвертых степеней (аналог квадратичного закона взаимности для соотношения x 4 є q (mod p)), Гаусс в 1828 исследовал арифметику комплексных чисел a + bi, где a и b – обычные целые числа, а 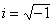. Делимость, «единицы», простые числа и НОД для «гауссовых чисел» определяются так же, как для обычных целых чисел, сохраняется также и теорема о единственности разложения на простые числа. Пытаясь доказать Великую теорему Ферма (о том, что уравнение x n + y n = z n не имеет решений в целых числах при n > 2), Э.Куммер в 1851 перешел к изучению арифметики целых чисел более общего типа, определяемых с помощью корней из единицы. Сначала Куммер полагал, что ему удалось найти доказательство теоремы Ферма, но он заблуждался, поскольку, вопреки наивной интуиции, для таких чисел не выполняется теорема о единственности разложения на простые множители. В 1879 Р.Дедекинд ввел общее понятие алгебраического целого числа, т.е. алгебраического числа, удовлетворяющего алгебраическому уравнению с целочисленными коэффициентами и коэффициентом a₀ при старшем члене, равном 1. Чтобы получить некоторое множество алгебраических целых чисел, аналогичное множеству обычных целых чисел, необходимо рассматривать только такие алгебраические целые числа, которые принадлежат фиксированному полю алгебраических чисел. Это множество всех чисел, которые можно получить из некоторого данного числа и рациональных чисел с помощью многократного применения сложения, вычитания, умножения и деления; поле алгебраических чисел аналогично множеству рациональных чисел. Алгебраические целые числа из данного поля в свою очередь подразделяются на «единицы», простые и составные числа, но в общем случае для двух таких чисел однозначно определенного НОД не существует и не выполняется теорема о единственности разложения на простые множители. Простейшие примеры полей алгебраических чисел, кроме множества рациональных чисел, это поля алгебраических чисел, определенные с помощью алгебраических чисел степени 2, т.е. иррациональных чисел, удовлетворяющих квадратным уравнениям с рациональными коэффициентами. Такие поля называются квадратичными числовыми полями.

Куммеру принадлежит фундаментальная идея введения новых т.н. идеальных чисел (1847), выбираемых таким образом, чтобы в расширенном множестве снова выполнялась теорема о единственности разложения на простые множители. Для той же цели Дедекинд в 1870 ввел несколько иное понятие идеалов, а Кронекер в 1882 – метод разложения многочлена с рациональными коэффициентами на неприводимые множители над полем рациональных чисел. Работы этих трех математиков не только заложили основы арифметической теории алгебраических чисел, но и ознаменовали начало современной абстрактной алгебры.

Вопрос о том, имеет ли место в данном поле единственное разложение на простые множители, весьма труден. Ситуация ясна только в одном случае: существует лишь конечное число квадратичных полей, обладающих этим свойством, и все такие поля, за исключением одного сомнительного случая, хорошо известны. С «единицами» поля ситуация проще: как показал Дирихле, все «единицы» (которых, вообще говоря, бесконечно много) можно представить в виде произведений степеней некоторого конечного множества «единиц». Рассмотрение такого рода проблем в связи с каким-нибудь конкретным полем непременно предваряет более глубокие арифметические исследования в рамках этого поля и приложения к проблемам классической теории чисел. Существует другая, более тонкая теория, начало которой было положено в 1894 Гильбертом, в которой одновременно рассматриваются все числовые поля, обладающие определенными свойствами. Она называется «теорией полей классов» и принадлежит к наиболее строгим в техническом отношении разделам математики. Существенный вклад в ее развитие внесли Ф.Фуртвенглер в 1902 и Т.Такаги в 1920. В последние годы в этой области математики наблюдается значительная активность.

Источник