уравнение первого начала термодинамики выглядит так

Первое начало термодинамики

теория по физике 🧲 термодинамика

Первое начало термодинамики (первый закон термодинамики) представляет собой закон сохранения энергии в тепловых процессах.

Первое начало термодинамики

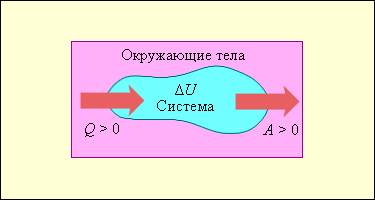
Внутренняя энергия идеального газа изменяется двумя способами: за счет теплопередачи или при совершении работы.

Внимание! Знак перед работой показывает, как процесс совершения работы влияет на изменение внутренней энергии газа.

Пример №1. В некотором процессе внутренняя энергия газа уменьшилась на 300 Дж, а газ совершил работу 500 Дж. Какое количество теплоты было сообщено газу?

Чтобы рассчитать количество теплоты, сообщенное газу, нужно найти разность между изменением внутренней энергии и работой, совершенным газом. Для этого нужно правильно определить их знаки. Так как внутренняя энергия уменьшилась, она отрицательна. Но работа положительна. Поэтому газу было сообщено следующее количество теплоты:

Q = A – U = 500 – 300 = 200 (Дж)

Зависимость физических величин

Выясним, от чего зависят величины, входящие в формулу первого начала термодинамики. Изменение внутренней энергии идеального газа зависит от изменения температуры:

Работа идеального газа зависит от изменения его объема:

Первое начало термодинамики для изопроцессов

Адиабатный (система не получает тепло извне и не отдает его окружающей среде, или Q = 0)

Пример №2. Идеальный одноатомный газ находится в сосуде с жесткими стенками объемом 0,6 куб. м. При нагревании его внутренняя энергия увеличилась на 18 кДж. На сколько возросло давление газа?

Внутреннюю энергию газа можно определить по формуле:

Отсюда изменение температуры равно:

Уравнение состояния идеального газа для 1 и 2 состояния:

Отсюда давления равны:

Графические задачи на первое начало термодинамики

Рассмотрим графический способ решения задачи на первое начало термодинамики на конкретном примере.

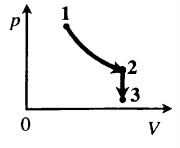
Задача: Один моль идеального одноатомного газа сначала изотермически расширился (T₁ = 300 К). Затем газ охладили, понизив давление в 3 раза (см. рисунок). Какое количество теплоты отдал газ на участке 2–3?

1. Определить температуры для всех указанных точек, учитывая графики процессов, масштаб и условие задачи.

2. Определить, к какому изопроцессу относится тот участок графика, о котором спрашивают в задаче.

Участок 2–3 на графике — это изохорный процесс, так как давление остается постоянным.

3. Записать для него первое начало термодинамики.

5. Подставляя в первое начало термодинамики формулы для расчета изменения внутренней энергии и работы газа, решить задачу.

Формула изменения внутренней энергии газа:

Формула работы газа:

Так как процесс изохорный, работа газа равна нулю. Поэтому количество теплоты, отданное газом на участке 2–3, равно изменению внутренней энергии газа:

Изменение внутренней энергии равно:

Алгоритм решения

Решение

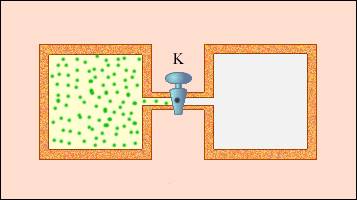
Так как это твердые тела, поверхности которых соприкасаются друг с другом, и перенос тепла происходит без переноса вещества, то этот вид теплопередачи является теплопроводностью. Тепло всегда направлено от более нагретого тела к менее нагретому.

На рисунке видно, что самым нагретым телом является нижний брусок, так как он только отдает тепло, но не принимает его. Средний брусок справа менее нагрет, чем нижний, так как принимает от него тепло. Но он более теплый по сравнению со средним бруском слева, так как он делится с ним теплом. И оба этих бруска отдают свою энергию верхнему бруску, который сам только принимает тепло, но не отдает его. Следовательно, именно он имеет температуру +40 о С.

pазбирался: Алиса Никитина | обсудить разбор | оценить

Один моль аргона, находящийся в цилиндре при температуре T₁=600 K и давлении p₁=4⋅10 5 Па, расширяется и одновременно охлаждается так, что его температура при расширении обратно пропорциональна объёму. Конечное давление газа p₂=10 5 Па. Какое количество теплоты газ отдал при расширении, если при этом он совершил работу A=2493 Дж?

Источник

Уравнение первого начала термодинамики выглядит так

Ранние работы по термодинамике были посвящены описанию количественных соотношений между теплотой и другими формами энергии. В настоящее время в этой области научных исследований наблюдается сдвиг от анализа энергетических изменений, сопровождающих превращения материи, в сторону использования термодинамики в качестве инструмента необходимого для понимания и предсказания поведения систем в связи с их энергетическими характеристиками.

Однако, термодинамика не отвечает на вопрос о том, какова величина теплового барьера, который должен быть преодолен для того, чтобы реакция пошла самопроизвольно. т.е. термодинамика изучает в основном конечные, равновесные состояния. Скорости и механизм реакции рассматривается в разделе, который носит название кинетики.

2.1. Первый закон термодинамики.

Начнем с определения.

Понятия энергии. Под понятием энергия обычно понимают “способность производить работу”. Решая какую-либо задачу методами термодинамики, необходимо прежде всего выделить из окружающего мира какую-то систему. Это может быть дождевая капля, двигатель, организм, планета и т.д. Если говорят, что выделенная система гомогенна, это означает, что свойства системы одинаковы во всех частях и система непрерывна от точки к точке. Если говорят, что система гетерогенна, это означает, что в ней присутствует не менее двух областей называемых фазами, которые отделены друг от друга поверхностями, называемыми границами раздела системы бывают двух типов: открытые и закрытые. В закрытой системе в ходе процесса происходит изменение энергии, но масса остается постоянной. В открытой системе может изменяться как энергия, так и масса.

Состояние системы определяется ее свойствами. Если изменяется одно из свойств, состояние системы меняется. При изучении системы обычно рассматриваются такие свойства, которые легко измерить. Это, в частности, температура, давление, объем, состав. Некоторые свойства взаимосвязаны, поэтому нет необходимости измерять их все одновременно.

К сожалению наши знания и возможности не позволяют вычислить (определить) весь запас энергии системы. Поэтому используется сравнительный подход. Часто энергия системы сравнивается с каким-либо стандартом (стандартным состоянием). Например газ обычно сравнивается с идеальным газом при стандартных условиях. Жидкий растворитель сравнивается с чистой жидкостью. Твердое вещество с его наиболее стабильной кристаллической формой. Такие состояния, называемые стандартными, представляют собой точки отсчета, относительно которых измеряют изменение в системе.

2.2 Формулировка первого закона

Есть несколько формулировок первого закона термодинамики. Если одна из них принимается в качестве основной, то все другие являются следствиями, вытекающими из нее.

Первая формулировка звучит следующим образом:

Энергия не создается и не уничтожается. Возможны лишь превращения энергии из одного вида в другой в строго эквивалентных количествах.

Следствием из этого закона является то, что невозможен вечный двигатель первого рода, т.е. нельзя создать такой двигатель, который совершил бы работу без затраты энергии. Создание такого двигателя возможно только в том случае, если неверен первый закон.

Внутренняя энергии изолированной системы есть величина постоянная.

Если данной системе передается некоторое количество энергии в форме тепла Q, которое идет только на приращение внутренней энергии системы D U и на совершение системой работы W, то согласно первому началу:

для бесконечно малых изменений:

Уравнения (1) и (2) являются математическим выражением первого начала термодинамики.

Справедливость этого утверждения можно доказать следующим образом.

Предположим, что в состоянии (I) внутренняя энергия системы U₁. Из этого состояния система переходит в состояние (2), в котором ее внутренняя энергия равна U₂.

В отличие от D U величины Q и W в общем случае зависят от пути процесса. Поэтому в уравнении (2) dU является полным дифференциалом, в то время как d Q и d W просто бесконечно малыми величинами

2.3. Применение первого начала термодинамики к различным процессам.

Если система совершает работа W только против внешнего давления, то

или для эмпирического процесса

Математическое выражение первого начала термодинамики в этом случае имеет вид:

или d Q = dU + pdV (6)

Для изохорного процесса (V = const) p D V = 0 и следовательно :

где Q_V теплота, сообщаемая системе в изохорном процессе. Из уравнения (7) и (8) следует, что в изохорном процессе тепла, сообщаемое системе, идет только на приращение внутренней энергии системы. В этом случае Q_V не зависит от пути перехода системы из одного состояния в другое и d Q_v является полным дифференциалом, т.е. функцией состояния.

Это означает, что изменение внутренней энергии системы D U в изохорном процессе определяется теплотой процесса Q_v и может быть измерено калориметрически.

В случае изобарного процесса (р= const).

Эту функцию состояния называют энтальпия и обозначают

Из уравнений (9 ) и ( 10) следует, что

Таким образом, в изобарном процессе все тепло сообщенное системе идет на приращение ее энтальпии. В этом случае Q_p также не зависит от луча перехода системы из одного состояния в другое и d Q_р является полным дифференциалом.

Из уравнения(11) и(12) следует также, что изменение энтальпии системы D Н в изобарном процессе определяется теплотой процесса Q_p и может быть измерено калориметрически.

В адиобатном процессе, т.е. в процессе, в котором система не обменивается с окружающей средой теплотой работа совершается за счет уменьшения внутренней энергии системы:

Изотермический процесс характеризуется T = const, для такого процесса dU = 0, тогда d Q = D W_T, т.е. вся сообщенная системе теплота превращается в работу, величина которой определяется уравнением:

Используя уравнение состояния газа Менделеева-Клапейрона, найдем, что для 1 моль идеального газа :

2.4. Теплота химической реакции.

Установим связи между Q_p и Q_v.

В соответствии с уравнение (10) имеем:

D Н = D U + p D V, но из уравнения (11) и (7) следует, что

Q_p = D Н, а D Н = D U, то Q_p = Q_v + p D V

Другими словами, D n изменение числа молей реагирующих веществ в результате протекания реакции.

Если реакция протекает в конденсированной системе, то объем системы меняется мало и в этом случае Q_p и Q_v приблизительно равны.

Изучая тепловые эффекты разных химических реакций, русский ученый Г.М. Гесс в 1840 году установил закон, который назван его именем.

Закон утверждает, что “теплота химической реакции, протекающей при постоянном объеме или постоянном давлении, определяется только природой исходных веществ и продуктов и не зависит от числа и последовательности промежуточных стадий при условии, что теплоты измерены при одинаковых температурах”.

Интересно, что закон Гесса был открыт раньше установления первого начала термодинамики. После установления первого начала стало ясно, что закон Гесса является одним из следствий этого начала, согласно которому Q_v = D U и Q_p = D H не зависят от пути процесса. Закон Гесса имеет большое практическое значение,т.к. позволяет рассчитать теплоты химических реакций, для которых они не могут быть определены экспериментально или это очень сложно сделать. Обычно для этого решают систему термохимических уравнений. Термохимическим называют такое уравнение, в котором в правой части наряду с химическими формулами продуктов реакции указывают теплоту реакции. При этом для реагирующих веществ указывается агрегатное состояние участников реакции. Если вещество в твердом состоянии существует в нескольких полиморфных модификациях, то необходимо указать эту модификацию.

Стехиометрические коэффициенты могут быть и дробными, т.к. они указывают молярные количества реагирующих веществ.

С термохимическими уравнениями можно проводить такие же математические операции, как и с алгебраическими уравнениями. Например, превращение глюкозы в молочную кислоты, при анаэробной ферментации используется некоторыми микроорганизмами для получения энергии.

Непосредственно измерить теплоту этого процесса трудно, поскольку параллельно с молочной кислотой образуются и другие продукты.

Однако можно экспериментально определить теплоты следующих реакции:

Вычитая из уравнения 1 удвоенное 2 и затем 3, получим:

2.6. Следствие из закона Гесса

Расчеты теплот химических реакций с использованием закона Гесса значительно упрощается, если воспользоваться так называемыми стандартными теплотами горения.

а) Расчет теплового эффекта химической реакции постандартным теплотам образования.

Стандартной теплотой образования вещества называют теплоту, которая выделяется или поглощается при образовании одного моля данного вещества в стандартном состоянии из простых веществ, взятых в стандартном состоянии при данной температуре.

Согласно проведенной формулировке теплотой образования СаСо₃ будет тепловой эффект следующей реакции:

Из закона Гесса следует, что теплота химической реакции равна алгебраической сумме теплот образования реагирующих веществ с учетом их стехиометрических коэффициентов, причем теплоты образования продуктов реакции берут со знаком плюс, а теплоты образования исходных веществ со знаком минус.

Рассмотрим в качестве примеров реакцию получения глюкозы из СО₂ и Н₂О

Суммарное уравнение реакции можно записать:

Приведение уравнения можно получить следующим образом.

Умножим уравнение 1 и 2 на 6, а затем их сумму вычтем из уравнения 3:

После алгебраических преобразований получим:

Воспользовавшись стандартными значениями теплот образования участников реакции, получим:

б) Расчеты теплот сгорания.

Стандартной теплотой сгорания называют теплоту, выделяющегося при окислении одного моля вещества, взятого в стандартном состоянии при данной температуре, кислородом до конечного продуктов окисления.

Из закона Гесса следует, что теплота химической реакции равна алгебраической сумме теплот сгорания реагирующих веществ с учетом их стехиометрических коэффициентов, причем, теплоты сгорания продуктов реакции берут со знаком минус, а теплоты сгорания исходных веществ со знаком плюс:

в) Теплота нейтрализации.

Теплотой нейтрализации называют теплоту, необходимую для нейтрализации одного мольэквивалента кислоты одним моль-эквивалентом основания.

Теплота нейтрализации сильных кислот сильными основаниями не зависит от природы кислоты и основания.

Тепловой эффект приведенных реакции практически одинаков и равен

В случае реакции нейтрализации слабых кислот и слабых оснований такого постоянства не наблюдается, так как часть тепла расходуется на ионизацию слабой кислоты или слабого основания.

г) Теплота растворения

В зависимости от природы растворенного вещества и природы растворителя процесс растворения сопровождается выделением или поглощением тепла.

Мольной теплотой растворения называют количество тепла, выделяющееся и поглощающееся при растворении одного моля вещества. в таком объеме растворителя, когда его дальнейшее прибавление не вызывает выделение или поглощение тепла.

Обычно при определении теплоты растворения берется более чем 300-кратный избыток растворителя.

Теплота растворения твердых тел представляет собой теплоту разрушения кристаллической решетки D Нр и теплоту сольватации D Нс

D Н_раств. = D Нр + D Нс

Для разрушения кристаллической решетки необходимо затратить некоторое к-во энергии, поэтому теплота этого процесса будет положительна.

Сольватация всегда сопровождается выделением тепла и, следовательно, теплота этого процесса отрицательна. Отсюда следует, что теплота растворения может быть как положительной, так и отрицательной.

Отрицательная теплота растворения указывает на то, что количество теплоты, выделяющееся при сольватации, больше, чем энергия, необходимая для разрушения кристаллической решетки. В случае положительной теплоты растворения количество энергии, необходимое для разрушения кристаллической решетки, больше энергии, которая выделяется при сольватации.

В тех случаях, когда в качестве растворителя используют воду, теплота, которая выделяется при взаимодействии растворенного вещества с растворителем, называется теплотой гидратации.

Теплоту гидратации, в соответствии с законом Гесса, расчитывают по разности между теплотой растворения безводного соединения и теплотой растворения гидрата.

Указанное уравнение можно получить комбинацией следующих

Вычтем из уравнения 1 уравнение 2:

После преобразования получим:

Источник

Первый закон термодинамики.

Первое начало (первый закон) термодинамики — это закон сохранения и превращения энер­гии для термодинамической системы.

Согласно первому началу термодинамики, работа может совершаться только за счет теплоты или какой-либо другой формы энергии. Следовательно, работу и количество теплоты измеряют в одних единицах — джоулях (как и энергию).

Первое начало термодинамики было сформулировано немецким ученым Ю. Л. Манером в 1842 г. и подтверждено экспериментально английским ученым Дж. Джоулем в 1843 г.

Первый закон термодинамики формулируется так:

Изменение внутренней энергии системы при переходе ее из одного состояния в другое равно сумме работы внешних сил и количества теплоты, переданного системе:

где ΔU — изменение внутренней энергии, A — работа внешних сил, Q — количество теплоты, переданной системе.

При любых процессах, происходящих в изолированной системе, ее внутренняя энергия остается постоянной.

Если работу совершает система, а не внешние силы, то уравнение (ΔU = A + Q) записывается в виде:

,

Количество теплоты, переданное системе, идет на изменение ее внутренней энергии и на совершение системой работы над внешними телами.

Первое начало термодинамики может быть сформулировано как невозможность существования вечного двигателя первого рода, который совершал бы работу, не черпая энергию из какого-либо источника (т. е. только за счет внутренней энергии).

Следует помнить, что как работа, так и количество теплоты, являются характеристиками процесса изменения внутренней энергии, поэтому нельзя говорить, что в системе содержится опреде­ленное количество теплоты или работы. Система в любом состоянии обладает лишь определенной внутренней энергией.

Рассмотрим применение первого закона термодинамики к различным термодинамическим процессам.

Изохорный процесс.

Зависимость р(Т) на термодинамической диаграмме изображается изохорой.

Изохорный (изохорический) процесс — термодинамический процесс, происходящий в систе­ме при постоянном объеме.

Изохорный процесс можно осуществить в газах и жидкостях, заключенных в сосуд с постоянным объемом.

При изохорном процессе объем газа не меняется (ΔV= 0), и, согласно первому началу термоди­намики ,

т. е. изменение внутренней энергии равно количеству переданного тепла, т. к. работа (А = рΔV=0) газом не совершается.

Источник

Первый закон термодинамики. Как рассказать просто о сложном?

Термодинамика — раздел физики, в котором изучаются процессы изменения и превращения внутренней энергии тел, а также способы использования внутренней энергии тел в двигателях.

1. Определение первого закона термодинамики

Термодинамика — раздел физики, в котором изучаются процессы изменения и превращения внутренней энергии тел, а также способы использования внутренней энергии тел в двигателях. Собственно, именно с анализа принципов первых тепловых машин, паровых двигателей и их эффективности и зародилась термодинамика. Можно сказать, что этот раздел физики начинается с небольшой, но очень важно работы молодого французского физика Николя Сади Карно.

Самым важным законом, лежащим в основе термодинамики является первый закон или первое начало термодинамики. Чтобы понять суть этого закона, для начала, вспомним что называется внутренней энергией. ВНУТРЕННЯЯ ЭНЕРГИЯ тела — это энергия движения и взаимодействия частиц, из которых оно состоит. Нам хорошо известно, что внутреннюю энергию тела можно изменить, изменив температуру тела. А изменять температуру тела можно двумя способами:

Нам, также известно, что работа, совершаемая газом, обозначается А_г, а количество переданной или полученной внутренней энергии при теплообмене называется количеством теплоты и обозначается Q. Внутреннюю энергию газа или любого тела принято обозначать буквой U, а её изменение, как и изменение любой физической величины, обозначается с дополнительным знаком Δ, то есть ΔU.

Сформулируем ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ для газа. Но, прежде всего, отметим, что когда газ получает некоторое количество теплоты от какого-либо тела, то его внутренняя энергия увеличивается, а когда газ совершает некоторую работу, то его внутренняя энергия уменьшается. Именно поэтому первый закон термодинамики имеет вид:

Так как работа газа и работа внешних сил над газом равны по модулю и противоположны по знаку, то первый закон термодинамики можно записать в виде:

Понять суть этого закона довольно просто, ведь изменить внутреннюю энергию газа можно двумя способами: либо заставить его совершить работу или совершить над ним работу, либо передать ему некоторое количество теплоты или отвести от него некоторое количество теплоты.

2. Первый закон термодинамики в процессах

Применительно к изопроцессам первый закон термодинамики может быть записан несколько иначе, учитывая особенности этих процессов. Рассмотрим три основных изопроцесса и покажем, как будет выглядеть формула первого закона термодинамики в каждом из них.

3. Применение

Первое начало термодинамики (первый закон) имеет огромное значение в этой науке. Вообще понятие внутренней энергии вывело теоретическую физику 19 века на принципиально новый уровень. Появились такие понятия как термодинамическая система, термодинамическое равновесие, энтропия, энтальпия. Кроме того, появилась возможность количественного определения внутренней энергии и её изменения, что в итоге привело учёных к пониманию самой природы теплоты, как формы энергии.

Ну, а если говорить о применении первого закона термодинамики в каких-либо задачах, то для этого необходимо знать два важных факта. Во-первых, внутренняя энергия идеального одноатомного газа равна: 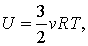а во-вторых, работа газа численно равна площади фигуры под графиком данного процесса, изображённого в координатах p—V. Учитывая это, можно вычислять изменение внутренней энергии, полученное или отданное газом количество теплоты и работу, совершённую газом или над газом в любом процессе. Можно также определять коэффициент полезного действия двигателя, зная какие процессы в нём происходят.

Источник

Первый закон термодинамики

Первый закон термодинамики представляет собой некое обобщение закона сохранения и превращения энергии для термодинамической системы, и формулируется следующим образом:

Формула первого закона термодинамики, зачастую записывается в ином виде:

Количество теплоты, полученное системой, идет на изменение ее внутренней энергии и совершение работы над внешними телами.

Первый закон термодинамики представляет из себя, по сути, обобщение опытных фактов. Если руководствоваться им, то можно заявить, что энергия не возникает и не исчезает бесследно, а передается от одной системы к другой, меняя свои формы. Невозможность создания вечного двигателя (perpetuum mobile) первого рода, то есть машины, которая может совершать полезную работу, не потребляя энергию извне и не претерпевая каких-либо изменений во внутренней конструкции агрегата, являлась важным следствием первого закона термодинамики. В подтверждение этого выступает тот факт, что каждая из огромного множества попыток создания такого устройства неизменно заканчивалась неудачей. Реальная машина может совершать положительную работу A над внешними объектами, только получая некоторое количество теплоты Q от окружающих тел или уменьшая Δ U своей внутренней энергии.

Первый закон термодинамики в процессах газов

Первый закон термодинамики может применяться к изопроцессам в газах.

В этом случае справедливой будет формула внутренней энергии газа:

Первый закон термодинамики для изобарного процесса дает:

Первый закон термодинамики для изотермического процесса выражается соотношением

Вместе с изохорным, изотермическим и изобарным процессами в термодинамике нередко исследуют процессы, происходящие в условиях отсутствующего теплообмена с окружающими объектами.

Адиабатическая оболочка – это сосуд с теплонепроницаемыми стенками.

Процессы сжатия или расширения газа в подобных емкостях называют адиабатическими.

Выходит, что газ производит работу за счет падения значения его внутренней энергии.

Работа газа в адиабатическом процессе выражается через температуры начального T 1 и конечного T 2 состояний и принимает вид:

Адиабатический процесс относится к изопроцессам.

Любые изопроцессы, в том числе и адиабатические, являются квазистатическими. Промежуточные состояния газа в таких процессах близки к состояниям термодинамического равновесия. Каждая точка, принадлежащая адиабате, описывает равновесное состояние. Однако, процесс, который проводится в адиабатической оболочке, то есть при отсутствующем теплообмене с окружающими объектами, не обязательно удовлетворяет данному условию.

Расширение газа в пустоту – пример необратимого процесса. Его нельзя провести в противоположном направлении.

Источник