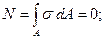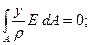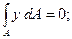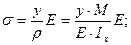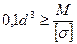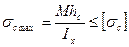Прочность по нормальным напряжениям что это
Техническая механика
Сопротивление материалов
Напряжения при изгибе
Нормальные напряжения при чистом изгибе
Как было установлено ранее, в поперечных сечениях балки при чистом изгибе возникают только нормальные напряжения растяжения и сжатия. Вопрос о распределении этих напряжений по поперечному сечению решается путем рассмотрения деформаций волокон балки.
Из подобия треугольников запишем равенство:
Составим уравнения равновесия:
1. Σ Z = 0; ∫dN = 0, или: ∫σ dA = ∫Еy / ρ dA = Е / ρ ∫y dA = 0 .
где: I = ∫y 2 dA – момент инерции поперечного сечения относительно нейтральной оси; ЕI – жесткость сечения при изгибе.
Так как при чистом изгибе балки постоянного сечения Ми = const, то:
Следовательно, изогнутая ось такой балки представляет собой дугу окружности. Выражение радиуса кривизны подставим в формулу для определения нормальных напряжений; тогда:
Максимальное значение нормальные напряжения будут иметь у волокон, наиболее удаленных от нейтральной оси:
Итак, наибольшие нормальные напряжения при чистом изгибе вычисляются по формуле
Нетрудно заметить, что эта формула по своей структуре аналогична формулам для определения напряжений при растяжении, сжатии, сдвиге и кручении.
Касательные напряжения при изгибе
Эта формула называется формулой Журавского и читается так:
касательные напряжения в поперечном сечении балки равны произведению поперечной силы Q на статический момент S относительно центральной оси части сечения, лежащей выше рассматриваемого слоя волокон, деленному на момент инерции I всего сечения относительно нейтральной оси и на ширину b рассматриваемого слоя волокон.
По формуле Журавского можно вывести зависимости для определения касательных напряжений в балках, имеющих разную форму поперечного сечения (прямоугольную, круглую и т. п.).
Например, для балки круглого сечения формула Журавского в результате преобразований выглядит так:
где Q – поперечная сила, вызывающая изгиб, А – площадь сечения балки.
Большинство балок в конструкциях рассчитывается только по нормальным напряжениям, и только три вида балок проверяют по касательным напряжениям:
Расчеты на прочность при изгибе
Условие на прочность при изгибе заключается в том, что максимальное нормальное напряжение в опасном сечении не должно превышать допускаемое.
Полагая, что гипотеза о не надавливании волокон справедлива не только при чистом, но и при поперечном изгибе, мы можем нормальные напряжения при поперечном изгибе определять по такой же формуле, что и при чистом изгибе, при этом расчетная формула выглядит так:
Ниже приведены моменты сопротивления изгибу для наиболее часто встречающихся сечений:
2. Круглое сечение диаметром d: Wкруг = π d 3 / 32 ≈ 0,1d 3
Расчет балок на прочность по нормальным напряжениям
Лекция №16
Тема: «Изгиб»
Понятие о деформации изгиба
Нормальные напряжения при чистом изгибе
Расчет балок на прочность по нормальным напряжениям
Понятие о деформации изгиба
Искривление оси бруса под действием внешней нагрузки называется изгибом. При изгибе в поперечном сечении возникают изгибающие моменты М, т.е. моменты, плоскость действия которых перпендикулярна плоскости сечения. Если изгибающие моменты являются единственным внутренним усилием, то изгиб называют чистым. Однако в большинстве случаев в сечениях бруса помимо изгибающего момента М возникают и поперечные силы Q. Такой изгиб называют поперечным.
Нормальные напряжения при чистом изгибе
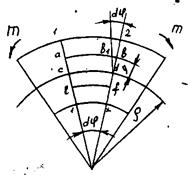
Если на стержень нанести продольные и поперечные линии и подвергнуть его чистому изгибу, то продольные линии изогнутся по дугам окружностей, а поперечные линии 1-1 и 2-2 останутся прямыми, повернувшись на какой-то угол 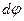
Рис. 1
Из точки d проведем линию, параллельно линии 1-1. Образуемый ее угол с линией 2-2 будет 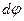
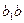
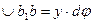
Относительная деформация линии ab будет равна:
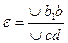
но 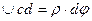
В результате получим:
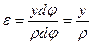
Согласно закона Гука:
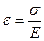
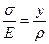
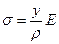
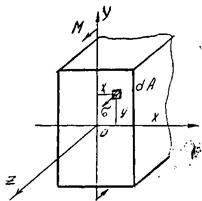
Рис. 2
Установим положение нейтрального слоя, от которого отмеряется расстояние Y. Для этого воспользуемся тем. что равнодействующая элементарных нормальных сил sdA при чистом изгибе должна быть равна нулю:
или подставив формулу (1), получим:
Так как множитель 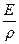
Полученный интеграл представляет собой статический момент сечения Sx. Поскольку он равен нулю, то ось X проходит через центр тяжести сечения.
“При чистом изгибе нейтральная ось проходит через центр тяжести сечения”.
Элементарные силы, возникающие на элементарных площадках dA, будут вызывать элементарные моменты 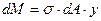
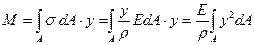
Интеграл, входящий в это выражение представляет собой момент инерции сечения относительно оси X (см. формулу (4), лекция 12):

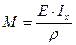
откуда находим кривизну нейтрального слоя:
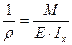
Подставляя это выражение в формулу (1), окончательно получим:
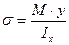
Рис. 3
Из формулы видно, что напряжение прямо пропорционально расстоянию от нейтрального слоя Y. Для точек, находящихся на нейтральном слое, y=0 и x=0. Наибольшие напряжения будут возникать в точках, наиболее удаленных от нейтрального слоя.
Максимальные напряжения будут равны:
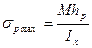
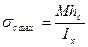
где 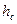
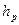
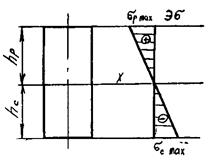
Эпюра напряжений будет иметь вид, показанный на рис. 3.
Если 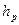
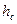
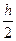
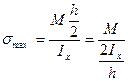
Обозначив 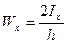
называемый осевым моментом сопротивления, получим:
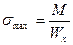
Формула (3) и полученная из нее (6), выведенные при чистом изгибе, применимы и при поперечном изгибе.
Возьмем сумму элементарных моментов 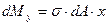
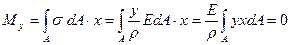
Интеграл 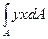
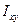
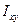
Расчет балок на прочность по нормальным напряжениям
Как уже отмечалось, пластичные материалы имеют одинаковую прочность на растяжение и сжатие. Поэтому профили балок из пластичных материалов делают симметричными относительно центральной оси. Условие прочности для них:
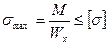
где 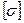
Из условия прочности можно решить следующие три задачи:
1. Проверить на прочность. Прочность обеспечена, если максимальное напряжение меньше или равно допускаемому напряжению.
2. Подобрать сечение. Из условия прочности получим:
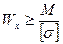
Значения Wx находят по формуле (5).
Для прямоугольного сечения:
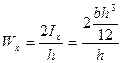
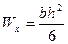
Задавшись высотой или шириной сечения, можно определить второй размер.
Для круглого сечения h=d
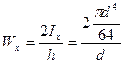
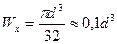
Для двутавра, швеллера и уголков приводятся таблицы (в конце учебников и в справочниках), в которых в зависимости от номера профиля дается значение Wx. По требуемому значению Wx выбирается нужный номер профиля.
3. Определить эксплуатационные способности. Из условия прочности получим:
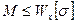
Балки из хрупких материалов изготавливают несимметричными относительно нейтрального слоя, так как хрупкий материал гораздо лучше сопротивляется сжатию, чем растяжению. В этом случае составляют два условия прочности:
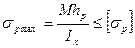
и решают те же три задачи, что и для балки из пластичного материала.
Курсовая, реферат, контрольная – в чем же разница?
Максимальное нормальное напряжение в балке возникает в сечении, где изгибающий момент достигает наибольшей по модулю величины, то есть в опасном сечении
Условие прочности при изгибе формулируется следующим образом: Балка будет прочной, если максимальные нормальные напряжения не превысят допускаемых напряжений
Величина допускаемых напряжений назначается в зависимости от материала, из которого изготовлена балка.
Для хрупких материалов, у которых прочность при сжатии выше, чем при растяжении, допускаемые напряжения на растяжение и сжатие, как правило, не равны между собой и, поэтому, необходимо записывать два условия прочности
Напряжения при поперечном изгибе
Нормальные напряжения, возникающие при поперечном изгибе, с достаточной для практических целей точностью могут определяться по формулам чистого изгиба. Поэтому условия прочности по нормальным напряжениям имеют тот же вид, что и для чистого изгиба.
Касательные напряжения в поперечных сечениях балки появляются при нагружении балки сосредоточенными и распределенными силами. Величина их определяется формулой Журавского:
— статический момент отсеченной части сечения относительно нейтральной оси,
— осевой момент инерции.
Эпюра касательных напряжений показана на рис.6.6.
Условие прочности по касательным напряжениям будет иметь вид:
— статический момент инерции верхней половины сечения.
Полная проверка прочности балки
Эпюра эквивалентных напряжений, построенная для прямоугольного сечения, показана на рис.6.6.
Для обеспечения прочности балки при совместном действии как нормальных, так и касательных напряжений должно выполняться условие
Рациональные формы сечений балок
Рациональным можно считать сечение балки, которое при равной с другими сечениями площади имеет наименьшие напряжения.
Анализируя эпюры напряжений, можно отметить, что на продольной линии нормальные напряжения равны нулю, касательные напряжения достигают максимума, в крайних волокнах, наиболее удаленных от продольной линии, наоборот нормальные напряжения достигают наибольших по модулю значений, а касательные напряжения равны нулю. Расчетная практика показала, что нормальные напряжения, как правило, в несколько раз больше касательных. Поэтому имеет смысл проектировать сечения так, что в зоне действия больших напряжений находилось бы большая часть материала. Этому требованию отвечают сечения в виде двутавровых и швеллеровых прокатных профилей, а также различные коробчатые и кольцевые сечения.
Определение нормальных напряжений при изгибе
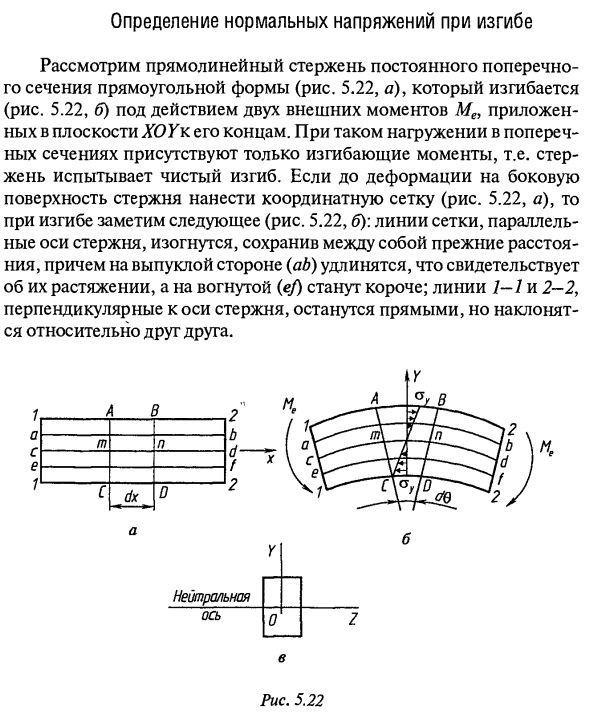


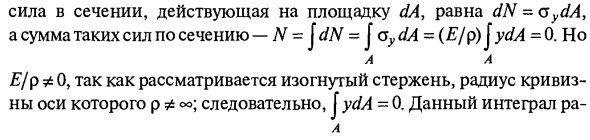

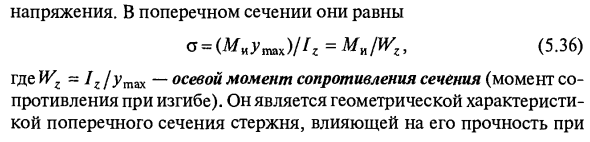


Определение нормальных напряжений при изгибе
Он показывает удлинение и удлинение и становится коротким на вогнутой поверхности (ef). Линии 1-1 и 2-2, перпендикулярные оси стержня, остаются прямыми, но наклонены относительно друг друга. в Рисунок 5.22
Линии сетки, параллельные оси стержня Сохраняя одинаковое расстояние между ними, он может быть согнут на выпуклой стороне (ab). Людмила Фирмаль
Предполагается, что поперечное сечение, которое было плоским до деформации, остается плоским после деформации. При переходе от вытянутой части изогнутого стержня к сжатому стержню возникает слой (а /), в котором во время изгиба не происходит сжатия или растяжения. Это называется нейтральным слоем. Линия пересечения между нейтральным слоем и плоскостью Длина поперечного сечения стержня называется нейтральной осью. Как видите, деформация сердцевины волокна отличается.
Выберите стержневой элемент, окруженный двумя поперечными сечениями на бесконечно малом расстоянии dx друг от друга. При изгибе секции AC и BD будут вращаться под углом Людмила Фирмаль
Вена на статический момент Sz поперечного сечения относительно нейтральной оси (рис. 5.22, в). Поскольку он равен нулю, нейтральная ось (OZ) проходит через центр масс поперечного сечения (см. Раздел 5.11.1). Координата y в уравнении (5.32) получает определенность, она равна расстоянию до оси через центр тяжести сечения. Изгибающий момент сечения L / u = Me. Для заданной рабочей поверхности момента внешней силы Me изгибающий момент равен моменту внутренней силы в той же плоскости.
Против нейтральной оси. Изгибающий момент выражается основной внутренней силой dN. Допустимое направление оси, MPU = 0 и общий изгибающий момент = M »Z = \ ydN = (E / p) J y2dA = (E / p) Iz, (5.33) Где Iz = Jy2dA — момент инерции сечения относительно нейтрали. Ось; p — радиус кривизны искривленного нейтрального слоя. Выразим кривизну нейтрального слоя из уравнения (5.33). 1 / p = МДж (Efz). (5,34) Подстановка этого значения 1 / p в уравнение (5.32) дает зависимость Cy = M pU J11, (5,35) Это позволяет определить нормальное напряжение в любой точке поперечного сечения стержня с известным изгибающим моментом Mn и моментом инерции Iz поперечного сечения относительно оси, проходящей через центр масс поперечного сечения.
Mn max — максимальный изгибающий момент поперечного сечения по длине стержня, и его можно получить из рисунка изгибающего момента Mn = Mi (x). Используйте зависимости при выборе поперечного сечения изогнутого стержня maxadm- Размеры прямоугольного или круглого сечения определяются приведенными выше зависимостями. Для металлических профилей (двутавровая балка, канал, угол и т. Д.) Значение Wz отображается в ассортиментной таблице. Конечный изгибающий момент определяется следующим образом: Л / с
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
7.5. Расчеты на прочность при изгибе по нормальным напряжениям
7.5. РАСЧЕТЫ НА ПРОЧНОСТЬ ПРИ ИЗГИБЕ ПО НОРМАЛЬНЫМ НАПРЯЖЕНИЯМ
Максимальные напряжения в опасном (где действует Mmax) сечении Принимая отношение, получим условие прочности при изгибе σ=≤[σ] где Wz – осевой момент сопротивления сечения. Для прямоугольника Для круга Для кольца, где с = d/D – коэффициент пустотелости. Здесь d – внутренний диаметр полого сечения. Используя условие прочности (7.11), выполняют три вида расчетов. Поверочный. Вычисляют σmax, а затем вычисляют перегрузку или недогрузку в процентах по отношению к допускаемому напряжению, либо находят коэффициент запаса прочности по отношению к пределу текучести для пластичных материалов или пределу прочности для хрупких. Проектный. Из условия прочности (7.11) находят необходимое значение момента сопротивления. Размеры нестандартных сечений (круг, прямоугольник…) округляют в соответствие с ГОСТом. Стандартные прокатные профили выбирают из таблиц сортамента. Если размер сечения выбран меньше требуемого, то выполняют поверочный расчет. Перегрузка более 5 % не допускается. Определение допускаемой нагрузки. При известных характеристиках прочности материала и заданном размере поперечного сечения определяют допускаемое внутреннее усилие (изгибающий момент), а затем, исходя из схемы нагружения, находят допускаемые внешние силовые факторы. Если сечение несимметрично относительно оси z (трапецеидальное, треугольное, тавровое…), а также при использовании хрупкого материала (чугун, керамика…), условие прочности проверяют отдельно по максимальным и минимальным напряжениям, используя формулу (7.9).