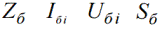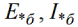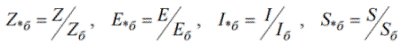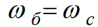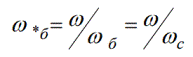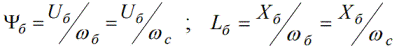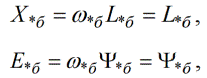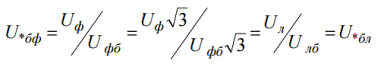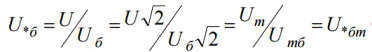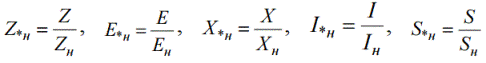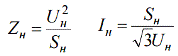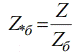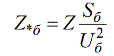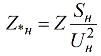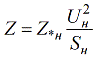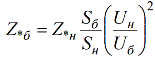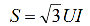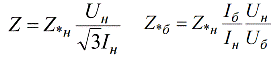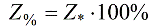Пример измерения чего либо в относительных единицах
§ 1. Атомы. Химические элементы. Относительная атомная масса
1. Приведите примеры трех физических тел, которые: a) состоят из одного вещества; б) состоят из нескольких веществ.
а) Кастрюля, тарелка, линейка (состоят из алюминия).
б) Ножницы, утюг, термометр.
2. Как называются мельчайшие химически неделимые частицы?
3. Расположите следующие объекты в порядке увеличения их размеров: горошина, песчинка, атом кислорода, мячик для настольного тенниса, молекула воды, вишня.
Атом кислорода, молекула воды, песчинка, горошина, вишня, мячик для настольного тенниса.
4. Приведите химические знаки и названия химических элементов, имеющих следующее произношение:
а) плюмбум — Pb — свинец;
б) феррум — Fe — железо;
в) пэ — P — фосфор;
г) купрум — Cu — медь;
д) эн — N — азот;
е) аш — H — водород.
5. Прочтите вслух химические знаки следующих химических элементов и назовите их: Ag, Hg, Zn, S, O, H, Cl, Na.
Ag — аргентум — серебро;
Hg — гидраргирум — ртуть;
Zn — цинк — цинк;
S — эс — сера;
O — о — кислород;
H — аш — водород;
Cl — хлор — хлор;
Na — натрий — натрий.
6. Назовите химический элемент, атом которого имеет самую маленькую массу.
7. Почему химики при проведении расчетов используют относительные атомные массы?
Потому что атомы имеют очень маленькую массу и пользоваться такими величинами масс при проведении расчетов очень неудобно.
8. Приведите пример измерения чего-либо в относительных единицах.
В системе относительных единиц используются единицы мощности и силы тока.
9. Что принято в настоящее время в качестве относительной единицы массы для измерения масс атомов?
В качестве относительной единицы массы для измерения масс атомов в настоящее время используют 1/12 массы атома углерода, которая получила название атомной единицы массы.
Использование относительных единиц при расчете систем электроприводов
При различного рода расчетах нам иногда приходится сталкиваться с таким понятием как относительные единицы или в процентах. Они довольно часто используются при расчетах, где часто нужно проводить сравнение элементов с различными номинальными данными. Давайте рассмотрим что такое относительные единицы на примере системы электропривода.
Не всегда полученные непосредственные результаты могут служить объективным критерием для оценки преимуществ и недостатков сравниваемых вариантов. К примеру анализ пускового тока двигателей постоянного тока с различным номинальным напряжением не сможет дать точный ответ где условия пуска будут легче. Соответственно нельзя сделать заключение о величине пусковых сопротивлений на каждой ступени. Для избежания неопределенности целесообразней проводить расчеты не в абсолютных единицах (Вольты, Амперы и т.д.), а в относительных. Это позволит не проводит переходы от одних единиц к другим, от одних измерений к другим, а с помощью специально построенных кривых определять параметры двигателя непосредственно (необходимые для построения характеристик двигателя).
Чтобы выразить величину в относительных единицах необходимо ее абсолютное значение отнести к аналогичной величине, принятой за единицу.
Выбираться величины могут произвольно, но для систем электроприводов обычно используют номинальные: Uном – напряжение, Iном — ток, Mном — момент, rном – сопротивление обмоток, nном – обороты вала (об/мин).
Для асинхронных и синхронных электродвигателей nо – скорость вращения магнитного потока статора. Если рассматривается двигатель постоянного тока независимого возбуждения, то для данного типа двигателя nо – скорость идеального холостого хода.
Для удобства обозначения параметр в относительных единицах будет обозначаться той же буквой, но с индексом о.е. или для соотношения величины в процентах %.
Напряжение в относительных единицах и процентах:
В асинхронных двигателях различают два напряжения номинальных: 1 – линейное статора, 2 – ЭДС неподвижного ротора.
Ток в о.е. и процентах:
В асинхронных машинах под номинальным роторным сопротивлением понимают сопротивление каждой фазы роторной обмотки (вместе с добавочным сопротивлением, если используется машина с фазным ротором). Полное номинальное сопротивление ротора при соединении обмоток в звезду:
Соотношение для сопротивлений ротора в случае соединения звездой:
Соответственно значение момента электромашины в о.е. и %:
Скорость вращения вала в о.е. и %:
Так как скорость идеального холостого хода стремится к бесконечности в таких машинах постоянного тока как последовательного и смешанного возбуждения, то для расчета скорости в о.е. и % за единицу измерения принимают скорость номинальную двигателя:
Скольжение асинхронных машин может быть выражено тоже через скорость в о.е. и процентах:
Система относительных единиц

Так, относительная величина выражается как множитель базового значения (тока, напряжения, сопротивления, мощности и т. д.), и не зависит, будучи выражена в относительных единицах, от уровня напряжения. В англоязычной литературе относительные единицы обозначаются pu или p.u. (от per-unit system — система относительных единиц).
Например, для однотипных трансформаторов, падение напряжения, импеданс и потери отличаются при разном подаваемом напряжении по абсолютной величине. Но по относительной величине они будут оставаться примерно одинаковыми. Когда расчет произведен, то результаты легко переводятся обратно в системные единицы (в амперы, в вольты, в омы, в ватты и т. д.), поскольку базисные величины, с которыми сравнивали текущие значения, известны изначально.
Как правило, относительные единицы удобны при расчетах передаваемой мощности, но часто бывает, что параметры генераторов моторов и трансформаторов указываются и в относительных единицах, поэтому каждому инженеру следует быть знакомым с концепцией относительных единиц. Единицы мощности, силы тока, напряжения, импеданса, адмиттанса — используются в системе относительных единиц. Мощность и напряжение являются независимыми величинами, это продиктовано свойствами реальных энергосистемам.
Все системные сетевые величины могут быть выражены как множители выбранных базисных значений. Так, если говорить о мощности, то в качестве базисной величины можно выбрать номинальную мощность трансформатора. Бывает, что мощность, полученная в конкретный момент времени в виде относительного значения сильно облегчает вычисления. Базис для напряжения — номинальное напряжение шины и т. д.
Вообще, контекст всегда позволяет понять, о какой относительной величине идет речь, и даже наличие одного и того же символа «pu» в англоязычной литературе не будет вас смущать.
Итак, все системные физические величины являются именованными. Но при переводе их в относительные единицы (по сути — в проценты), характер теоретических выкладок обобщается.
Под относительным значением какой-нибудь физической величины понимается ее отношение к некоторому базовому значению, то есть к значению, выбранному за единицу при данном измерении. Относительная величина обозначается символом звездочки снизу.
Часто при расчетах в качестве базисных величин принимают: базисное сопротивление, базисный ток, базисное напряжение и базисную мощность.
Нижний индекс «б» обозначает, что это базисная величина.
Тогда относительные единицы измерения будут называться относительными базисными:
К примеру, для измерения угловых скоростей, за единицу принимают угловую синхронную скорость, и значит угловая скорость синхронная будет равна угловой скорости базисной.
А произвольная угловая скорость тогда может быть выражена в относительных единицах:
Соответствующим образом в качестве базисных могут быть приняты для потокосцепления и для индуктивности следующие соотношения:
Здесь базисное потокосцепление — потокосцепление, индуцирующее базисное напряжение при базисной угловой скорости.
Так, если синхронная угловая скорость принята за базис, то:
в относительных единицах ЭДС равно потокосцеплению, а индуктивное сопротивление равно индуктивности. Так получается потому, что базисные единицы выбраны соответствующим образом.
Далее рассмотрим в относительных и базисных единицах фазное напряжение:
Легко видеть, что фазное напряжение в относительных базисных единицах оказывается равным линейному относительному базисному напряжению. Аналогичным образом и амплитудное значение напряжения в относительных единицах оказывается равным действующему:
Важно здесь отметить, что и для любого элемента электрической цепи, относительное сопротивление будет равно относительному падению напряжения в условиях номинальной мощности, подаваемой в цепь.
При расчетах токов короткого замыкания, пользуются четырьмя базисными параметрами: ток, напряжение, сопротивление и мощность. Базисные значения напряжения и мощности принимают независимыми, и через них потом выражают базисные сопротивление и ток. Из уравнения мощности трехфазной сети — ток, затем по закону Ома — сопротивление:
Так как базисная величина может быть выбрана произвольно, то одна и та же физическая величина может, при выражении ее в относительных единицах, иметь различные числовые значения. Относительные сопротивления генераторов, двигателей, трансформаторов, задаются поэтому в относительных единицах посредством введения относительных номинальных единиц. Sн — номинальная мощность. Uн — номинальное напряжение. А относительные номинальные величины записываются с нижним индексом «н»:
Для нахождения номинальных сопротивлений и токов применяют стандартные формулы:
Чтобы установить связь между относительными единицами и именованными величинами, сначала выразим связь между относительной базисной и базисной величинами:
Распишем базовое сопротивление через мощность, и подставим:
Так можно перевести именованную величину в относительную базисную.
И аналогичным образом можно установить связь между относительными номинальными единицами и именованными:
Для вычисления сопротивления в именованных единицах при известных относительных номинальных, используют следующую формулу:
Связь между относительными номинальными единицами и относительными базисными единицами устанавливает следующая формула:
При помощи этой формулы относительные номинальные единицы можно перевести в относительные базисные единицы.
В энергосистемах с целью ограничения токов короткого замыкания устанавливают токоограничительные реакторы, по сути — линейные индуктивности. Для них задаются номинальные напряжение и ток, но не мощность.
и преобразовав приведенные выше выражения для относительного номинального и относительного базового сопротивлений, получим:
Могут быть выражены относительные величины и в процентах:
Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!
Подписывайтесь на наш канал в Telegram!
Просто пройдите по ссылке и подключитесь к каналу.
Не пропустите обновления, подпишитесь на наши соцсети:
Система относительных единиц
Важность относительных единиц
Относительные единицы позволяют лучше судить о значении тех или иных величин. Если например, сообщается, что нагрузка генератора составляет P = 15 кВт, то ничего нельзя сказать о том, велика или мала эта нагрузка для данного генератора. Если например, Pн = 10 кВт, то машина сильно перегружена, а если Pн = 10 000 кВт, то нагрузка ничтожна. В тоже время относительное значение мощности (P* = 1,5 для первой машины и P* = 0,0015 для второй) вполне конкретно характеризует значение нагрузки.
Аналогичным образом обстоит дело со значениями сопротивлений различных цепей электрических машин, которые в зависимости от номинальных данных машин изменяются в весьма широких пределах, если выражать их в физических, или абсолютных, единицах. Например, сопротивление цепи якоря Rа в малых машинах постоянного тока составляет десятки омов, а в крупных – тысячные доли ома. В то же время в относительных единицах это сопротивление изменяется в небольших пределах: Rа* = 0,02 – 0,10 (первая цифра относится к машинам мощностью в тысячи киловатт, а вторая – мощностью несколько киловатт). Это вполне естественно, так как все машины постоянного тока проектируются так, чтобы падение напряжение и потери в цепи якоря были относительно малы.
Классификация статистических показателей
Статистический показатель — количественная характеристика социально-экономических явлений и процессов в условиях качественной определенности.
Различают показатель-категорию и конкретный статистический показатель:
Показатель категория определяет содержание статистического показателя, то есть не численное значение определенного показателя, а его элементы: например коэффициент рождаемости, смертности, национального богатства.
Конкретный статистический показатель — это цифровая характеристика изучаемого явления или процесса. Например: численность населения России на данный момент составляет 145 млн.человек.
По форме различают статистические показатели:
По охвату единиц различают индивидуальные и сводные показатели.
Индивидуальные показатели — характеризуют отдельный объект или отдельную единицу совокупности (прибыль фирмы, размер вклада отдельного человека).
Сводные показатели — характеризуют часть совокупности или в всю статистическую совокупность в целом. Их можно получить как объемные и расчетные. Объемные показатели получают путем сложения значений признака отдельных единиц совокупности. Полученная величина называется объемом признака. Расчетные показатели вычисляются по различным формулам и используются при анализе социально-экономических явлений.









Статистические показатели по временному фактору делятся на:
Статистические показатели связаны между собой. Поэтому, чтобы составить целостное представление об изучаемом явлении или процессе, необходимо рассматривать систему показателей.
Относительные величины
Наряду с абсолютными величинами в экономическом анализе и экономической статистике используются также различные относительные величины. Относительные величины представляют собой различные коэффициенты или проценты.
Основное условие правильного расчета относительных величин — сопоставимость сравниваемых величин и наличие реальных связей между изучаемыми явлениями.
По способу получения относительные величины — это всегда всегда величины производные (вторичные).
Они могут быть выражены:
Различают следующие виды относительных статистических величин:
Относительная величина координации
Относительная величина координации показывает, во сколько раз одна часть совокупности больше или меньше другой, принятой за базу сравнения, или сколько процентов от нее составляет, или сколько единиц одной части целого приходится на 1, 10, 100, 1000,…, единиц другой (базисной) части. Например в 1999 г. в России насчитывалось 68,6 млн.мужчин и 77,7 млн.женщин, следовательно, на 1000 мужчин приходилось (77,7/68,6)*1000=1133 женщины. Аналогично можно рассчитать сколько на 10 (100) инженеров приходится техников; число мальчиков, приходящихся на 100 девочек среди новорожденных и др.









Пример: на предприятии работают 100 менеджеров 20 курьеров и 10 руководителей.Решение: ОВК = (100 / 20)*100% = 500%. Менеджеров в 5 раз больше чем курьеров.тоже самое с помощью ОВС (пример 5): ( 77%/15% ) * 100% = 500%
Относительная величина структуры
Пример: на предприятии работают 100 менеджеров 20 курьеров и 10 руководителей. Всего 130 чел.
Сумма всех ОВС должна быть равна 100% или единице.
Относительная величина сравнения
Пример 8: Объем выданных кредитов частным лицам на 1 февраля 2008 г. Сбербанком России составил 520189 млн.руб, по Внешторгбанку — 10915 млн.руб.Решение:ОВС = 520189 / 10915 = 47,7Таким образом, объем выданных кредитов частным лицам Сбербанком России на 1 февраля 2006 г. был выше в 47,7 раза, чем аналогичный показатель Внешторгбанка.
Различие абсолютных, относительных и базисных единиц
В теории электрических машин, а также в других областях электротехники широко пользуются системой относительных единиц, в которой напряжения, токи, мощности и другие величины выражаются в долях некоторых базисных значениях этих величин. В качестве базисных значений в теории электрических машин берут номинальные значения тока, напряжения и т. д. (для многофазных машин переменного тока – фазные значения).
Относительные величины в отличие от абсолютных величин, измеряемых в физических единицах (например, единицах системы СИ), обозначают звездочкой. Тогда относительные значения тока
Относительное значение мощности
Относительные скорости вращения
и относительный момент вращения машины постоянного тока
В качестве базисного, или номинального, значения электрического сопротивления возьмем
которое для генератора равно сопротивлению нагрузки (потребителя) при номинальном режиме работы генератора. Тогда относительное значение сопротивления r будет
Таким образом, относительное значение сопротивления r представляет собой падение напряжение в данном сопротивлении при номинальном токе, отнесенное к номинальному напряжению, или иными словами, относительное падение напряжения при номинальном токе.
Не трудно видеть, что законы Ома, Кирхгофа и другие в их математической форме, а также уравнения напряжений, моментов и других величин можно выражать и записывать также в относительных единицах.