Как собрать кубик рубика 7х7
Как собрать кубик рубика 7х7
Как собрать кубик Рубика 7х7
Если у вас в руках оказался кубик Рубика 7х7х7 и вы не можете его собрать, то эта статья именно для вас. Начнем с того, что собрать кубик Рубика 7х7х7 не сложнее, чем собрать кубика Рубика 5х5х5, но придется потратить больше времени и сил.
Сборку кубика Рубика 7х7х7 можно разделить на 3 основных этапа:
3) Сборка кубика по принципу 3х3х3.
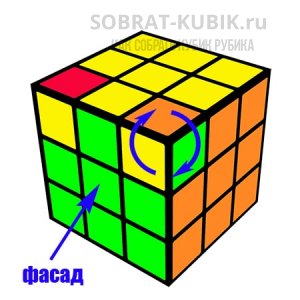
Перед тем, как приступить к самой сборке, необходимо познакомиться с языком вращения
Вращение внешних слоев:
Вращение нескольких внешних слоев:
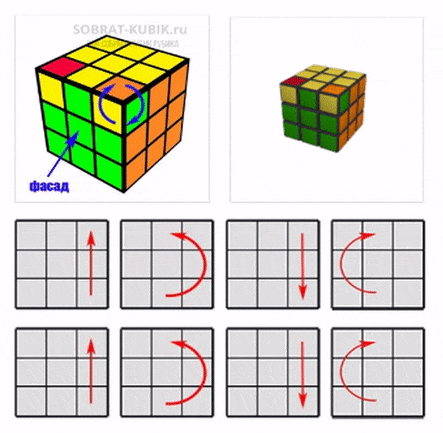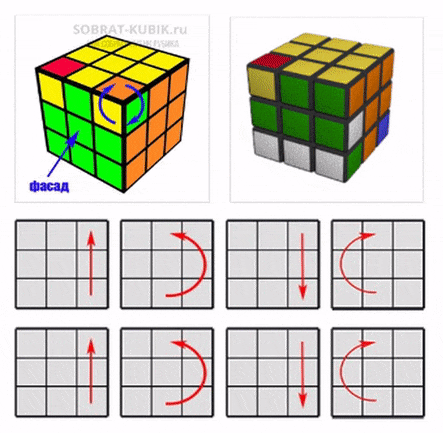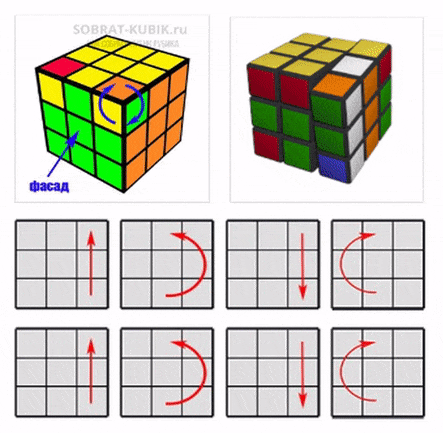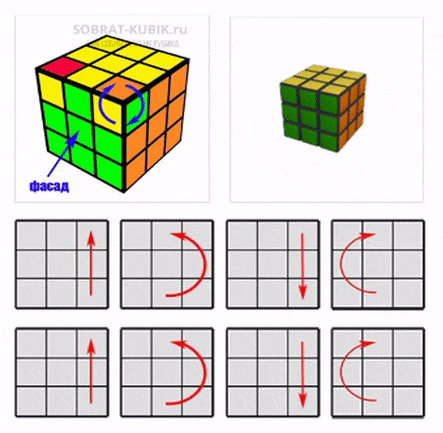
Вращение внутренних слоев
Вращение внутренних слоев происходит аналогично вращению внешних слоев, но вместо прописных букв используются строчные, а также, так как это кубик больших размеров, используются цифры, с указанием слоя по счету с края кубика.
На рисунке показано вращение 3d слоя.
После того, как разобрались с вращением кубика, можно приступать к сборке.
1 этап. Сборка центров
Данный этап делится на несколько небольших подзадач. По классике начнем собирать с белого центра, но если эта идея вам не нравится, то, конечно, можно начать сборку с любого другого цвета, но в этих обучающих материалов мы будем начинать сборку именно с белого цвета.
Сборка белого центра
Первым делом нам нужно собрать центральную полоску из 5 цветов белого цвета, которые находятся по середине. Будет очень хорошо, если у вас получится это сделать на интуитивном уровне, а если так не получается, то попробуйте применить несколько простых советов:
После сборки центральной полоски нужно собрать еще 2 полоски, но уже на 3 и 5 слое. Делать это нужно аккуратно, чтобы не разрушить центральную белую полоску. Лучше всего делать это на других гранях и поднимать к центральной полоске.
Если элемент не встает на нужно место, то нужно отвести его на соседнюю грань (где нет белой центральной полоски), там его развернуть и вернуть на место.
После того, как будет собран блок 3х5, нужно собрать оставшиеся две крайние полоски. Делается это аналогично сборке полос на третьем и пятом слое.
Сборка желтого центра
На рисунке показан пример, как поступить, если осталось загнать последнюю полоску желтого центра, в данном случае n=2, поэтому делаем: 2r’ F2 2r.
Сборка оставшихся центров
Берем кубик таким образом, чтобы белый и желтый центр были справа и слева. Начинать собирать можно с любого цвета, первым делом необходимо найти центральный элемент (а мы не забываем, что центральный элемент нам подсказывает, какого цвета будет центр), собираем центральную полоску, позже собираем остальные полосы.
Самое сложное начинается на моменте сборки последних двух слоев. Важно: собрать максимальное количество элементов по аналогии со сборкой желтого и остальных центров.
На рисунке показан пример, где n=2, m=3. Формула принимает вид: 2R U’ 3l’ U 2R’ U’ 3l.
Для перестановки центральных углов нужно, чтобы на верхней грани “чужой” угол был в правом нижнем углу, а на фронтальной грани “чужой” угол был в правом верхнем углу. Выполняем формулу: 2R U 2R’ U 2R U2 2R’. Для этой ситуации также работает формула из предыдущего пункта.
Первый этап подошел к концу. На кубике должны быть собраны все центры. Если у вас это получилось, то можете переходить к следующему этапу.
2 этап. Сборка ребер
Сборка двух последних ребер
Сборка двух последних ребер выполняется аналогично сборке последних двух ребер на кубике 5х5, но с некоторыми изменениями. Мы делим ребро в кубике 7х7 на два ребра кубика 5х5. Звучит сложно, но на практике все намного проще.
Сначала собираем внутреннее ребро с помощью формул из кубика 5х5, но с заменой: R – 3R, L – 3L. Когда внутренние ребра будут собраны, собираем внешние, также используем формулы из кубика 5х5, но с заменой: R – 2R, L – 2L.
3 этап. Сборка кубика, как 3х3
Поздравляем теперь у вас в руках собранный кубик Рубика 7х7х7!
Интересные факты про кубик Рубика 7х7х7:
Шаг 1 из 7: крест на начальной стороне
Итак, вы уже прочли вводную часть и готовы приступить к сборке «кубика Рубика»!
На этом этапе (шаг 1) самое главное понять принцип сборки кубика, выбрать начальную сторону и собрать на ней крест.
Шаг 1: соберите крест на начальной стороне

Начальная сторона — это сторона, с которой начинается сборка. Когда будет решен первый слой — он будет собран и все цвета на нем совпадут.
Можно выбрать начальную сторону любого цвета. Иногда при выборе начальной стороны (особенно когда собирают на минимальное количество вращений) перед сборкой смотрят, с какого цвета более выгодно начать. В скоростной сборке обычно начинают всегда с одной и той же, например, всегда с белой.
Я обычно, когда решаю «кубик Рубика», начинаю собирать с белой стороны, просто так уже привык, и в среде спидкуберов считается, что с белого цвета начинать выгоднее всего, потому что белый цвет самый яркий и его проще найти глазами на разобранном кубике. На самом деле вам пока совершенно неважно, с какого цвета начинать, я бы даже порекомендовал на первых порах начинать с разных сторон, чтобы сосредоточиться именно на методе, а не на цветах.
Итак, выберите цвет начальной стороны. Первый раз пусть это будет все-таки белый, чтобы вы не запутались с алгоритмами, так как я все рисунки буду приводить для случая, когда начальная сторона именно белая.
Найдите на «кубике Рубика» сторону, где белый центр. Именно там и будет белая сторона.
Как видно на первоначальном рисунке, конечная цель этого шага — собранный белый крест из четырех боковых элементов, содержащих белый цвет. Но не все так просто, нужно еще, чтобы второй цвет каждого белого бокового кусочка совпадал по цвету с центром боковых сторон.

Если никак не получается собрать правильный крест, попробуйте собрать сначала неправильный белый крест, без совпадения боковых наклеек с центрами. Просто белый крест.

Если же не получается собрать крест и без совпадения, тогда вам читайте далее…
Методика собирания креста
Вы спросите, почему же я просто не дал инструкцию сразу, а предложил сначала самим попробовать? Дело в том, что как таковой методики собирания креста не существует! Очень большая степень свободы, если кропотливо ставить кусочек за кусочком, то для этого нужно написать большую методику, и сборка будет медленной. Если же вы смогли додуматься до креста сами, то, скорее всего, вы сами выработаете себе в будущем некую инструкцию в подсознании, которой будете следовать.
Чемпионы по сборке кубика собирают крест так: им дается 15 секунд до сборки (preinspection time), в которые они могут изучить куб и выбрать наиболее выгодное начало. За эти 15 секунд они просчитывают, как будут собирать крест. И, когда начинается сама сборка, на выполнение креста уходит 1,5 — 2 секунды!
Поэтому я приведу не полную методику, а просто различные случаи с их описанием, и как их решать:
Крест состоит из 4-х подвижных боковых элементов, которые нужно собрать вокруг белого центра (белый центр не перемещается). Эти элементы на перемешанном кубике могут находиться где угодно, но в любом случае они боковые, и вы без труда их найдете (боковые элементы, содержащие белый цвет). Теперь приведу примеры, как для разных случаев сделать так, чтобы они встали на свое место.
На этом этапе, на другие элементы кубика, а именно на боковые без белого цвета и любые угловые внимание не обращаем. Нужно собрать именно белый крест и для этого мысленно делим куб на 3 слоя.
Прежде, чем начать собирать крест, посмотрите на сторону, где белый центр, возможно, что рядом с белым центром уже есть боковой элемент с белым, как на рисунке.
В этом случае нам нужно сделать просто поворот верхней грани В, чтобы совпал боковой цвет элемента с боковым центром. Остальные варианты для случая, когда есть белый, аналогичны. Просто поворачиваем верх до тех пор, пока цвет не совпадет
Если на начальной стороне уже два или более боковых элементов с белым, то вращаем верх до тех пор, пока с боковыми центрами не совпадет наибольшее количество элементов.
Теперь перейду к типовым случаям. Здесь важно не запоминать случаи, а именно понять логику процесса, тогда вы все запомните без усилий.
Примеры:
A: элемент находится в первом слое
| Изображение | Алгоритм | Пояснение |
 | П’ В П В’ | Кусочек развернут правильно, но стоит не на своем месте. Сначала надо понять, где «его» место. Его место там, где оранжевый боковой центр. В нашем случае кусочку надо идти в заднюю плоскость, так как напротив красного центра расположен оранжевый. Поэтому делаем алгоритм П’ В П В’. Логика тут такая: опускаем во 2 слой этот кусочек, потом поворачиваем верх так, чтобы его место встало как раз туда, где стоял кусочек, и возвращаем кусочек в верхний слой. Потом делаем движение верхнего слоя обратно, чтобы все встало на свои места. |
 | П’ В’ Ф’ В | Кусочек развернут неправильно, то есть не белым кверху, и его надо переместить в другое место ( в нашем случае к левой плоскости. Делаем так же, как и в предыдущем случае, опускаем этот кусочек во 2-ой слой, потом поворачиваем верх, чтобы при возвращении кусочка, уже развернутым правильно, он попал на свое место. И потом возвращаем верх в исходное положение. |
Б: элемент находится во втором слое
| Изображение | Алгоритм | Пояснение |
 | В2 Ф’ В2 | Здесь все даже проще. Определяем, в какое место креста должен идти элемент. Поворачиваем верх, чтобы его место подошло в тому положению, когда кусочек попадет из 2-го слоя в первый слой и окажется белым кверху, поднимаем кусочек на его место, и возращаем верх обратно. |
 | В П В’ | Зеркально предыдущему случаю, подводим верх, поднимаем кусок, возвращаем верх обратно. |
В: элемент находится в третьем слое
| Изображение | Алгоритм | Пояснение |
 | Н2 З2 | Кусочек с белым и зеленом цветами (белого не видно, он внизу) надо переместить из третьего слоя в первый. В этом случае, когда белый находится в нижней плоскости, переместить его в верхнюю плоскость очень просто, всего лишь надо сдетать двойной, на 180 градусов, поворот боковой плоскости, в которой он находится. Но перед этим мы сначала переведем его туда, откуда он попадет именно в свое место. Вращаем нижнюю плоскость на 180, чтобы он оказался под своим местом, потом заднюю плоскость на 180 градусов. |
 | 1. Н’ Ф’ П Ф 2. П В Ф’ В’ | В этом случае белый кусочек посложнее переместить в верхний слой, потому что он развернут неправильно. |
Как сделать из неправильного креста правильный (чтобы все боковые цвета совпадали с соответствующими центрами)
Вы собрали белый крест и видите, что не все цвета по бокам совпадают. Повращайте верхнюю сторону и смотрите, что совпадает. Как минимум 2 цвета должны совпасть. Когда обнаружили, что два цвета совпадают, а 2 других нет, то, следовательно, нужно поменять 2 других местами.
Возможно всего 2 случая:
| Изображение | Алгоритм | Пояснение |
 | П В П’ В’ П | Алгоритм, меняющий местами два смежных элемента креста |
 | П2 Л2 Н2 П2 Л2 | Алгоритм, меняющий местами два противоположных элемента креста. Альтернативный алгоритм: П’ Л В2 П Л’ В2 |
Научившись собирать крест — разберите опять кубик и попробуйте еще пару раз самостоятельно собрать крест в белом цвете или любом другом цвете, а затем переходите к шагу 2.
3х5х7 Cuboid или пилим Кубик Рубика
Некоторое время назад я увлекся коллекционированием всевозможных головоломок. Я не увлекаюсь спидкубингом и не могу самостоятельно решить бОльшую часть головоломок в своей коллекции. Мне просто нравится пополнять коллекцию чем нибудь интересненьким.
Сначала я покупал всякие кубики Рубика на aliexpress и ebay, но там ассортимент хоть и широкий, но все равно конечный. Но однажды я попал на парочку ютуб каналов (раз, два), где ребята с помощью напильника и такой-то матери изготавливают из 30 лет назад надоевшего всем кубика весьма интересные головоломки. При этом на выходе получается совершенно новая головоломка, требующая совершенно иных подходов к решению. Я тоже начал пилить свои кубики изготавливая различные модификации для своей коллекции.
Однажды ко мне обратилась знакомая с просьбой написать статью как именно я делаю свои кубики. Я как раз собирался делать кубоид 3х5х7 и согласился фотографировать каждый шаг. Правда, статья вскоре оказалось не нужной, но фотки остались. Так что я решил все таки добить начатое.
В статье пошаговая инструкция как делаются подобного рода модификации. Технология в общем-то несложная — посмотрите упомянутые видео и все поймете. Статью можно после этого даже не читать — в ней не будет ничего нового по сравнению с видео 🙂
Итак, вот она заготовка — кубик Shengshou 7x7x7.
Не все кубики подходят для модификаций. Дело в том что часть кубика спиливается и важно, чтобы механизм остался живой. У меня валяется YuXin 7x7x7, который кроме как 7x7x7 ни на что не годится — у него корни некоторых кубиков слишком короткие и велика вероятность отпилить лишнего. Но с этим Shengshou мне повезло, даже не смотря на то, что я купил самый дешевый куб.
Сегодня я буду строить кубоид 3х5х7. Для этого нужно будет банально склеить некоторые части между собой. Чтобы понять что и с чем я буду клеить нарисуем маркером линии на склеиваемых кусочках. За стикеры не переживайте — я их все равно выкину.
Можно разобрать головоломку и клеить кубики по отдельности. Но есть одно но. Во время вращения кубики не прилегают вплотную друг к другу, а находятся немного на расстоянии. Если склеить кубики по отдельности, то эти зазоры исчезнут и кубик будет крутиться хуже. Нужно делать так:
Теперь можно клеить кусочки по отдельности. Раньше мы только скрепили наружные кубики маленькой капелькой клея. Теперь нужно проклеить части более фундаментально.
Я предпочитаю проверять работоспособность механизма на каждом этапе. Для этого можно собрать кубик назад и проверить, что он все еще крутится. Тут я обнаружил несколько криво склеенных кубиков, которые мешали нормальному вращению граней. Кусочки переклеил, все стало крутиться более-менее хорошо.
Кстати, шахматка — отличный способ проверить вращение всех граней и слоев
Теперь можно браться за ножовку. Глубина реза определяется по винту в центральном кубике. Можно сделать выпуклый кубоид, но в этот раз я захотел сделать по форме кирпича параллелепипеда.
Чтобы грани не смещались во время экзекуции я сначала плотно затянул все винты, а кубик туго стянул широким скотчем. Пилил обычной ножовкой по металлу. Можно лобзиком, только не электрическим. На самом деле самый противный этап.
После грубого среза ножовкой всю грань нужно сточить наждачным блоком до более-менее ровной поверхности. Нужно убрать как можно больше высоты, но оставив место для шляпки винта. Шляпку, кстати, тоже можно подточить дремелем, чтобы выиграть еще миллиметр высоты.
Фишка кубоида 3х5х7 в том, что помимо двух спиленных граней у него будет еще 2 нарощенные — ну так он будет лучше смотреться. В ютубе народ наращивает пластинками из ABS пластика, я же напечатал проставки на 3д принтере. Чтобы проставки лучше приклеились соответствующие грани я процарапал ножом.
Проставки — это маленькие брусочки из АБС пластика. Я выбрал высоту около 4мм — примерно столько же я срезал с двух других граней.
Поскольку и проставки и сам кубик сделаны из АБС пластика, то клеить можно обычным ацетоном
Дальше самое интересное, хоть и муторное: все щели нужно заделать. За бугром используют Milliput или Apoxie Sculpt. Я ни того ни другого в глаза не видел, зато в строительном магазине купил штуку по имени Alteco Epo-putty. Позиционируется как холодная сварка, на деле что-то типа двухкомпонентной эпоксидки-пластилина.
Замешиваем, напихиваем во все выемки, на углах лучше налепить с запасом. Штука неплохо растворяется в воде, потому смоченными руками удобно размазывать и заталкивать в щели. Детальку, кстати, тоже стОит смочить водой для лучшей адгезии.
После того как эпоксидка высохла (часов 6) лишнее можно сточить наждачкой. Я использую 180-220 для грубой обточки детали, 400-500 для более гладкой поверхности. Когда деталь готова к покраске дополнительно можно еще пройтись бумагой 800-1200. Для обточки плоских поверхностей удобно бумагу разложить на столе и елозить деталькой по бумаге. В труднодоступных местах можно орудовать надфилем.
Теперь нужно слегка скруглить острые кромки, чтобы головоломка не заедала при вращении. Дополнительно я еще сточил общую внешнюю кромку головоломки довольно большим радиусом (2-3мм). К сожалению у меня не сохранилось фотки этого этапа.
Теперь головоломку нужно покрасить. Я купил акриловую эмаль-аэрозоль в отделе “автотовары”. Лучше было бы глянцевую, но и матовая тоже смотрится неплохо. Ленивые могут красить всю головоломку целиком. Я же предпочел красить все детальки по отдельности.
Финальный штрих — новые наклейки. Практика показывает, что самые лучше наклейки получаются из ПВХ пленки Oracal 641. Я также пробовал пленки других производителей (не всех, буквально 1-2) — к сожалению, не то. У них пленка не глянцевая, тоньше и держится хуже. Единственная отрада — там есть такие цвета, которых нет у Оракала (всякие там флуоресцентные). Покупал в местной компании по декору и рекламным материалам. Они согласились мне нарезать разных цветов пленки по 20см погонных (для кубиков это гигантские объемы — я уже второй год осиливаю куски 20х100см).
Вот и все. Как я уже говорил технология не сложная, но очень муторная. Изготовление одного кубика занимает до месяца по вечерам. Искренне восхищаюсь ребятами, которые делают такое на заказ 🙂
Я показал как из кубика 7х7х7 сделать т.н. кубоид 3х5х7. По той же технологии можно делать еще множество различных головоломок. У меня в коллекции уже есть 4х4х2, 5х5х3, 6х6х4, 7х7х5. Еще едет из китая заготовка для 5х5х7.
Таким же способом можно не только кубики резать. Вот, например, мегамоид (мегаминкс-кубоид).
Аналогичными способом (даже без обпиливания) можно сделать всевозможные бандаж-головоломки (кубики со склеенными кусочками). Я просто в восторге от серии Crazy Planet Cubes и 248 Cube. Достаточно просто склеить кубики и залепить щели эпоксидкой.

Желтая грань сделана методом приклеивания круговых кусочков к квадратным, с последующем заполнением щелей эпоксидкой
На этом на сегодня все. Дайте мне знать если тема головоломок Вам интересна. У меня есть еще заготовки статьи на тему как дизайнить собственные головоломки. Свои разработки я выкладываю на thingiverse — добро пожаловать, качайте, печатайте, предлагайте. Я открыт для конструктивной критики.
Если статья Вам понравилась, Вы можете поддержать меня купив чашечку кофе.
Как собрать кубик Рубика?
П осле публикации рассказа с историей создания кубика Рубика, на блог начали приходить по запросам «как собрать кубик рубика», «схема сборки 3х3» и даже по «тайны кубика рубика для начинающих». Страждущие с горящим взглядом, беспрерывно вращая по пять кубиков в каждой руке, заклинали: «Дайте же! Дайте же нам схему с картинками! Верните нам покой, крепкий сон и здоровое пищеварение!».
К ак ленивый человек, я решил поступить просто: дать желающим желаемое и умыть руки. Так появилась эта страница. Наслаждайтесь.
Схемы сборки кубика Рубика. Для начинающих
Кубик Рубика 2х2: Очень простая инструкция и схема сборки за 3 шага. (PDF, 217 Кб).
В целом, сборка кубика Рубика 2х2 построена на логике сборки последнего слоя кубика Рубика 3х3, поэтому тем, кто справился с 3х3, советы и подсказки, как собрать кубик Рубика 2х2, скорее всего, не понадобятся.
Кубик Рубика 4х4: Схема сборки в три этапа — центральные кубики, боковые кубики, все вместе по аналогии сборки кубика 3х3. (PDF, 897 Кб). Потребуется умение собирать кубик 3х3.
Кубик Рубика 4х4, 5х5, 6х6, 7х7. 11х11: Авторский алгоритм Конищева Г. В., г. Магнитогорск. Универсальный алгоритм, по которому можно собрать кубик Рубика 4х4, 5х5 и больше, вплоть до 11х11. (PDF, 1.8 Мб)
Кубик Рубика 5х5: Схема сборки в четыре этапа — первый слой, затем углы, контур и, наконец, центральные слои. (PDF, 1,4 Мб).
Знаменитые статьи о кубике Рубика, выходившие в популярных журналах во времена СССР:
С татьи из журнала «Наука и Жизнь» о том, как собрать кубик Рубика:
Венгерский Кубик, 1981 г. (PDF, 355 Кб)
А всё-таки, как его собрать?, 1982 г. (PDF, 466 Кб)
Волшебный Кубик 4х4х4, 1983 г. (PDF, 318 Кб)
Молдавская пирамидка, 1985 г. (PDF, 220 Кб)
С татьи из журнала «Квант» о кубике Рубика:
Венгерский волшебный кубик, 1980 г. №12 (PDF, 687 Кб)
Механика волшебного кубика, 1982 г. №3 (PDF, 1,7 Мб)
Алгоритм волшебного кубика, 1982 г. №7 (PDF, 1 Мб)
Кубик в картинках, 1983 г. №9 (PDF, 2 Мб)
С татьи из журнала «Юный Техник» о кубике Рубика:
Всем кубикам кубик, 1982 г. №7 (PDF, 368 Кб)
Снова кубик Рубика, 1983 г. №2 (PDF, 222 Кб)
Другие головоломки на основе кубика Рубика:
МозгоКрут (Rubik’s Brain Racker): Правила игры и задания 3-х уровней сложности (PDF, 353 Кб).
Мозгокрут — это головоломка на основе кубик Рубика и «пятнашек». Выполнена в виде шара.
НЛО Рубика (Rubik’s UFO): Схема сборки (PDF, 403 Кб)
НЛО Рубика — это головоломка по принципу кубика Рубика. Имеет форму диска.
Магия Рубика (Rubik’s Magic): Схема сборки (рисунки) (PDF, 243 Кб)
Магия Рубика (Rubik’s Magic): Буклет на английском языке (PDF, 943 Кб)
Крестики-Нолики Рубика (Rubik’s Tac Toe): Инструкция к игре. (PDF, 184 Кб)
Е сли у вас есть другие варианты алгоритмов сборки кубика Рубика, описания головоломок Рубика или методы их сборки, присылайте их нам и мы опубликуем их на этой странице либо добавим ссылку на ваш сайт.
ТОП-10 мировых рекордов сборки кубика Рубика на скорость:
Поделиться ссылкой на эту страницу в:
Как собрать Кубик Рубика 🤓 🤓
Не стоит переживать, ведь здесь нет никакого обмана. Правда заключается в том, что 99.9% людей не могут собрать Кубик Рубика без подсказки 😉
Мы предлагаем вам самое простое решение. Вам нужно выучить всего 6 алгоритмов!
Прокрутите страницу, чтобы получить больше информации!
Самая простая методика
Мы будем изучить весь процесс поэтапно:
1
Эксперименты
Играйте с кубиком, чтобы привыкнуть к нему. Постарайтесь собрать белую сторону кубика, не используя данное руководство.
2
Обозначения
Запомните буквы, которые используются для обозначения направлений вращения шести сторон кубика, а также подробные описания алгоритмов.
3
Решение
Мы разделяем Кубик Рубика на 7 уровней и собираем каждый из них, не затрагивая ранее собранные блоки.
4
Практика
Оттачивайте движения и запоминайте алгоритмы до тех пор, пока вы не научитесь собирать Кубик Рубика без подсказок.
Откройте для себя Кубик Рубика
Прежде чем приступать к изучению данного руководства, постарайтесь самостоятельно собрать кубик, чтобы привыкнуть к нему и понять, как далеко вы сможете продвинуться без подсказок. Практически каждый человек может собрать одну из сторон кубика, после того, как привыкнет к нему.
Возможно, что вы уже заметили данные особенности:
Фиксированные центральные элементы
Обратите внимание на тот факт, что вне зависимости от ваших движений, центральные элементы всегда остаются на своих местах. Они определяют цвет каждой из сторон кубика.
Грани и углы
Помимо фиксированных центральных элементов, кубик состоит из 8 угловых элементов с 3 наклейками и 12 боковых элементов с 2 наклейками.
Слишком много вариантов
Существует слишком много возможных вариантов сборки кубика (более 43 квинтиллионов), поэтому невозможно правильно собрать кубик, попросту перебирая все возможные комбинации.
Стратегия
Очень трудно не разрушить уже собранные элементы при сборке новых. Нам придется разделить кубик на уровни и использовать отдельные алгоритмы для каждого из этапов, которые позволят сохранить ранее собранные уровни.
Обозначения для Кубика Рубика
Буквы, используемые в алгоритмах
Мы использовали шесть букв для обозначения названий каждой из сторон кубика.
Отдельно указанная буква подразумевает вращение стороны по часовой стрелке, в то время как для вращения стороны против часовой стрелки используется знак апострофа (например, F’).
Вы обрадуетесь, когда узнаете, что в данном руководстве нам понадобятся только буквы F, R, U и L
| U | Поворот верхней грани кубика по часовой стрелке на четверть оборота (90°). |
| F’ | Поворот передней стороны против часовой стрелки. |
| R2 | Поворот правой стороны на пол-оборота. |
Используйте кнопки, чтобы увидеть каждое из действий.
1. Соберите белые грани
Мы приступим к сборке кубика и начнем с белых боковых элементов. Вы можете начать сборку с любого из цветов, однако в данном руководстве мы будем использовать белый цвет для большей наглядности.
Как мы уже знаем, центральные элементы являются фиксированными и они определяют цвет каждой из сторон кубика. Именно поэтому мы начинаем сборку с белых боковых элементов, внимательно отслеживая положение центральных боковых элементов.
Собрать белые грани достаточно просто, ведь нам не нужно следить за большим количеством уже собранных элементов. В большинстве случаев вам придется лишь поворачивать элементы до тех пор, пока они не займут свою позицию.
Мы предлагаем вам несколько примеров, выполнение которых потребует несколько последовательных движений.
U’ R’ U F’
Применяйте этот короткий алгоритм тогда, когда элемент находится в правильной позиции (FU edge), но не на той стороне.
F’ U’ R U
Используйте данный алгоритм в случае, когда вы не можете просто повернуть переднюю грань, потому что она окажется не на той стороне.
U’ R U
Данный алгоритм использует в случаях, когда белый боковой элемент расположен в центральной части на другой стороне.
2. Соберите белые углы
После того, как вы правильно расположили боковые элементы, нам необходимо решить проблему белых углов, чтобы собрать первую белую сторону.
После завершения данного этапа, наш кубик должен выглядеть следующим образом.
На этом этапе вам также не придется запоминать сложные алгоритмы, и вы можете полностью следовать своей интуиции.
Если у вас возникают проблемы на этапе сборки белых углов, вы можете воспользоваться следующим советом. Вам нужно запомнить простой алгоритм, который вы будете повторять до тех пор, пока элемент не окажется на нужном месте:
R’ D’ R D
Переместите угловой элемент в нужное место (Правый верхний угол передней стороны) и повторяйте указанный алгоритм до тех пор, пока элемент не окажется в правильной позиции. Данный алгоритм позволяет перемещать элемент назад и вперед между элементами, отмеченными темным цветом, постоянно изменяя ориентацию в пространстве.
Алгоритм R’ D’ R D работает безотказно, но требует слишком много ненужных движение. Предлагаем вам несколько более коротких алгоритмов:
F D F’
R’ D2 R D R’ D’ R
3. Центральный уровень
Теперь, после того, как мы закончили с белой стороной, давайте перевернем кубик вниз головой, ведь собранная сторона нам больше не понадобится.
Процесс сборки кубика был простым и понятным до этого момента, однако именно данный этап вызывает максимальное количество проблем. Алгоритм, используемый для сборки второй стороны включает в себя большое количество шагов, которые необходимо предусмотреть.
Мы должны запомнить два симметричных алгоритма. Правый алгоритм отправляет боковой элемент из верхней позиции на лицевой стороне в правую позицию на лицевой стороне, в то время как левый алгоритм отправляет элемент в левую позицию на лицевой стороне.
Левый
U’ L’ U L U F U’ F’
Правый
U R U’ R’ U’ F’ U F
В случае, когда у вас нет элемента для перемещения в центральный уровень, вам придется использовать алгоритм дважды, чтобы получить элемент для выполнения первого шага
4. Верхний крест
В ходе четвертого этапа мы должны собрать желтый крест на верхней стороне кубика. Не стоит переживать если цвета боковых элементов не совпадают с цветами центральных. Мы расположим их в нужных местах в ходе следующего этапа.



F R U R’ U’ F’
5. Поменять местами боковые элементы последнего уровня
У нас уже получился крест на верхней стороне, но грани желтых боковых элементов не совпадают с цветами других сторон. Нам необходимо расположить их в правильных позициях.
Для того, чтобы решить данную проблему, мы будем использовать алгоритм, который поменяет местами передний и левый боковые элементы верхней стороны.
R U R’ U R U2 R’ U
В некоторых случаях вам придется поменять местами два противоположных элемента, что потребует разделения данного этапа на два шага.
PВыполните алгоритм один раз и переверните кубик, чтобы удостовериться, что вы меняете местами именно нужные вам элементы.
6. Расположение угловых элементов последнего уровня
Мы практически полностью завершили процесс сборки Кубика Рубика. Осталось лишь правильно расположить желтые угловые элементы. Этот этап состоит из двух шагов. Для начала мы должны правильно расположить их, после чего мы сможем перейти к их ориентированию.
U R U’ L’ U R’ U’ L
Данный алгоритм позволяет перемещать угловые элементы, отмеченные цифрами, в то время как правый верхний элемент на лицевой стороне (отмеченный надписью «ОК») остается на своем месте.
После того, как вы дойдете до данного этапа, внимательно посмотрите и найдите угловой элемент, расположенный в правильной позиции. Если вам удалось найти такой элемент, то именно он будет являться элементом, отсеченным надписью «ОК». Поверните кубик данным элементом к себе и используйте указанный алгоритм. В некоторых случаях вам придется использовать его дважды.
Если вам не удалось найти ни одного элемента в правильной позиции, выполните указанный алгоритм, чтобы перемешать их и найти правильный элемент.
7. Ориентирование угловых элементов последнего уровня
На данном этапе все элементы кубика находятся на своих местах, но желтые элементы сориентированы неправильно. Для того, чтобы завершить сборку кубика, мы будем использовать те же самые алгоритмы, которые применяли для сборки углов первого уровня:
R’ D’ R D
Возьмите кубик в руки и поверните его углом с неправильно сориентированным угловым элементом в куазанную сторону (правый верхний угол лицевой стороны) (как на изображении). Повторяйте алгоритм R’ D’ R D до тех пор, пока данный элемент не окажется правильно сориентирован желтой наклейкой вверх.
Поверните только верхнюю сторону, перемещая другой угловой элемент в указанную позицию и повторите алгоритм R’ D’ R D несколько раз, пока желтая наклейка не окажется на верхней стороне.
Поочередно переместите другие угловые элементы в данную позицию и используйте указанный алгоритм, чтобы правильно расположить желтые угловые элементы.
Вам может показаться, что вы испортили головоломку во время выполнения данного алгоритма, однако это не так, и все вернется на свои места после того, как вы правильно сориентируете желтые угловые элементы.
В примере ниже рассмотрена ситуация, когда все углы сориентированы неправильно. Каждый из элементов перемещается в верхний правый угол на лицевой стороне, после чего алгоритм (R’ D’ R D) выполняется вплоть до момента правильной ориентации элемента.
Нажмите кноаку Воспроизведение, чтобы посмотреть анимированный ролик о действии алгоритма:
Шаг 2 из 7: первый слой
Вы уже собрали крест на начальной стороне и готовы к сборке первого слоя «кубика Рубика»!
На этом этапе (шаг 2) самое главное, это верно собрать первый слой. Именно слой, а не только белую шапку.
Шаг 2: собираем первый слой

Итак, в прошлом шаге 1, вы собрали крест на начальной стороне, теперь переходим к сборке первого слоя. Обратите особое внимание — нужно собрать не только белую шапку, а еще и правильно собрать боковые и угловые элементы.
Первый слой собран неверно, так как угловые элементы не на своих местах.
Первый слой головоломки «кубик «Рубика» собран верно! Как вы наверно заметили, для того чтобы собрать первый слой — нужно поставить на место 4 белых угловых элемента. Всего то!
Начиная с этого момента и до конца сборки всего кубика, мы переворачиваем кубик Рубика первым слоем вниз, то есть держим его так, чтобы первый слой находится внизу, а наверху последняя сторона, в нашем случае желтая и белый крест находится внизу!
Зачем переворачивать кубик «верх дном»?
Все дело в том, что такое расположение куба более выгодно, так как незачем смотреть на то, что уже собрано. Мы теперь смотрим на то, что еще не собрано и как бы отправляем элементы вниз, наращивая собранные слои — вспомните игру «Тетрис» — там тоже применяется тот же принцип. А вот если бы мы держали куб белой стороной вверх — нам постоянно бы приходилось вертеть кубик в руках и смотреть, что внизу. А на это уходит время и есть огромный шанс запутаться во время применения формул.
Поэтому смело поворачивайте ваш «кубик Рубика» собранным начальным крестом вниз и приступайте к решению первого слоя. Просто ищем в верхнем, для нас, слое угловые элемента, которые содержат белый цвет. Верхний слой сейчас можно поворачивать сколько угодно, потому что он никак не может повлиять на собранный внизу белый крест.
Приступаем к сборке

Теперь повернем куб в руках так, чтобы этот совмещенный элемент был сверху-справа-впереди. Белая сторона должна быть всегда внизу, крутите кубик в горизонтальной плоскости.
Теперь возможно всего 3 варианта
| Изображение | Алгоритм | Пояснение |
 | П В П’ | Белый цвет расположен справа. С помощью простого алгоритма убеждаемся, что белый-оранжевый-зеленый угловой элемент встал на свое место. Что и было нужно. Также существуют альтернативные варианты формул: Ф П’ Ф’ П В’ Ф’ В Ф |
 | Ф’ В’ Ф | Белый цвет расположен лицом к нам — данный вариант это зеркальное отражение предыдущего случая. С помощью формулы в три движения, переставляем белый элемент на место. Альтернативные алгоритмы: П’ Ф П Ф’ В П В’ П’ |
 | П В2 П’ В’ ( П В П’ ) | А вот этот вариант — самый длинный случай из трех, так как белый цвет находится сверху. Придется передвигать в два этапа, первая часть алгоритма П В2 П’ В’ нужна для того, чтобы расположить белый не сверху, а сбоку. А потом получаем первый случай, когда белый цвет находится справа и делаем алгоритм П В П’. Также существуют альтернативные решения: П Ф П2 Ф’П’ Ф’ Л’ В2 Л Ф Ф’ П’ Ф2 П Ф |
Что дальше?
Вы поставили один элемент на место, осталось поставить еще три. Для этого опять посмотрим на верхнюю сторону и опять ищем угловой элемент с белым цветом, опять размещаем его над своим местом (цвета совпали с центрами боковых сторон), размещаем куб так, чтобы элемент был сверху-справа-спереди, и делаем один из трех алгоритмов. И так далее, пока не соберется первый слой.
Может возникнуть ситуация, когда в верхнем слое не окажется угловых элементов с белым цветом, они будут в нижнем слое, но стоять не на своих местах. Вам нужно будет вывести неправильно стоящие угловые элементы из нижнего слоя в верхний — для этого расположите ваш куб так, чтобы этот элемент нижнего слоя, который надо поднять наверх, был справа снизу и делаете алгоритм П В П’ или алгоритм Ф’ В’ Ф.
Получилось собрать первый слой? Если да — переходите к следующему шагу 3, в котором вы будете собирать второй слой. Если вы видите, что у вас не получилось — перекрутите кубик и начните собирать заново.
Первый и второй шаг сборки, после которых у вас будет собран первый слой, должна занять у вас минимальное время. Тренируйтесь!
Удивительная математика внутри кубика Рубика
В прошлом году исполнилось 40 лет с того времени, как человечество узнало о кубике Рубика. Эта головоломка сразу смутила умы почти полумиллиарда энтузиастов, которые полагали, что могут раскрыть сумасшедшие секреты этого удивительного кубика, если разберут его на составные части.
В преддверии юбилея кубика Рубика (да, юбилея!) и стартов новых потоков курсов Математика для Data Science и его расширенной версии Математика и Machine Learning для Data Science, пришло время раз и навсегда разгадать эту головоломку, на этот раз с помощью довольно сложной математики. Физические внутренности кубика могут быть изготовлены из пластика, но его виртуальными внутренностями, конечно же, являются числа. Давайте же окунёмся в этот мир чисел.
Разбор кубика Рубика на блоки
Начнем с базовых знаний. Кубик Рубика размером 3x3x3 имеет шесть граней, каждая своего цвета. Центральный кубик каждой грани прикреплён к внутренней крестовине, скрепляющей все элементы куба. Центральные кубики могут только вращаться вокруг своей оси. Одни и те же цвета всегда располагаются напротив друг друга; на стандартном кубе белый цвет находится напротив жёлтого, красный – напротив оранжевого, синий – напротив зелёного.
Если разобрать кубик Рубика, можно увидеть, что он состоит из трёх типов составных блоков. Первый тип: центральная крестовина, на которой удерживаются центральные кубики каждой грани. Второй тип – маленькие кубики размером 1x1x1. Угловые кубики имеют три цветные стороны, бортовые кубики – две. Кубик Рубика имеет одну крестовину, восемь угловых кубиков и двенадцать бортовых кубиков.
С помощью математики мы можем узнать общее количество способов, которыми можно перемешать кубик Рубика: 43 252 003 274 489 856 000. В виде математической формулы это число можно представить следующим образом: (3 8 8!)(2 12 12!)/12. Вот как получается эта формула.
Далее учитываем перемещения каждого углового кубика. Всего угловых пазов восемь, поэтому у первого углового кубика есть восемь вариантов. У второго углового кубика остается семь вариантов, у следующего слева кубика – шесть вариантов и так далее, вплоть до последнего углового кубика, который должен войти в последний угловой паз. Это даёт факториал 8!.
Таким образом, первая часть формулы (3 8 8!) осуществляет подсчёт всех способов, которыми угловые кубики могут размещаться в кубе. Значение 3 8 – это их ориентация, а 8! – их положение.
В следующей части формулы (2 12 12!) применяется тот же принцип, но теперь для ребер. Рёбра имеют только две ориентации, поэтому 12 рёбер могут иметь в общей сложности 2 12 ориентаций. Всего имеется 12 положений, поэтому 12! представляет собой количество способов, которыми кубики могут быть размещены в таких положениях.
Что ещё осталось в формуле (3 8 8!)(2 12 12!)/12? Осталось деление на 12. Деление на 12 связано с одной особенностью кубика Рубика, о которой многим известно, но которую не до конца её понимают. Проведём мысленный эксперимент (который, возможно, вы уже проводили вживую!):
Предположим, вы разобрали кубик Рубика, вытащили из него все кубики, а затем вставили все кубики обратно в случайные пазы (при этом угловые кубики можно установить только в углы, а бортовые кубики – только на рёбра). Вы получите конструкцию, которая выглядит как обычный перемешанный кубик, и на данный момент мы подсчитали все возможные комбинации созданного таким образом куба: (3 8 8!)(2 12 12!). Теперь зададим вопрос, всегда ли можно собрать такой перемешанный кубик, не разбирая его на части?
Здесь кроется ловушка, в которую попадало множество начинающих любителей разгадывать эту головоломку. Если вы тренируетесь и хотите перемешать уже собранный куб, необходимо сохранить куб в целости и собрать его вручную. Если разобрать куб на части и собрать кубики случайным образом, вероятность того, что головоломку можно будет решить, составит всего 1 к 12.
Ответ кроется в алгоритмах
Хотите понять, почему вероятность составит всего 1 к 12? Есть хороший визуальный способ понять, почему вероятность именно такая. Шанс собрать разобранный на составные кубики и снова случайным образом перемешанный большой куб будет равен шансам собрать куб со следующими образцами граней:

Мы разместили их таким образом, чтобы было понятно, как получается коэффициент 12. Ряд 1 имеет нормальные углы. У рядов 2 и 3 один угол повёрнут. Столбец 1 имеет нормальные рёбра. У столбцов 2 и 3 одно ребро повёрнуто. У столбца 3 два ребра поменяны местами. И, наконец, в столбце 4 одно ребро повёрнуто и два ребра поменяны местами.
Таким образом, 12 кубов, представленных выше на фотографиях, не могут быть преобразованы друг в друга. 13-го варианта, который нельзя преобразовать ни в один из таких 12 кубов, не существует. Откуда нам это может быть известно?
Между тем, что может и что не может быть сделано посредством перемещения граней куба, есть связь. Последовательность перемещений граней куба энтузиасты сборки часто называют «алгоритмом». Популярными алгоритмами являются те, которые перемещают лишь несколько кубиков, оставляя остальные нетронутыми. Число 12 возникло по той причине, что на такие алгоритмы накладываются ограничения.
Число 12 составляется из трёх множителей: 12 = 3 * 2 * 2. Откуда берутся множитель 3 и два множителя 2?
Множитель 3: существует алгоритм, который поворачивает каждый из двух разных углов, но нет алгоритма, который поворачивает один угол (оставляя все остальные нетронутыми). Другими словами, если взять обычный кубик Рубика, вынуть один из его углов и заменить его на повёрнутый, такой куб собрать будет невозможно, то есть вы переместитесь из верхнего левого угла нашей диаграммы в одну из клеток прямо под ним.
Однако, если повторить эту операцию и повёрнуть еще один угол, второй множитель 3 не добавится. Теперь, когда в кубе повёрнуто два угла, мы можем последовательно применять алгоритм, поворачивающий два угла, до тех пор, пока не зафиксируется по крайней мере один из углов. Если другой угол случайно встанет на своё место, можем считать, что нам повезло и такой куб можно собрать. Ориентация углов может быть троякой.
Рассуждения относительно первого множителя 2 аналогичны. Существует алгоритм, поворачивающий на свое место каждое из двух разных рёбер, но алгоритма, способного повернуть на своё место только одно ребро, не существует. Таким образом, любое количество повёрнутых ребер может быть сведено к одному ребру, которое в итоге либо окажется, либо не окажется повёрнутым – варианта всего два.
Последний множитель 2 фактически относится к граням и углам, хотя на диаграмме мы показали его с гранями. Существует алгоритм, меняющий местами два угла, одновременно меняя местами два ребра. Но нет ни одного алгоритма, который был бы способен менять местами ни только пару углов, ни только пару рёбер.
Возьмите куб, вытащите два ребра и поменяйте их местами – на диаграмме вы попадёте на столбец, расположенный либо между столбцами 1 и 3, либо между столбцами 2 и 4. Аналогичные рассуждения можно применить, если поменять местами пару углов. Однако перемена местами пары ребер и пары углов уравновешивает баланс, так как алгоритм выхода из таких состояний существует.
Итак, после того как мы объяснили, откуда взялись все множители в коэффициенте 12, можно понять, откуда взялась формула (3 8 8!)(2 12 12!)/12. Число всех возможных положений кубиков в кубе составляет (3 8 8!)(2 12 12!), но только двенадцатая часть таких положений годится для сборки куба. Таким образом, число (3 8 8!)(2 12 12!)/12 обозначает количество способов, которыми можно перемешать кубик Рубика, не разбирая его на части.
Доказательство Популярной механики
Если вы достаточно любопытны, то, наверное, захотите проверить, верны ли сделанные выше утверждения. Существуют ли более сложные математические приемы, которые могут доказать, что «алгоритма, способного повернуть на своё место только один бортовой кубик, не поворачивая любой другой кубик, не существует»? Да, такие математические приёмы существуют. Вот как примерно строится такое математическое доказательство:
При переворачивании грани куба происходит перемещение четырёх бортовых кубиков. Рассмотрим, к примеру, алгоритм из 10 перемещений. Для каждого кубика выполните алгоритм и посчитайте, сколько раз перемещался кубик, и назовите это количество «числом перемещений кубика». Сложите эти числа для каждого бортового кубика, всего должно получиться 40 перемещений кубиков, так как каждое из 10 перемещений добавляет к сумме четверку.
В общем случае для любого алгоритма общее число перемещений бортовых кубиков должно быть кратно 4. Теперь пара важных фактов: если бортовой кубик перемещать чётное количество раз и вернуть его обратно в тот же самый паз, он будет иметь такую же ориентацию. И наоборот, если бортовой кубик перемещать нечётное количество раз и вернуть его обратно в тот же самый паз, он будет иметь перевёрнутую ориентацию.
Естественно, сказанное выше можно доказать с использованием более сложных математических методов, но мы не собираемся сильно углубляться в математику, иначе объём данной статьи превзойдёт все мыслимые и немыслимые пределы. Эти два факта также можно проверить экспериментально, чтобы понять, что всё происходит именно так. (В этом доказательстве поворот на 180 градусов считается двумя перемещениями каждого соответствующего кубика.)
Теперь давайте рассмотрим гипотетический алгоритм, достигающий цели, поворачивающий один бортовой кубик, оставляя при этом в неприкосновенности другой кубик. Одно повёрнутое ребро было перемещено алгоритмом нечётное количество раз, а каждое из 11 остальных рёбер было перемещено чётное количество раз. Сумма 11 чётных чисел и одного нечётного числа всегда нечётна, но мы показали ранее, что такая сумма должна быть кратна 4. Может ли нечётное число быть кратно 4? Нет, не может. Следовательно, такого алгоритма не существует.
Теперь вы понимаете, что число (3 8 8!)(2 12 12!)/12 представляет собой количество возможных состояний куба. Но для изучающего куб математика это лишь предварительная информация. Перед тем как начинать применять более сложные математические методы, задайте себе главный вопрос: «Существуют ли в этой теме математические вопросы, оставшиеся без ответов?»
Число Бога и многое другое
Главной задачей, поставленной изобретателем головоломки, естественно, была сборка куба. Эрно Рубик (Ernő Rubik) создал первый прототип головоломки в 1974 году, и через шесть лет она поступила в массовую продажу. Естественно, он был первым, которому удалось собрать куб.
В 1980 году кубик Рубика стал хитом продаж в магазинах игрушек. Но некоторые математики уже несколько лет экспериментировали с его ранними версиями. Одним из них был доктор Дэвид Сингмастер (David Singmaster) – составитель знаменитого путеводителя «Записки о Волшебном кубике Рубика» и разработавший нотацию для записи операций поворота граней куба. Эта нотация стала стандартом и теперь известна как нотация Сингмастера.
Если бы это была статья писалась в 1980-х годах, то, возможно, стоило бы подробнее объяснить читателям, что такое нотация Сингмастера, и использовать её при описании алгоритмов сборки куба. Множество авторов статей так и делали. Но сегодня на Youtube выложено множество видеоинструкций, поэтому в этой статье мы не будем отвлекаться на описание нотации.
За последние несколько десятилетий рекорд сборки кубика Рубика на время постоянно обновлялся. На сегодня мировой рекорд сборки кубика Рубика человеком составляет 3,47 секунды. В 1997 году доктор Джессика Фридрих разработала самый известный, самый скоростной и самый гибкий метод быстрой сборки кубика Рубика Самые быстрые сборщики кубика Рубика сегодня пользуются разными вариантами сборки от доктора Фридрих.
По мере того как одни пользователи оттачивали мастерство сборки, другие пытались решать важные математические вопросы, связанные с этой головоломкой. За сколько ходов можно собрать куб независимо от того, в каком состоянии он первоначально находился? Если кто-то перемешал куб за 500 ходов, то, естественно, собрать его можно менее чем за 500 ходов. На насколько именно меньше ходов?
Соответственно, была поставлена главная математическая задача: существует ли магическое число, позволяющее сказать: «любой перемешанный куб может быть собран именно за такое количество ходов [или меньше]»? Благодаря остроумному замечанию, что для обретения чувства уверенности нужно божественное вмешательство, это число получило название «Число Бога».
Первая гипотеза о существовании Числа Бога была выдвинута доктором Морвеном Тистлетвэйтом (Morwen Thistlethwaite) в 1981 году, который доказал, что это число существует и не превышает 52. Другими словами, любой перемешанный куб может быть собран за 52 хода или меньше.
В 1990–2000-х годах математики пошли ещё дальше. В июне 2010 года группа из четырёх учёных доказала, что Число Бога равняется 20. На этом веб-сайте, который ведут эти учёные, представлены самые последние знания о кубике Рубика.
Другими словами, какое бы хаотичное первоначальное состояние ни имел Кубик Рубика, его всегда можно собрать за 20 или менее ходов.
Для математиков в теме кубика Рубика остались лишь небольшие лакомые кусочки. Число Бога определено и равняется 20. Но точно неизвестно, сколько именно из 43 252 003 274 489 856 000 комбинаций потребуют для сборки полных 20 ходов.
Количество комбинаций, для сборки которых требуется ровно один ход, составляет 18. Это значение легко рассчитать. Есть шесть граней и три способа поворота каждой из них. Сколько кубов можно собрать ровно за два или три хода? Для математиков эта задача сложности не представляет, но можно предположить, что с увеличением количества ходов также будет увеличиваться сложность вычислений. Сегодня математики уже добрались до числа ходов 15; мы точно знаем количество комбинаций, для сборки которых требуется ровно 15 ходов, но пока не вполне точно представляем количество комбинаций для числа ходов от 16 до 20.
И это – последняя нерешённая задача в математической теме кубика Рубика. Будем ждать, когда кто-либо её решит. Может быть, это будете вы?
Получите нужные знания и навыки на курсе Математика для Data Science и его расширенной версии Математика и Machine Learning для Data Science. А промокод HABR даст скидку 50%.
Узнайте, как прокачаться в других специальностях или освоить их с нуля:
Как собрать кубик 7х7 Часть 18 (Последний этап сборки)
Евгений Кулаков Life
Как собрать кубик 7х7 Часть 18 (Последний этап сборки). В этом видео вы узнаете о последнем этапе в сборке кубика 7х7, он заключается в сборке куба точно так же как и 3х3! Канал EAC.TV на YouTube: 🤍🤍youtube.com/channel/UCMSqRVYwtLB5lr_vZO5qZhg Группа EAC.TV Вконтакте: 🤍vk.com/public122457788 EAC.TV на Drive2: 🤍🤍drive2.ru/users/eac-tv/ Ведущий,Механик,Автоинструктор Евгений Вконтакте: 🤍vk.com/id97510569 Инстаграм Евгения: 🤍🤍instagram.com/evgeniy.kulakov.1995/
Про ребра надо говорить в одной части а то растянул
Евгений Кулаков вы сказали что Фридрих не льзя использовать на кубике 7 на 7 а сами вы делаете f2l
Спасибо большое, я собрал с твоей огромной помощью.
Найс последнее не чего не понял
Спасибо. Буду учить формулы и научусь собирать. Подписка не глядя.
Я посмотрел все этапы и все сделал до того как ты говоришь что надо сделать 2 ушка и 2 глазка у меня выходит так что только 2 ушка. Скажи из что делать
сяб, благодаря тебе собрал)
Ты лучше всех объяснил как собрать семерку!
Все было отлично,только вот этот последний видос,как мне кажется халтурно сделано,без формул и не понятно,объясняешь нам как начинающим,а потом говоришь что решаешь вот эту проблему каким то олл или что-то типо того, сделай пожалуйста поподробнее концовку
Как собрать кубик 7х7 Часть 18 (Последний этап сборки). В этом видео вы узнаете о последнем этапе в сборке кубика 7х7, он заключается в сборке куба точно так же как и 3х3!
В предыдущих частях нашей пошаговой инструкции для новичков, вы должны были собрать:
Как собрать желтую сторону кубика Рубика 3х3
А теперь перейдем к последней схеме и алгоритму её применения.
Как собрать последнюю сторону кубика Рубика 3 на 3
Во время сборки последней стороны головоломки 3х3, вы может столкнуться с ситуациями:
На рисунках выше, изображены две возможные ситуации при сборке последнего слоя кубика Рубика 3х3.
Для решения любой из ситуаций, Вам понадобится всего одна формула. Нюанс в том, что ее нужно повторять несколько раз.
Если у Вас еще нет хорошего кубика, купить современный скоростной кубик 3х3 можно по у наших друзей и партнеров ссылке: https://cubes.in.ua/ kubik-rubika-3×3/
Как собрать последний угол кубика Рубика 3х3
Действие формулы, при помощи которой вы будете поворачивать уголки на последнем слое, показаны на рисунке ниже.
Формула поворачивает по часовой стрелке, правый-верхний-ближний угловой элемент головоломки. Как показано на рисунке ниже.
Кубик Рубика поворот углов
Для вращение угла кубика Рубика, возьмите куб так, чтобы уголок который надо повернуть, был справа вверху, как показано на рисунке.
И проделайте схему нужное количество раз!
На иллюстрации изображено как нужно держать кубик
Рубика во время проделывания алгоритма по вращению угла.
Формула состоит из восьми движений. Но проделать ее надо 3 раза!
Так как, за восемь действий, данная схема поворачивает уголок кубика на 1/3 полного оборота, вам необходимо:
Именно такая ситуация показана на анимационной картинке ниже, для ситуации с рядом стоящими уголками.
Тут главное не запутаться, и не повернуть кубик в руках.
Вам нужно запомнить, что данная схема делается три раза!
Если вы сделаете ее один, или два раза, все ваши труды предыдущих этапов пойдут насмарку, и Вам придется начинать сборку с самого начала нашей поэтапной инструкции.
Пишите отзывы и комментарии ниже, о том с какого раза у Вас получилось собрать кубик Рубика 3х3 по нашей инструкции для начинающих куберов.
Как собрать кубик рубика
Кто хотя бы раз не пробовал собрать кубик рубика? На первый взгляд, задание кажется простым – собрать все грани по цветам. Но на деле оказывается, что выполнить это не так просто. Всему виной то, что кубик рубика – это математическая головоломка. Чтобы ее решить, придется воспользоваться специальными правилами.
Интересно, что этот магический кубик завоевал сердца не только детей, но и миллионов взрослых. Сегодня во всем мире насчитывается около 500 миллионов экземпляров.
Важно! Если вдруг вы уронили кубик рубика и он рассыпался, не торопитесь быстро его собирать. Важно правильное расположение цветов. В ином случае, ошибочное расположение граней приведет к тому, что кубик рубика невозможно будет собрать. Не стоит пренебрегать этим фактором.
Как собрать кубик рубика для начинающих
1 этап. Про Новый год говорят, как начнешь его, так и проведешь. С кубиком рубика также. От того, как начать его собирать, зависит: соберем его в конечном итоге или нет.
Одна из популярных техник – «Ромашка». Когда у вас центр(серединка), например, синего цвета, а 4 грани — лепестки зеленого цвета. Но будьте внимательны, чтобы цветы были строго противоположных граней. Например, белый и желтый или красный и оранжевый. Другие варианты будут некорректны. Собираем на верхней поверхности кубика.
Как собрать. Серединку выбрать просто – любая, которая нравится. А с лепестками сложнее. Есть 5 вариантов:
1.Когда нам нужно просто поднять правое или левое ребро вверх.
2.Ребро нужно поднять вверх 2 раза.
3.Мы видим, что синий «лепесток» смотрит на нас, но если мы его поднимем вверх, то уйдет тот, который уже стоит на месте. Тем не менее, с других сторон «лепестков» нет. В таком случае мы поворачиваем верхний фронт до тех пор, пока нужное «место» не совпадет со стороной «лепестка». И поднимаем наш «лепесток». Итого: ставим место, ставим «лепесток».
4.Нужный цвет смотрит на нас, но если мы его поднимем – то все сместится. Для этого делаем движение «Фронт» — поворочаем нашу грань, которая смотрит на нас, вправо (или влево). Получается вариант №3. Делаем аналогично.
5.Бывает, что «лепесток» внизу и смотрит на нас. Делаем «Фронт». Подставляем наш элемент. А затем возвращаем прошлый на то место, где стоял до этого «лепесток».
2 этап. Теперь выбираем любую боковую грань. Например, с красным центром. Делаем так, чтобы квадратик посередине в верхнем фронте (строке) стал тоже красным. И поворачиваем нашу грань два раза вправо или влево, чтобы она опустилась вниз. То же самое проделываем с оставшимися 3 боковыми гранями. Если все сделать правильно, то на нижней стороне кубика получится правильный зеленый крест.
3 этап. Ищем углы, где еще есть зеленый цвет. Нашли один. Его соседи – красный и желтый. Зеленый запомнили и пока оставили. Ищем красный и желтый центры. Место этого уголка будет там, где находятся эти центры. Ставим максимально близко наш уголок к его правильному месту. Теперь крутим формулу «Пиф-Паф».
Волшебная формула «Пиф-паф». Вверх – влево – вниз – вправо. Для этого правый столбик мы проворачиваем вверх. Затем верхний фронт (верхняя строка) проворачиваем влево. Правый столбик вниз. И верхний фронт вправо. Если повторить ее 6 раз, то кубик снова соберется. Она вам еще не раз поможет в сложных ситуациях.
Делаем ее пока уголок не встанет на свое место. Точно также проделываем с другими уголками. Иногда можно не заканчивать формулу до конца, если это нужно. Обратите внимание, что в уголках должны совпадать все цвета с центрами граней. У нас собрана не только зеленая грань, но и первый слой по цветам. Если уголки стоят не на своих местах (не совпадают с цветом граней), то мы снова делаем формулу «Пиф-паф».
4 этап. Здесь нам пригодится формула «Пиф-паф» только для левого столбика. И звучать она будет «вверх – вправо – вниз – влево». Сейчас работаем с ребрами, где нет синего цвета. Т.к. он отвечает за третий слой. А мы еще на втором. Смотрим на любое ребро. Видим, например, что на нем 2 цвета оранжевый и желтый. Ищем желтый центр. Если он справа, то делаем правый «пиф-паф». Если слева, то левый. Повторяем так со всеми гранями.
5 этап. Собираем третий слой. Существует 2 основных варианта развития событий.
1.В центре образовалась прямая синяя линия (или любой другой цвет). Важно держать кубик в руках так, чтобы она была вверху горизонтально. Делаем «фронт» — поворачиваем грань, которая смотрит на нас, один раз вправо. И делаем правый «Пиф-паф». Затем «фронт» обратно – поворот влево один раз. Получается крест из синего цвета.
2.У нас полкреста: центр и 2 ребра – лепестка. Держим кубик в руках так, чтобы наши полкреста напоминали расположение стрелок часов на 9 вечера. Делаем фронт вправо, правый «Пиф-паф» и фронт обратно. Повторяем формулу еще раз. Получается синий крест.
6 этап. Достраиваем элементы с помощью формулы «вверх – влево – вниз – влево – вверх –вправо – вправо – вниз – влево». Меняем уголки с помощью формулы «Пиф-паф».
7 этап. Таким образом, мы смогли собрать кубик рубика 3*3.
Как собрать кубик рубика 2 на 2 для детей
Вам помогут 3 простые техники.
Техника№1. Поворачиваем стороны «вниз (правый столбик) – влево (нижний фронт) – вверх (правый столбик)»
Техника№2. Поворачиваем грань, которая смотрит на нас, один раз вправо. Нижний фронт тоже вправо. Затем грань, которая смотрит на нас, влево.
Техника№3. Поворачиваем грани «вниз (правый столбик) – 2 раза вправо (нижний фронт) – вверх (правый столбик – вправо (нижний фронт) – вниз (правый столбик) – влево (нижний фронт) – вверх (правый столбик)». Симметрично можно проделать то же самое только с левым столбиком.
Как собрать кубик рубика 4 на 4
1.Собираем квадраты 2 на 2 на каждой стороне кубика.
2.Парами располагаем ячейки других цветов около ребер.
3.Собираем также, как кубик 3 на 3.
Как собрать кубик рубика 5 на 5
Его не так сложно собрать, как кажется на первый взгляд. Цвета сторон уже определены, сама конструкция очень схожа с кубиком 3 на 3. Поэтому собираем аналогично. Единственное отличие заключается в том, что собираем не по слоям, а от центра к краям. Когда мы вращаем внешние грани, внутренние остаются на месте. Затем остается справиться с углами и готово!
Как собрать кубик рубика поэтапно. Шпаргалка
План, которого стоит придерживаться, при сборке кубика рубика 3 на 3.
1.Собираем крест (можно с помощью «ромашки»).
2.Следим, чтобы он был правильный.
3.Выстраиваем второй слой с помощью техники «Пиф-паф».
Источники информации:
- http://soberi-kubik-rubika.ru/step1/
- http://habr.com/ru/post/408607/
- http://www.seoded.ru/articles/how-to-assemble-a-rubiks-cube.html
- http://cubesolve.com/%D0%BA%D0%B0%D0%BA-%D1%81%D0%BE%D0%B1%D1%80%D0%B0%D1%82%D1%8C-%D0%BA%D1%83%D0%B1%D0%B8%D0%BA-%D1%80%D1%83%D0%B1%D0%B8%D0%BA%D0%B0/
- http://soberi-kubik-rubika.ru/step2/
- http://habr.com/ru/company/skillfactory/blog/546094/
- http://raiero.ru/kak-sobrat-kubik-7h7-chast-18-posledniy-etap-sborki-xl-xf0g0ujD5HHVK7omn4t-vi.html
- http://sobrat-kubik.ru/sborka-3×3/7-sobrat-posledniy-sloy.html
- http://7days.ru/lifestyle/home/kak-sobrat-kubik-rubika.htm