Как сделать тетраэдр из бумаги
Как сделать тетраэдр из бумаги
Как сделать тетраэдр из бумаги: развертка для склеивания
В школе на уроке геометрии многим школьникам задают сделать тетраэдр. Иногда такое задание может вызвать недоумение. Однако, такая объемная фигура делается очень просто из бумаги, если есть пошаговая инструкция по ее изготовлению. Полезные советы по практике помогут сделать его быстро и правильно.
Что такое тетраэдр
С помощью наглядной объемной фигуры детям проще научиться иметь представление о пространственном мышлении. В этом помогут объемные геометрические фигуры, сделанные своими руками из бумаги. Тетраэдр представляет собой многоугольную фигуру, которая считается простейшей. Он состоит из 4-х граней, каждая из них является равносторонним треугольником. Стороны треугольников соединяются между собой только одной гранью. В фигуре есть также четыре вершины и шесть ребер.
Людей с давних пор привлекали многогранники как удивительные символы симметрии. Они считали их божественными фигурами. Эти фигуры очень важны в развитии математического мышления детей дошкольного и школьного возраста. Они способствуют развитию геометрического представления и пространственного мышления.
На самом деле такая фигура встречается нам повсюду. Однако, сразу ее заметить сложно. Выполненная из стержней, она встречается как основа для пространственных конструкций:
Для того чтобы получить такую фигуру, можно не прибегать к сложным математическим вычислениям. Полученная модель позволит иметь наглядное представление о свойствах геометрической фигуры в объемном изображении.
Варианты выполнения
Есть несколько способов выполнения фигуры, но лучше всего использовать самый простой и распространенный. В этом случае используется готовый шаблон, либо нужно нарисовать равносторонний треугольник. У фигуры на рисунке должны быть «лепестки», чтобы склеить их потом между собой.
При использовании собственного рисунка для склеивания есть свои преимущества. Для такой фигуры обычно берут бумагу разных цветов, что дает готовому изделию наглядный и интересный вид.
Во втором варианте применяют в склеивании не отдельные треугольники, а соединенные между собой. Такую заготовку называют разверткой тетраэдра. Лепестки находятся на всех открытых гранях треугольника либо на нескольких, для нормальной фиксации.
Более сложный способ — использование модульного варианта оригами. Для этого необходимо иметь достаточное количество бумаги, а главное — терпение и усидчивость. Поскольку такая работа кропотливая, она требует времени.
В любом из приведенных вариантов потребуется терпение и желание. В каждом из них есть свои преимущества. Выбор зависит от предназначения модели.
Необходимые материалы и инструменты
Для выполнения самого простого бумажного тетраэдра понадобятся следующие предметы:
Очень важно перед началом выполнения работы ознакомиться с инструкцией. Это позволит получить одинаковые и идентичные стороны треугольника.
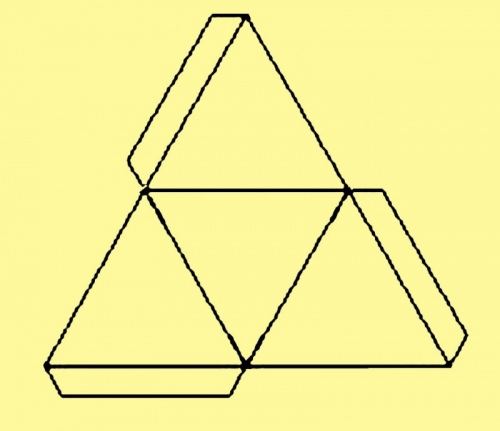
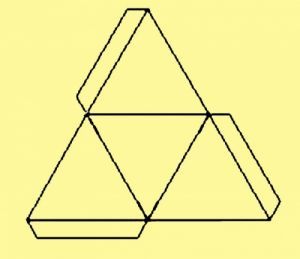
Развертка тетраэдра для склеивания
Ход работы будет зависеть от используемой бумаги. Если это картон, тогда необходимо для начала нарисовать развертку на бумаге. При использовании обычной бумаги развертка чертится прямо там.
После этого на каждой стороне полученного треугольника необходимо отложить такие же линии. Со всех концов откладываются 60 о и снова соединяются прямой линией. В итоге при правильном выполнении получается схема их 4-х равносторонних треугольников.
Для получения хорошей и удобной для склеивания развертки необходимо сделать припуски по 1 см с 3-х сторон каждого треугольника. Если все выполнено правильно, получается чертеж, как на фото.
Теперь остается аккуратно вырезать развертку, согнуть все линии, а припуски загнуть внутрь. При необходимости можно обрезать уголки. Теперь их нужно промазать клеем, стыкуя линию сгиба между стороной и припуском к стороне свободного треугольника. Припуски прижимаются к внутренним сторонам граней.
Несколько советов
При использовании плотной бумаги, например, картона в местах сгибов желательно провести линии твердым предметом. Лучше всего для этого подойдет линейка: ее ребром проводят линии.
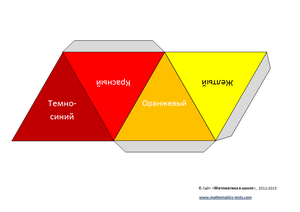
Чтобы получить разноцветный тетраэдр лучше применять цветную бумагу или же раскрасить его грани в разные цвета.
Для изготовления тетраэдра также можно применить самоклеющуюся бумагу. В таком варианте клей не понадобится.
Видео
Посмотрите, как легко и быстро можно сделать тетраэдр из бумаги.
Тетраэдр
Тетраэдр имеет следующие характеристики:
Правильный тетраэдр составлен из четырех равносторонних треугольников. Каждая его вершина является вершиной трех треугольников. Следовательно, сумма плоских углов при каждой вершине равна 180°.
Тетраэдр не имеет центра симметрии, но имеет 3 оси симметрии и 6 плоскостей симметрии.
Является ли тетраэдр пирамидой? Да, тетраэдр это треугольная пирамида у которой все стороны равны.
Может ли пирамида быть тетраэдром? Только если это пирамида с треугольным основанием и каждая из её сторон равносторонний треугольник.
Отметим, что очень редко, но встречаются геометрические тела, составленные не из правильных треугольников, и их тоже называют тетраэдры, так как они имеют четыре грани.
Математические характеристики тетраэдра
Тетраэдр может быть помещен в сферу (вписан), так, что каждая из его вершин будет касаться внутренней стенки сферы.
Радиус описанной сферы тетраэдра определяется по формуле:
Сфера может быть вписана внутрь тетраэдра.
Радиус вписанной сферы тетраэдра определяется по формуле:
Площадь поверхности тетраэдра
Для наглядности, площадь поверхности тетраэдра можно представить в виде площади развёртки. Площадь поверхности можно определить как площадь одной из сторон тетраэдра (это площадь правильного треугольника) умноженной на 4. Либо воспользоваться формулой:
Объем тетраэдра определяется по следующей формуле:
Высота тетраэдра определяется по следующей формуле:
Расстояние до центра основания тетраэдра определяется по формуле:
Вариант развертки
Древнегреческий философ Платон ассоциировал тетраэдр с «земным» элементом огонь, поэтому для построения модели этого правильного многогранника мы выбрали красный цвет.
Заметим, что это не единственный вариант развертки.
Видео. Тетраэдр из набора «Волшебные грани»
Вы можете изготовить модель тетраэдра воспользовавшись деталями для сборки из набора «Волшебные грани».
Сборка многогранника из набора:
Подробная сборка от Алексея Жигулева (youtube-канал PRO)
Подробная сборка от Алексея Жигулева (youtube-канал PRO)
вращение готового многогранника:
Видео. Вращение всех правильных многогранников
Тетраэдр из картона. Схема, как сделать поэтапно, шаблон
Тетраэдр, сделанный из бумаги или картона можно использовать в качестве модели, объясняя школьнику особенности этой фигуры в геометрии. Ещё самодельные объёмные фигуры можно использовать для декора комнаты или рабочего стола. Чтобы научиться делать тетраэдр своими руками, нужно прочесть несколько поэтапных инструкций по изготовления фигур из разных материалов.
Особенности фигуры, сколько граней и углов у тетраэдра
Тетраэдр – это объёмная геометрическая фигура треугольной формы. Она выглядит как пирамида. У тетраэдра 6 ребер, 4 вершины и 4 грани. Размеры и формы граней зависят от вида геометрической фигуры.
Какими бывают тетраэдры:
| Равногранный | Грани равны между собой. |
| Ортоцентрический | Высоты, опущенные из вершин на противоположные грани, пересекаются в одной точке. |
| Прямоугольный | Ребра, прилежащие к 1 из вершин, перпендикулярны между собой. |
| Инцентрический | Отрезки фигуры соединяют вершины с центральными точками окружностей, вписанных в противоположные грани и пересекающихся в 1 точке. |
Самый простой вид фигуры называется «правильный тетраэдр». Его грани – это односторонние треугольники. Собрать правильный тетраэдр из бумаги или картона намного проще, чем другие виды этой фигуры. Далее в статье можно рассмотреть примеры построения развёрток, а также прочесть инструкцию по склеиванию объёмной фигуры.
Что понадобиться, чтобы сделать тетраэдр своими руками
Перечень материалов и инструментов, необходимых для создания бумажного, либо картонного тетраэдра:
Желательно, чтобы бумага, на которой будет построен чертеж, была плотной. Подойдут листы для черчения, акварельная бумага или листы из альбома. Можно использовать бумагу для принтера, плотностью не менее 80 г/кв. м. Более тонкий материал будет плохо держать форму, а также рваться и мяться в процессе склеивания фигуры.
Как сделать из бумаги А4
Изготовление тетраэдра проходит в 5 этапов:
Для склеивания бумажных конструкций можно использовать обыкновенный канцелярский клей или ПВА. Для фигур, сделанных из более плотных материалов, желательно использовать клей «Момент» или качественный двухсторонний скотч без мягкой прослойки между клеевыми лентами.
Расчет размера
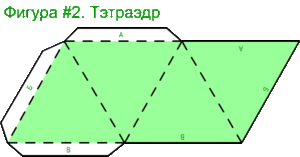
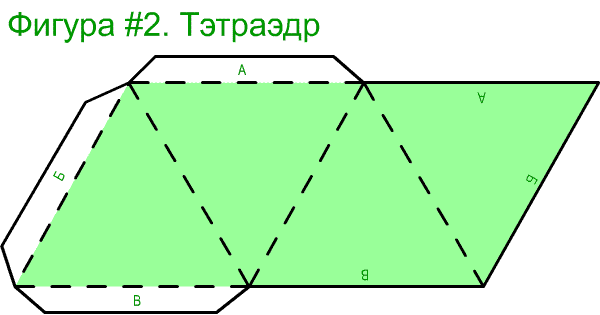
Размер будущей фигуры зависит вида развертки. Грани можно расположить по кругу. В таком случае фигура получиться небольшой. Высота такого тетраэдра будет около 6 см. Если начертить горизонтальную развёртку, где грани будут расположены в таком порядке, что образуют фигуру в виде параллелограмма. В таком случае, можно получить более крупную фигуру.
Оптимальная длина ребра тетраэдра, начерченного в горизонтальной развертке на листе формата А4 – 10 см.
В итоге получится параллелограмм с диагональю равной 26,6 см. Размер листа формата А4 равен 21×29,7 см. Диагональ листа равна 36,4 см. Поэтому развертка с диагональю 26,6 см идеально поместиться на бумаге А4, и еще останется свободнее место, чтобы начертить полосы для склеивания фигуры.
Подготовка шаблона из картона
Из картона можно сделать шаблон 1 грани тетраэдра, чтобы потом было проще построить развертку.
Как сделать заготовку поэтапно:
Ножницами аккуратно вырезать шаблон.
Построение развертки, чертежи
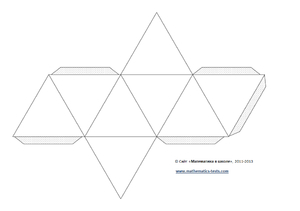
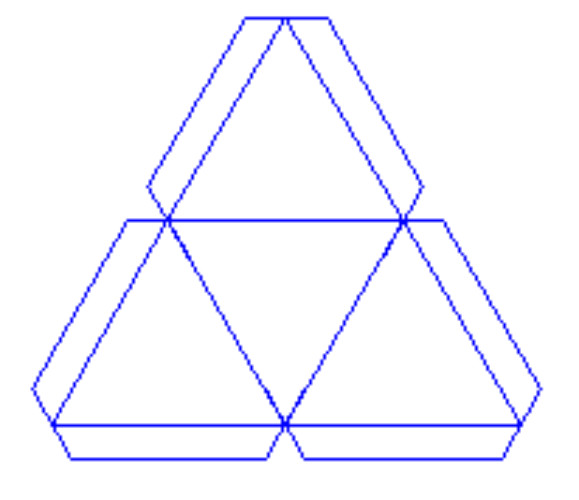
Как начертить круговую развертку тетраэдра с помощью картонного шаблона:
Ластиком удалить лишние линии.

Как начертить горизонтальную развертку тетраэдра, не используя картонный шаблон:
Работа с готовой формой, склеивание
Склеить фигуру по вырезанной развертке несложно.
Порядок действий:
Располагать «ушки» для крепления нужно изнутри. Чтобы детали хорошо склеились, необходимо придерживать пальцами места соединений в течение 10-15 сек.
Большой тетраэдр из картона
Тетраэдр из картона (сделать поэтапно можно по инструкции, представленной далее в статье) получится крепким и будет хорошо держать форму. Размер объёмной фигуры зависит от вида картона.
Какой картон можно использовать для работы:
Не цветной картон после сборки тетраэдра можно покрасить или обклеить бумагой с узорами. Если на грани небольшой фигуры наклеить календарные листы или фотографии, можно получить необычное украшение для рабочего стола.
Особенности работы с жестким картоном
Тетраэдр из картона (сделать поэтапно развертку можно, не используя шаблоны) изготавливают следуя этим правилам:
Удобнее всего работать с двухслойным гофрированным картоном. Его можно вырезать из большой коробки, в которой перевозят бытовую технику. С картоном, сложенным в 3 и более слоя, работать будет намного сложнее. Такой материал плохо гнется и тяжело склеивается.
Подготовка и вырезание шаблона
Тетраэдр из картона (сделать поэтапно можно за 1 ч) можно изготовить, используя любой вид развертки. В этом мастер-классе описан процесс составления круговой развертки, без использования шаблона.
Порядок действий:
В итоге должна получиться развертка из 4 треугольных граней. Остается добавить «ушки» для крепления. Чем шире будут «ушки», тем надежнее будет соединение. Минимальная ширина этих полосок – 5 см.
Где должны располагаться «ушки»:
Вырезать развертку канцелярским ножом.
Соединение граней
Как соединить грани фигуры:
Дождаться полного высыхания клея. Если остались излишки (застывшие капли или паутинки), их можно аккуратно срезать канцлерским ножом.
Научиться делать тетраэдр из бумаги или картона помогут инструкции, где все действия расписаны поэтапно. Главное, составить точный чертеж, а затем аккуратно вырезать развертку, используя подходящие инструменты.
Видео о создании тетраэдра из картона
Как сделать треугольную пирамиду:
Специалист в области дизайна одежды, моды, стиля, красоты и женской моды, создания одежды и аксессуаров своими руками.
Как сделать тетраэдр из бумаги своими руками поэтапно
Если вы не знаете, что такое тетраэдр, то скорее всего вы не любите геометрию. Ведь это же фигура, имеющая одинаковые стороны. Ее еще называют правильным многогранником или треугольником. У нее всего четыре стороны, но они все одинаковы! Такой же принцип заложен и у пирамид. Чтобы все стороны получились одинаковыми и идентичными – следует внимательно выполнять каждый этап.
Необходимые материалы:
Поэтапный фото урок:
Сгибаем квадратный лист бумаги пополам, подгибая нижнюю часть вверх.
Открываем. Сгибаем нижний правый уголок к полученной линии.
Раскрываем. Получаем сгиб.
Теперь можно согнуть нижний левый уголок к горизонтальной линии.
Сгибаем нижнюю часть немного вверх, чтобы сгибы сошлись.
Сгибаем нижнюю часть так, чтобы нижний сгиб размещался прямо на верхней линии квадрата.
Получаем еще одну вспомогательную горизонтальную линию.
Сгибаем правый верхний уголок к горизонтальной линии.
Далее сгибаем верхний левый уголок к этой же линии.
Проходимся по сгибам и открываем.
Начинаем складывать нашу фигуру. Берем за левый боковой треугольник и сгибаем на еще один треугольник.
Так сделаем и с правой стороны.
Теперь оставшиеся три треугольника сыграют большую роль в формировании тетраэдра. Левый и правый станут боковыми, в верхний – будет задним. Поэтому берем одновременно пальцами за боковые треугольники и тянем их вверх.
Прикладываем к левому боку тетраэдра нижнюю часть левой стороны, которую закрепим при помощи клея в середине фигуры.
Теперь складываем фигуру с правой стороны и подклеиваем выступающую часть фигуры.
Вот такая получилась объемная фигура в виде тетраэдра в технике оригами. Она непременно дополнит вашу коллекцию фигурок оригами.
Видео урок
Тетраэдр из бумаги или картона своими руками
Из истории
Тетраэдр еще одна удивительная фигура, которая довольно часто встречается в нашей жизни, но обычно наши знания о нем ограничиваются определением, свойствами и формулами из школьного курса геометрии.
Слово «тетраэдр» образовано из двух греческих слов: tetra – переводиться как четыре и hedra – означает основание, грань; в каждой вершине тетраэдра сходятся по 3 грани. Эта фигура имеет 4 грани, 6 ребер и 4 вершины.
С самых древних времен представления людей о красоте были связаны с симметрией. Возможно, этим объясняется интерес людей к многогранникам – удивительным символам симметрии, привлекавшим внимание выдающихся мыслителей и людей всех эпох. Уже во времена Пифагора дивились их красоте и симметрии.
Ученики Пифагора считали, что правильные многогранники – это божественные фигуры и использовали их в философских сочинениях. Первоосновам бытия – огню, воздуху, воде, земле придавалась форма соответственно октаэдра, икосаэдра, тетраэдра, куба, а Вселенная представлялась в форме додекаэдра.
Ученики Платона продолжили изучение перечисленных тел, поэтому эти многогранники называют Платоновыми телами.
Роль задач о тетраэдрах очень высока в развитии математического мышления школьников. Эти задачи стимулируют накопление геометрических представлений и знаний, способствуют развитию пространственного мышления, что особенно важно в процессе изучения стереометрии.
Где можно встретить тетраэдр? Тетраэдр, такая удивительная геометрическая фигура, которая встречается нам повсюду, но с первого взгляда ее не так просто заметить. Тетраэдр может образовать жёсткую конструкцию.
Выполненный из стержней, его часто используют в качестве основы для пространственных конструкций балок, ферм мостов, пролётов зданий, перекрытий и т. д. Прямоугольный тетраэдр давно используется в оптике. На велосипедах отражатели катафоты имеют форму тетраэдра.
Благодаря свойствам тетраэдра, катафоты отражают свет и другим людям и водителям видно велосипедиста. Если внимательно присмотреться, то внутри катафота видно множество форм тетраэдра.
Виды тетраэдра
Тетраэдр – подсказанное нам природой идеальное равновесие, в основе которого, идеальность равнобедренного треугольника. Тетраэдр – треугольник, но только в объемном виде, в наше время его можно назвать 3D треугольник.
Пополнить свою коллекцию геометрических фигур новой фигурой – тетраэдром, вы можете используя развертки, представленные на нашем сайте. Тетраэдр, собранный по этим разверткам можно использовать для обучения, например, что бы научить детишек считать, узнавать цвета, можно объяснить, что такое плоскость и объем, что такое треугольник др.
Развертка тетраэдра из бумаги или из картона
| Схема тетраэдра с арабскими цифрами 1,2,3,4 (грань 10 см) | Схема тетраэдра с арабскими цифрами 5,6,7,8 (грань 10 см) | Схема тетраэдра с арабскими цифрами 0,1,2,9 (грань 10 см) |
 |  |  |
| JPG | JPG | JPG |
| Схема разноцветного тетраэдра №1 (грань 10 см) | Схема разноцветного тетраэдра №2 (грань 10 см) | Схема разноцветного тетраэдра №3 (грань 10 см) |
 |  |  |
| JPG | JPG | JPG |
| Схема простого тетраэдра (грань — 10 см) | Схема тетраэдра с формулами (грань 10 см) | Схема тетраэдра с героями советских мультиков (грань — 10 см) |
 |  | |
| JPG | JPG | JPG |
| Тетраэдр-календарь на 2013 год (январь-апрель, грань 10 см) | Тетраэдр-календарь на 2013 год (май-август, грань 10 см) | Тетраэдр-календарь на 2013 год (сентябрь-декабрь, грань 10 см) |
 |  | |
| JPG | JPG | JPG |
Как из бумаги сделать тетраэдр?
Тетраэдр – самая простая фигура из многоугольников. Он состоит из четырех граней, каждая из которых представляет собой равносторонний треугольник, при этом каждая из сторон соединяется с другой всего лишь одной гранью. При изучении свойств этой трехмерной геометрической фигуры для наглядности лучше всего сделать модель тетраэдра из бумаги.
Как склеить тетраэдр из бумаги?
Для построения простого тетраэдра из бумаги нам понадобится:
Несколько дополнительных рекомендаций:
Как из бумаги сделать тетраэдр без склеивания?
Предлагаем вашему вниманию мастер-класс, в котором рассказывается, как собрать 6 тетраэдров из бумаги в единый модуль при помощи техники оригами.
Если вы справились с тетраэдром, можно продолжить и смастерить из бумаги призму, икосаэдр, параллелепипед и другие геометрические фигуры.
В помощь юным умельцам: как из бумаги сделать тетраэдр
Для работы не понадобится вдаваться в сложные математические вычисления, не придется рассчитывать ни обьем тетраэдра, ни его площадь, ни высоту. Единственное, что потребуется, — это лист бумаги, карандаш, ножницы и клей, а то и восве можно обойтись только бумагой.
Так как из бумаги сделать тетраэдр, имея все необходимые материалы? Существует несколько способов. Первый и самый распространенный вариант: вырезать четыре отдельных треугольника с так называемыми «лепестками», которые затем склеиваются между собой.
Вы можете нарисовать равносторонний треугольник самостоятельно или же воспользоваться готовым шаблоном. К преимуществам этого способа можно отнести 
Второй способ заключатся в склеивании не отдельных треугольников, а уже соединенных между собой (так называемая развертка тетраэдра). В этом случае тоже может быть несколько вариантов, а именно: лепестки для склейки могут находиться на всех открытых гранях или же только на некоторых, тех, которые представляют минимум для надежной фиксации.
И, наконец, рассматривая третий способ того, как из бумаги сделать тетраэдр, мы увидим, что нет нужды даже в каких-либо клеящих веществах, ведь 
Каждый из перечисленных выше вариантов имеет свои преимущества перед остальными, и все они являются достойными и эффективными. И выбирать способ, который подходит именно вам, следует, опираясь на наличие времени и терпения, а также предназначение будущей модели тетраэдра.
Как сделать тетраэдр из бумаги: развертка для склеивания
В школе на уроке геометрии многим школьникам задают сделать тетраэдр. Иногда такое задание может вызвать недоумение. Однако, такая объемная фигура делается очень просто из бумаги, если есть пошаговая инструкция по ее изготовлению. Полезные советы по практике помогут сделать его быстро и правильно.
Что такое тетраэдр
С помощью наглядной объемной фигуры детям проще научиться иметь представление о пространственном мышлении. В этом помогут объемные геометрические фигуры, сделанные своими руками из бумаги.
Тетраэдр представляет собой многоугольную фигуру, которая считается простейшей. Он состоит из 4-х граней, каждая из них является равносторонним треугольником. Стороны треугольников соединяются между собой только одной гранью.
В фигуре есть также четыре вершины и шесть ребер.
Людей с давних пор привлекали многогранники как удивительные символы симметрии. Они считали их божественными фигурами. Эти фигуры очень важны в развитии математического мышления детей дошкольного и школьного возраста. Они способствуют развитию геометрического представления и пространственного мышления.
На самом деле такая фигура встречается нам повсюду. Однако, сразу ее заметить сложно. Выполненная из стержней, она встречается как основа для пространственных конструкций:
Для того чтобы получить такую фигуру, можно не прибегать к сложным математическим вычислениям. Полученная модель позволит иметь наглядное представление о свойствах геометрической фигуры в объемном изображении.
Варианты выполнения
Есть несколько способов выполнения фигуры, но лучше всего использовать самый простой и распространенный. В этом случае используется готовый шаблон, либо нужно нарисовать равносторонний треугольник. У фигуры на рисунке должны быть «лепестки», чтобы склеить их потом между собой.
При использовании собственного рисунка для склеивания есть свои преимущества. Для такой фигуры обычно берут бумагу разных цветов, что дает готовому изделию наглядный и интересный вид.
Во втором варианте применяют в склеивании не отдельные треугольники, а соединенные между собой. Такую заготовку называют разверткой тетраэдра. Лепестки находятся на всех открытых гранях треугольника либо на нескольких, для нормальной фиксации.
Более сложный способ — использование модульного варианта оригами. Для этого необходимо иметь достаточное количество бумаги, а главное — терпение и усидчивость. Поскольку такая работа кропотливая, она требует времени.
В любом из приведенных вариантов потребуется терпение и желание. В каждом из них есть свои преимущества. Выбор зависит от предназначения модели.
Необходимые материалы и инструменты
Для выполнения самого простого бумажного тетраэдра понадобятся следующие предметы:
Очень важно перед началом выполнения работы ознакомиться с инструкцией. Это позволит получить одинаковые и идентичные стороны треугольника.
Развертка тетраэдра для склеивания
Ход работы будет зависеть от используемой бумаги. Если это картон, тогда необходимо для начала нарисовать развертку на бумаге. При использовании обычной бумаги развертка чертится прямо там.
Для начала нужно начертить прямую линию, которая является гранью фигуры. С двух сторон необходимо отметить углы по 60о. После этого полученные точки соединяются прямой линией до их пересечения. В итоге получается равносторонний треугольник.
После этого на каждой стороне полученного треугольника необходимо отложить такие же линии. Со всех концов откладываются 60о и снова соединяются прямой линией. В итоге при правильном выполнении получается схема их 4-х равносторонних треугольников.
Для получения хорошей и удобной для склеивания развертки необходимо сделать припуски по 1 см с 3-х сторон каждого треугольника. Если все выполнено правильно, получается чертеж, как на фото.
Теперь остается аккуратно вырезать развертку, согнуть все линии, а припуски загнуть внутрь. При необходимости можно обрезать уголки. Теперь их нужно промазать клеем, стыкуя линию сгиба между стороной и припуском к стороне свободного треугольника. Припуски прижимаются к внутренним сторонам граней.
Несколько советов
При использовании плотной бумаги, например, картона в местах сгибов желательно провести линии твердым предметом. Лучше всего для этого подойдет линейка: ее ребром проводят линии.
Чтобы получить разноцветный тетраэдр лучше применять цветную бумагу или же раскрасить его грани в разные цвета.
Для изготовления тетраэдра также можно применить самоклеющуюся бумагу. В таком варианте клей не понадобится.
Видео
Посмотрите, как легко и быстро можно сделать тетраэдр из бумаги.
Как собирать паперкрафт развертки: пособие для чайников
Поделки из фигур доступны для занятий с детьми с самого младшего возраста.
Для того, чтобы заинтересовать ребенка изготовлением поделки из геометрических фигур, можно предложить ему интерактивную игру на основе сказки “Мышонок и карандаш”. Затею эту можно осуществить в домашних условиях на занятиях в детском саду. Необходимо заранее приготовить элементы, из которых состоит кошка: круги, овалы и треугольники.
Увлекательная игра поможет сделать творческий процесс интереснее для очень активных детей.
Дед мороз и Снегурочка рисунок карандашом на Новый год 2021
Плоские геометрические фигуры из бумаги – Строим замок
В этом упражнении вы можете скачать плоские геометрические фигуры из бумаги и построить из них замок, то есть выложить их на столе таким образом, чтобы получился заданный силуэт замка.
Для начала скачайте во вложениях бланки с заданием и распечатайте на принтере. Затем вырежьте геометрические фигуры (квадрат, трапеция, полукруг и треугольник), которые даны к этому заданию.
Все карточки с заданиями даны с увеличением уровня сложности (от 1 до 6 задания).
Все карточки с замками можно распечатывать на обычной офисной белой бумаге. А геометрические фигуры нужно распечатать на цветном картоне. Если нет цветного картона, можно использовать для распечатки цветную бумагу, а затем наклеить бумагу на лист картона и вырезать фигуры.
После этого подробно объесните ребенку инструкцию к выполнению упражнения.
“Строители, прежде чем строить какое-либо здание, смотрят сначала на его чертеж или схему, в которых показано каким оно должно быть. Такие чертежи бывают разными.
Вот например, один из них”, – взрослый показывает одну или две игровых схемы замка с нашего задания. – “Тебе нужно мысленно представить из каких частей состоит каждый замок, руководствуясь теми фигурами, которые можно использовать для строительства.
” – взрослый показывает все геометрические фигуры, которые заранее вырезаны из цветного картона.
Очень важно начинать занятие, не используя подсказки, то есть нужно закрывать от ребенка геометрические фигуры, которые нарисованы рядом с силуэтом каждого замка. Пусть ребенок сам подумает, какие фигуры и какого размера ему понадобятся для строительства данного замка. И только если он испытвает трудности, можно приоткрыть для него подсказку.
Также не нужно допускать, чтобы ребенок накладывал вырезанные геометрические фигуры из бумаги на силуэт замка, так как при этом он не будет развивать наглядно-образное мышление. Старайтесь, чтобы всю основную работу ребенок проводил в уме, а не методом подбора.
Что нужно для моделирования геометрических фигур?
Подготовьте рабочий стол и материалы. Как известно, обычно в детский садик просят сделать самые разные подделки, да и первые школьные классы тоже любят занять детей творчеством.
Творчество из геометрических фигур развивает пространственное мышление, логику, понятие цвета, формы и применения объекта.
Таким образом, круг может превратиться в основу для солнца или озера, а например несколько треугольников могут сделать забавную белочку, которая будет гулять на зеленом лугу.Суть геометрического творчества такова, что в нем нет ограничений по использованию форм. Это могут быть фигуры как строгой пропорции, так и нарезка каких-то деталей.
Еще один популярный вид моделирования фигурами – рваная геометрия.Для «рваной» геометрии вам просто нужно нарвать фигурки разного размера. Отлично подойдет вариант нарванных полосок, которые потом превратятся в маленькие кубики.
Поделки из геометрических фигур для детей приобрели большую популярность за счет того, что детям очень нравится играть с разнообразием подачи формы и цвета.
Схема как сделать треугольник из бумаги. Пирамида из бумаги своими руками. Схемы и способы изготовления
Как сделать объемные геометрические фигуры
Дети познают мир в процессе игры и творчества. Трехмерные фигуры, выполненные своими руками, помогут познакомиться с удивительной наукой — геометрией.
Примеры трафаретов и шаблонов можно скачать из Интернета и распечатать. Затем все фигуры вырезают и склеивают. Дети старшего возраста могут самостоятельно нарисовать развертку нужной фигуры, малышам помогают родители,.
Геометрические объекты делают из бумаги (белой или цветной), картона. Из последнего материала они получаются плотными и прочными.
Все об уходе за садовыми луковичными многолетниками
Как сделать тетраэдр
Дабы сделать тетраэдр, необходимо взять лист бумаги, ножницы и клей. После этого следует вырезать из бумаги развертку тетраэдра и склеить. Если найдется 4 листа разноцветной бумаги, то тетраэдр получится ещё прекраснее.
Вам понадобится
Инструкция
1. Дабы сделать тетраэдр, нужно взять лист плотной бумаги либо картона и нарисовать на нем изображенную на чертеже развертку. Размер развертки может быть произвольным. Необязательно копировать представленную на рисунке фигуру. Реально, развертка состоит из четырех равносторонних, равных между собой, треугольников (не считая предуготовленных для склеивания лепестков).
2. После этого надобно ножницами старательно вырезать нарисованную на бумаге развертку и согнуть ее по каждому линиям. Дабы места сгибов получились ровными и отчетливыми дозволено воспользоваться каким-либо металлическим предметом. Скажем, ручками ножниц. Если заготовка вырезается из картона либо толстой, довольно плотной бумаги, то линии сгибов нужно надрезать чем-то дюже острым, скажем лезвием бритвы.
3. Позже этого «выкройку» нужно склеить. Лепестки для склеивания граней необходимо разместить вовнутрь образовавшейся фигуры. Если на картоне производились надрезы, то они обязаны оказаться снаружи тетраэдра.
Совет 2: Как склеить тетраэдр
Изготовить модель тетраэдра дозволено из самых различных материалов. Один из особенно доступных вариантов — склеить его из бумаги. При этом клей требуется не неизменно, от того что самоклеющаяся бумага тоже подходит для таких целей.
Вам понадобится
Инструкция
1. Начните с построения развертки. Если вы собираетесь клеить тетраэдр из обыкновенной плотной бумаги, развертку дозволено сделать прямо на ней. Для самоклеющейся бумаги отличнее начертите выкройку, как это выполняется в классическом моделировании. Дозволено применять и компьютер с AutoCAD либо любым иным графическим редактором, дозволяющим строить положительные многоугольники.
2. Постройте равносторонний треугольник. Если вы делаете это на бумаге, то начертите отрезок, равный ребру тетраэдра. С подмогой транспортира отложите от его концов углы, равные 60°. Проведите через полученные точки прямые до их пересечения.
3. На всякой стороне теснее имеющегося треугольника постройте верно такие же. Всякая сторона начального треугольника будет являться и стороной иного. Верно так же отложите от концов отрезка углы по 60°, но по направлению от теснее нарисованной фигуры. Через полученные точки проведите прямые до их пересечения. У вас должна получиться конструкция из четырех идентичных равносторонних треугольников.
4. Для того, дабы полученную развертку дозволено было склеить, у 3 треугольников сделайте припуски. К одной из сторон прибавьте 1 см по каждой ее длине. Поверните фигуру по часовой стрелке и сделайте такой же припуск для иной грани, а после этого и для третьей. Вырежьте развертку. Если надобно, обведите ее на иную бумагу.
5. Согните развертку по каждому линиям так, дабы у вас получилась пирамидка. Припуски загните вовнутрь. Если необходимо, срежьте углы. Намажьте припуски клеем и прижмите их к внутренним сторонам соседних граней, совместив линию между треугольником и припуском со свободной стороной соседнего треугольника. Если тетраэдр из самоклеющейся бумаги, линии класснее процарапать, после этого согнуть фигуру и прижать припуск к грани.
Полезный совет
По тому же тезису дозволено склеить модели и других геометрических тел. Для построения разверток значимо знать угол наклона боковых граней к нижней. У тетраэдра все грани равны, следственно безусловно все равно, какая из них будет считаться дном. Для построения других типов пирамид начертите вначале дно, а после этого — рассчитайте и постройте боковые грани.
Видео по теме
Обратите внимание!
Тетраэдр является примитивной фигурой среди всех многогранников. Он состоит каждого из четырех граней — равносторонних треугольников. Четыре грани – это наименьшее число граней, отделяющих замкнутую часть пространства. Тетраэдр владеет многими свойствами верных многогранников. Все его грани – положительные (равносторонние) многоугольники (треугольники), причём всякая из них отделяется ребром ровно от одной грани. Все углы тетраэдра равны между собой.
Полезный совет
Дабы тетраэдр стал разноцветным, дозволено покрасить всякую грань фигуры в обособленный цвет. Цветной тетраэдр дозволено также получить, применяя развертку, вырезанную из различных листов цветной бумаги. При этом необходимо подготовить четыре простейших развертки – всякая в виде равностороннего треугольника. Склейка разноцветного тетраэдра производится подобно примитивный (одноцветной) фигуре.
Как склеить тетраэдр: описываем суть
Дабы сделать тетраэдр, необходимо взять лист бумаги, ножницы и клей. После этого следует вырезать из бумаги развертку тетраэдра и склеить. Если найдется 4 листа разноцветной бумаги, то тетраэдр получится ещё прекраснее.
Вам понадобится
Что такое тетраэдр
С помощью наглядной объемной фигуры детям проще научиться иметь представление о пространственном мышлении. В этом помогут объемные геометрические фигуры, сделанные своими руками из бумаги. Тетраэдр представляет собой многоугольную фигуру, которая считается простейшей. Он состоит из 4-х граней, каждая из них является равносторонним треугольником. Стороны треугольников соединяются между собой только одной гранью. В фигуре есть также четыре вершины и шесть ребер.
Людей с давних пор привлекали многогранники как удивительные символы симметрии. Они считали их божественными фигурами. Эти фигуры очень важны в развитии математического мышления детей дошкольного и школьного возраста. Они способствуют развитию геометрического представления и пространственного мышления.
На самом деле такая фигура встречается нам повсюду. Однако, сразу ее заметить сложно. Выполненная из стержней, она встречается как основа для пространственных конструкций:
Для того чтобы получить такую фигуру, можно не прибегать к сложным математическим вычислениям. Полученная модель позволит иметь наглядное представление о свойствах геометрической фигуры в объемном изображении.
Как склеить тетраэдр из бумаги?
Для построения простого тетраэдра из бумаги нам понадобится:
Несколько дополнительных рекомендаций:
Инструкция
1. Начните с построения развертки. Если вы собираетесь клеить тетраэдр из обыкновенной плотной бумаги, развертку дозволено сделать прямо на ней. Для самоклеющейся бумаги отличнее начертите выкройку, как это выполняется в классическом моделировании. Дозволено применять и компьютер с AutoCAD либо любым иным графическим редактором, дозволяющим строить положительные многоугольники.
2. Постройте равносторонний треугольник. Если вы делаете это на бумаге, то начертите отрезок, равный ребру тетраэдра. С подмогой транспортира отложите от его концов углы, равные 60°. Проведите через полученные точки прямые до их пересечения.
3. На всякой стороне теснее имеющегося треугольника постройте верно такие же. Всякая сторона начального треугольника будет являться и стороной иного. Верно так же отложите от концов отрезка углы по 60°, но по направлению от теснее нарисованной фигуры. Через полученные точки проведите прямые до их пересечения. У вас должна получиться конструкция из четырех идентичных равносторонних треугольников.
4. Для того, дабы полученную развертку дозволено было склеить, у 3 треугольников сделайте припуски. К одной из сторон прибавьте 1 см по каждой ее длине. Поверните фигуру по часовой стрелке и сделайте такой же припуск для иной грани, а после этого и для третьей. Вырежьте развертку. Если надобно, обведите ее на иную бумагу.
5. Согните развертку по каждому линиям так, дабы у вас получилась пирамидка. Припуски загните вовнутрь. Если необходимо, срежьте углы. Намажьте припуски клеем и прижмите их к внутренним сторонам соседних граней, совместив линию между треугольником и припуском со свободной стороной соседнего треугольника. Если тетраэдр из самоклеющейся бумаги, линии класснее процарапать, после этого согнуть фигуру и прижать припуск к грани.
Полезный совет
По тому же тезису дозволено склеить модели и других геометрических тел. Для построения разверток значимо знать угол наклона боковых граней к нижней. У тетраэдра все грани равны, следственно безусловно все равно, какая из них будет считаться дном. Для построения других типов пирамид начертите вначале дно, а после этого — рассчитайте и постройте боковые грани.
Видео по теме
Обратите внимание!
Тетраэдр является примитивной фигурой среди всех многогранников. Он состоит каждого из четырех граней — равносторонних треугольников. Четыре грани – это наименьшее число граней, отделяющих замкнутую часть пространства. Тетраэдр владеет многими свойствами верных многогранников. Все его грани – положительные (равносторонние) многоугольники (треугольники), причём всякая из них отделяется ребром ровно от одной грани. Все углы тетраэдра равны между собой.
Полезный совет
Дабы тетраэдр стал разноцветным, дозволено покрасить всякую грань фигуры в обособленный цвет. Цветной тетраэдр дозволено также получить, применяя развертку, вырезанную из различных листов цветной бумаги. При этом необходимо подготовить четыре простейших развертки – всякая в виде равностороннего треугольника. Склейка разноцветного тетраэдра производится подобно примитивный (одноцветной) фигуре.
Как из бумаги сделать тетраэдр без склеивания?
Предлагаем вашему вниманию мастер-класс, в котором рассказывается, как собрать 6 тетраэдров из бумаги в единый модуль при помощи техники оригами.
Если вы справились с тетраэдром, можно продолжить и смастерить из бумаги призму, икосаэдр, параллелепипед и другие геометрические фигуры.
Виды тетраэдра
Фигуру тетраэдр можно разделить на несколько видов, какие они бывают?
Равногранный тетраэдр, все его грани являются равными между собой треугольниками;
Ортоцентрический тетраэдр, высоты, опущенные из вершин на противоположные грани, пересекаются в одной точке;
Прямоугольный тетраэдр, ребра, прилежащие к одной из вершин, являются перпендикулярными между собой;
Правильный тетраэдр, это тетраэдр, грани которого являются равносторонними треугольниками,
Инцентрический тетраэдр, его отрезки соединяют вершины с центрами окружностей, которые вписаны в противоположные грани и пересекаются в одной точке.
Выделяют так же каркасный тетраэдр, соразмерный тетраэдр.
Тетраэдр – подсказанное нам природой идеальное равновесие, в основе которого, идеальность равнобедренного треугольника. Тетраэдр – треугольник, но только в объемном виде, в наше время его можно назвать 3D треугольник.
Как сделать тетраэдр из бумаги? Фото, схемы, видео?
вот так можно сделать из бумаги тетрадь.
Для того, чтобы сделать тетраэдр, нужно вырезать из бумаги заготовку по схемам, предложенным ниже, нужно склеить все выступающие части клеем и приложить к нужным краям, немного подождать и эта фигура готова. Вот схемы:
Если выбирать из многоугольников, то можно сказать, что тетраэдр довольно простая в изготовлении фигура. При должной сноровке изготовить его можно всего за пятнадцть минут свободного времени и понадобится нам для этого всего лишь полоска бумаги. Схема, представленная на видео позволяет собрать тетраэдр из полосы любого размера. При этом дополнительные канцелярские предметы вроде ножниц и клея нам не понадобится. Тетраэдр будет изготовлен из цельной полосы методом згибания. Подробнее можно посмотреть на этом видео:
Кроме колокольчиков, процесс изготовления которых показан на видео ниже, можно сделать колокольчики из гофрированной тары из-под яиц.
Сначала вырезаем отдельные ячейки, а из мест сгиба формируем будущие листья.
После окрашивания вырезанных ячеек в красный цвет, и листиков в зеленый, нанизываем на толстую нить поочередно листики и чашу цветка, а внутрь привязываем бубенчик, снятый с рыбацких бубенчиков.
Сделать Елочку из кружева очень просто.
Берете плотный картон, складываете его конусом, закрепляете степлером или клеем ПВА. Заполняете монтажной пеной.
Обклеиваем конус полосками белой бумаги при помощи клея ПВА. Получается каркас будущей елки.
Выбираем кружева. Они могут быть широкие, тонкие, присборенные. Через равные промежутки пришиваем на кружево красивые бусины и бантики. Но можно этого не делать, а наклеить все позже, в конце.
Закреплять кружево надо с основания елки, с дна.
Фиксируем кружево с помощью клеевого пистолета. Разрезаем кружево в 4 местах и приклеиваем к конусу. Таким образом кружево ляжет плотнее. Сделав круг из кружева, начинаем следующий ряд. Так же разрезаем кружево в 4 местах. Третий ряд при широком кружеве будет последний. Если же кружево узкое, можно наклеивать его наматывая по спирали.
На верхушку приклеиваем бантик, но можно и без него.
Украсить елочку можно пустив канву по спирали, она будет выполнять роль гирлянды. Можно приклеить бусины и паетки.
Немного времени и стараний и у Вас будет оригинальная, нежная елочка.
В интернете такое количество вариантов исполнения снежинок, что глаза разбегаются! Хотела предложить сразу несколько вариантов, но решила выбрать из них самый простой и в то же время красивый. Сложных вариантов не предлагаю, не люблю заморачиваться, потому что времени жалко. Этот вариант много времени не займёт. Спасибо тем, что такие видео выкладывает.
7 простых вариантов пирамиды-оригами
Существует два типа пирамид-оригами ‒ треугольные и четырёхугольные, в зависимости от фигуры, лежащей в основании. Первая разновидность также известна как тетраэдр, она часто используется для составления бумажных панно. Из четырёхугольных пирамид делают праздничный декор и оригинальные упаковочные коробочки.
Тетраэдр
Треугольные пирамидки в технике оригами можно сложить из прямоугольного листа бумаги формата А4, традиционного квадрата или модулей. Схемы сборки для каждой модели отличаются по степени сложности. Самый лёгкий и быстрый вариант ‒ это пирамидка без дна, построенная на базовой форме «Блин».
Пошаговая инструкция:
Изготовим большое количество таких модулей-тетраэдров и сложим из них оригинальную абстрактную картину:
Если нужна упаковка для подарка, можно изготовить тетраэдр из трёх модулей. Эффектно раскрываясь, он напоминает цветок, внутри которого ждёт приятный сюрприз. Для этой модели нам понадобятся 3 квадрата, размером 15х15 см.
Пошаговая инструкция:
Каждый лист сгибаем по диагонали. Намечаем середину получившегося треугольника. Располагаем его открытым концом вниз. Правый и левый угол опускаем к вершине.
Соединяем модули между собой, вставляя друг в друга.
Третий вариант изготовления пирамиды представлен в видео-инструкции:
Четырёхугольная модель
Пирамида, в основании которой лежит квадрат, была хорошо известна древним цивилизациям. В Египте, Америке, Нубии и Китае возводили культовые сооружения такой формы, которые одновременно служили усыпальницами, храмами и
обсерваториями. Учёные отмечают уникальные свойства геометрических построек, в том числе способность консервировать всё, что попадает внутрь. Так ли это на самом деле, нетрудно проверить, если сделать аналогичную пирамиду из бумаги ‒ конечно, выбрав меньший масштаб.
Пошаговая инструкция:
А это ‒ коробочка в форме пирамиды. В неё можно положить сладости на детской вечеринке или небольшой сувенир.
Дерево
Не совсем обычное применение пирамидке-оригами нашёл японский дизайнер Макото Ямагути. В декабрьском номере журнала NOA Magazine за 1975 год он опубликовал модель, которую назвал рождественским деревом. Ямагути использовал три последовательно уменьшающихся пирамиды-оригами, сложенные из квадратов 15х15 см, 12х12 см, 8х8 см. Его схема получила широкое распространение, причём модули, из которых сложено дерево, используются и отдельно ‒ в качестве украшений или бижутерии.
Для этой модели лучше брать бумагу со сторонами одного цвета, иначе изнанка будет видна в нижней части кроны, нарушая целостность изделия.
Верхушка дерева:
Верхний слой складываем и поворачиваем вправо. Продолжаем тянуть лист, пока не соединятся красные точки, а зелёная опустится вниз, образуя выступ. Модуль из плоского становится объёмным.
Ствол дерева:
Осталось собрать наше рождественское дерево. Пирамиды из бумаги сделаны таким образом, что соединяются без клея.
Теперь можно пополнить коллекцию оригами-деревьев ещё одним ярким экземпляром.
Как сделать правильный тетраэдр. Правильный тетраэдр (пирамида). Как склеить тетраэдр из бумаги
Таким образом, тетраэдр – это простейший многогранник, гранями которого являются четыре треугольника.

Высотой тетраэдра называется отрезок, который соединяет вершину с точкой, расположенной на противоположной грани и перпендикулярный к ней.
Медианой тетраэдра называется отрезок, который соединяет вершину с точкой пересечения медиан противоположной грани.
Бимедианой тетраэдра называется отрезок, который соединяет середины скрещивающихся ребер тетраэдра.
Так как тетраэдр – это пирамида с треугольным основанием, то объем любого тетраэдра можно рассчитать по формуле
Правильный тетраэдр – частный вид тетраэдра
Тетраэдр, у которого все грани равносторонние треугольник называется правильным.
Свойства правильного тетраэдра:

BM=, DM=, BD=a,
p=1/2 (BM+BD+DM)= 
Подставим эти значения в формулу высоты. Получим

Вынесем 1/2a. Получим

Применим формулу разность квадратов
После небольших преобразований получим
Объем любого тетраэдра можно рассчитать по формуле
,
где 
Подставив эти значения, получим
Таким образом формула объема для правильного тетраэдра
где a –ребро тетраэдра
Вычисление объема тетраэдра, если известны координаты его вершин
Пусть нам даны координаты вершин тетраэдра
ТЕКСТОВАЯ РАСШИФРОВКА УРОКА:
Добрый день! Мы продолжаем с вами изучать тему: «Параллельность прямых и плоскостей».
Я думаю, уже понятно, что сегодня речь пойдет о многогранниках- поверхностях геометрических тел, составленных из многоугольников.
А именно о тетраэдре.
Проводить изучение многогранников будем по плану:
1. определение тетраэдра
2. элементы тетраэдра
3. развертка тетраэдра
4. изображение на плоскости
1. построим треугольник АBC
2. точка D, не лежащая в плоскости этого треугольника
3. соединяем точку D отрезками с вершинами треугольника ABC. Получим треугольники DAB, DBC и DCA.
Определение: Поверхность составленная из четырех треугольников АBC, DAB, DBC и DCA называется тетраэдром.
Сколько граней, ребер и вершин имеет тетраэдр?
Тетраэдр имеет четыре грани, шесть ребер и четыре вершины
Два ребра тетраэдра, не имеющие общих вершин, называются противоположными.
На рисунке противоположными являются ребра AD и BC, BD и AC, CD и AB
Для изготовления тетраэдра из бумаги вам потребуется следующая развертка,
ее нужно перенести на плотную бумагу, вырезать, согнуть по пунктирным линиям и склеить.
На плоскости тетраэдр изображается
В виде выпуклого или невыпуклого четырехугольника с диагоналями. При этом штриховыми линиями изображаются невидимые ребра.
На первом рисунке AC- невидимое ребро,
Решим несколько типовых задач на тетраэдр:
Найти площадь развертки правильного тетраэдра с ребром 5 см.
Решение. Начертим развертку тетраэдра
(на экране появляется развертка тетраэдра)
Данный тетраэдр состоит из четырех равносторонних треугольников, следовательно, площадь развертки правильного тетраэдра равна площади полной поверхности тетраэдра или площади четырех правильных треугольников.
Площадь правильного треугольника ищем по формуле:
Тогда получаем площадь тетраэдра равна:
Подставим в формулу длину ребра а=5 см,
Ответ: Площадь развертки правильного тетраэдра
Постройте сечение тетраэдра плоскостью проходящей через точки M, N и K.
а) Действительно, соединим точки M и N (принадлежат грани ADC), точки M и K(принадлежат грани ADB), точки N и K (грани DBC). Сечением тетраэдра является треугольник MKN.
б) Соединим точки M и K (принадлежат грани ADB), точки K и N(принадлежат грани DCB), далее прямые MK и AB продолжить до пересечения и поставить точку P. Прямая PN и точка T лежат в одной плоскости АВС и теперь можно построить пересечение прямой МК с каждой гранью. В результате получается четырехугольник MKNT, который является искомым сечением.
Тетраэдр – самая простая фигура из многоугольников. Он состоит из четырех граней, каждая из которых представляет собой равносторонний треугольник, при этом каждая из сторон соединяется с другой всего лишь одной гранью. При изучении свойств этой трехмерной геометрической фигуры для наглядности лучше всего сделать модель тетраэдра из бумаги.
Как склеить тетраэдр из бумаги?
Для построения простого тетраэдра из бумаги нам понадобится:
Как из бумаги сделать тетраэдр без склеивания?
Предлагаем вашему вниманию мастер-класс, в котором рассказывается, как собрать 6 тетраэдров из бумаги в единый модуль при помощи техники оригами.
Если вы справились с тетраэдром, можно продолжить и смастерить
Сегодня поговорим об элементах и свойствах тетраэдра, а также узнаем формулы нахождения у этих элементов площади, объема и других параметров.
Элементы четырехгранника
Отрезок, выпущенный из любой вершины тетраэдра и опущенный на точку пересечения медиан грани, являющейся противоположной, называется медианой.
Высота многоугольника представляет собой нормальный отрезок, опущенный из вершины напротив.
Бимедианой называется отрезок, соединяющий центры скрещивающихся ребер.
Свойства тетраэдра
1) Параллельные плоскости, которые проходят через два скрещивающихся ребра, образуют описанный параллелепипед.
3) Плоскость разделяет тетраэдр на две равные по объему части, если проходит через середину двух скрещивающихся ребер.
Виды тетраэдра
Видовое разнообразие фигуры достаточно широко. Тетраэдр может быть:
Остановимся подробно на правильном тетраэдре, свойства которого практически не отличаются.
Формулы четырехгранника
Высота тетраэдра равна произведению корня из 2/3 и длины ребра.
Объем тетраэдра находится так же, как объем пирамиды: корень квадратный из 2 разделить на 12 и умножить на длину ребра в кубе.
Остальные формулы для расчета площади и радиусов окружностей представлены выше.
Свойства равногранного тетраэдра:
Ортоцентрический тетраэдр
Все высоты, опущенные из вершин на противоположные грани, пересекаются в одной точке.
Свойства ортоцентрического тетраэдра:
Прямоугольный тетраэдр
Каркасный тетраэдр
Это тетраэдр, отвечающий любому из следующих условий :
Соразмерный тетраэдр
Свойства соразмерного тетраэдра:
Инцентрический тетраэдр
У этого типа отрезки, соединяющие вершины тетраэдра с центрами окружностей, вписанных в противоположные грани, пересекаются в одной точке. Свойства инцентрического тетраэдра:
Правильный тетраэдр
Свойства правильного тетраэдра:
Объём тетраэдра
где S – площадь любой грани, а H – высота, опущенная на эту грань.
0 & 1 & 1 & 1 & 1 \\ 1 & 0 & d_<12>^2 & d_<13>^2 & d_<14>^2 \\ 1 & d_<12>^2 & 0 & d_<23>^2 & d_<24>^2 \\ 1 & d_<13>^2 & d_<23>^2 & 0 & d_<34>^2 \\ 1 & d_<14>^2 & d_<24>^2 & d_<34>^2 & 0
1 & \cos \gamma & \cos \beta \\ \cos \gamma & 1 & \cos \alpha \\ \cos \beta & \cos \alpha & 1 \end
1 & \cos \gamma \\ \cos \gamma & 1 \\ \end
Тетраэдры в микромире
Тетраэдры в живой природе
Тетраэдры в технике
См. также
Напишите отзыв о статье «Тетраэдр»
Примечания
Литература
Отрывок, характеризующий Тетраэдр
Источники информации:
- http://mnogogranniki.ru/tetraedr.html
- http://handsmake.ru/tetraedr-iz-kartona.html
- http://papermix.ru/raznoe/figury/kak_sdelat_tetrajedr_iz_bumagi_svoimi_rukami.html
- http://slime-recept.com/origami/tetraedr-iz-bumagi-ili-kartona-svoimi-rukami.html
- http://jprosto.ru/kak-sdelat-tetraedr/
- http://newsu.ru/hobbi-i-rukodelie/kak-iz-bumagi-sdelat-tetraedr.html
- http://otvet.ya.guru/questions/1877601-kak-sdelat-tetraedr-iz-bumagi-foto-shemy-video.html
- http://all-origami.ru/piramida-origami/
- http://tamhouse.ru/construction-work/kak-sdelat-pravilnyi-tetraedr-pravilnyi-tetraedr-piramida-kak.html