Как сделать развертку конуса
Как сделать развертку конуса
Построение развертки конуса
Варианты построения развертки:
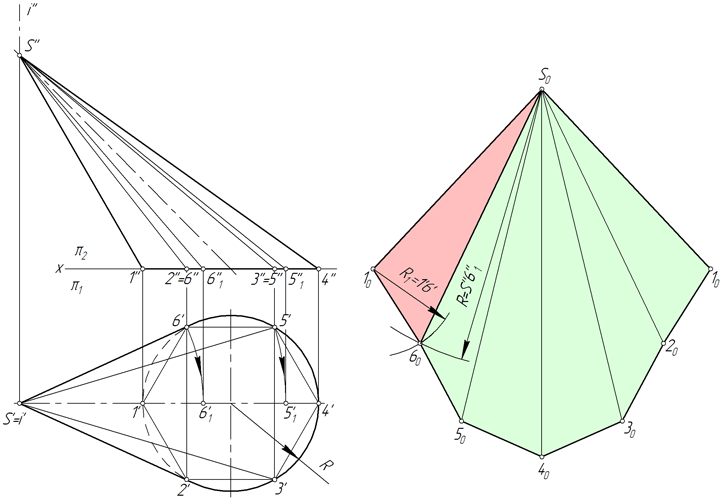
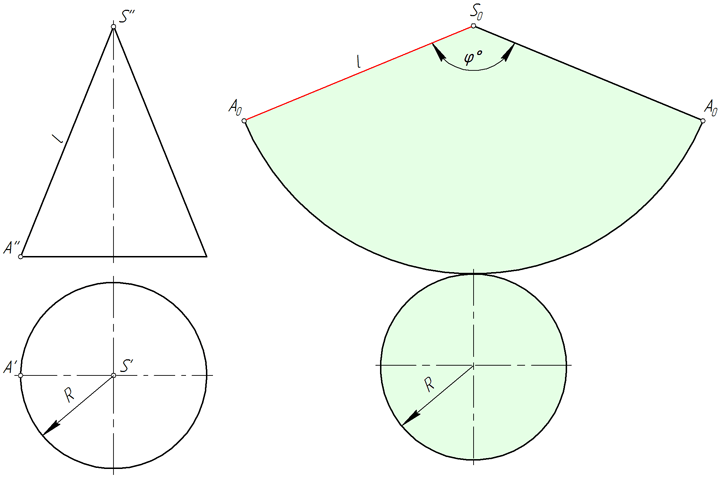
Развертка прямого кругового конуса
Развертка боковой поверхности прямого кругового конуса представляет собой круговой сектор, радиус которого равен длине образующей конической поверхности l, а центральный угол φ определяется по формуле φ=360*R/l, где R – радиус окружности основания конуса.
В ряде задач начертательной геометрии предпочтительным решением является аппроксимация (замена) конуса вписанной в него пирамидой и построение приближенной развертки, на которую удобно наносить линии, лежащие на конической поверхности.
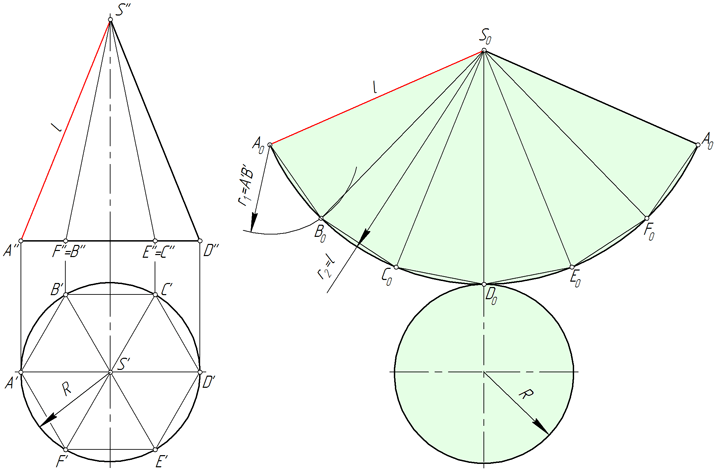
На рисунке ниже в прямой круговой конус вписана правильная шестиугольная пирамида SABCDEF, и приближенная развертка его боковой поверхности состоит из шести равнобедренных треугольников – граней пирамиды.
Рассмотрим треугольник S0A0B0. Длины его сторон S0A0 и S0B0 равны образующей l конической поверхности. Величина A0B0 соответствует длине A’B’. Для построения треугольника S0A0B0 в произвольном месте чертежа откладываем отрезок S0A0=l, после чего из точек S0 и A0 проводим окружности радиусом S0B0=l и A0B0= A’B’ соответственно. Соединяем точку пересечения окружностей B0 с точками A0 и S0.
Точки A, B, C, D, E и F, лежащие в основании конуса, соединяем плавной кривой – дугой окружности, радиус которой равен l.
Развертка наклонного конуса
Рассмотрим порядок построения развертки боковой поверхности наклонного конуса методом аппроксимации (приближения).
Степень соответствия приближенной развертки действительной зависит от количества граней вписанной пирамиды. Число граней выбирают, исходя из удобства чтения чертежа, требований к его точности, наличия характерных точек и линий, которые нужно перенести на развертку.
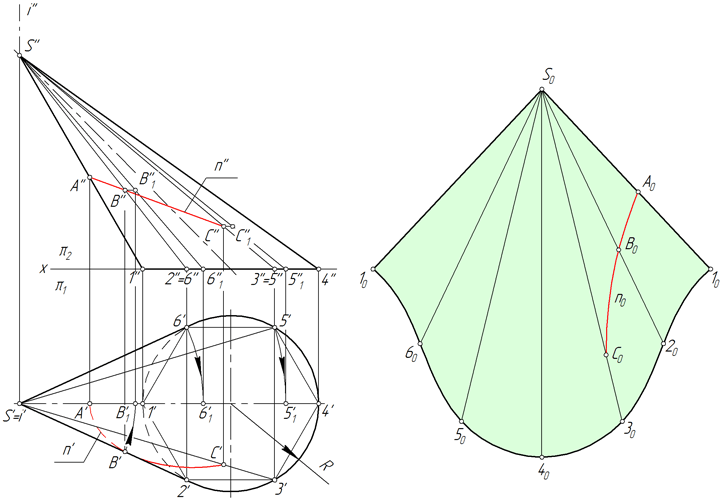
Перенос линии с поверхности конуса на развертку
Линия n, лежащая на поверхности конуса, образована в результате его пересечения с некоторой плоскостью (рисунок ниже). Рассмотрим алгоритм построения линии n на развертке.
Развертка усеченного конуса
Описываемый ниже способ построения развертки прямого кругового усеченного конуса основан на принципе подобия.
Калькуляторы расчета размеров развертки конуса
Иногда в ходе выполнения тех или иных хозяйственных работ мастер встаёт перед проблемой изготовления конуса – полного или усеченного. Это могут быть операции, скажем, с тонким листовым металлом, эластичным пластиком, обычной тканью или даже бумагой или картоном. А задачи встречаются самый разные – изготовление кожухов, переходников с одного диаметра на другой, козырьков или дефлекторов для дымохода или вентиляции, воронок для водостоков, самодельного абажура. А может быть даже просто маскарадного костюма для ребенка или поделок, заданных учителем труда на дом.

Чтобы из плоского материала свернуть объёмную фигуру с заданными параметрами, необходимо вычертить развертку. А для этого требуется рассчитать математически и перенести графически необходимые точные размеры этой плоской фигуры. Как это делается – рассмотрим в настоящей публикации. Помогут нам в этом вопросе калькуляторы расчета размеров развертки конуса.
Калькуляторы расчета размеров развертки конуса
Несколько слов о рассчитываемых параметрах
Понять принцип расчета будет несложно, разобравшись со следующей схемой:
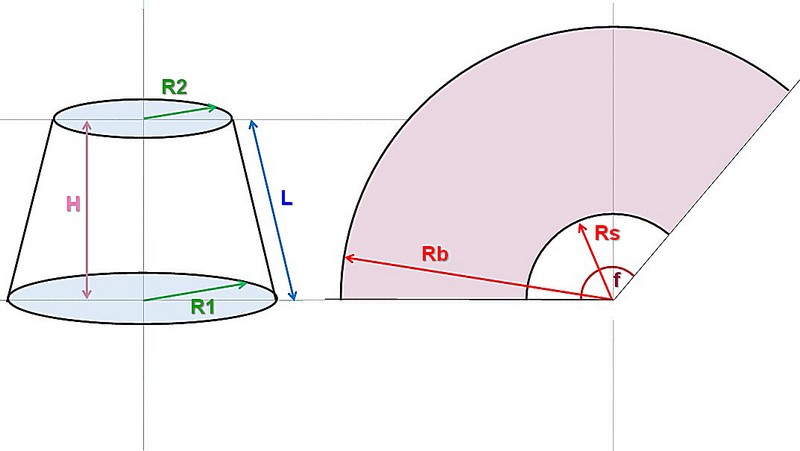
Итак, сам конус определяется радиусами оснований (нижней и верхней окружности) R1 и R2, и высотой Н. Понятно, что если конус не усеченный, то R2 просто равно нулю.
Буквой L обозначена длина боковой стороны (образующей) конуса. Она в некоторых случаях уже известна – например, требуется сделать конус по образцу или выкроить материал для обтяжки уже имеющегося каркаса. Но если она неизвестна – не беда, ее несложно рассчитать.
Справа показана развёртка. Она для усеченного конуса ограничена сектором кольца, образованного двумя дугами, внешней и внутренней, с радиусами Rb и Rs. Для полного конуса Rs также будет равен нулю. Хорошо видно, что Rb = Rs + L
Угловую длину сектора определяет центральный угол f, который в любом случае предстоит рассчитать.
Все расчеты займут буквально минуту, если воспользоваться предлагаемыми калькуляторами:
Шаг 1 – определение длины образующей L
(Если она уже известна – шаг пропускается)
Шаг 2 – определение радиусов внутренней и внешней дуги развертки
Радиусы рассчитываются поочередно – с выбором в соответствующем поле калькулятора.
Что такое развертка конуса и как ее построить? Формулы и пример решения задачи
Каждый школьник слышал о круглом конусе и представляет, как выглядит эта объемная фигура. В данной статье дается определение развертки конуса, приводятся формулы, описывающие ее характеристики, а также описывается способ ее построения с помощью циркуля, транспортира и линейки.
Круглый конус в геометрии
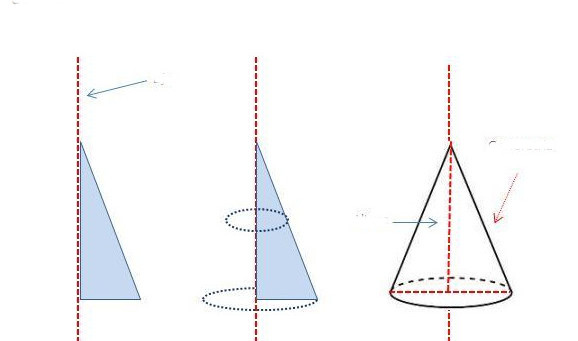
Приведем геометрическое определение этой фигуры. Круглым конусом называется поверхность, которая образована прямыми отрезками, соединяющими все точки некоторой окружности с одной-единственной точкой пространства. Эта единственная точка не должна принадлежать плоскости, в которой лежит окружность. Если вместо окружности взять круг, то указанный способ также приводит к получению конуса.
Круглый конус может быть прямым и наклонным. Обе фигуры показаны ниже на рисунке.

Разница между ними заключается в следующем: если перпендикуляр из вершины конуса падает точно в центр окружности, то конус будет прямым. Для него перпендикуляр, который называется высотой фигуры, является частью его оси. В случае конуса наклонного высота и ось образуют некоторый острый угол.
Ввиду простоты и симметричности фигуры далее будем рассматривать свойства только прямого конуса с круглым основанием.
Получение фигуры с помощью вращения
Перед тем как перейти к рассмотрению развертки поверхности конуса, полезно узнать, как с помощью вращения можно получить эту пространственную фигуру.
Вид развертки конуса
Если у нас имеется бумажный конус, то можно взять ножницы и отрезать от него основание. Затем, коническую поверхность следует разрезать вдоль любой образующей и развернуть ее на плоскости. Таким способом мы получили развертку боковой поверхности конуса. Две поверхности вместе с исходным конусом показаны на схеме ниже.
Внизу справа изображен круг основания. По центру показана развернутая коническая поверхность. Оказывается, что она соответствует некоторому круговому сектору круга, радиус которого равен длине образующей g.
Угол и площадь развертки
Теперь получим формулы, которые по известным параметрам g и r позволяют рассчитать площадь и угол развертки конуса.
Очевидно, что дуга кругового сектора, показанного выше на рисунке, имеет длину, равную длине окружности основания, то есть:
Если бы весь круг радиусом g был построен, то его бы длина составила:
Поскольку длина L соответствует 2*pi радианам, тогда угол, на который опирается дуга l, можно определить из соответствующей пропорции:
Тогда неизвестный угол φ будет равен:
Подставляя выражения для длин l и L, приходим к формуле для угла развертки боковой поверхности конуса:
Угол φ здесь выражен в радианах.
Для определения площади Sb кругового сектора воспользуемся найденным значением φ. Составляем еще одну пропорцию, только уже для площадей. Имеем:
Откуда следует выразить Sb, а затем, подставить значение угла φ. Получаем:
Sb = φ*g2*pi/(2*pi) = 2*pi*r/g*g2/2 = pi*r*g.
Для площади конической поверхности мы получили достаточно компактную формулу. Величина Sb равна произведению трех множителей: числа пи, радиуса фигуры и ее образующей.
Тогда площадь всей поверхности фигуры будет равна сумме Sb и So (площадь круглого основания). Получаем формулу:
S = Sb + So = pi*r*(g + r).
Построение развертки конуса на бумаге
Для выполнения этой задачи понадобится лист бумаги, карандаш, транспортир, линейка и циркуль.
В первую очередь начертим прямоугольный треугольник со сторонами 3 см, 4 см и 5 см. Его вращение вокруг катета в 3 см даст искомый конус. У фигуры r = 3 см, h = 4 см, g = 5 см.
Построение развертки начнем с рисования циркулем окружности радиусом r. Ее длина будет равна 6*pi см. Теперь рядом с ней нарисуем еще одну окружность, но уже радиусом g. Ее длина будет соответствовать 10*pi см. Теперь нам нужно от большой окружности отрезать круговой сектор. Его угол φ равен:
φ = 2*pi*r/g = 2*pi*3/5 = 216o.
Теперь откладываем транспортиром этот угол на окружности с радиусом g и проводим два радиуса, которые будут ограничивать круговой сектор.
Таким образом, мы построили развертку конуса с указанными параметрами радиуса, высоты и образующей.
Пример решения геометрической задачи
Дан круглый прямой конус. Известно, что угол его боковой развертки равен 120o. Необходимо найти радиус и образующую этой фигуры, если известно, что высота h конуса равна 10 см.
Вторым выражением, которое следует использовать при решении, является формула для угла φ:
Таким образом, мы имеем два уравнения, связывающих две неизвестные величины (r и g).
Выражаем из второй формулы g и подставляем результат в первую, получаем:
Угол φ = 120o в радианах равен 2*pi/3. Подставляем это значение, получаем конечные формулы для r и g:
Остается подставить значение высоты и получить ответ на вопрос задачи: r ≈ 3,54 см, g ≈ 10,61 см.
Как сделать конус из бумаги (20 способов)
Конус из бумаги можно назвать самой простой конструкцией. Есть несколько советов как сделать конус из бумаги. Ознакомившись с ними даже, ребенок сможет сделать эту геометрическую фигуру, которая лежит в основе многих изделий.
Как сделать конус из бумаги:
Пошагово показано, как сделать конус из бумаги своими руками с дном. Конус сделан из офисной бумаги формата А4. Точно так же можно сделать конус из ватмана. Здесь представлено изготовление конуса как геометрической фигуры для школьных занятий и для другого использования. Как сделать конус из бумаги пошаговая инструкция.
Нужно помнить — чем больше радиус круга, тем выше получится конус и будет возможность сделать шире его основание.
Как сделать конус из листа бумаги, ватмана или картона своими руками:
Смотрите видео урок о том, как сделать (изготовить) конус из листа офисной бумаги формата А4, ватмана или картона своими руками. Ровный бумажный конус является основой множества поделок — колпака, шляпы, носа, ракеты, елки, деда Мороза. Его можно делать дома с мамой.
Как сделать конус из бумаги? Как сделать геометрические тела вращения? Геометрия:
Как сделать объемный конус из бумаги:
Инструкция, как сделать своими руками объемный конус с дном из бумаги.
Скоро начало школы, встреча с одноклассниками, новые предметы…Но в расписании останется и много старых уроков, а именно математика. Дети учат ее с начальной школы, ведь этот предмет очень тесно связан с нашей повседневной жизнью.
В старших классах дети учат уже и геометрию, где детально изучают фигуры и их свойства.
Поэтому сегодня у нас ролик об одной из самых известных геометрических фигур, а имено речь пойдет о бумажном конусе. Его очень просто сделать даже своими руками. Для этого берем лист бумаги или картона, сворачиваем его в конус, отрезаем нижнюю часть выравнивая края. Прикладываем бумажную основу к листу, делаем насечки и обводим карандашом. Намазав круг клеем приклеиваем дно бумажного конуса, аккуратно обрезаем лишнее и вот наша объемная геометрическая фигура наконец готова.
Как сделать конус из листа бумаги, ватмана или картона своими руками. Основа для елки:
Как сделать конус из бумаги?- Как сделать конус из листа бумаги своими руками? — Конус из бумаги:
Как сделать усечённый конус из бумаги? Усечённый конус из бумаги:
Как сделать конус из бумаги. Основа для елки своими руками #tatabor:
Как сделать конус из бумаги с заранее заданными параметрами:
Усеченный конус из бумаги. Как сделать усеченный конус:
Усеченный конус из бумаги. Как сделать усеченный конус из бумаги:
Как сделать конус своими руками:
Простой расчёт развёртки конуса:
Diy 🎂 — Как сделать колпак на день рождения своими руками:
Конусы для слоеных трубочек: два способа:
Как из бумаги сделать конус:
Как сделать ёлочку. 2 вида. Как сделать конус из бумаги:
Как сделать конус аригами:
Как сделать Конус для хны.Как из бумаги сделать конус. Мехенди.Make Henna Cone♥diy♥Идеи рукоделия:
Конусы из бумаги можно использовать в различных домашних проектах. Нужен острый нос для бумажной ракеты или снеговика? Хотите сделать праздничный колпак? Бумажные конусы обладают огромным потенциалом по части внешнего вида, к тому же их достаточно легко смастерить. Имея готовый конус на руках, вы можете пойти дальше и украсить его на свой вкус.
Конус, как напечатать картинку?
Этот вопрос возникает при сублимационном термотрансфере на конические предметы, например, кружку латте или при прямой печати на сувенирных принтерах.
Fabula Metallic. Печать Фотографий, Постеров, Картин, Табличек На Металле – Подробнее
Бумажный или пластиковый стаканчик
Самый распространенный конический предмет, с которым сталкиваются абсолютно все люди — это стаканчик. Он может быть бумажным или пластиковым, с принтом или без, но неизменным остается одно — это форма! Коническая фома стаканчика была выбрана не просто так, она имеет неоспоримое преимущество перед цилиндрической.
Форма конуса позволяет вставлять один стаканчик в другой, тем самым получается сформировать компактную упаковку из десятков изделий. Форма цилиндра не позволяет этого сделать. Итак, подобная конусообразная форма делает удобнее хранение, транспортировку и реализацию стаканчиков.
Однако, при необходимости напечатать картинку на конусообразном предмете, возникают некоторые технические и дизайнерские сложности. Сразу обращаю ваше внимание, что стаканчик является усеченным конусом, и далее рассматриваемый способ подготовки принта для печати, будет основан именно на построении макета усеченного конуса и подходит для любых подобных предметов, например, для кружек латте.
 Развертка усеченного конуса
Развертка усеченного конуса
Для правильной печати прямоугольного изображения на конусе, нам нужно наложить его на развертку усеченного конуса и деформировать в соответствии со сторонами развертки.
Построение развертки
Есть как минимум два способа построения: ручные расчеты и программные. Для первого способа можно воспользоваться стандартными геометрическими формулами.
Ручной расчет
Программный расчет
Воспользуемся бесплатным сервисом Templatemaker (© Ideogram). Перейдем в раздел Cone (truncated) внесем в поля нужные нам значения.
Построение принта
В векторной программе
Как создать печатное изображение для конических кружек с помощью CorelDRAW
Искажение растровых и векторных объектов для печати кружек латте с помощью Corel Draw 2018 и инструмента “Envelope” (Конверт)
В растровой программе
В специализированных САПР
PACKZ – Warping & 3D Conical cups
Warp artwork on conical labels with Studio

Как сделать восьмигранный конус из оцинкованного листа. Как сделать развертку – выкройку для конуса или усеченного конуса заданных размеров
Калькулятор и формула для вычисления уклона конуса детали.
Уклон конуса может быть определен как отношение разности наибольшего диаметра конуса и наименьшего диаметра конуса к двойной длине конуса, тогда формула для определения уклона конуса детали будет иметь нижеследующий вид:
Также уклон конуса детали можно вычислить как половину конусности детали, такая формула будет следующей:
Либо уклон конуса можно рассчитать как тангенс угла наклона конуса по нижеследующей формуле:
Для определения уклона конуса необходимо ввести значения наибольшего диаметра конуса, наименьшего диаметра конуса, длины конуса и нажать кнопку «ВЫЧИСЛИТЬ.»
Результатом вычисления будет значение уклона конуса.
При проведении инженерных и других расчетах, а также работе с инженерной графикой и создании чертежей приходится создавать уклон. Конусность получила весьма широкое распространение, она применяется при изготовлении самых различных деталей. Показатель конусности рассчитывается в большинстве случаев при создании деталей, которые получили широкое распространение в сфере машиностроения. Рассмотрим основные параметры, особенности начертания и многие другие моменты подробнее.
Значение конусности
Рассматривая конусность следует учитывать, что этот показатель напрямую связан с уклоном. Этот параметр определяет отклонение прямой лини от вертикального ил горизонтального положения. При этом конусность 1:3 или конусность 1:16 существенно отличается. Определение уклона характеризуется следующими особенностями:
Стоит учитывать, что нормальные конусности несколько отличаются от рассматриваемого ранее параметра. Это связано с тем, что конусностью называется соотношение диаметра основания к высоте.
Рассчитать этот показатель можно самым различным образом, наибольшее распространение получила формула K=D/h. В некоторых случаях обозначение проводится в процентах, так как этот переменный показатель применяется для определения всех других параметров.
Рассматривая конусность 1:7 и другой показатель следует также учитывать особенности отображения информации на чертеже. Чаще всего подобное отображение проводится при создании технической документации в машиностроительной области.






Обозначение конусности на чертеже
При создании технической документации должны учитываться все установленные стандарты, так как в противном случае она не может быть использована в дальнейшем. Рассматривая обозначение конусности на чертежах следует уделить внимание следующим моментам:
Простейшее обозначение конусности предусматривает также отображения дополнительных размеров, к примеру, справочную. В некоторых случаях применяется знак конусности, который позволяет сразу понят о разности диаметров.
Выделяют достаточно большое количество различных стандартов, которые касаются обозначения конусности. К особенностям отнесем следующее:


Техника папье-маше
Этот раздел также научит, как сделать конус из бумаги для елки
Большой или маленький вам нужен размер, в данном случае неважно. Заготовка получается прочной и твердой даже без дополнительного каркаса
Этот вариант подойдет тем, у кого нет единого плотного листа для изготовления конуса соответствующего размера.
Для работы этим методом подойдет любая бумага, даже газетная или от старых журналов, однако, потребуется основа-заготовка. Можно воспользоваться пластиковым конусом от детского конструктора (исходная деталь не испортится и вернется на место), пластилином, гипсом, пенопластом. По одному шаблону вы сможете сделать много заготовок из папье-маше. Действуйте так:
Вы узнали, как сделать конус из бумаги для елки. Начинайте с изготовления основы, а затем приступайте к ее декорированию.
Для новогоднего оформления квартиры очень хорошо подходят маленькие ёлочки из подручных материалов. Один из главных плюсов таких ёлочек – простота изготовления и широкое поле для фантазии при их украшении. Кроме того, таких ёлочек можно сделать сразу много – разных по виду и украшению и расставить по всей квартире, таким образом, оригинально украсив её. Проще всего сделать ёлочку-конус из бумаги. На специализированных сайтах есть множество идей украшения таких ёлок, к которым Вы всегда сможете добавить свою авторскую выдумку. При всём разнообразии моделей, основа у всех ёлочек одна – конус из бумаги или картона.
Формула для определения конусности
Провести самостоятельно расчет конусности можно при применении различных формул. Стоит учитывать, что в большинстве случаев показатель указывается в градусах, но может и в процентах – все зависит от конкретного случая. Алгоритм проведения расчетов выглядит следующим образом:
Как ранее было отмечено, конусность 1:5 и другие показатели стандартизированы. Для этого применяется ГОСТ 8593-81.
На чертеже вычисления не отображаются. Как правило, для этого создается дополнительная пояснительная записка. Вычислить основные параметры довольно просто, в некоторых случаях проводится построение чертежа, после чего измеряется значение угла и другие показатели.






Угол конуса
Важным показателем при построении различных чертежей считается угол конуса. Он определяется соотношение большого диаметра к меньшему. Высчитывается этот показатель по следующим причинам:
Как ранее было отмечено, в машиностроительной области показатель стандартизирован. В другой области значение может существенно отличаться от установленных стандартов. Некоторые изделия характеризуются ступенчатым расположение поверхностей. В этом случае провести расчеты достаточно сложно, так как есть промежуточный диаметр.





Такие разные елочки
Красивые елочки, сделанные своими руками, — это отличное решение для украшения дома к празднику, а также для небольшого подарка для близкого человека. Ведь так важно делиться праздничным настроением с другими людьми. Вариантов таких елочек очень много. Елочку из картонного конуса можно предложить сделать деткам. Это занятие придется им по вкусу и поможет реализовать свой творческий потенциал.
Взрослые мастерицы делают великолепные поделки из различной бумаги, декоративных элементов, ниток, мишуры, конфет и даже перьев.
Вдохновились? А теперь внимательно посмотрите на фото всех этих красивых поделок. Что в них общего? Конечно же, это основание в виде конуса. Причем у каждой елочки оно свое. Если елочка предназначена как напольная или настольная композиция, то донышко можно не делать. Но есть и такие поделки, в которых дно конуса должно быть закрыто. О том, как делать конусы из картона для основы таких елочек, читайте ниже.
Что такое уклон?
Как ранее было отмечено, довольно важным показателем можно считать уклон. Он представлен линией, которая расположена под углом к горизонту. Если рассматривать конусность на чертеже, то она представлена сочетанием двух разнонаправленных уклонов, которые объединены между собой.
Понятие уклона получило весьма широкое распространение. В большинстве случаев для его отображения проводится построение треугольника с определенным углом.
Две вспомогательные стороны применяются для расчета угла, которые и определяет особенности наклона основной поверхности.
Роликовые вращатели самоцентрирующиеся INZT 10 E
предлагает свои услуги по вальцовке металла с применением современного высокотехнологичного оборудования. Суть этой технологической операции состоит в холодном деформировании листовых материалов на специальных станках вдоль заданного направления. В процессе вальцевания листа металла он проходит или прокатывается между несколькими валами и происходит его подгибание до требуемого радиуса. Мы обеспечиваем комплексный подход к решению самых разных технических задач заказчика – любого уровня сложности и масштабов. Отличное оснащение производственной площадки, использование станков с ЧПУ и мастерство наших специалистов – все это служит гарантией успеха и высокого качества работ.
Как определить уклон
Для определения уклона достаточно воспользоваться всего одной формулой. Как ранее было отмечено, существенно упростить задачу можно при построении прямоугольного треугольника. Среди особенностей подобной работы отметим следующие моменты:
Формула, которая требуется для вычисления рассматриваемого показателя указывалась выше. Стоит учитывать, что полученный показатель также переводится в градусы.
Пример решения геометрической задачи
Дан круглый прямой конус. Известно, что угол его боковой развертки равен 120o. Необходимо найти радиус и образующую этой фигуры, если известно, что высота h конуса равна 10 см.
Задача не является сложной, если вспомнить, что круглый конус — это фигура вращения прямоугольного треугольника. Из этого треугольника следует однозначная связь между высотой, радиусом и образующей. Запишем соответствующую формулу:
Вторым выражением, которое следует использовать при решении, является формула для угла φ:
Таким образом, мы имеем два уравнения, связывающих две неизвестные величины (r и g).
Выражаем из второй формулы g и подставляем результат в первую, получаем:
Угол φ = 120o в радианах равен 2*pi/3. Подставляем это значение, получаем конечные формулы для r и g:
Остается подставить значение высоты и получить ответ на вопрос задачи: r ≈ 3,54 см, g ≈ 10,61 см.
Особенности построения уклона и конусности
Область черчения развивалась на протяжении достаточно длительного периода. Она уже много столетий назад применялась для передачи накопленных знаний и навыков. Сегодня изготовление всех изделия может проводится исключительно при применении чертежей. При этом ему больше всего внимания уделяется при наладке массового производства. За длительный период развития черчения были разработаны стандарты, которые позволяют существенно повысить степень читаемости всей информации. Примером можно назвать ГОСТ 8593-81. Он во многом характеризует конусность и уклон, применяемые методы для их отображения. Начертательная геометрия применяется для изучения современной науки, а также создания различной техники. Кроме этого, были разработаны самые различные таблицы соответствия, которые могут применяться при проведении непосредственных расчетов.
Построение уклона и конусности
Провести построение уклона и конусности достаточно просто, только в некоторых случаях могут возникнуть серьезные проблемы. Среди основных рекомендаций отметим следующее:
На сегодняшний день, когда компьютеры получили весьма широкое распространение, отображение чертежей также проводится при применении специальных программ. Их преимуществами можно назвать следующее:
Процедура построения при применении подобных программ характеризуется достаточно большим количеством особенностей, которые нужно учитывать. Основными можно назвать следующее:
Услуги вальцовки недорого
Компания предоставляет услуги вальцовки по ценам
, наиболее приемлемым в Москве. На заказ мы качественно выполним любые объемы работ, в том числе в промышленных масштабах. Изготовим изделия в точности, соответствующие чертежам заказчика. Работы выполняются в оговоренные сроки, без нарушения графиков. Для вальцовки у нас имеется технологически современное оборудование и опытные специалисты, которые относятся к своей работе с максимальной степенью ответственности. Производим вальцевание тонколистового и пруткового металла. Осуществляем вальцовку кромок листа и углов с точным радиусом закругления.
Что такое уклон? Как определить уклон? Как построить уклон? Обозначение уклона на чертежах по ГОСТ.
Уклон. Уклон это отклонение прямой линии от вертикального или горизонтального положения. Определение уклона. Уклон определяется как отношение противолежащего катета угла прямоугольного треугольника к прилежащему катету, то есть он выражается тангенсом угла а. Уклон можно посчитать по формуле i=AC/AB=tga.
Построение уклона. На примере (рисунок ) наглядно продемонстрировано построение уклона. Для построения уклона 1:1, например, нужно на сторонах прямого угла отложить произвольные, но равные отрезки. Такой уклон, будет соответствовать углу в 45 градусов. Для того чтобы построить уклон 1:2, нужно по горизонтали отложить отрезок равный по значению двум отрезкам отложенным по вертикали. Как видно из чертежа, уклон есть отношение катета противолежащего к катету прилежащему, т. е. он выражается тангенсом угла а.
Обозначение уклона на чертежах. Обозначение уклонов на чертеже выполняется в соответствии с ГОСТ 2.307—68. На чертеже указывают величину уклона с помощью линии-выноски. На полке линии-выноски наносят знак и величину уклона. Знак уклона должен соответствовать уклону определяемой линии, то есть одна из прямых знака уклона должна быть горизонтальна, а другая должна быть наклонена в ту же сторону, что и определяемая линия уклона. Угол уклона линии знака примерно 30°.
Какие поделки можно сделать?
С помощью обычного конуса можно придумать множество интересных поделок к любому празднику, на подарок и просто для украшения интерьера.
Для начала, готовую геометрическую фигуру нужно обклеить скотчем. Затем вязальные (или обычные толстые нити) намазать клеем и, делая круговые движения, наматывать на конус в произвольном порядке.
После того, как клей высохнет нужно будет аккуратно отсоединить конус от ниток и вытащить его. Получился необычный каркас, который затем украшается бусинами, снежинками, звездочками, маленькими шариками, серпантином или дождиком.
Чтобы сделать такую елочку, конус обклеивается цветной бумагой или красивой тканью, добавляются различные крашения сверху, приклеивается звезда на вершину.
Замечательный пакетик делается так:
В такой пакетик можно положить маленькую мягкую игрушку, сладости и т.д. Вверху завязать ленточку и преподнести своим друзьям и родственникам.
По такому же принципу, сделав основу-конус, можно сделать множество других интересных вещей. Некоторые идеи представлены ниже.









Что такое конусность? Формула для расчёта конусности. Обозначение конусности на чертежах.
Конусность. Конусностью называется отношение диаметра основания конуса к высоте. Конусность рассчитывается по формуле К=D/h, где D – диаметр основания конуса, h – высота. Если конус усеченный, то конусность рассчитывается как отношение разности диаметров усеченного конуса к его высоте. В случае усечённого конуса, формула конусности будет иметь вид: К = (D-d)/h.
Размеры стандартизованных конусов не нужно указывать на чертеже. Достаточно на чертеже привести условное обозначение конусности по соответствующему стандарту.
Конусность, как и уклон, может быть указана в градусах, дробью (простой, в виде отношения двух чисел или десятичной), в процентах. Например, конусность 1:5 может быть также обозначена как отношение 1:5, 11°25’16», десятичной дробью 0,2 и в процентах 20. Для конусов, которые применяются в машиностроении, OCT/BKC 7652 устанавливает ряд нормальных конусностей. Нормальные конусности — 1:3; 1:5; 1:8; 1:10; 1:15; 1:20; 1:30; 1:50; 1:100; 1:200. Также в могут быть использованы — 30, 45, 60, 75, 90 и 120°.
Видео гибки конусной обечайки
После сборки проверяется сварочный зазор и выполняются сварочные прихватки (рис.21). Параметры прихваток приведены в таблице 2. Заходные и выводные планки применяются для обеспечения качественного сварного шва по торцам обечайки.
При сборке обечаек используются роликовые стенды (рис.22) и кантователи. Сварку кольцевых и продольных швов обечаек производят ручным способом, механизированным способом или с применением сварочных роботов. Для ликвидации остаточных напряжений в сварных швах обечайки подвергают термообработке в шахтных печах. После сварки производится калибровка обечайки на вальцах — прокатка ее в несколько заходов. При окончательном контроле изготовленных обечаек проверяют их геометрические размеры, отсутствие деформаций и поверхностных дефектов детали.
Установлен сертификат профессионализма, соответствующий занятию промышленного кипятильника, профессиональной семьи тяжелой промышленности и металлических конструкций, который будет иметь официальный характер и действительность на всей территории страны.
Сертификат профессионализма. Аккредитация учебного контракта. Только переходное положение. Адаптация к национальному учебному и профессиональному плану внедрения. Министр труда и социальных дел настоящим уполномочен издавать такие положения, которые могут потребоваться для осуществления этого Королевского указ.
Более подробно об изготовлении отдельных видов обечаек, читайте в разделах «Вентиляция», «Водосток» и «Для гибки металла».
Вальцовка обечаек – важнейший технологический процесс, без которого нельзя даже представить производство цилиндрических деталей. Рассмотрим более подробно его особенности, технологию и используемый инструмент.
Этот Королевский указ вступает в силу на следующий день после его опубликования в Официальном государственном бюллетене. В Мадриде 24 января. Министр труда и социальных дел. Профессиональный профиль профессии. Для строительства различных элементов используются режущие и формовочные машины, а также электросварочное оборудование, а также организует рабочее оборудование для получения продуктов в условиях безопасности и требуемых качественных характеристик. Построить металлические конструкции.
Построить наборы цилиндрических каналов. Компетентность 1: сборка металлоконструкций. Компетентность 2: построение наборов цилиндрических трубопроводов. Компетентность 3: построение конусов и бункеров. Наблюдение при формовании в горячем состоянии не превышает предельную температуру молекулярной структуры материала.
Построение развертки конуса
Круглый конус в геометрии
Приведем геометрическое определение этой фигуры. Круглым конусом называется поверхность, которая образована прямыми отрезками, соединяющими все точки некоторой окружности с одной-единственной точкой пространства. Эта единственная точка не должна принадлежать плоскости, в которой лежит окружность. Если вместо окружности взять круг, то указанный способ также приводит к получению конуса.
Вам будет интересно:Юридический колледж в Иваново: специальности, приемная комиссия, отзывы
Круг называется основанием фигуры, его окружность — это директриса. Отрезки, соединяющие точку с директрисой, называются генератрисами или образующими, а точка, где они пересекаются — это вершина конуса.
Круглый конус может быть прямым и наклонным. Обе фигуры показаны ниже на рисунке.
Разница между ними заключается в следующем: если перпендикуляр из вершины конуса падает точно в центр окружности, то конус будет прямым. Для него перпендикуляр, который называется высотой фигуры, является частью его оси. В случае конуса наклонного высота и ось образуют некоторый острый угол.
Ввиду простоты и симметричности фигуры далее будем рассматривать свойства только прямого конуса с круглым основанием.
Для чего используется конус
Мы подробно разобрали самые простые варианты как сделать правильный конус из бумаги. Для чего используется эта поделка? Направления у нее самые различные:
Ваша фантазия подскажет вам, где еще может применяться конус. А мы поможем вам вдохновиться с помощью простой конусной поделки елочки.




Для нее потребуется:
В основе изделия, как вы уже поняли, лежит конус. Изготовьте его по одной из предложенных выше инструкций.
Далее работаем по схеме:
В ёлке можно сделать отверстия. И если она достаточно широка, поместите внутрь конуса новогодние огоньки. В темноте, они будут приятно мелькать, создавая приятную атмосферу.
Получение фигуры с помощью вращения
Перед тем как перейти к рассмотрению развертки поверхности конуса, полезно узнать, как с помощью вращения можно получить эту пространственную фигуру.
Предположим, что у нас имеется прямоугольный треугольник со сторонами a, b, c. Первые две из них являются катетами, c — это гипотенуза. Поставим треугольник на катет a и начнем его вращать вокруг катета b. Гипотенуза c при этом опишет коническую поверхность. Эта простая методика получения конуса изображена ниже на схеме.
Очевидно, что катет a будет радиусом основания фигуры, катет b — его высотой, а гипотенуза c соответствует образующей круглого прямого конуса.
Создаем новогоднюю елку
Из готового бумажного конуса можно создать отличное новогоднее украшение в виде елочки. Материалы при этом используются самые разнообразные, но общая система изготовления остается общей.
Для создания новогодней елочки можно воспользоваться совершенно другой техникой. На помощь придет папье-маше, с помощью которой можно тоже сделать бумажный конус. Конечно, материала и времени потребуется гораздо больше, но и готовая конструкция получится прочной и статной.
Остается лишь склеить разрезанные половинки обратно, и можно приступать к декорированию будущей елки. Например, её реально покрасить или обмотать нитками, как на фото ниже. Такая схема позволит создать любые варианты елочек, в зависимости от желания и имеющейся основы.
Вид развертки конуса
Как можно догадаться, конус образован двумя типами поверхностей. Одна из них — это плоский круг основания. Предположим, что он имеет радиус r. Вторая поверхность является боковой и называется конической. Пусть ее образующая будет равна g.
Вам будет интересно:Термофильные бактерии: польза и вред для человека
Если у нас имеется бумажный конус, то можно взять ножницы и отрезать от него основание. Затем, коническую поверхность следует разрезать вдоль любой образующей и развернуть ее на плоскости. Таким способом мы получили развертку боковой поверхности конуса. Две поверхности вместе с исходным конусом показаны на схеме ниже.
Внизу справа изображен круг основания. По центру показана развернутая коническая поверхность. Оказывается, что она соответствует некоторому круговому сектору круга, радиус которого равен длине образующей g.










Как сделать конус для елки своими руками?
Для изготовления такой ели потребуется картон, обычная и цветная бумага, ножницы и клей. И разумеется — побольше фантазии. Наилучший материал для изготовления конуса-основы для ёлки – картон. Только для маленьких нежных и воздушных ёлочек, конус можно делать из бумаги.
Конус сворачивается двумя способами
После этого можно делать «хвою» или «ветки» любым выбранным способом, а затем украшать гирляндами лампочек, маленькими игрушками и т.д. Такие ёлочки подходят не только для украшения дома, но и для новогоднего подарка.
Видео
Одним из главных атрибутов такого праздника, как Новый год, является елка. Традиционно елку украшают мишурой, игрушками, но можно также сделать оригинальную картонную елку. Выполняется такая елка достаточно просто, главное — правильно сформировать картонную основу в виде конуса, к тому же такая ель не обязательно должна быть новогодней, она может вписаться в интерьер любого помещения в качестве элемента декора.
В данной статье будут представлены инструкции, как сделать картонный конус для елки. Также будут описаны различные варианты декорирования.
Угол и площадь развертки
Теперь получим формулы, которые по известным параметрам g и r позволяют рассчитать площадь и угол развертки конуса.
Очевидно, что дуга кругового сектора, показанного выше на рисунке, имеет длину, равную длине окружности основания, то есть:
Если бы весь круг радиусом g был построен, то его бы длина составила:
Поскольку длина L соответствует 2*pi радианам, тогда угол, на который опирается дуга l, можно определить из соответствующей пропорции:
Тогда неизвестный угол φ будет равен:
Подставляя выражения для длин l и L, приходим к формуле для угла развертки боковой поверхности конуса:
Угол φ здесь выражен в радианах.
Для определения площади Sb кругового сектора воспользуемся найденным значением φ. Составляем еще одну пропорцию, только уже для площадей. Имеем:
Откуда следует выразить Sb, а затем, подставить значение угла φ. Получаем:
Sb = φ*g2*pi/(2*pi) = 2*pi*r/g*g2/2 = pi*r*g.
Для площади конической поверхности мы получили достаточно компактную формулу. Величина Sb равна произведению трех множителей: числа пи, радиуса фигуры и ее образующей.
Тогда площадь всей поверхности фигуры будет равна сумме Sb и So (площадь круглого основания). Получаем формулу:
S = Sb + So = pi*r*(g + r).
Развертка (выкройка) конуса
Построение развертки конуса на бумаге
Для выполнения этой задачи понадобится лист бумаги, карандаш, транспортир, линейка и циркуль.
В первую очередь начертим прямоугольный треугольник со сторонами 3 см, 4 см и 5 см. Его вращение вокруг катета в 3 см даст искомый конус. У фигуры r = 3 см, h = 4 см, g = 5 см.
Построение развертки начнем с рисования циркулем окружности радиусом r. Ее длина будет равна 6*pi см. Теперь рядом с ней нарисуем еще одну окружность, но уже радиусом g. Ее длина будет соответствовать 10*pi см. Теперь нам нужно от большой окружности отрезать круговой сектор. Его угол φ равен:
φ = 2*pi*r/g = 2*pi*3/5 = 216o.
Теперь откладываем транспортиром этот угол на окружности с радиусом g и проводим два радиуса, которые будут ограничивать круговой сектор.
Таким образом, мы построили развертку конуса с указанными параметрами радиуса, высоты и образующей.
Как сделать конус из бумаги А4
Детали каких-либо изделий иногда имеют форму конуса. Людям, которые не умеют делать конус, это доставляет лишние хлопоты (например, поиск пошаговых инструкций или же просмотр видео-уроков). Этот пункт статьи поможет вам раз и навсегда запомнить, как же всё-таки сделать такую необычную фигуру.
Приступим к работе:
Объём конуса
Конус и его сечение плоскостью
Перу древнегреческого математика Аполлония Пергского принадлежит теоретический труд «Конические сечения». Благодаря его работам в геометрии появились определения кривых: параболы, эллипса, гиперболы. Рассмотрим, причем здесь конус.
Возьмем прямой круговой конус. Если плоскость пересекает его перпендикулярно оси, то в разрезе образуется круг. Когда секущая пересекает конус под углом к оси, то в разрезе получается эллипс.
Секущая плоскость, перпендикулярная основанию и параллельная оси конуса, образует на поверхности гиперболу. Плоскость, разрезающая конус под углом к основанию и параллельная касательной к конусу, создает на поверхности кривую, которую назвали параболой.
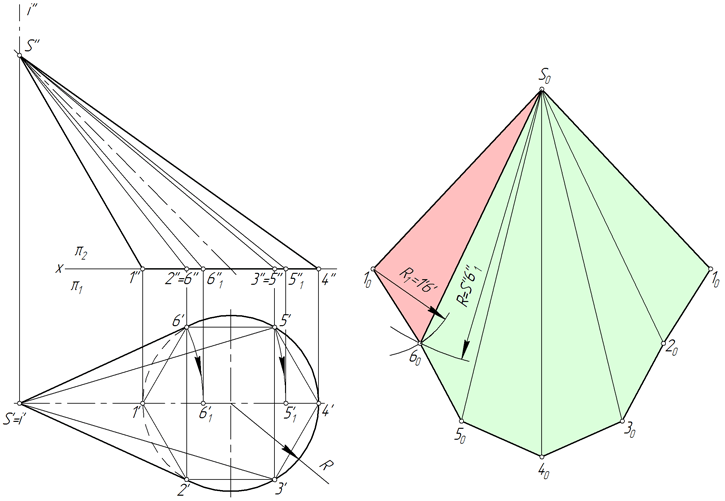
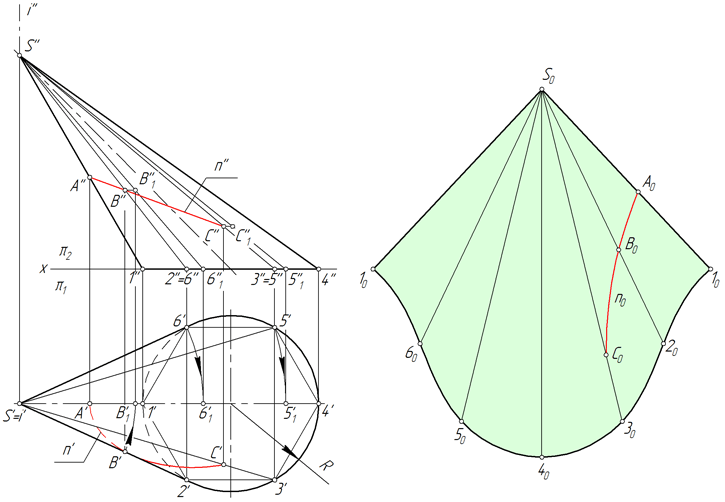
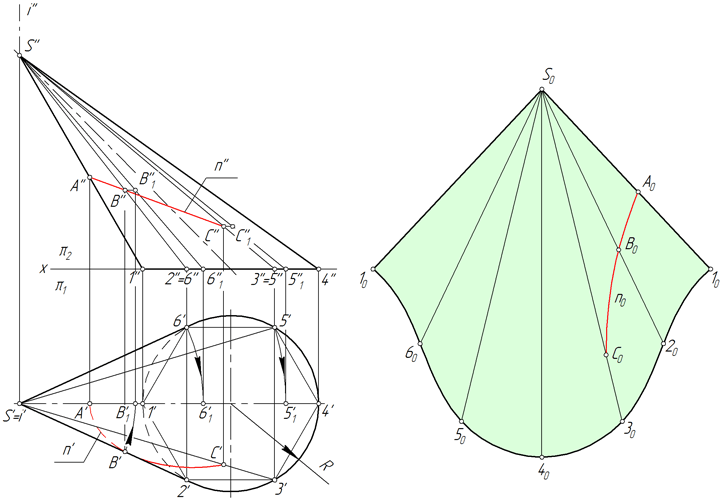
Развертка наклонного конуса
Рассмотрим порядок построения развертки боковой поверхности наклонного конуса методом аппроксимации (приближения).
Степень соответствия приближенной развертки действительной зависит от количества граней вписанной пирамиды. Число граней выбирают, исходя из удобства чтения чертежа, требований к его точности, наличия характерных точек и линий, которые нужно перенести на развертку.
Перенос линии с поверхности конуса на развертку
Линия n, лежащая на поверхности конуса, образована в результате его пересечения с некоторой плоскостью (рисунок ниже). Рассмотрим алгоритм построения линии n на развертке.
Что ещё можно сделать из бумажного конуса?
Бумажную заготовку для конуса можно использовать, чтобы сделать упаковку для сладкого подарка. Для этого на края, с внутренней стороны, добавляют кусочки двустороннего скотча, или же просто промазывают клеем.
Затем на эти участки помещаются листы гофрированной бумаги.
Бумажный конус можно использовать и для других поделок. Например, если делать его из плотного картона, то затем, с помощью ткани, получится создать вот такие игрушки животных или елочное украшение.
Построение развёртки цилиндра[править]
Цилиндрправить
Тело вращения с наиболее простой развёрткой, имеющей форму прямоугольника, где две параллельные стороны соответствуют высоте цилиндра, а две другие параллельные стороны — длине окружности оснований цилиндра.
Усечённый цилиндр (рыбина)править
Подобным образом строятся любые цилиндрические срезы. Примечание: Почему «Рыбина» — если продолжить построение развёртки, при этом половину построить от точки D, а вторую в обратную сторону от вертикали BC, то получившийся рисунок, будет похож на рыбку, или рыбий хвост.
Чертёж: «Усечённый цилиндр»
Основы и инструмент[править]
> — Число Пи (Pi),
Как правило, для вычисления используется значение Π <\displaystyle \Pi
> (Pi) до второго знака (3,14), но в некоторых случаях, этого может быть недостаточно.
Представленный в статье материал, подразумевает, что вы имеете представление об основах черчения, умеете делить окружность, находить центр отрезка при помощи циркуля, снимать/переносить размеры циркулем, пользоваться лекалами, и соответствующим справочным материалом. Потому, объяснение многих моментов в статье опущено.
Уклоны и конусность — Техническое черчение
Если требуется через точку Л, лежащую на прямой AB (фиг. 57, в), провести прямую с уклоном i=l:n относительно AB, надо отложить от точки А по направлению данной прямой n произвольных единиц; в конце полученного отрезка AB восстановить перпендикуляр ЕС длиной в одну такую же единицу. Гипотенуза AС построенного прямоугольного треугольника определяет искомую прямую.
2) опустить из точки M перпендикуляр ME на прямую AВ и принять его за единицу. По направлению прямой AB влево или вправо от точки E отложить n таких же отрезков; гипотенузы DM или MD1 построенных таким образом прямоугольных треугольников являются искомыми прямыми.
Построение конусности l:n относительно данной оси сводится к построению уклонов l:n/2 с каждой стороны оси.
Уклон или конусность чаще всего указывается в процентах или отношением единицы к целому числу. Рассмотрим эти способы построения на примерах.
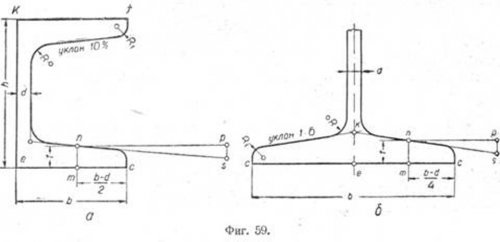
Пример 1. Требуется построить профиль сечения швеллера № 5 ОСТ 10017-39 (фиг. 59, а), если известно, что уклон его полок равен 10%
Размеры для построения берём из ОСТ 10017-39.
Проводим вертикальную прямую ek, равную h = 50 мм. Из точек e и k проводим прямые ec и kf, равные ширине полки b = 37 мм.
Ввиду того, что обе полки швеллера одинаковы, ограничимся построением только одной из них. Откладываем на прямой ec от точки с отрезок cm, равный (b-d)/2.
В точке m на перпендикуляре к прямой ec откладываем отрезок mn, равный t = 7 мм. Через точку n проводим прямую np параллельно ec, равную 50 мм.
Прямая sn является искомой прямой, имеющей уклон 10% по отношению к ec. Дальнейшее построение профиля не представляет затруднений.
Отрезок np можно взять любой длины. Чем больше его величина, тем точнее будет построена прямая уклона. Однако для удобства вычисления следует принимать отрезок np таким, чтобы длина его, выражаемая в миллиметрах, оканчивалась на 0 или 5.
П p и м e p 2. Построить профиль сечения двутавра № 10 ОСТ 10016-39 (фиг. 59, б), если известно, что уклон полок его равен 1:6. Размеры для построения берём из ОСТ 10016-39.
Проводим горизонтальную прямую cc, равную ширине полки b = = 68 мм. Через точку e, являющуюся серединой ширины полки, проводим вертикальную линию. Откладываем от точки с отрезок mс, равный
(b-d)/4. В точке m, перпендикулярно к отрезку cc, проводим прямую и
на ней откладываем отрезок mn, равный t=6,5 мм. Через точку n проводим горизонтальную прямую np, равную 30 мм, которая будет служить катетом прямоугольного треугольника. Чем длиннее катет, тем точнее будет построен уклон. Для удобства принимают длину отрезка np кратной шести, тогда второй катет будет равен целому числу. Величина второго катета определяется из формулы
Откладываем в точке p под углом 90° к прямой np вычисленную длину второго катета, получим точку 5. Проводим через точки s и n прямую, которая и будет соответствовать искомой прямой, имеющей уклон 1 :6.
Построение сопряжений такое же, как и для швеллера в предыдущем примере.
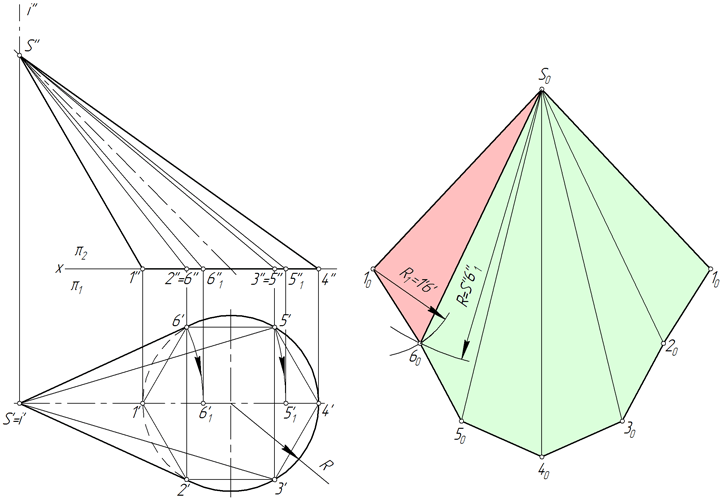
Развертка прямого кругового конуса
Развертка боковой поверхности прямого кругового конуса представляет собой круговой сектор, радиус которого равен длине образующей конической поверхности l, а центральный угол φ определяется по формуле φ=360*R/l, где R – радиус окружности основания конуса.
В ряде задач начертательной геометрии предпочтительным решением является аппроксимация (замена) конуса вписанной в него пирамидой и построение приближенной развертки, на которую удобно наносить линии, лежащие на конической поверхности.
На рисунке ниже в прямой круговой конус вписана правильная шестиугольная пирамида SABCDEF, и приближенная развертка его боковой поверхности состоит из шести равнобедренных треугольников – граней пирамиды.
Рассмотрим треугольник SAB. Длины его сторон SA и SB равны образующей l конической поверхности. Величина AB соответствует длине A’B’. Для построения треугольника SAB в произвольном месте чертежа откладываем отрезок SA=l, после чего из точек S и A проводим окружности радиусом SB=l и AB= A’B’ соответственно. Соединяем точку пересечения окружностей B с точками A и S.
Точки A, B, C, D, E и F, лежащие в основании конуса, соединяем плавной кривой – дугой окружности, радиус которой равен l.
Определение диаметра через объем и высоту
Теперь покажем, как найти диаметр конуса, зная его объем V и высоту h. Для этого необходимо вспомнить, что объем конуса, как и объем любой пирамиды, можно определить, пользуясь следующим равенством:
Здесь S — площадь основания. Поскольку площадь основания в рассматриваемом случае является площадью круга, то это выражение можно переписать в таком виде:
Остается выразить отсюда радиус и умножить его в два раза, и мы получим ответ на вопрос о том, как найти диаметр конуса через величины V и h. Имеем:
Заметим, что в правой части получается размерность длины. Это доказывает правильность полученной формулы.
Все записанные в статье формулы для диаметра d фигуры также являются справедливыми для радиуса, который будет в два раза меньше диаметра.
1 Область применения
Настоящий стандарт распространяется на применяемые в машиностроении конусности и углы конусов гладких конических элементов деталей и устанавливает ряды нормальных конусностей от 1:0,289 до 1:500 и углов конусов от 0,114° до 120°.
Настоящий стандарт не распространяется на конусности и углы конусов, связанные расчетными зависимостями с другими принятыми размерами, негладкие конические элементы деталей (призматические элементы, конические резьбы, конические зубчатые передачи и т.д.).
Правила указания размеров и допусков конических поверхностей на чертежах согласно ГОСТ 2.320.
Решение задачи
Даже простая задача о том, как изготовить ведро определенного объема, требует знаний. Например, необходимо рассчитать размеры ведра, чтобы оно имело объем 10 литров.
Развертка конуса имеет вид, схематически приведенный на рисунке 3.
L — образующая конуса.
Чтобы узнать площадь поверхности ведра, которая вычисляется по следующей формуле:
необходимо вычислить образующую. Ее находим из величины объема V=n*(R12+R22+R1*R2)*H/3.
Усеченный конус образуется вращением прямоугольной трапеции, в которой боковая сторона является образующей конуса.
Теперь у нас имеются все данные, чтобы построить чертеж ведра.
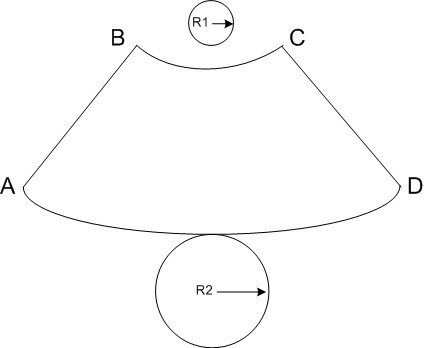
Калькуляторы расчета размеров развертки конуса
Несколько слов о рассчитываемых параметрах
Понять принцип расчета будет несложно, разобравшись со следующей схемой:
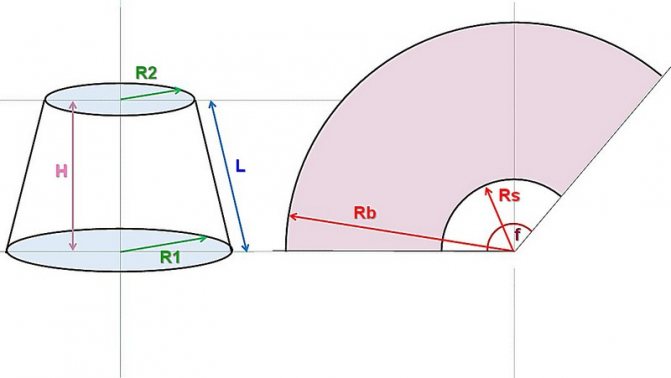
Усеченный конус с определяющими размерами и его развёртка. Показан усеченный конус, но с полным — принцип не меняется, а расчеты и построение становятся даже проще.
Итак, сам конус определяется радиусами оснований (нижней и верхней окружности) R1 и R2, и высотой Н. Понятно, что если конус не усеченный, то R2 просто равно нулю.
Буквой L обозначена длина боковой стороны (образующей) конуса. Она в некоторых случаях уже известна – например, требуется сделать конус по образцу или выкроить материал для обтяжки уже имеющегося каркаса. Но если она неизвестна – не беда, ее несложно рассчитать.
Справа показана развёртка. Она для усеченного конуса ограничена сектором кольца, образованного двумя дугами, внешней и внутренней, с радиусами Rb и Rs. Для полного конуса Rs также будет равен нулю. Хорошо видно, что Rb = Rs + L
Угловую длину сектора определяет центральный угол f, который в любом случае предстоит рассчитать.
Все расчеты займут буквально минуту, если воспользоваться предлагаемыми калькуляторами:
Развертка наклонного конуса
Рассмотрим порядок построения развертки боковой поверхности наклонного конуса методом аппроксимации (приближения).
Степень соответствия приближенной развертки действительной зависит от количества граней вписанной пирамиды. Число граней выбирают, исходя из удобства чтения чертежа, требований к его точности, наличия характерных точек и линий, которые нужно перенести на развертку.
Перенос линии с поверхности конуса на развертку
Линия n, лежащая на поверхности конуса, образована в результате его пересечения с некоторой плоскостью (рисунок ниже). Рассмотрим алгоритм построения линии n на развертке.
Решение задачи
Даже простая задача о том, как изготовить ведро определенного объема, требует знаний. Например, необходимо рассчитать размеры ведра, чтобы оно имело объем 10 литров.
Развертка конуса имеет вид, схематически приведенный на рисунке 3.
L — образующая конуса.
Чтобы узнать площадь поверхности ведра, которая вычисляется по следующей формуле:
необходимо вычислить образующую. Ее находим из величины объема V=n*(R1 2 +R2 2 +R1*R2)*H/3.
Усеченный конус образуется вращением прямоугольной трапеции, в которой боковая сторона является образующей конуса.
Теперь у нас имеются все данные, чтобы построить чертеж ведра.
Основные определения
Прямой круговой конус образован вращением прямоугольного треугольника вокруг одного катета. Как видно, понятие конуса не изменилось со времен Евклида.
Гипотенуза AS прямоугольного треугольника AOS при вращении вокруг катета OS образует боковую поверхность конуса, поэтому называется образующей. Катет OS треугольника превращается одновременно в высоту конуса и его ось. Точка S становится вершиной конуса. Катет AO, описав круг (основание), превратился в радиус конуса.
Если сверху провести плоскость через вершину и ось конуса, то можно увидеть, что полученное осевое сечение представляет собой равнобедренный треугольник, в котором ось является высотой треугольника.
Также часто требуется рассчитать площадь боковой поверхности тела вращения. Площадь боковой поверхности конуса равна произведению половины длины окружности основания и образующей конуса.
где C — длина окружности основания, l — длина образующей конуса, R — радиус основания.
Формула для определения конусности
Провести самостоятельно расчет конусности можно при применении различных формул. Стоит учитывать, что в большинстве случаев показатель указывается в градусах, но может и в процентах – все зависит от конкретного случая. Алгоритм проведения расчетов выглядит следующим образом:
Как ранее было отмечено, конусность 1:5 и другие показатели стандартизированы. Для этого применяется ГОСТ 8593-81.
На чертеже вычисления не отображаются. Как правило, для этого создается дополнительная пояснительная записка. Вычислить основные параметры довольно просто, в некоторых случаях проводится построение чертежа, после чего измеряется значение угла и другие показатели.
Развертка наклонного конуса
Рассмотрим порядок построения развертки боковой поверхности наклонного конуса методом аппроксимации (приближения).
Степень соответствия приближенной развертки действительной зависит от количества граней вписанной пирамиды. Число граней выбирают, исходя из удобства чтения чертежа, требований к его точности, наличия характерных точек и линий, которые нужно перенести на развертку.
Перенос линии с поверхности конуса на развертку
Линия n, лежащая на поверхности конуса, образована в результате его пересечения с некоторой плоскостью (рисунок ниже). Рассмотрим алгоритм построения линии n на развертке.
Получение фигуры с помощью вращения
Перед тем как перейти к рассмотрению развертки поверхности конуса, полезно узнать, как с помощью вращения можно получить эту пространственную фигуру.
Предположим, что у нас имеется прямоугольный треугольник со сторонами a, b, c. Первые две из них являются катетами, c — это гипотенуза. Поставим треугольник на катет a и начнем его вращать вокруг катета b. Гипотенуза c при этом опишет коническую поверхность. Эта простая методика получения конуса изображена ниже на схеме.
Очевидно, что катет a будет радиусом основания фигуры, катет b — его высотой, а гипотенуза c соответствует образующей круглого прямого конуса.
Особенности построения уклона и конусности
Область черчения развивалась на протяжении достаточно длительного периода. Она уже много столетий назад применялась для передачи накопленных знаний и навыков. Сегодня изготовление всех изделия может проводится исключительно при применении чертежей. При этом ему больше всего внимания уделяется при наладке массового производства. За длительный период развития черчения были разработаны стандарты, которые позволяют существенно повысить степень читаемости всей информации. Примером можно назвать ГОСТ 8593-81. Он во многом характеризует конусность и уклон, применяемые методы для их отображения. Начертательная геометрия применяется для изучения современной науки, а также создания различной техники. Кроме этого, были разработаны самые различные таблицы соответствия, которые могут применяться при проведении непосредственных расчетов.
Различные понятия, к примеру, сопряжение, уклон и конусность отображаются определенным образом. При этом учитывается область применения разрабатываемой технической документации и многие другие моменты.
К особенностям построения угла и конусности можно отнести следующие моменты:
В целом можно сказать, что основные стандарты учитываются специалистом при непосредственном проведении работы по построению чертежа.
В проектной документации, в которой зачастую отображается конусность, при необходимости дополнительная информация выводится в отдельную таблицу.
Развертка наклонного конуса
Рассмотрим порядок построения развертки боковой поверхности наклонного конуса методом аппроксимации (приближения).
Степень соответствия приближенной развертки действительной зависит от количества граней вписанной пирамиды. Число граней выбирают, исходя из удобства чтения чертежа, требований к его точности, наличия характерных точек и линий, которые нужно перенести на развертку.
Перенос линии с поверхности конуса на развертку
Линия n, лежащая на поверхности конуса, образована в результате его пересечения с некоторой плоскостью (рисунок ниже). Рассмотрим алгоритм построения линии n на развертке.
Задача на определение диаметра через известную площадь конуса и его образующую
Для получения ответа на поставленный вопрос используем описанную в статье методику. Сначала выпишем соответствующее уравнение:
r 2 + 14*r — 150/3,14 = 0
При получении последнего равенства мы разделили левую и правую его части на число Пи. Рассчитываем дискриминант D. Имеем:
D = 14 2 — 4*1*(-150/3,14) = 387,0828
Полученный дискриминант приведен с точностью до 0,0001. Формула для корней уравнения r имеет следующий вид:
Очевидно, что один из корней будет отрицательным. Его не будем вычислять. Определим лишь искомый положительный радиус фигуры:
r = (-14+√387,0828)/2 = 2,837 см
Чтобы найти диаметр конуса, остается умножить это значение на два и записать ответ: d = 5,674 см.
В конце отметим, что, зная два любых параметра круглого конуса прямого, можно определить любую его характеристику, включая объем и площадь поверхности.
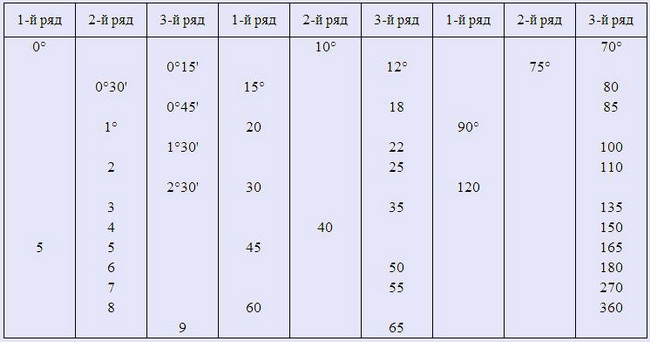
Нормальные углы и конусы инструментов
НОРМАЛЬНЫЕ УГЛЫ ( ГОСТ 8908-81 )
  Таблица не распространяется на угловые размеры конусов. При выборе углов 1-й ряд следует предпочитать 2-му, а 2-й — 3-му.
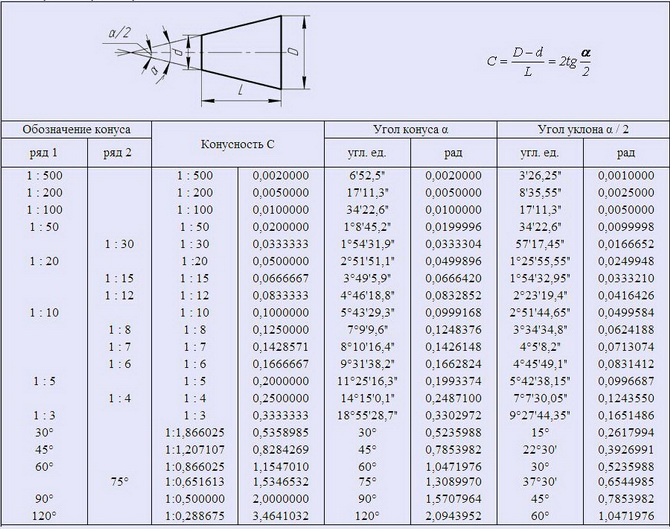
НОРМАЛЬНЫЕ КОНУСНОСТИ и УГЛЫ КОНУСОВ ( ГОСТ 8593-81 )
  Стандарт распространяется на конусности и углы конусов гладких конических элементов деталей.
  Примечание. Значения конусности или угла конуса, указанные в графе «Обозначение конуса», приняты за исходные при расчете других значений, приведенных в таблице. При выборе конусностей или углов конусов ряд 1 следует предпочитать ряду 2.
КОНУСЫ ИНСТРУМЕНТОВ УКОРОЧЕННЫЕ ( ГОСТ 9953-82 )
  Стандарт распространяется на укороченные инструментальные конусы Морзе.
  *z — наибольшее допускаемое отклонение положения основной плоскости, в которой находится диаметр D от теоретическогот положения.   ** размеры для справок.
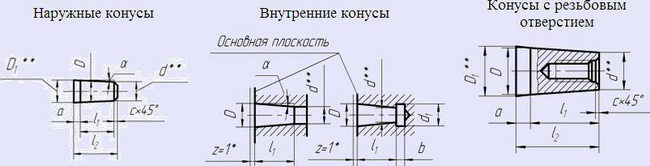
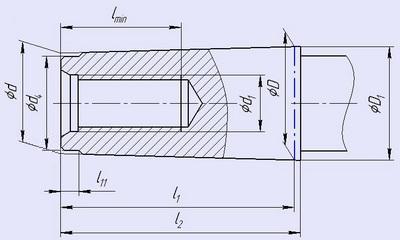
КОНУСНОСТЬ НАРУЖНЫХ И ВНУТРЕННИХ КОНУСОВ И КОНУСОВ С РЕЗЬБОВЫМ ОТВЕРСТИЕМ
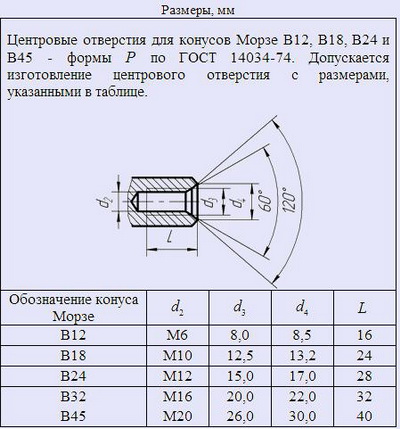
РЕКОМЕНДУЕМЫЕ РАЗМЕРЫ ЦЕНТРОВОГО ОТВЕРСТИЯ УКОРОЧЕННОГО КОНУСА
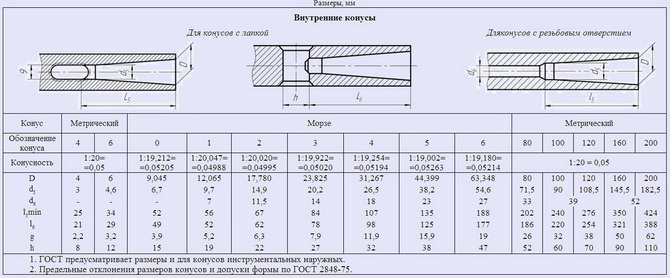
КОНУСЫ ИНСТРУМЕНТАЛЬНЫЕ МОРЗЕ И МЕТРИЧЕСКИЕ НАРУЖНЫЕ( ГОСТ 25557-2006 )
  Профиль резьбового отверстия соответствует отверстию центровому форма Р по ГОСТ ГОСТ 14034-74.
  В ГОСТ 25557-2006 все размеры центрового отверстия приводятся в общей таблице. Стандарт также определяет размеры пазов канавок и отвестий, необходимых для конструирования конусов, в случае подачи смазочно-охлаждающей жидкости (СОЖ) через инструмент.
  В зависимости от конструкции инструментальный хвостовик может иметь соответствующее обозначение:
BI — внутренний конус с пазом; BE — наружный конус с лапкой; AI — внутренний конус с отверстием по оси; АЕ — наружный конус с резьбовым отверстием по оси; BIK — внутренний конус с пазом и отверстием для подачи СОЖ; ВЕК — наружный конус с лапкой и отверстием для подачи СОЖ; AIK — внутренний конус с отверстием по оси и отверстием для подачи СОЖ; АЕК — наружный конус с резьбовым отверстием по оси и отверстием для подачи СОЖ.
КОНУСЫ ИНСТРУМЕНТАЛЬНЫЕ МОРЗЕ И МЕТРИЧЕСКИЕ ВНУТРЕННИЕ( ГОСТ 25557-2006 )
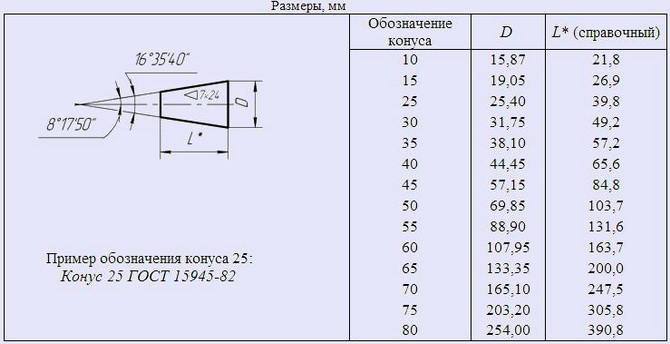
КОНУСЫ ВНУТРЕННИЕ И НАРУЖНЫЕ КОНУСНОСТЬЮ 7 : 24 ( ГОСТ 15945-82 )
  Допуски конусов внутренних и наружных конусностью 7:24 по ГОСТ 19860-93.
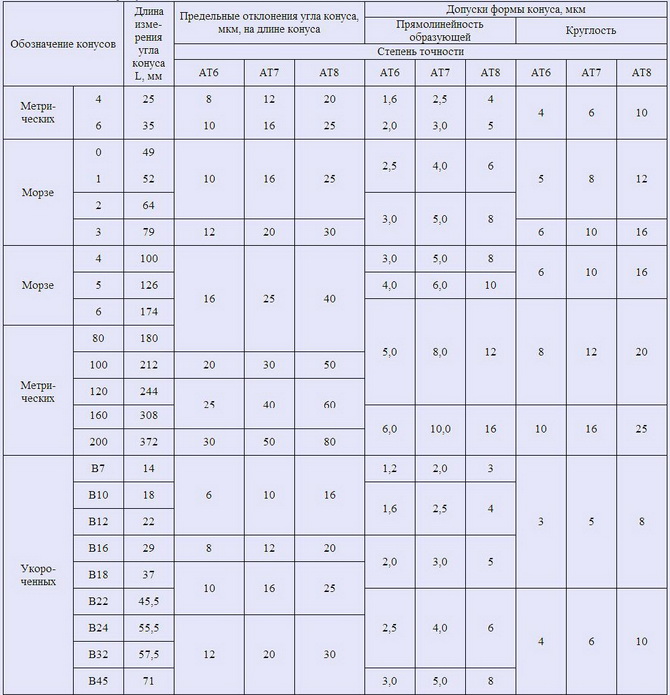
КОНУСЫ ИНСТРУМЕНТОВ Предельные отклонения угла конуса и допуски формы конусов ( ГОСТ 2848-75 )
  Степень точности инструментальных конусов обозначается допуском угла конуса заданной степени точности по ГОСТ 8908-81 и определяется предельными отклонениями угла конуса и допусками формы поверхности конуса, числовые значения которых указаны ниже.
  Примечания:   1. Отклонения угла конуса от номинального размера располагав в «плюс» — для наружных конусов, в «минус» — для внутренних.   2. ГОСТ 2848-75 для наружных конусов предусматривает также степени точности АТ4 и АТ5. Допуски по ГОСТ 2848-75 распространяются на конусы инструментов по ГОСТ 25557-2006 и ГОСТ 9953-82.
  Пример обозначения конуса Морзе 3, степени точности АТ8:
Морзе 3 АТ8 ГОСТ 25557-2006
  То же метрического конуса 160, степени точности АТ7:
Метр. 160 АТ7 ГОСТ 25557-2006
  То же укороченного конуса В18, степени точности АТ6:
Морзе В18 АТ6 ГОСТ 9953-82
ГОСТ 2848-75 — Конусы инструментов. Допуски. Методы и средства контроля ГОСТ 7343-72 — Конусы инструментов с конусностью 1:10 и 1:7. Размеры ГОСТ 10079-71 — Развертки конические с коническим хвостовиком под конусы Морзе. Конструкция и размеры ГОСТ 22774-77 — Конусы и трубки шлифовальные. Типы и размеры ГОСТ 25548-82 — Основные нормы взаимозаменяемости. Конусы и конические соединения. Термины и определения
Как изготовить конус из листового металла. Как сделать развертку – выкройку для конуса или усеченного конуса заданных размеров
Калькуляторы расчета размеров развертки конуса
Иногда в ходе выполнения тех или иных хозяйственных работ мастер встаёт перед проблемой изготовления конуса – полного или усеченного. Это могут быть операции, скажем, с тонким листовым металлом, эластичным пластиком, обычной тканью или даже бумагой или картоном. А задачи встречаются самый разные – изготовление кожухов, переходников с одного диаметра на другой, козырьков или дефлекторов для дымохода или вентиляции, воронок для водостоков, самодельного абажура. А может быть даже просто маскарадного костюма для ребенка или поделок, заданных учителем труда на дом.

Калькуляторы расчета размеров развертки конуса
Чтобы из плоского материала свернуть объёмную фигуру с заданными параметрами, необходимо вычертить развертку. А для этого требуется рассчитать математически и перенести графически необходимые точные размеры этой плоской фигуры. Как это делается – рассмотрим в настоящей публикации. Помогут нам в этом вопросе калькуляторы расчета размеров развертки конуса.










Технология гибки листового металла своими руками
В процессе строительства дома или дачи зачастую появляется необходимость в оборудовании водостоков, канализации, каркасов из металла.
При изготовлении подобных изделий необходимо придать плоской заготовке необходимую пространственную форму. Советы опытных мастеров, как загнуть лист металла в домашних условиях, позволят изготавливать конструкции хорошего качества, которые прослужат долгое время.
Технология гибки – основные сведения
Сгибание металла выполняют без сварочных швов, что позволяет избежать коррозии в дальнейшем и получить изделие повышенной прочности. Деформация не требует значительных усилий и выполняется, как правило, в холодном состоянии.
Исключение составляют твердые материалы, вроде дюрали или углеродистых сталей. Технология гибки листового металла разрабатывается соответственно поставленным задачам в таких вариантах, как:
Калькуляторы расчета размеров развертки конуса
Несколько слов о рассчитываемых параметрах
Понять принцип расчета будет несложно, разобравшись со следующей схемой:

Усеченный конус с определяющими размерами и его развёртка. Показан усеченный конус, но с полным — принцип не меняется, а расчеты и построение становятся даже проще.
Итак, сам конус определяется радиусами оснований (нижней и верхней окружности) R1 и R2, и высотой Н. Понятно, что если конус не усеченный, то R2 просто равно нулю.
Буквой L обозначена длина боковой стороны (образующей) конуса. Она в некоторых случаях уже известна – например, требуется сделать конус по образцу или выкроить материал для обтяжки уже имеющегося каркаса. Но если она неизвестна – не беда, ее несложно рассчитать.
Справа показана развёртка. Она для усеченного конуса ограничена сектором кольца, образованного двумя дугами, внешней и внутренней, с радиусами Rb и Rs. Для полного конуса Rs также будет равен нулю. Хорошо видно, что Rb = Rs + L
Угловую длину сектора определяет центральный угол f, который в любом случае предстоит рассчитать.
Все расчеты займут буквально минуту, если воспользоваться предлагаемыми калькуляторами:
Шаг 1 – определение длины образующей L
(Если она уже известна – шаг пропускается)
Шаг 2 – определение радиусов внутренней и внешней дуги развертки
Радиусы рассчитываются поочередно – с выбором в соответствующем поле калькулятора.
Гибка металла на вальцах
07 Дек 2013 Рубрика: Механика |
За последнее время ко мне было несколько обращений от читателей блога за помощью в решении одной и той же задачи: как при работе на трехвалковых листогибочных вальцах и профилегибах определить окончательное местоположение среднего ролика (валка)…
…относительно положения крайних роликов (валков), которое обеспечит гибку (вальцовку) заготовки с определенным заданным необходимым радиусом? Ответ на этот вопрос позволит повысить производительность труда при гибке металла за счет уменьшения количества прогонов заготовки до момента получения годной детали.
В этой статье вы найдете теоретическое
решение поставленной задачи. Сразу оговорюсь – на практике я этот расчет не применял и, соответственно, не проверял результативность предлагаемого метода. Однако я уверен, что в определенных случаях гибка металла может быть выполнена гораздо быстрее при использовании этой методики, чем обычно.
Чаще всего в обычной практике окончательное местоположение подвижного центрального ролика (валка) и количество проходов до получения годной детали определяется «методом тыка». После длительной (или не очень) отработки технологического процесса на пробной детали определяют координату положения центрального ролика (валка), которую и используют при дальнейших перенастройках вальцев, изготавливая партию этих деталей.
Метод удобен, прост и хорош при значительном количестве одинаковых деталей – то есть при серийном производстве. При единичном или «очень мелкосерийном» производстве, когда необходимо гнуть разные профили или листы разной толщины разными радиусами, потери времени на настройку «методом тыка» становятся катастрофически огромными. Особенно эти потери заметны при гибке длинных (8…11м) заготовок! Пока сделаешь проход…, пока проведешь замеры…, пока перестроишь положение ролика (валка)… — и все сначала! И так десяток раз.
Расчет в Excel местоположения подвижного среднего ролика
Запускаем программу MS Excel или программу OOo Calc, и начинаем работу!
С общими правилами форматирования электронных таблиц, которые применяются в статьях блога, можно ознакомитьсяздесь.
Прежде всего, хочу заметить, что листогибочные вальцы и профилегибы разных моделей могут иметь подвижные крайние ролики (валки), а могут — подвижный средний ролик (валок). Однако для нашей задачи это не имеет принципиального значения.
На рисунке, расположенном ниже изображена расчетная схема к задаче.
Вальцуемая деталь в начале процесса лежит на двух крайних роликах (валках), имеющих диаметр D
. Средний ролик (валок) диаметром
d
подводится
до касания с верхом заготовки
.
Далее средний ролик (валок) опускается вниз на расстояние равное расчетному размеру H
, включается привод вращения роликов, заготовка прокатывается, производится гибка металла, и на выходе получается деталь с заданным радиусом изгиба
R
! Осталось дело за малым – правильно, быстро и точно научиться рассчитывать размер
H
. Этим и займемся.
Исходные данные:
1. Диаметр подвижного верхнего ролика (валка) /справочно/ d
в ячейку D3: 120
2. Диаметр опорных с приводом вращения крайних роликов (валков) D
в ячейку D4: 150
3. Расстояние между осями опорных крайних роликов (валков) A
в ячейку D5: 500
4. Высоту сечения детали h
в ячейку D6: 36
5. Внутренний радиус изгиба детали по чертежу R
в ячейку D7: 600
Расчеты и действия:
6. Вычисляем расчетную вертикальную подачу верхнего ролика (валка)Hрасч
в мм
без учета пружинения
в ячейке D9: =D4/2+D6+D7- ((D4/2+D6+D7)2- (D5/2)2)(½)=45,4
7. Настраиваем вальцы на этот размер Hрасч
и делаем первый прогон заготовки. Измеряем или высчитываем по хорде и высоте сегмента получившийся в результате внутренний радиус, который обозначим
R
и записываем полученное значение в мм
в ячейку D10: 655
8. Вычисляем какой должна была бы быть расчетная теоретическая вертикальная подача верхнего ролика (валка)H0расч
в мм для изготовления детали с радиусом
R
без учета пружинения
в ячейке D11: =D4/2+D6+D10- ((D4/2+D6+D10)2- (D5/2)2)(½)=41,9
H0расч=D/2+h+
R0— ((D/2+h+R0)2- (A/2)2)(½)
9. Но деталь с внутренним радиусом изгиба
Rполучилась при опущенном верхнем валке на размерHрасч, а неH0расч.
Считаем поправку на обратное пружинение
x
в мм
в ячейке D12: =D9-D11=3,5
и
R
имеют близкие размеры, то можно с достаточной степенью точности принять эту же величину поправки
x
для определения окончательного фактического расстояния
H
, на которое необходимо подать вниз верхний ролик (валок) для получения на вальцованной детали внутреннего радиуса
R
.
Вычисляем окончательную расчетную вертикальную подачу верхнего ролика (валка)H
в мм c учетом пружинения
в ячейке D13: =D9+D12=48,9






Развертка наклонного конуса
Рассмотрим порядок построения развертки боковой поверхности наклонного конуса методом аппроксимации (приближения).
Степень соответствия приближенной развертки действительной зависит от количества граней вписанной пирамиды. Число граней выбирают, исходя из удобства чтения чертежа, требований к его точности, наличия характерных точек и линий, которые нужно перенести на развертку.
Перенос линии с поверхности конуса на развертку
Линия n, лежащая на поверхности конуса, образована в результате его пересечения с некоторой плоскостью (рисунок ниже). Рассмотрим алгоритм построения линии n на развертке.
От ровного листа до круглой обечайки:
Вальцы с асимметричным расположением валков (рис.11) производят практически полную гибку обечайки. Наиболее современными являются четырехвалковые машины (рис.12), на которых за один цикл осуществляется вальцовка и подгибка краев. Радиус гибки обечаек проверяют шаблонами. Возможные дефекты вальцовки цилиндрических обечаек приведены на рис.14.
Также способы получения нужной формы бывают разные.
Гибка конических обечаек производится несколькими способами:
1) Установкой под углом среднего валка у симметричных трехвалковых машин и бокового валка у асимметричных трехвалковых и четырехвалковых вальцев (рис.15). 2) Гибкой по средней линии последовательно по различным участкам (рис.16) на вальцах. Сначала осуществляют подгибку кромок, затем гнут середину заготовки на каждом участке с переустановками. Такой способ приводит к повышенному износу оборудования. 3) Гибка обечаек на вальцах со сменными коническими валками. Этот способ оправдан в серийном и массовом производстве. 4) Безвальцевым способом для листа толщиной до 20 мм. На рис. 17 показан метод свертывания. Кромки 3 и 4 заготовки закрепляют в опорах 2 и 5, сводят друг к другу, одновременно поворачивают опоры в разных направлениях. Далее кромки конической обечайки соединяют на прихватках и снимают со станка. 5) Наиболее производительным способом является изготовление конических обечаек в штампах (рис.18). Перед сваркой частей обечаек производят их предварительную фиксацию для исключения деформации элементов и обеспечения сварочных зазоров. Совмещение кромок обычно производится струбцинами и сборочными кольцами для тонкого листа (рис.19). На одну обечайку устанавливается две струбцины по торцам. Цилиндричность обечаек обеспечивается специальными приспособлениями с домкратами, распирающими деталь. При сборке габаритных деталей используются стяжные планки и клиновые соединения (рис.20).
Как сделать дымник – защиту для трубы?
Чтобы в дымовую трубу не попадали осадки, чтобы она не разрушалась льдом, её нужно защитить дымником. Мастера-жестянщики могут изготовить дымник на трубу самых причудливых форм, иногда на дымник устанавливают флюгер, указывающий направление ветра. Но сделать дымник простой конструкции на дымоходную трубу из металла или кирпича можно и своими руками.
С давних времен дымники защищали дымоходы домов, не потеряли они своей актуальности и в наши дни. Если дровяные печи в домах сегодня редкость, то почти в каждом загородном доме есть камин, вытяжную трубу которого необходимо оградить от попадания в неё атмосферных осадков, птиц, осенней листвы и других посторонних предметов.
Нуждаются в такой же защите и все остальные трубы, выходящие на крышу: вентиляционные и дымовые трубы газовых отопительных приборов. Кроме защитной и декоративной функции, дымники способны выполнять ещё одну: они улучшают циркуляцию горячего воздуха в каминах и печах. Разберемся, как сделать дымник на трубу своими руками.
Виды дымников
Дымники могут отличаться друг от друга формой крыши, материалом изготовления, наличием дополнительных конструктивных элементов. Поэтому, прежде чем приступить к выполнению работ своими руками, стоит познакомиться с их разновидностями.
Формы крыши дымников
Достаточно внимательно посмотреть на крыши домов в какой-нибудь деревне или загородном поселке, чтобы убедиться в том, что человеческая фантазия неистощима на разные выдумки. Дымовые трубы украшают дымники самых разных форм, а некоторые умельцы приспосабливают вместо них дырявые чугунки, чайники, ведра и даже молочные фляги.
Если же вы хотите сделать настоящий красивый дымник своими руками, вам будет интересно узнать о том, какую форму ему можно придать. Различают следующие формы крыш дымников:
На фотографиях ниже вы можете увидеть некоторые из перечисленных вариантов.
Дымник с вальмовой крышей
Дымник с четырехщипцовой крышей
Материалами для изготовления дымников чаще всего служат оцинкованная или нержавеющая сталь, листовая медь. Они могут иметь полимерное покрытие различных оттенков для защиты от коррозии.
Для справки: если ваша печь или камин топятся дровами, не имеет смысла устанавливать на трубе окрашенный дымник. Он быстро потеряет цвет, покрывшись копотью и сажей.
Конструктивные особенности
Независимо от формы, дымники часто оснащаются дополнительными конструктивными элементами.
Как самостоятельно устроить дымник?
Рассмотрим, как сделать дымник на трубу своими руками на самых простых примерах. Такие дымники сможет сделать своими руками даже человек, никогда не имевший дела с изготовлением изделий из металла.
Сводчатый дымник
Для изготовления такого дымника своими руками вам потребуется всего пять простых деталей: согнутый дугой прямоугольный лист металла и четыре стойки.
Схема изготовления дымника со сводчатой крышей
Как сделать ровный конус из бумаги. Как сделать развертку – выкройку для конуса или усеченного конуса заданных размеров. Простой расчет развертки
Как сделать развертку – выкройку для конуса или усеченного конуса заданных размеров. Простой расчет развертки.
Иногда возникает задача – изготовить защитный зонт для вытяжной или печной трубы, вытяжной дефлектор для вентиляции и т.п. Но прежде чем приступить к изготовлению, надо сделать выкройку (или развертку) для материала. В интернете есть всякие программы для расчета таких разверток. Однако задача настолько просто решается, что вы быстрее рассчитаете ее с помощью калькулятора (в компьютере), чем будете искать, скачивать и разбираться с этими программами.
Начнем с простого варианта — развертка простого конуса. Проще всего объяснить принцип расчета выкройки на примере.
Допустим, нам надо изготовить конус диаметром D см и высотой H сантиметров. Совершенно понятно, что в качестве заготовки будет выступать круг с вырезанным сегментом. Известны два параметра – диаметр и высота. По теореме Пифагора рассчитаем диаметр круга заготовки (не путайте с радиусом готового конуса). Половина диаметра (радиус) и высота образуют прямоугольный треугольник. Поэтому:
Итак, теперь мы знаем радиус заготовки и можем вырезать круг.
Вычислим угол сектора, который надо вырезать из круга. Рассуждаем следующим образом: Диаметр заготовки равен 2R, значит, длина окружности равна Пи*2*R — т.е. 6.28*R. Обозначим ее L. Окружность полная, т.е. 360 градусов. А длина окружности готового конуса равна Пи*D. Обозначим ее Lm. Она, естественно, меньше чем длина окружности заготовки. Нам нужно вырезать сегмент с длиной дуги равной разности этих длин. Применим правило соотношения. Если 360 градусов дают нам полную окружность заготовки, то искомый угол должен дать длину окружности готового конуса.
Из формулы соотношения получаем размер угла X. А вырезаемый сектор находим путем вычитания 360 – Х.
Из круглой заготовки с радиусом R надо вырезать сектор с углом (360-Х). Не забудьте оставить небольшую полоску материала для нахлеста (если крепление конуса будет внахлест). После соединения сторон вырезанного сектора получим конус заданного размера.
Например: Нам нужен конус для зонта вытяжной трубы высотой (Н) 100 мм и диаметром (D) 250 мм. По формуле Пифагора получаем радиус заготовки – 160 мм. А длина окружности заготовки соответственно 160 x 6,28 = 1005 мм. В тоже время длина окружности нужного нам конуса — 250 x 3,14 = 785 мм.
Тогда получаем, что соотношение углов будет такое: 785 / 1005 x 360 = 281 градус. Соответственно вырезать надо сектор 360 – 281 = 79 градусов.
Расчет заготовки выкройки для усеченного конуса.
Такая деталь бывает нужна при изготовлении переходников с одного диаметра на другой или для дефлекторов Вольперта-Григоровича или Ханженкова. Их применяют для улучшения тяги в печной трубе или трубе вентиляции.
Задача немного осложняется тем, что нам неизвестна высота всего конуса, а только его усеченной части. Вообще же исходных цифр тут три: высота усеченного конуса Н, диаметр нижнего отверстия (основания) D, и диаметр верхнего отверстия Dm (в месте сечения полного конуса). Но мы прибегнем к тем же простым математическим построениям на основе теоремы Пифагора и подобия.
В самом деле, очевидно, что величина (D-Dm)/2 (половина разности диаметров) будет относиться с высотой усеченного конуса Н так же, как и радиус основания к высоте всего конуса, как если бы он не был усечен. Находим полную высоту (P) из этого соотношения.
Отсюда Р = D x H / (D-Dm).
Теперь зная общую высоту конуса, мы можем свести решение задачи к предыдущей. Рассчитать развертку заготовки как бы для полного конуса, а затем «вычесть» из нее развертку его верхней, ненужной нам части. А можем рассчитать непосредственно радиусы заготовки.
Получим по теореме Пифагора больший радиус заготовки — Rz. Это квадратный корень из суммы квадратов высоты P и D/2.
Меньший радиус Rm – это квадратный корень из суммы квадратов (P-H) и Dm/2.
Теперь осталось рассчитать угол сектора, который надо вырезать.
Длина окружности нашей заготовки равна 2 х Пи х Rz, или 6,28 х Rz. А длина окружности основания конуса – Пи х D, или 3,14 х D. Соотношение их длин и дадут соотношение углов секторов, если принять, что полный угол в заготовке – 360 градусов.
Т.е. Х / 360 = 3,14 x D / 6.28 x Rz
Отсюда Х = 180 x D / Rz (Это угол, который надо оставить, что бы получить длину окружности основания). А вырезать надо соответственно 360 – Х.
Например: Нам надо изготовить усеченный конус высотой 250 мм, диаметр основание 300 мм, диаметр верхнего отверстия 200 мм.
Находим высоту полного конуса Р: 300 х 250 / (300 – 200) = 600 мм
По т. Пифагора находим внешний радиус заготовки Rz: Корень квадратный из (300/2)^2 + 6002 = 618,5 мм
По той же теореме находим меньший радиус Rm: Корень квадратный из (600 – 250)^2 + (200/2)^2 = 364 мм.
Определяем угол сектора нашей заготовки: 180 х 300 / 618,5 = 87.3 градуса.
На материале чертим дугу с радиусом 618,5 мм, затем из того же центра – дугу радиусом 364 мм. Угол дуги может имеет примерно 90-100 градусов раскрытия. Проводим радиусы с углом раскрытия 87.3 градуса. Наша заготовка готова. Не забудьте дать припуск на стыковку краев, если они соединяются внахлест.
Константин Тимошенко © 31.07.2014 г.
Как вы решили этот пример? 300 х 250 / (300 – 200) = 600 мм
Калькуляторы расчета размеров развертки конуса
Иногда в ходе выполнения тех или иных хозяйственных работ мастер встаёт перед проблемой изготовления конуса – полного или усеченного. Это могут быть операции, скажем, с тонким листовым металлом, эластичным пластиком, обычной тканью или даже бумагой или картоном. А задачи встречаются самый разные – изготовление кожухов, переходников с одного диаметра на другой, козырьков или дефлекторов для дымохода или вентиляции, воронок для водостоков, самодельного абажура. А может быть даже просто маскарадного костюма для ребенка или поделок, заданных учителем труда на дом.

Чтобы из плоского материала свернуть объёмную фигуру с заданными параметрами, необходимо вычертить развертку. А для этого требуется рассчитать математически и перенести графически необходимые точные размеры этой плоской фигуры. Как это делается – рассмотрим в настоящей публикации. Помогут нам в этом вопросе калькуляторы расчета размеров развертки конуса.
Калькуляторы расчета размеров развертки конуса
Несколько слов о рассчитываемых параметрах
Понять принцип расчета будет несложно, разобравшись со следующей схемой:

Итак, сам конус определяется радиусами оснований (нижней и верхней окружности) R1 и R2, и высотой Н. Понятно, что если конус не усеченный, то R2 просто равно нулю.
Буквой L обозначена длина боковой стороны (образующей) конуса. Она в некоторых случаях уже известна – например, требуется сделать конус по образцу или выкроить материал для обтяжки уже имеющегося каркаса. Но если она неизвестна – не беда, ее несложно рассчитать.
Справа показана развёртка. Она для усеченного конуса ограничена сектором кольца, образованного двумя дугами, внешней и внутренней, с радиусами Rb и Rs. Для полного конуса Rs также будет равен нулю. Хорошо видно, что Rb = Rs + L
Угловую длину сектора определяет центральный угол f, который в любом случае предстоит рассчитать.
Все расчеты займут буквально минуту, если воспользоваться предлагаемыми калькуляторами:
Шаг 1 – определение длины образующей L
(Если она уже известна – шаг пропускается)
Шаг 2 – определение радиусов внутренней и внешней дуги развертки
Радиусы рассчитываются поочередно – с выбором в соответствующем поле калькулятора.
Построение развертки конуса
Развертка поверхности конуса — это плоская фигура, полученная путем совмещения боковой поверхности и основания конуса с некоторой плоскостью.
Варианты построения развертки:
Развертка прямого кругового конуса
Развертка боковой поверхности прямого кругового конуса представляет собой круговой сектор, радиус которого равен длине образующей конической поверхности l, а центральный угол φ определяется по формуле φ=360*R/l, где R – радиус окружности основания конуса.
В ряде задач начертательной геометрии предпочтительным решением является аппроксимация (замена) конуса вписанной в него пирамидой и построение приближенной развертки, на которую удобно наносить линии, лежащие на конической поверхности.
На рисунке ниже в прямой круговой конус вписана правильная шестиугольная пирамида SABCDEF, и приближенная развертка его боковой поверхности состоит из шести равнобедренных треугольников – граней пирамиды.
Точки A, B, C, D, E и F, лежащие в основании конуса, соединяем плавной кривой – дугой окружности, радиус которой равен l.
Развертка наклонного конуса
Рассмотрим порядок построения развертки боковой поверхности наклонного конуса методом аппроксимации (приближения).
Степень соответствия приближенной развертки действительной зависит от количества граней вписанной пирамиды. Число граней выбирают, исходя из удобства чтения чертежа, требований к его точности, наличия характерных точек и линий, которые нужно перенести на развертку.
Перенос линии с поверхности конуса на развертку
Линия n, лежащая на поверхности конуса, образована в результате его пересечения с некоторой плоскостью (рисунок ниже). Рассмотрим алгоритм построения линии n на развертке.
Развертка усеченного конуса
Описываемый ниже способ построения развертки прямого кругового усеченного конуса основан на принципе подобия.
Источники информации:
- http://stroyday.ru/kalkulyatory/obshhestroitelnye-voprosy/kalkulyatory-rascheta-razmerov-razvertki-konusa.html
- http://1ku.ru/obrazovanie/44223-chto-takoe-razvertka-konusa-i-kak-ee-postroit-formuly-i-primer-reshenija-zadachi/
- http://gostevushka.ru/konus-iz-bumagi-kak-sdelat
- http://lformat.ru/weblog/cone-paper-cup/
- http://mo-dmitr.ru/pro-tehnologii/chertezh-konusa.html
- http://saddrakona.ru/podelki/kak-postroit-konus.html
- http://svetluxe.ru/razvertka-konusa/
- http://nwjs.ru/obrabotka/konus-iz-metalla-svoimi-rukami.html
- http://igrad.su/vse-zapisi/kak-sdelat-rovnyj-konus-iz-bumagi-kak-sdelat-razvertku-vykrojku-dlya-konusa-ili-usechennogo-konusa-zadannyh-razmerov-prostoj-raschet-razvertki.html




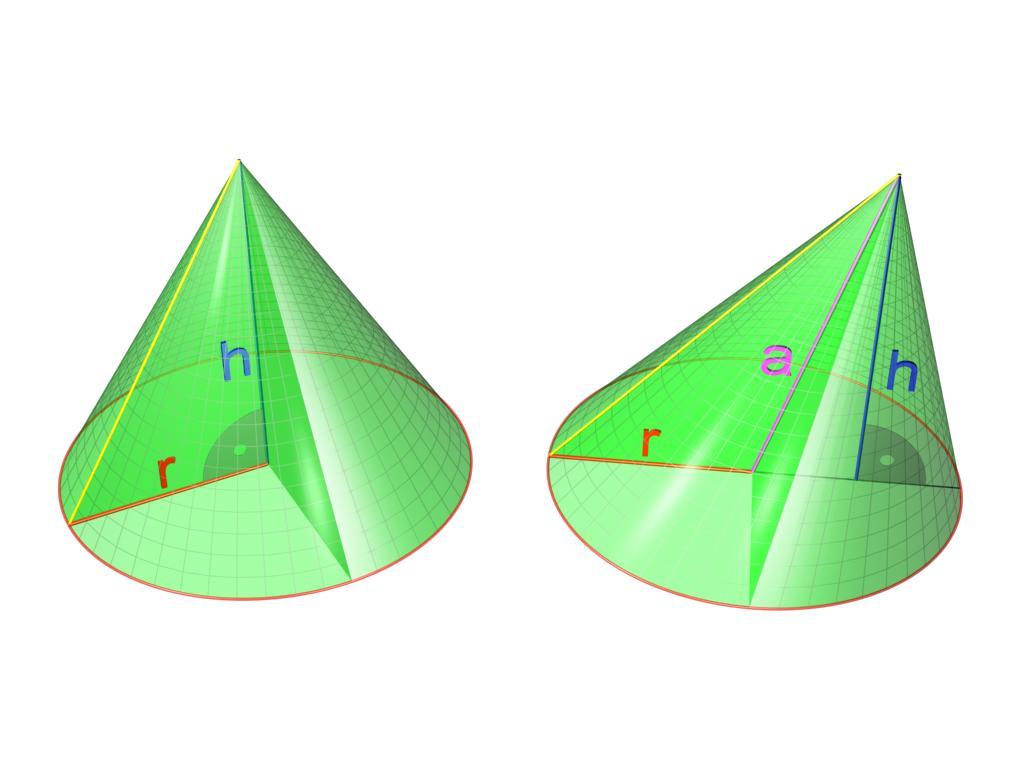
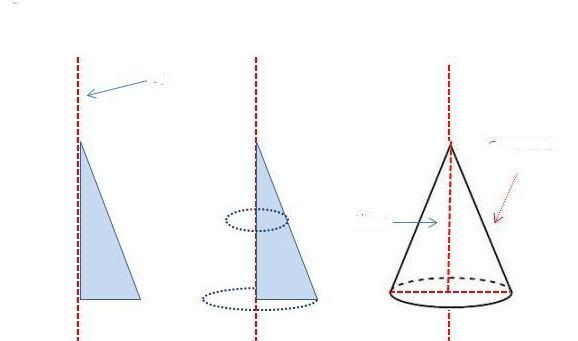
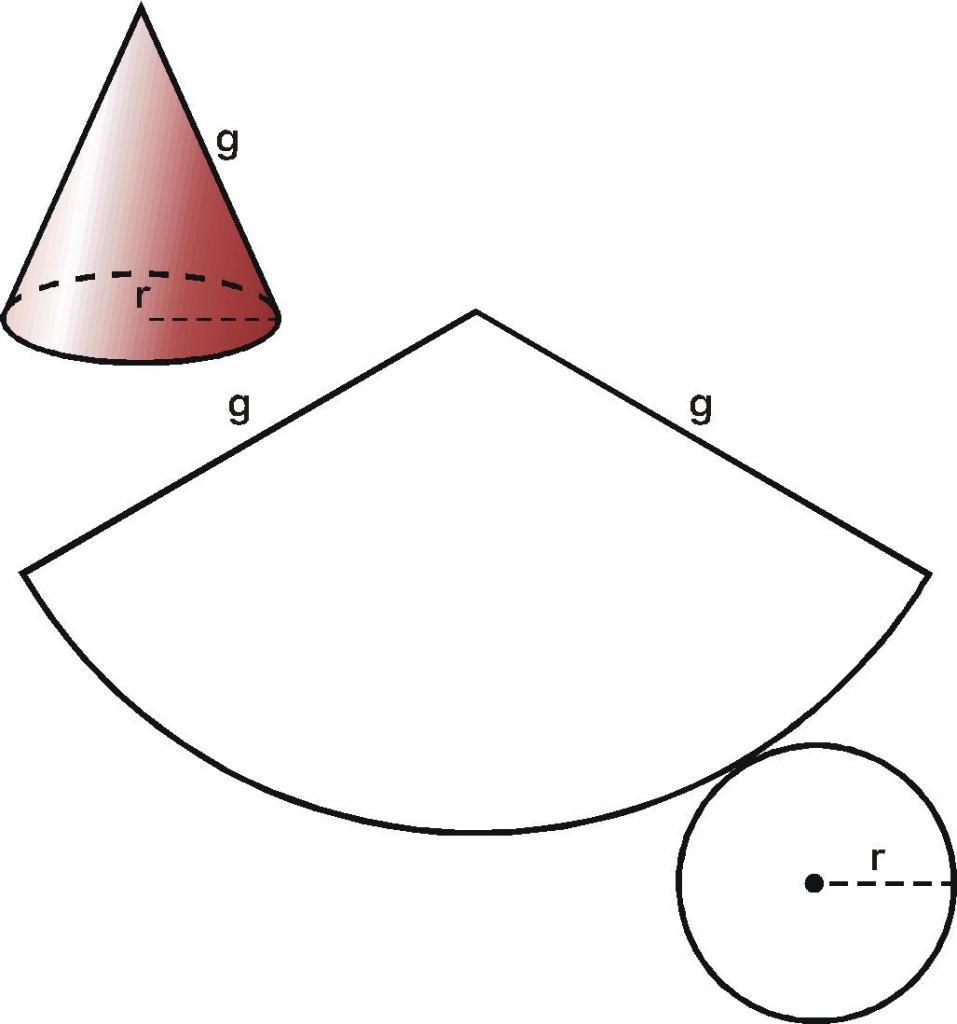
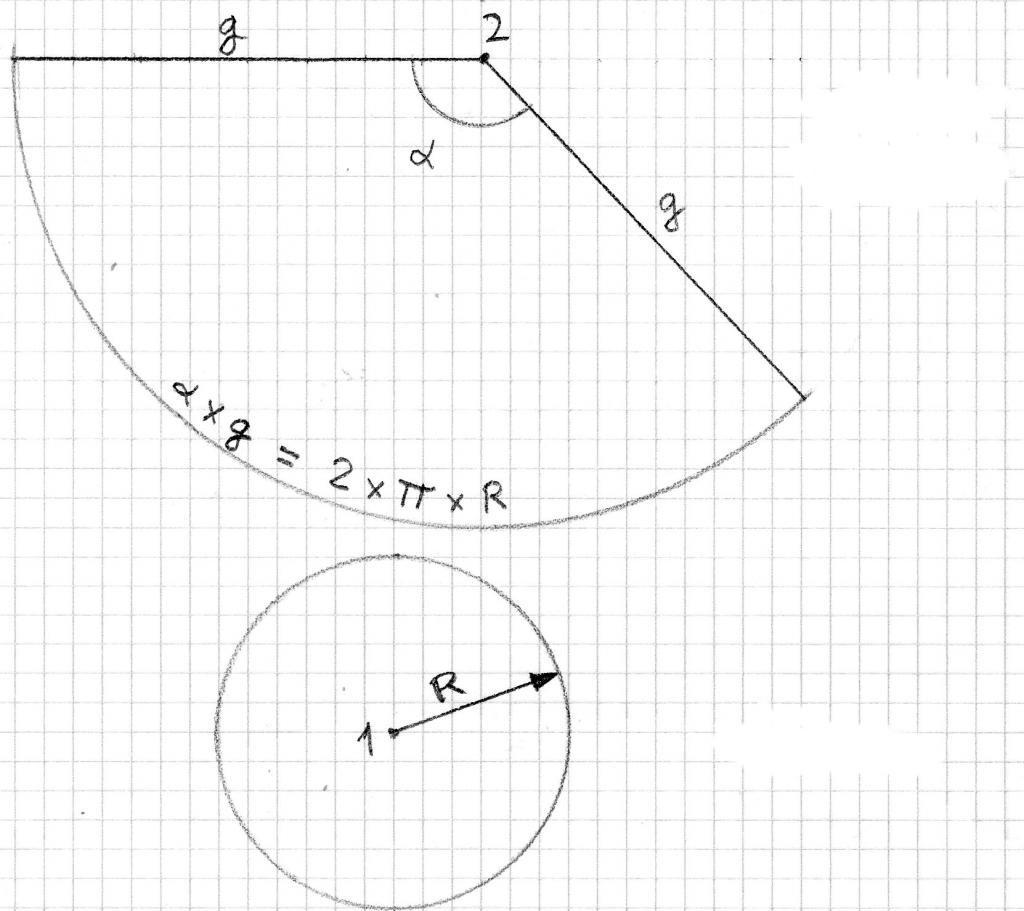
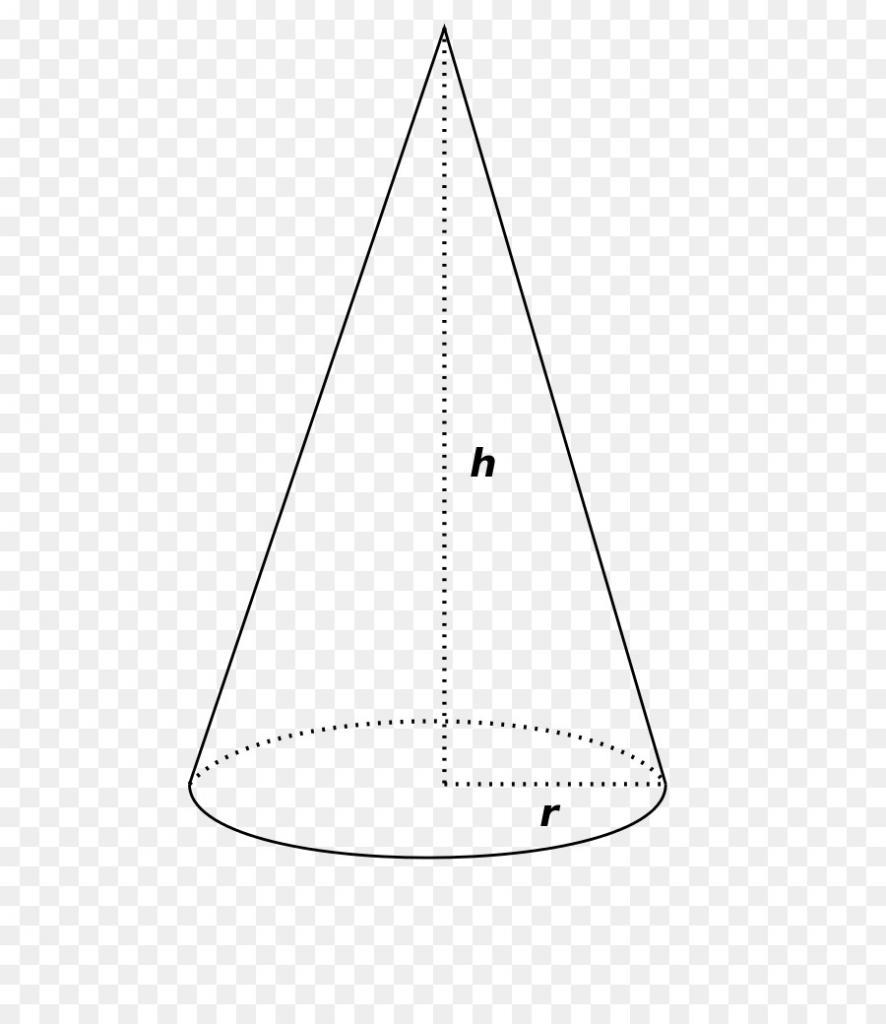


 Развертка усеченного конуса
Развертка усеченного конуса