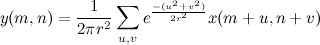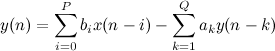Как сделать размытие по гауссу в фотошопе

Быстрое размытие по Гауссу

Фильтр размытия по гауссу (широко известный “gaussian blur” в фотошопе) достаточно часто применяется сам по себе или как часть других алгоритмов обработки изображений. Далее будет описан метод, позволяющий получать размытие со скоростью, не зависящей от радиуса размытия, используя фильтры с бесконечной импульсной характеристикой.

Описание метода есть на английском. Но на русском информации нет. Кроме того, мною были внесены некоторые изменения.

Итак, пусть исходное изображение будет задано яркостью x(m,n). Гаусово размытие с радиусом r считается по формуле

Пределы суммирования по u и v можно выбирать как плюс минус несколько сигм, т.е. радиусов r, что даёт сложность алгоритма порядка O(r 2 ) операций на пиксель. Для больших r и многомегапиксельных изображений не слишком здорово, правда?

Первое ускорение даёт свойство сепарабельности гауссова размытия. То есть, можно провести фильтрацию по оси x для каждой строки, полученное изображение отфильтровать по y по каждому столбцу и получить тот же результат со сложностью O(r) операций на пиксель. Уже лучше. Это свойство мы тоже будем использовать, поэтому дальше все рассуждения будут для одномерного случая, где нужно получить y(n) имея x(n).

В этом нам помогут фильтры с бесконечной импульсной характеристикой. Идея фильтра такова: значения y(n) рекуррентно рассчитываются по формуле:

Т.е. дальше нужно просто подобрать три похожие функции, каждая из которых стремится в пределе в константе. Я искал функции в виде отношения

и подобрал коэффициенты самым простым образом — просто использовав Wolfram Mathematica. Кстати, если внимательно изучать графики данных из таблиц, видно что функция имеет несколько пилообразную структуру. Поэтому при аппроксимации мы немного потеряем в точности, но по факту совсем чуть чуть — значения из таблицы дадут ошибку на 10 процентов меньшую, чем полученные полиномами.

Ну вот. Для тех, кто уже запутался что и от чего нужно считать, приведу финальный код функции на С для расчёта коэффициентов:

Всё! Теперь, нужно написать сам код. Расчёт, конечно, нужно производить во float, но современные компьютеры считают на числа с плавающей запятой (особенно с sse) довольно быстро. Программисты из Интел, кстати, озаботились оптимизацией Gauss-IIR фильтров под векторные инструкции процессора уже написали целую статью. Правда, там считают немножко другим методом, но основные способы оптимизации описаны хорошо.

В конце можно дать пример того, что получилось:

Картинка практически не отличается от «честной». Впрочем, если открыть её в фотошопе и поизучать внимательно, разницу найти можно.