Как сделать многогранник из бумаги своими руками
Как сделать многогранник из бумаги своими руками
Развёртки многогранников. Методический материал для конструирования пространственных фигур.
Столичный центр образовательных технологий г. Москва
Получите квалификацию учитель математики за 2 месяца
от 3 170 руб. 1900 руб.
Количество часов 300 ч. / 600 ч.
Успеть записаться со скидкой
Форма обучения дистанционная
Развёртки геометрических объёмных тел
На плотной бумаге начертите подобную развёртку, вырежьте, аккуратно склейте.




Наклонная треугольная призма












 |


 |







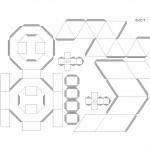
Состоит из 4-х деталей, причем детали под номерами № 3 и 4 — по одной штуке,
а № 1 и 2 — по две штуке
Развертка состоит из прямоугольных треугольников, включает в себя еще и клапаны.
Согнуть развертку по всем необходимым линиям.
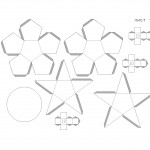
на схеме треугольнички, составляющие звездочку, выделены «крестиками»

Большой звёздчатый додекаэдр:
клеим пирамидки соответствующего размера на додекаэдр
Соединение пяти октаедров
Курс повышения квалификации
Ментальная арифметика: умножение и деление
Курс повышения квалификации
Профилактика синдрома «профессионального выгорания» у педагогов
Курс повышения квалификации
Анализ урока как инструмент развития профессиональных компетенций учителя в соответствии с требованиями ФГОС
«Обзор традиционных и современных методик для формирования навыков арифметических вычислений в уме у младших школьников»
«Кинетический имидж учителя и его невербальное влияние на учеников»
Свидетельство и скидка на обучение каждому участнику
«Начало учебного года современного учителя»
Свидетельство и скидка на обучение каждому участнику
Дистанционные курсы для педагогов
311 лекций для учителей,
воспитателей и психологов
Получите свидетельство
о просмотре прямо сейчас!
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 885 608 материалов в базе
«Нейроигры для детей от 1 до 7»
Свидетельство и скидка на обучение каждому участнику
«Управление знаниями и интеллектуальным капиталом образовательного учреждения»
Свидетельство и скидка на обучение каждому участнику
Ищем педагогов в команду «Инфоурок»
Другие материалы
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Настоящий материал опубликован пользователем Ясинко Юлия Николаевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Дистанционные курсы
для педагогов
663 курса от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
«Методическое сопровождение образовательного процесса»
«Профилактика насилия в школьной среде»
«Особенности возрастного подхода к социализации воспитанников и обучающихся в условиях современной информационной среды»
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Геометрические фигуры из бумаги: делаем поделку в технике оригами
Оригами открывает невероятные широты для фантазии и творчества. Мастера из бумаги научились делать самые разнообразные поделки. Это разные животные, птицы да даже растения. Но сегодня мы подробно рассмотрим, как делать геометрические фигуры быстро и легко из бумаги.
Такие фигуры помогут развить представление о трёхмерных фигурах, а также общее представления о них. Лучше всего они подойдут тем, у кого возникают сложности с тригонометрией, так как этот раздел геометрии требует очень хорошего визуального представления разных фигур.
Мастерим куб
Итак, для сегодняшнего мастер-класса нам пригодится бумага, схемы, клей, ножницы, линейки и немножечко терпения.
Куб — самая простая фигура для оригами, простой многогранник, в котором каждая грань является квадратом. Схему для создания развертки можно распечатать на принтере, либо начертить самим. Для этого выбрать размеры граней. Ширина листа бумаги должна быть не менее 3 сторон одного квадрата, а длина не более 5 сторон. Начертить в длину листа четыре квадрата, которые станут боковыми сторонами куба. Рисовать строго на одной линии, вплотную. Над и под одним квадратом нарисовать по одному квадрату. Дорисовать полоски для склеивания, благодаря которым грани будут соединяться между собой. Наш куб уже практически готов!
Далее тонким слоем клея равномерно размазать по местам соединения. Склеить эти поверхности и закрепить на некоторое время с помощью скрепки. Клей будет схватываться около 30-40 минут. Таким образом склеить все грани.








Геометрические фигуры из бумаги: делаем поделку в технике оригами в фото
Геометрические фигуры из бумаги должен научиться делать каждый! Ведь никогда не знаешь, какие знания тебе могут пригодиться в жизни. В последнее время техника оригами набирает широкую популярность среди детей и взрослых. Но перед тем как делать разнообразные поделки (животных, птиц, растений, маленьких домиков), нужно начать с простых геометрических фигур. Такие изделия подойдут для школьников для хорошего визуального представления разных фигур.
Куб — самая простая фигура для оригами, простой многогранник, в котором каждая грань является квадратом. Схему для создания развертки можно распечатать на принтере, либо начертить самим. Для этого выбрать размеры граней. Ширина листа бумаги должна быть не менее 3 сторон одного квадрата, а длина не более 5 сторон. Начертить в длину листа четыре квадрата, которые станут боковыми сторонами куба. Рисовать строго на одной линии, вплотную. Над и под одним квадратом нарисовать по одному квадрату. Дорисовать полоски для склеивания, благодаря которым грани будут соединяться между собой. Наш куб уже практически готов!
Далее тонким слоем клея равномерно размазать по местам соединения. Склеить эти поверхности и закрепить на некоторое время с помощью скрепки. Клей будет схватываться около 30-40 минут. Таким образом склеить все грани.
Конус делается немного сложнее. Для начала нарисовать циркулем окружность. Вырезать сектор (часть кружка, ограниченная дугой окружности и двумя радиусами) из этой окружности. Острота конца конуса зависит от вырезанной части большого сектора.
Склеить боковую поверхность конуса. Далее измерить диаметр основания конуса. Циркулем нарисовать окружность на листе бумаги. Затем дорисовать треугольнички для склеивания основы с боковой поверхности. Вырезать. После приклеить основание к боковой поверхности. Поделка готова!
Параллелепипед — сложная фигура многогранник, у которого 6 граней и каждая из них параллелограмм.
Чтобы сделать параллелепипед техникой оригами, нужно начертить основание — параллелограмм любого размера. С каждой его стороны нарисовать боковые стороны — тоже параллелограммы. Далее от любой из боковых сторон дорисовать второе основание. Добавить места для склеивания. Параллелепипед может быть прямоугольным, если все стороны имеют прямые углы. Затем вырезать развертку и склеить. Готово!
Пришло время сделать пирамиду из бумаги. Это многогранник, основание которого — многоугольник, а другие грани — треугольники с общей вершиной.
Для начала нужно выбрать размеры пирамиды и количество граней. Далее нарисовать многогранник — он будет основанием. Смотря на количество граней, это может быть также треугольник, квадрат, пятиугольник.
От одной из сторон нашего многогранника нарисовать треугольник, который будет боковой стороной. Затем нарисовать еще треугольник, чтобы одна его сторона была общей с первым треугольником. Нарисовать их столько, сколько сторон в пирамиде. Далее дорисовать полоски для склеивания в необходимых местах. Вырезать и склеить фигуру. Пирамида готова!
Цилиндр — это геометрическая фигура, ограниченная цилиндрической поверхностью и двумя параллельными плоскостями, которые ее пересекают.
Нарисовать прямоугольник на бумаге, в которой ширина — высота цилиндра, а длина — диаметр. Любители геометрии знают, что отношение длины прямоугольника к диаметру определяется формулой: L=nD, где L — длина прямоугольника, а D — диаметр цилиндра. С помощью этого вычисления узнать длину прямоугольника, которого будем рисовать на бумаге. Дорисовать маленькие треугольнички для склеивания деталей.
Затем нарисовать на бумаге два круга, диаметром как цилиндр. Это будет верхнее и нижнее основания цилиндра. Далее вырезать все детали. Склеить боковую поверхность цилиндра из прямоугольника. Дать детали высохнуть и приклеить к нему нижнее основание. Снова подождать, пока высохнет, и приклеить верхнюю основу. Готово!
Видео по теме статьи










Поделка посложнее
Конус делается немного сложнее. Для начала нарисовать циркулем окружность. Вырезать сектор (часть кружка, ограниченная дугой окружности и двумя радиусами) из этой окружности. Острота конца конуса зависит от вырезанной части большого сектора.
Склеить боковую поверхность конуса. Далее измерить диаметр основания конуса. Циркулем нарисовать окружность на листе бумаги. Затем дорисовать треугольнички для склеивания основы с боковой поверхности. Вырезать. После приклеить основание к боковой поверхности. Поделка готова!
Статья по теме: Варежки с орнаментом спицами: схемы с описанием и видео
Сложный параллелепипед
Параллелепипед — сложная фигура многогранник, у которого 6 граней и каждая из них параллелограмм.
Чтобы сделать параллелепипед техникой оригами, нужно начертить основание — параллелограмм любого размера. С каждой его стороны нарисовать боковые стороны — тоже параллелограммы. Далее от любой из боковых сторон дорисовать второе основание. Добавить места для склеивания. Параллелепипед может быть прямоугольным, если все стороны имеют прямые углы. Затем вырезать развертку и склеить. Готово!
Самый первый многогранник — кубик
Скорее всего, каждый человек, посещавший школу, еще в начальных классах сталкивался на уроках труда с работой, результатом которой должен был стать бумажный кубик. Чаще всего учительница раздавала заготовки — развертки многогранника куба на плотной бумаге со специальными кармашками, предназначенными для склеивания граней модели в единое целое. Такой работой ученики начальной школы могли гордиться, ведь при помощи бумаги, ножниц, клея и своих усилий получалась интересная поделка — трехмерный куб.
Пирамида-оригами
Пришло время сделать пирамиду из бумаги. Это многогранник, основание которого — многоугольник, а другие грани — треугольники с общей вершиной.
Для начала нужно выбрать размеры пирамиды и количество граней. Далее нарисовать многогранник — он будет основанием. Смотря на количество граней, это может быть также треугольник, квадрат, пятиугольник.
От одной из сторон нашего многогранника нарисовать треугольник, который будет боковой стороной. Затем нарисовать еще треугольник, чтобы одна его сторона была общей с первым треугольником. Нарисовать их столько, сколько сторон в пирамиде. Далее дорисовать полоски для склеивания в необходимых местах. Вырезать и склеить фигуру. Пирамида готова!
Интересные факты о додекаэдре
Правильные многогранники с древних времен восхищали человечество и служили прообразом мирового устройства. Как оказалось, подобные представления небезосновательны. В 2003 году, анализируя данные исследовательского аппарата WMAP, запущенного NASA для изучения фоновых космических излучений, учёные выдвинули гипотезу о додекаэдрическом строении Вселенной по принципу сферы Пуанкаре.
Нечто подобное предполагал и живший в V в. до н. э. древнегреческий философ Платон. В своём учении о классических стихиях, он назвал додекаэдр «образцом божественного устройства Космоса». Вообще же все пять известных правильных многогранников до сих пор называют Платоновыми телами, по имени мыслителя, впервые выстроившего с их помощью чёткую картину мироздания.
Пентагон, лежащий в основе додекаэдра, построен на принципах «золотого сечения». Эта пропорция, которую древние греки считали «божественной» часто встречается в природе. Интересно, что соотношения «золотого сечения» присущи лишь додекаэдру и икосаэдру, у трёх других Платоновых тел его нет.
Игрушки древних римлян
На территориях Европы, некогда принадлежавших Римской империи, до сих пор находят загадочные бронзовые фигурки в форме додекаэдра. Предметы пустотелые, с круглыми отверстиями на каждой стороне и шариками, обозначающими вершины. Учёные пока не смогли однозначно определить функцию этих объектов. Первоначально считалось, что это своеобразные игрушки, однако позднее их отнесли к предметам культа, символизирующим устройство Вселенной. Или Земли, согласно теории, последовательно выдвигаемой с XIX века мировыми физиками, в том числе и российскими.
Впервые о том, что наша планета представляет собой кристалл додекаэдрической формы, заговорили французский математик Пуанкаре и геолог-исследователь де Бемон. Они утверждали, что земная кора, словно футбольный мяч, состоит из 12 правильных пятиугольников, в местах соединения которых, располагаются аномальные зоны и планетарные силовые поля.
В 1920-х годах идею французских коллег подхватил русский физик Степан Кислицын. Он пошёл ещё дальше, заявив, что планета не остаётся в стабильном состоянии, она растёт, из додекаэдра постепенно трансформируясь в икосаэдр. Учёный разработал модели подобных изменений, обозначив узлы гигантской кристаллической сетки, где, по его мнению, располагались месторождения полезных ископаемых: угля, нефти, газа и так далее. В 1928 году Кислицын, опираясь на свои исследования, указал на поверхности земного шара 12 алмазоносных центров, из которых 7 к настоящему времени находятся в активной разработке.
Идеи кристаллического строения планеты продолжают развиваться в XXI веке. Согласно последней гипотезе, подобная структура свойственна всем живым организмам, не только космическим телам, но и человеку. Тем интереснее будет собирать додекаэдр-оригами, чувствуя свою сопричастность к великим тайнам Вселенной.
Бумажный цилиндр
Цилиндр — это геометрическая фигура, ограниченная цилиндрической поверхностью и двумя параллельными плоскостями, которые ее пересекают.
Нарисовать прямоугольник на бумаге, в которой ширина — высота цилиндра, а длина — диаметр. Любители геометрии знают, что отношение длины прямоугольника к диаметру определяется формулой: L=nD, где L — длина прямоугольника, а D — диаметр цилиндра. С помощью этого вычисления узнать длину прямоугольника, которого будем рисовать на бумаге. Дорисовать маленькие треугольнички для склеивания деталей.
Затем нарисовать на бумаге два круга, диаметром как цилиндр. Это будет верхнее и нижнее основания цилиндра. Далее вырезать все детали. Склеить боковую поверхность цилиндра из прямоугольника. Дать детали высохнуть и приклеить к нему нижнее основание. Снова подождать, пока высохнет, и приклеить верхнюю основу. Готово!
Статья по теме: Скандинавские узоры для вязания спицами со схемами и фото орнаментов
Как сделать многогранник из бумаги
Для работы понадобится цветной или белый картон, который можно при необходимости раскрасить; линейка и угольники; хороший клей, который не коробит бумагу; ножницы; пинцет. Для изготовления заготовок многогранника удобно пользоваться картонными трафаретами: чертеж заготовки накладывают на плотный картон, шилом или иголкой делают проколы по вершинам детали, после чего по линейке соединяют эти точки.
Тетраэдр
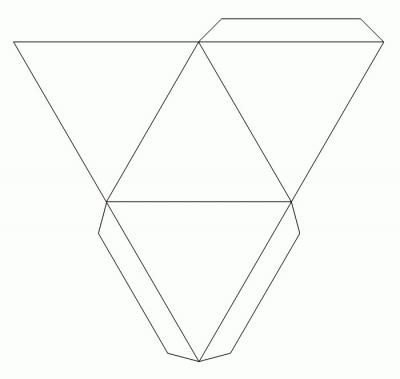
Одним из простейших многогранников, которые проще всего сделать из бумаги (картона), является тетраэдр («Пирамида»). Четыре грани этой фигуры представлены равносторонними треугольниками. Если хочется сделать одноцветный тетраэдр, то можно воспользоваться одной разверткой (см. схему ниже).
Октаэдр
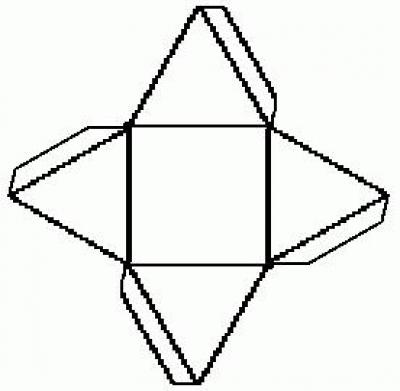
Вторую половину проще клеить таким образом: сначала четыре оставшихся треугольника приклеивают к соответствующим сторонам квадратного основания, затем соединяют соседние грани.
Икосаэдр
На третьем месте по простоте исполнения идет икосаэдр, гранями которого тоже являются равносторонние треугольники. Наиболее эффектно смотрятся разноцветные многогранники, у которых возможно варьирование распределения цветов. Например, можно сделать фигуру, у которой в каждой вершине будут сходиться все используемые цвета, или же у противоположных граней будут одинаковые расцветки, а у вершин будет повторяться один цвет.
Модель собирают из пяти треугольников, соединенных по схеме, указанной на рисунке ниже. В результате получится невысокая пятиугольная пирамида без основания. К сторонам основания приклеивают остальные пять треугольников, руководствуясь любой понравившейся цветовой схемой.
Додекаэдр
И, пожалуй, к несложным, но самым эффектным по своему внешнему виду многогранникам можно отнести додекаэдр. Наиболее красиво выглядят разноцветные додекаэдры: четырех- или шестицветные.
Пример цветовой схемы:
Если вам, уважаемые читатели, интересна тема изготовления многогранников из бумаги, и хотелось бы видеть больше схем, пишите об этом в комментариях, публикации будут продолжены. Впереди нас ждут усеченные, «курносые» и красивейшие звездчатые формы многогранников.
Как сделать из бумаги многогранник. Многогранники из бумаги — схемы

Свое название конструкция получила по количеству входящих в нее граней (традиционно древние греки давали многогранникам имена, отображающие число граней, составляющих структуру фигуры). Таким образом, понятие «додекаэдр» образовано из значений двух слов: «додека» (двенадцать) и «хедра» (грань). Фигура относится к одному из пяти Платоновых тел (наряду с тетраэдром, октаэдром, гексаэдром (кубом) и икосаэдром). Интересно, что согласно многочисленным историческим документам, все они активно использовались жителями Древней Греции в виде настольных игральных костей и изготавливались из самого различного материала.
История фигур
Древняя математическая наука уходит своими корнями в далекое прошлое, во времена процветания Древнего Рима и Греции. Тогда было принято связывать технические аспекты с философскими. Поэтому, согласно учению Платона (один из древнегреческих мыслителей), каждый из многогранников, состоящих из определенного количества одинаковых плоскостей, символизирует одну стихию. Фигуры из треугольников — октаэдр, икосаэдр и тетраэдр — ассоциируются с воздухом, водой и огнем соответственно и могут преобразовываться друг в друга благодаря однотипности граней, каждая из которых имеет три вершины. Землю же символизирует гексаэдр из квадратов. А додекаэдр, благодаря особенным пятиугольным граням, выполняет декоративную роль и является прототипом гармонии и мира.
Также известно, что один из греческих математиков, Евклид, доказал в своем учении «Начала» неповторимость упомянутых платоновых тел и их свойство «вписываться» в сферу (фото 2). Сделан показанный из бумаги многогранник путем сворачивания сомкнутых между собой двадцати равнобедренных треугольников. Схема наглядно демонстрирует выкройку для изготовления фигуры. Рассмотрим подробнее все этапы работы по созданию икосаэдра.
Делаем двадцатигранник
Икосаэдр состоит из одинаковых по размеру равнобедренных треугольников. Его можно легко сложить, используя представленную на рисунке 2 развертку. Возьмите прямоугольный лист бумаги. Начертите на нем двадцать одинаковых по размеру и форме треугольников, расположив их в четырех рядах. При этом каждая грань одного будет одновременно являться стороной другого. Полученный шаблон используйте для изготовления заготовки. Она будет отличаться от основы-развертки наличием припусков для склеивания по всем внешним линиям. Вырезав из бумаги заготовку, согните ее по линиям. Формируя из бумаги многогранник, замыкайте крайние ряды между собой. При этом вершины треугольников соединятся в одну точку.





Что такое тетраэдр
С помощью наглядной объемной фигуры детям проще научиться иметь представление о пространственном мышлении. В этом помогут объемные геометрические фигуры, сделанные своими руками из бумаги. Тетраэдр представляет собой многоугольную фигуру, которая считается простейшей. Он состоит из 4-х граней, каждая из них является равносторонним треугольником. Стороны треугольников соединяются между собой только одной гранью. В фигуре есть также четыре вершины и шесть ребер.
Людей с давних пор привлекали многогранники как удивительные символы симметрии. Они считали их божественными фигурами. Эти фигуры очень важны в развитии математического мышления детей дошкольного и школьного возраста. Они способствуют развитию геометрического представления и пространственного мышления.
На самом деле такая фигура встречается нам повсюду. Однако, сразу ее заметить сложно. Выполненная из стержней, она встречается как основа для пространственных конструкций:
Для того чтобы получить такую фигуру, можно не прибегать к сложным математическим вычислениям. Полученная модель позволит иметь наглядное представление о свойствах геометрической фигуры в объемном изображении.
Правильные многогранники
Все фигуры отличаются друг от друга различным количеством граней и их формой. Кроме этого, некоторые модели могут быть сложены из цельного листа (как описано в примере изготовления икосаэдра), другие – только путем сбора из нескольких модулей. Классическими считаются правильные многогранники. Из бумаги их делают, придерживаясь главного правила симметрии – наличия в шаблоне полностью одинаковых граней. Существует пять основных видов таких фигур. В таблице приведены сведения об их названиях, количестве и формах граней:
| Название | Кол-во граней | Форма каждой грани |
| тетраэдр | 4 | треугольник |
| гексаэдр | 6 | квадрат |
| октаэдр | 8 | треугольник |
| додекаэдр | 12 | пятиугольник |
| икосаэдр | 20 | треугольник |
Юный техник — для умелых рук 1986-12, страница 15
Секреты мастерства 3ВG3ДЧЯТЫв
Приглашаем вас на необычный урок геометрии, где вы научитесь построению звездчатых многогранников. В основе их лежат строгие математические закономерности.
Изготовив хотя бы одну такую звезду, вам, наверное, захочется «открыть» и другие. Своим разнообразием эти геометрические фигуры напоминают фантастические звезды, планеты, астероиды. Причем среди них, вероятно, есть и такие, которые еще никому не удавалось рассчитать и построить. Может, это Сделаете вы? Только начинать работу надо с азов.
Познакомившись с техникой изготовления простых звездчатых многогранников, вы сможете украсить рукотворными звездами актовый зал школы для новогоднего бала, свою комнату, елку. А почему бы не подарить такую звездочку ветерану, другу, не устроить выставку, где вы посоревнуетесь с друзьями в фантазии?
С глубокой древности математикам были известны пять выпуклых многогранников, которые называют Платоновыми телами. Это известные, наверное, каждому школьнику тетраэдр, гексаэдр, октаэдр, икосаэдр, додекаэдр. Этим фигурам в древности приписывали магические свойстза, они олицетворяли землю, воздух, воду, солнце, космос. Их только пять, больше при всем желании не придумаешь.
Каждая из этих фигур образована одинаковыми равносторонними многоугольниками: треугольниками, квадратами, пятиугольниками. Они и являются основой для построения любых звездчатых многогранников.
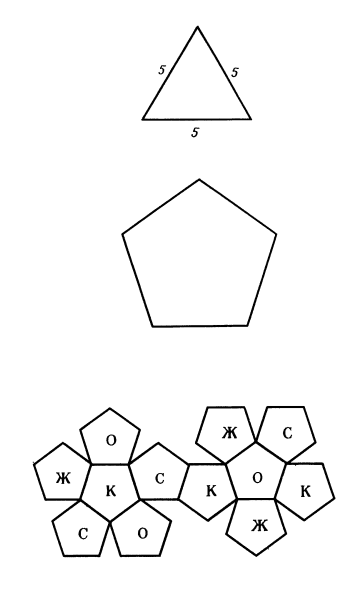
На рисунках 1—5 изображены пять простых многогранников: тетраэдр, гексаэдр, октаэдр, икосаэдр, додекаэдр. Здесь же даны чертежи их граней и возможные варианты разверток для их склейки. Такие грани довольно просто построить, зная основы геометрии.
Элементы для построения звездчатых фигур в основном такие же, только здесь каждая звезда может состоять и из разных граней (см. стр. 16).
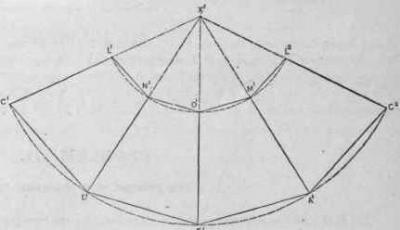
Например, фигуры 6, 7, 8 составлены из одинаковых граней, а вот фигуры 9 и 10 — из двух видов граней. Из нескольких граней можно склеить заготовку для одной из вершин звезды, а после соединить их. Чаще всего грани образованы треугольниками либо квадратами. Сложнее форма граней, показанных на рисунках 8, 9, 10.
По приведенным здесь разверткам получится одна из вершин звезды. Остальные делаются так же.
У звезд 6, 7 и 8 все грани для одной заготовки одинаковы. У звезд 9 и 10 по две формы заготовок и, естественно, две формы вершин.
При изготовлении звезд по рисункам 9 и 10 вы убедитесь, что они получаются из взаимного пересечения двух видов более простых звезд. Так, звезда на рисунке 9 составлена из звезд 6 и 7; а звезда на рисунке 10 — из звезд 7 и 8-
Для изготовления звезд лучше всего применять тонкий цветной картон, наборы которого продаются в магазинах канцтоваров. Можно использовать плотную ватманскую бумагу, отходы от упаковок из картона. Для склеивания применяйте клей ПВА.
Из инструментов вам понадобятся: металлическая линейка, остро заточенный твердый карандаш, шило, чертилка или запиленный под шило гвоздь, вставленный в цанговый карандаш, кисть или тонкая вязальная спица для нанесения клея, ножницы прямые с острыми концами, большие и маленькие, и подкладка из картона, на которой вы будете работать.
Из плотной бумаги или картона сначала изготовьте шаблон одной грани, а лучше — заготовки целиком. С приведенных на наших рисунках разверток переколите их контуры. На изнаночной стороне картона соедините метки карандашом, а потом проведите по полученным линиям кончиком шила.
У каждой заготовки оставьте припуск (клапан) для склейки заготовок по ребрам. Согните заготовки по линиям сгиба на лицо, используя линейку.
Изготовиз полный комплект заготовок, приступайте к склейке вершин. Сначала нужно склеить каждую вершину отдельно. Клей наносится на края граней и на оставленный клапан, детали плотно прижимаются друг к другу до высыхания. После этого можно раскрасить одинаковые вершины. Причем у звезд 9 и 10 вершины разной формы должны быть разного цвета.
Для окончательной сборки звезды осталось склеить вершины друг с другом. При этом некоторые клапаны окажутся лишними, их обрезают. Клеить надо так, чтобы все клапаны оказались внутри. Если развертка выкроена правильно, каждая вершина точно встает на свое место. Трудно бывает приклеить последнюю вершину, но подумав, вы найдете выход из положения.
На этом можно было бы и закончите статью. Но все-таки хочется не ограничиваться рекомендациями, с которыми вы познакомились выше. Попробуйте придумать свою звезду! Какой она получится, посмотрим. Ждем от вас сообщений.
А. БИРЮКОВ, г. Курск Рисунки М. СИМАКОВА










Разнообразие фигур
На основе пяти приведенных видов, используя умение и фантазию, умельцы легко конструируют множество различных моделей из бумаги. Многогранник может совершенно отличаться от вышеописанных пяти фигур, формируясь одновременно из различных по форме граней, например из квадратов и треугольников. Так получаются архимедовы тела. А если одну или несколько граней пропустить, то получится открытая фигура, просматриваемая как снаружи, так и внутри. Для изготовления объемных моделей используются специальные выкройки, вырезаемые из достаточно плотной, хорошо держащей форму, бумаги. Делают и особенные многогранники из бумаги. Схемы таких изделий предусматривают наличие дополнительных, выступающих модулей. Разберем способы, как сконструировать очень красивую фигуру на примере додекаэдра (фото 3).
Схемы и фигуры игры танграм



Вот такой многофункциональный танграм.
Как сделать из бумаги многогранник с двенадцатью вершинами: первый способ
Такую фигуру еще называют звездчатым додекаэдром. Каждая из его вершин в своем основании является правильным пятиугольником. Поэтому делают двумя способами такие многогранники из бумаги. Схемы для изготовления будут несколько отличаться друг от друга. В первом случае это единая деталь (фото 4), в результате сворачивания которой получается готовое изделие. Кроме основных граней, на чертеже присутствуют соединительные части для склеивания, благодаря которым фигура смыкается в единое целое. Для изготовления многогранника вторым способом нужно сделать отдельно несколько шаблонов. Рассмотрим процесс работы подробнее.










Как сделать многогранник из бумаги: второй способ
Изготовьте два главных шаблона (фото 5):
— Первый. Нарисуйте на листе окружность и поделите ее поперек на две части. Одна будет основой для выкройки, дугу второй сразу сотрите для удобства. Поделите деталь на пять равных частей и ограничьте все радиусы поперечными отрезками. В результате получатся соединенные вместе пять одинаковых равнобедренных треугольников. Изобразите рядом примыкающую к среднему отрезку точно такую же полуокружность, только в зеркальном отражении. Полученная деталь при сворачивании выглядит как два конуса. Изготовьте таких аналогичных шаблонов всего шесть штук. Для их склеивания используется вторая деталь, которая будет помещаться вовнутрь.
— Второй. Этот шаблон – пятиконечная звезда. Выполните одинаковые двенадцать заготовок. Формируя многогранник, каждую из звезд с подогнутыми вверх концами помещают внутрь конусообразных деталей и приклеивают к граням.
Полный сбор фигуры получается путем соединения двойных блоков дополнительными отрезками бумаги, заводя их вовнутрь. Моделируя изделия, довольно проблематично сделать их разными по размеру. Готовые модели многогранников из бумаги не так-то просто увеличить. Для этого недостаточно просто сделать припуски по всем внешним границам. Нужно масштабировать отдельно каждую из граней. Только так возможно получить увеличенную копию первоначальной модели. Используя второй способ изготовления многогранника, сделать это намного проще, так как будет достаточно увеличить первоначальные заготовки, по которым уже выполняется нужное количество отдельных деталей.
Сборник «Инструкции по изготовлению моделей правильных и некоторых полуправильных многогранников»
Столичный центр образовательных технологий г. Москва
Получите квалификацию учитель математики за 2 месяца
от 3 170 руб. 1900 руб.
Количество часов 300 ч. / 600 ч.
Успеть записаться со скидкой
Форма обучения дистанционная
МКОУ «Средняя общеобразовательная школа №4»
Изготовление моделей правильных
и некоторых полуправильных многогранников.
v Усеченный тетраэдр
v Усеченный октаэдр
v Усеченный икосаэдр
v Усеченный додекаэдр

Алгоритм построения правильного треугольника:
1. Для построения правильного треугольника АВС, с помощью линейки начертим отрезок АВ, это будет одна из сторон треугольника, а точки А и В его вершинами.
2. Используя циркуль, начертим окружность, центр которой будет в точке А, а радиус равен отрезку АВ.
3. С помощью циркуля начертим еще одну окружность, центр которой будет в точке В, а радиус равен отрезку ВА.
4. Окружности будут пересекаться в двух точках. Выберем любую из них. Назовем ее С. Эта точка будет третьей вершиной треугольника.
5. Соединим вершины между собой. Получившийся треугольник будет правильным.

Алгоритм построения квадрата:
1. Проведите прямую а, на ней отметьте точки А и В. Отрезок АВ будет стороной квадрата.
2. Сейчас нужно провести два перпендикуляра к прямой а, проходящих через точки А и В.
3. Чертим окружность с произвольным радиусом с центром в точке А. Точки пересечения прямой а и окружности обозначаем Р и Н.
4. Строим две окружности с центрами Р и Н радиусом РН. Одну из точек пересечения данных окружностей обозначаем К.
5. Строим прямую АК. Она и будет перпендикулярна прямой а.
7. Аналогично строим перпендикуляр к прямой а, проходящий через точку В. На нем строим отрезок ВС, равный стороне квадрата.

Алгоритм построения правильного треугольника:
1. Для построения правильного треугольника АВС, с помощью линейки начертим отрезок АВ, это будет одна из сторон треугольника, а точки А и В его вершинами.
2. Используя циркуль, начертим окружность, центр которой будет в точке А, а радиус равен отрезку АВ.
3. С помощью циркуля начертим еще одну окружность, центр которой будет в точке В, а радиус равен отрезку ВА.
4. Окружности будут пересекаться в двух точках. Выберем любую из них. Назовем ее С. Эта точка будет третьей вершиной треугольника.
5. Соединим вершины между собой. Получившийся треугольник будет правильным.


Алгоритм построения правильного треугольника:
1. Для построения правильного треугольника АВС, с помощью линейки начертим отрезок АВ, это будет одна из сторон треугольника, а точки А и В его вершинами.
2. Используя циркуль, начертим окружность, центр которой будет в точке А, а радиус равен отрезку АВ.
3. С помощью циркуля начертим еще одну окружность, центр которой будет в точке В, а радиус равен отрезку ВА.
4. Окружности будут пересекаться в двух точках. Выберем любую из них. Назовем ее С. Эта точка будет третьей вершиной треугольника.
5. Соединим вершины между собой. Получившийся треугольник будет правильным.


Алгоритм построения правильного пятиугольника:
1. В первую очередь необходимо построить окружность с центром в точке O.
2. Проведите произвольный диаметр окружности.
3. Далее необходимо построить еще один диаметр, перпендикулярный построенному диаметру. Для этого строим окружность произвольного радиуса с центром в точке О. Построенная окружность пересекает диаметр в точках Р и Н.
4. Постройте окружности с центрами Р и Н, радиусом РН. Эти окружности пересекутся в двух точках.
5. Постройте прямую, проходящую через эти две точки (она так же пройдет через точку О). Данная прямая будет перпендикулярна диаметру.
6. В точке пересечения этой прямой с окружностью поставьте точку V. Эта точка будет вершиной будущего пятиугольника. В точке пересечения другого диаметра с окружностью расположите точку D.
8. После этого нужно построить окружность с центром в точке А. Кроме того, она должна проходить через точку V, то есть, радиусом АV. Точку пересечения диаметра и этой окружности обозначьте В.
9. Проведите окружность такого же радиуса, с центром в точке V. Точку пересечение этой окружности с первоначальной окружностью обозначьте как точку F. Эта точка станет второй вершиной будущего правильного пятиугольника.
11. 

Алгоритм построения правильного шестиугольника:
1. Построить окружность с радиусом, равным стороне будущего шестиугольника.
2. Затем данный радиус последовательно отложить по окружности шесть раз.
Алгоритм построения правильного треугольника:
1. Для построения правильного треугольника АВС, с помощью линейки начертим отрезок АВ, это будет одна из сторон треугольника, а точки А и В его вершинами.
2. Используя циркуль, начертим окружность, центр которой будет в точке А, а радиус равен отрезку АВ.
3. С помощью циркуля начертим еще одну окружность, центр которой будет в точке В, а радиус равен отрезку ВА.
4. Окружности будут пересекаться в двух точках. Выберем любую из них. Назовем ее С. Эта точка будет третьей вершиной треугольника.
5. Соединим вершины между собой. Получившийся треугольник будет правильным.


Алгоритм построения правильного восьмиугольника:
1. Построить окружность с центром в точке О.
2. Провести произвольный диаметр АВ.
7. Соединив данные точки отрезками с точками А и В соответственно, мы получим четыре стороны будущего правильного восьмиугольника.
8. С помощью циркуля отложить на окружности остальные стороны восьмиугольника.
Алгоритм построения правильного треугольника:
1. Для построения правильного треугольника АВС, с помощью линейки начертим отрезок АВ, это будет одна из сторон треугольника, а точки А и В его вершинами.
2. Используя циркуль, начертим окружность, центр которой будет в точке А, а радиус равен отрезку АВ.
3. С помощью циркуля начертим еще одну окружность, центр которой будет в точке В, а радиус равен отрезку ВА.
4. Окружности будут пересекаться в двух точках. Выберем любую из них. Назовем ее С. Эта точка будет третьей вершиной треугольника.
5. Соединим вершины между собой. Получившийся треугольник будет правильным.


Алгоритм построения правильного шестиугольника:
1. Построить окружность с радиусом, равным стороне будущего шестиугольника.
2. Затем данный радиус последовательно отложить по окружности шесть раз.
Алгоритм построения квадрата:
1. Проведите прямую а, на ней отметьте точки А и В. Отрезок АВ будет стороной квадрата.
2. Сейчас нужно провести два перпендикуляра к прямой а, проходящих через точки А и В.
3. Чертим окружность с произвольным радиусом с центром в точке А. Точки пересечения прямой а и окружности обозначаем Р и Н.
4. Строим две окружности с центрами Р и Н радиусом РН. Одну из точек пересечения данных окружностей обозначаем К.
5. Строим прямую АК. Она и будет перпендикулярна прямой а.
7. Аналогично строим перпендикуляр к прямой а, проходящий через точку В. На нем строим отрезок ВС, равный стороне квадрата.


Алгоритм построения правильного шестиугольника:
1. Построить окружность с радиусом, равным стороне будущего шестиугольника.
2. Затем данный радиус последовательно отложить по окружности шесть раз.
Алгоритм построения правильного пятиугольника:
1. В первую очередь необходимо построить окружность с центром в точке O.
2. Проведите произвольный диаметр окружности.
3. Далее необходимо построить еще один диаметр, перпендикулярный построенному диаметру. Для этого строим окружность произвольного радиуса с центром в точке О. Построенная окружность пересекает диаметр в точках Р и Н.
4. Постройте окружности с центрами Р и Н, радиусом РН. Эти окружности пересекутся в двух точках.
5. Постройте прямую, проходящую через эти две точки (она так же пройдет через точку О). Данная прямая будет перпендикулярна диаметру.
6. В точке пересечения этой прямой с окружностью поставьте точку V. Эта точка будет вершиной будущего пятиугольник а. В точке пересечения другого диаметра с окружностью расположите точку D.
8. После этого нужно построить окружность с центром в точке А. Кроме того, она должна проходить через точку V, то есть, радиусом АV. Точку пересечения диаметра и этой окружности обозначьте В.
9. Проведите окружность такого же радиуса, с центром в точке V. Точку пересечение этой окружности с первоначальной окружностью обозначьте как точку F. Эта точка станет второй вершиной будущего правильного пятиугольник а.
11. Остается соединить пять вершин правильного пятиугольника.
Развертка усеченного икосаэдра:

Алгоритм построения правильного треугольника:
1. Для построения правильного треугольника АВС, с помощью линейки начертим отрезок АВ, это будет одна из сторон треугольника, а точки А и В его вершинами.
2. Используя циркуль, начертим окружность, центр которой будет в точке А, а радиус равен отрезку АВ.
3. С помощью циркуля начертим еще одну окружность, центр которой будет в точке В, а радиус равен отрезку ВА.
4. Окружности будут пересекаться в двух точках. Выберем любую из них. Назовем ее С. Эта точка будет третьей вершиной треугольника.
5. Соединим вершины между собой. Получившийся треугольник будет правильным.
Алгоритм построения правильного десятиугольника:
1. В первую очередь необходимо построить окружность с центром в точке O.
2. Проведите произвольный диаметр окружности.
3. Далее необходимо построить еще один диаметр, перпендикулярный построенному диаметру. Для этого строим окружность произвольного радиуса с центром в точке О. Построенная окружность пересекает диаметр в точках Р и Н
4. Постройте окружности с центрами Р и Н, радиусом РН. Эти окружности пересекутся в двух точках.
5. Постройте прямую, проходящую через эти две точки (она так же пройдет через точку О). Данная прямая будет перпендикулярна диаметру.
6. В точке пересечения этой прямой с окружностью поставьте точку V. Эта точка будет вершиной будущего десятиугольника . В точке пересечения другого диаметра с окружностью расположите точку D.
8. Построить окружность с центром в точке А, радиусом АО.
9. Построить отрезок V А. Точку пересечения этой прямой с последней окружностью обозначить К.
10. Длина отрезка VK будет равна стороне правильного десятиугольника. Останется лишь последовательно отложить данный отрезок по окружности.
11. Построить окружность с центром в точке А, радиусом АО.
12. Построить отрезок V А. Точку пересечения этой прямой с последней окружностью обозначить К.
13. 
Развертка усеченного додекаэдра:

Алгоритм построения квадрата:
1. Проведите прямую а, на ней отметьте точки А и В. Отрезок АВ будет стороной квадрата.
2. Сейчас нужно провести два перпендикуляра к прямой а, проходящих через точки А и В.
3. Чертим окружность с произвольным радиусом с центром в точке А. Точки пересечения прямой а и окружности обозначаем Р и Н.
4. Строим две окружности с центрами Р и Н радиусом РН. Одну из точек пересечения данных окружностей обозначаем К.
5. Строим прямую АК. Она и будет перпендикулярна прямой а.
7. Аналогично строим перпендикуляр к прямой а, проходящий через точку В. На нем строим отрезок ВС, равный стороне квадрата.
Алгоритм построения правильного треугольника:
1. Для построения правильного треугольника АВС, с помощью линейки начертим отрезок АВ, это будет одна из сторон треугольника, а точки А и В его вершинами.
2. Используя циркуль, начертим окружность, центр которой будет в точке А, а радиус равен отрезку АВ.
3. С помощью циркуля начертим еще одну окружность, центр которой будет в точке В, а радиус равен отрезку ВА.
4. Окружности будут пересекаться в двух точках. Выберем любую из них. Назовем ее С. Эта точка будет третьей вершиной треугольника.
5. Соединим вершины между собой. Получившийся треугольник будет правильным.


Алгоритм построения правильного пятиугольника:
1. В первую очередь необходимо построить окружность с центром в точке O.
2. Проведите произвольный диаметр окружности.
3. Далее необходимо построить еще один диаметр, перпендикулярный построенному диаметру. Для этого строим окружность произвольного радиуса с центром в точке О. Построенная окружность пересекает диаметр в точках Р и Н.
4. Постройте окружности с центрами Р и Н, радиусом РН. Эти окружности пересекутся в двух точках.
5. Постройте прямую, проходящую через эти две точки (она так же пройдет через точку О). Данная прямая будет перпендикулярна диаметру.
6. В точке пересечения этой прямой с окружностью поставьте точку V. Эта точка будет вершиной будущего пятиугольник а. В точке пересечения другого диаметра с окружностью расположите точку D.
8. После этого нужно построить окружность с центром в точке А. Кроме того, она должна проходить через точку V, то есть, радиусом АV. Точку пересечения диаметра и этой окружности обозначьте В.
9. Проведите окружность такого же радиуса, с центром в точке V. Точку пересечение этой окружности с первоначальной окружностью обозначьте как точку F. Эта точка станет второй вершиной будущего правильного пятиугольник а.
11. Остается соединить пять вершин правильного пятиугольника.
Алгоритм построения правильного треугольника:
1. Для построения правильного треугольника АВС, с помощью линейки начертим отрезок АВ, это будет одна из сторон треугольника, а точки А и В его вершинами.
2. 
3. С помощью циркуля начертим еще одну окружность, центр которой будет в точке В, а радиус равен отрезку ВА.
4. Окружности будут пересекаться в двух точках. Выберем любую из них. Назовем ее С. Эта точка будет третьей вершиной треугольника.
5. Соединим вершины между собой. Получившийся треугольник будет правильным.
Схемы геометрических фигур. Как сделать объемные геометрические фигуры из бумаги, развертки для склеивания: куба, конуса, схемы и шаблоны для вырезания цилиндра, пирамиды, треугольника
Как сделать объемные геометрические фигуры из бумаги (схемы, шаблоны)?
Вот несколько схем, по которым можно изготовить объёмные геометрические фигуры.
Самая простая — тетраэдр.
Чуть сложнее будет изготовить октаэдр.
А вот эта объёмная фигура — додекаэдр.
Ещё одна — икосаэдр.
Более подробно об изготовлении объёмных фигур можно посмотреть здесь.
Вот так выглядят объёмные фигуры не в собранном виде:
А вот так выглядят уже готовые:
Из объёмных геометрических фигур можно сделать много оригинальных поделок, в том числе и упаковки для подарка.
Чтобы дети лучше запомнили, какие бывают геометрические фигуры, и знали, как они называются, можно из плотной бумаги или картона сделать объемные геометрические фигуры. Кстати, на основе их можно изготовить красивую подарочную упаковку.
Самое сложное — это разработать и начертить развёртки, нужны хотя бы базовые знания черчения. Можно взять и готовые развёртки и распечатать на принтере.
Чтобы линия сгиба была ровной и острой, можно воспользоваться тупой иглой и металлической линейкой. При проведении линии иголку нужно сильно нагнуть в направлении движения, практически положив её набок.
Это развертка трехгранной пирамиды
Это развертка куба
Это развертка октаэдра (четырехгранной пирамиды)
Это развертка додекаэдра
Это развертка икосаэдра
Вот здесь можно найти шаблоны более сложных фигур (Платоновы Тела, Архимедовы тела, многогранники, полиэдры, разные виды пирамид и призм, простые и косые бумажные модели).
Кстати, чтобы рассчитать параметры пирамиды, можно воспользоваться вот этой программой.
Самостоятельно смастерив из бумаги объёмные фигуры можно не только использовать их для развлечения, но и для обучения.
К примеру, можно наглядно показать ребёнку как выглядит та или иная фигура, дать её подержать в руках.
Либо можно с целью обучения распечатать схемы со специальными обозначениями.
Так предлагаю ниже ознакомиться со семой додекаэдра, как простой, так и с небольшими рисунками, которые только привлекут внимание малыша и обучение сделают более весёлым и занимательным.
Также схему куба можно использовать для обучения цифрам.
Схема пирамиды может помочь усвоить формулы, которые относятся к данной фигуре.
Кроме того, предлагаю ознакомиться со схемой октаэдра.
Схема тетраэдра помимо прочего поможет изучить цвета.
Как вы поняли, вышеприведённые шаблоны необходимо распечатать, вырезать, согнуть по линиям, склеить по специальным узким полосочкам, прилегающим к избранным сторонам.
Прежде чем начать делать объемные геометрические фигуры, нужно представить (или знать как выглядит) фигуру в 3D измерении: сколько граней имеет та или иная фигура.
Сначала необходимо правильно начертить на бумаге фигуру по граням, которые должны быть соединены между собой. У каждой фигуры грани имеют определенную форму: квадрат, треугольник, прямоугольник, ромб, шестиугольник, круг и т.д.
Очень важно, чтобы длина ребер фигуры, которые будут соединены друг с другом имели одинаковую длину, чтобы во время соединения не возникло проблем. Если фигура состоит из одинаковых граней, я бы предложила сделать шаблон во время черчения использовать этот шаблон. Так же можно скачать из интернета готовые шаблоны, распечатать их, согнуть по линиям и соединить (склеить).
Пирамида — развертка. Развертка пирамиды для склеивания. Развертки из бумаги
Прямоугольник, квадрат, треугольник, трапеция и другие – геометрические фигуры из раздела точной науки. Пирамида — это многогранник. Основанием этой фигуры является многоугольник, а боковыми гранями треугольники, имеющие общую вершину, или трапеции. Для полного представления и изучения любого геометрического объекта изготавливают макеты. Используют самый разнообразный материал, из которого выполняется пирамида. Поверхность многогранной фигуры, развернутая на плоскости, называется ее разверткой. Создать макет поможет метод преобразования плоских предметов в объемные многогранники и определенные знания из геометрии. Развертки из бумаги или картона изготовить непросто. Потребуется умение выполнять чертежи по заданным размерам.
Материалы и приспособления
Моделирование и выполнение многогранных объемных геометрических фигур — интересный и захватывающий процесс. Из бумаги можно выполнить большое количество всевозможных макетов. Для работы будут необходимы:
Определение параметров
Прежде всего определим, какой будет пирамида. Развертка данной фигуры является основой для изготовления объемной фигуры. Выполнение работы потребует предельной точности. При неправильном чертеже геометрическую фигуру собрать будет невозможно. Допустим, необходимо изготовить макет правильной треугольной пирамиды.
Любое геометрическое тело обладает определенными свойствами. Данная фигура имеет основанием правильный многоугольник, а ее вершина спроецирована в его центр. В качестве основания выбран равносторонний треугольник. Данное условие определяет название. Боковые ребра у пирамиды – это треугольники, количество которых зависит от выбранного для основания многогранника. В данном случае их будет три. Также важно знать размеры всех составных частей, из которых будет составлена пирамида. Развертки из бумаги выполняются в соответствии с учетом всех данных геометрической фигуры. Параметры будущей модели оговариваются заранее. От этих данных зависит выбор используемого материала.
Как выполняется развертка правильной пирамиды?
Основой модели является лист бумаги или картона. Работу начинают с чертежа пирамиды. Фигура представляется в развернутом виде. Плоское изображение на бумаге соответствует заранее выбранным размерам и параметрам. Правильная пирамида имеет основанием правильный многоугольник, а высота проходит через его центр. Изготавливаем для начала простую модель. В данном случае – это треугольная пирамида. Определяем размеры выбранной фигуры.
Сборка макета
Вырезаем ножницами выполненный рисунок по контуру. Аккуратно сгибаем развертку по всем линиям. Клапаны-трапеции заправляем внутрь фигуры таким образом, чтобы ее грани сомкнулись. Их смазываем клеем. Через тридцать минут клей высохнет. Объемная фигура готова.
Развертка четырехугольной пирамиды
Сначала представим, как выглядит геометрическая фигура, макет которой будем изготавливать. Основанием выбранной пирамиды является четырехугольник. Боковые ребра — треугольники. Для работы используем те же материалы и приспособления, что и в предыдущем варианте. Чертеж выполняем на бумаге карандашом. В центре листа чертим четырехугольник с выбранными параметрами.
Каждую сторону основания делим пополам. Проводим перпендикуляр, который будет являться высотой треугольной грани. Раствором циркуля, равным длине боковой грани пирамиды, делаем на перпендикулярах засечки, установив его ножку в вершину основания. Оба угла одной стороны основания соединяем с полученной точкой на перпендикуляре. В результате получаем в центре чертежа квадрат, на гранях которого нарисованы треугольники. Чтобы зафиксировать модель на боковых гранях, дорисовывают вспомогательные клапаны. Для надежного крепления достаточно полоски сантиметровой ширины. Пирамида готова к сборке.
Завершающий этап выполнения макета
Полученную выкройку фигуры вырезаем по контуру. По начерченным линиям сгибаем бумагу. Сбор объемной фигуры производят путем склеивания. Предусмотренные клапаны смазываем клеем и фиксируем полученную модель.
Объемные макеты сложных фигур
После выполнения простой модели многогранника можно перейти к более сложным геометрическим фигурам. Развертка пирамиды усеченной намного сложнее в выполнении. Ее основаниями являются подобные многогранники. Боковые грани – это трапеции. Последовательность выполнения работы будет такой же, как та, в которой изготавливалась простая пирамида. Развертка будет более громоздкой. Для выполнения чертежа используют карандаш, циркуль и линейку.
Построение чертежа
Развертка пирамиды усеченной выполняется в несколько этапов. Боковой гранью усеченной пирамиды является трапеция, а основаниями — подобные многогранники. Допустим, что это квадраты. На листе бумаги выполняем чертеж трапеции с заданными размерами. Боковые стороны полученной фигуры продлеваем до пересечения. В результате получаем равнобедренный треугольник. Его сторону измеряем циркулем. На отдельном листе бумаги строим окружность, радиусом которой будет измеренное расстояние.
Следующий этап – это построение боковых ребер, которые имеет усеченная пирамида. Развертка выполняется внутри нарисованной окружности. Циркулем измеряют нижнее основание трапеции. На окружности отмечаем пять точек, которые соединяют линии с ее центром. Получаем четыре равнобедренных треугольника. Циркулем измеряем сторону трапеции, нарисованной на отдельном листе. Данное расстояние откладываем на каждой стороне нарисованных треугольников. Полученные точки соединяем. Боковые грани трапеции готовы. Остается только нарисовать верхнее и нижнее основания пирамиды. В данном случае это подобные многогранники – квадраты. К верхнему и нижнему основаниям первой трапеции дорисовываем квадраты. На чертеже изображены все части, которые имеет пирамида. Развертка практически готова. Остается только дорисовать соединительные клапаны на сторонах меньшего квадрата и одной из граней трапеций.
Завершение моделирования
Перед склеиванием объемной фигуры чертеж по контуру вырезают ножницами. Далее развертку аккуратно сгибают по начерченным линиям. Крепежные клапаны заправляем внутрь модели. Их смазываем клеем и прижимаем к граням пирамиды. Модели даем высохнуть.
Изготовление разных моделей многогранников
Выполнение объемных моделей геометрических фигур — увлекательное занятие. Чтобы его досконально освоить, следует начинать с выполнения самых простых разверток. Постепенно переходя от простых поделок к более сложным моделям, можно приступать к созданию самых замысловатых конструкций.
Развёртки геометрических фигур
Большой выбор развёрток простых геометрических фигур.
Первое знакомство детей с бумажным моделированием всегда начинается с простых геометрических фигур, таких как кубик и пирамида. Не у многих получается склеить кубик с первого раза, иногда требуется несколько дней, чтобы сделать поистине ровный и безупречный куб. Более сложные фигуры цилиндр и конус требуют в несколько раз больше усилий нежели простой кубик. Если вы не умеете аккуратно клеить геометрические фигуры, значит и за сложные модели вам ещё рано браться. Займитесь сами и научите своих детей клеть эти «азы» моделирования по готовым развёрткам.
Для начала я, конечно же, предлагаю научиться клеить обычный кубик. Развёртки сделаны для двух кубиков, большого и маленького. Более сложной фигурой является маленький кубик потому, как клеить его сложнее, чем большой.
Итак, начнём! Скачайте развёртки всех фигур на пяти листах и распечатайте на плотной бумаге. Перед тем, как печатать и клеить геометрические фигуры обязательно ознакомьтесь со статьёй о том, как выбрать бумагу и как вообще правильно вырезать, сгибать и клеить бумагу.
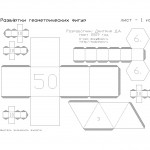
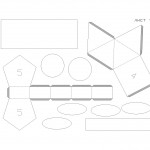
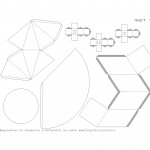
Для более качественной печати советую использовать программу AutoCAD, и даю вам развёртки для этой программы, а также читайте, как распечатывать из автокада. Вырежьте развёртки кубиков с первого листа, по линиям сгиба обязательно проведите иголкой циркуля под железную линейку, чтобы бумага хорошо сгибалась. Теперь можно начинать клеить кубики.
Для экономии бумаги и на всякий пожарный я сделал несколько развёрток маленького кубика, мало ли вам захочется склеить не один кубик или что-то не получится с первого раза. Ещё одна несложная фигура это пирамида, её развёртки найдёте на втором листе. Подобные пирамиды стоили древние египтяне, правда не из бумаги и не таких маленьких размеров 🙂
А это тоже пирамида, только в отличие от предыдущей у неё не четыре, а три грани.
Развёртки трёхгранной пирамиды на первом листе для печати.
И ещё одна забавная пирамидка из пяти граней, её развёртки на 4-ом листе в виде звёздочки в двух экземплярах.
Далее шестигранник, склеить его будет ещё проще, чем пирамиды. Развёртки шестигранника на первом листе.
Более сложная фигура это пятигранник, хотя пятигранник сложнее начертить, нежели склеить.
Развёртки пятигранника на втором листе.
Вот мы и добрались до сложных фигур. Теперь придётся поднапрячься, склеить такие фигуры нелегко! Для начала обычный цилиндр, его развёртки на втором листе.
А это более сложная фигура по сравнению с цилиндром, т.к. в её основании не круг, а овал.
Развёртки этой фигуры на втором листе, для овального основания сделано две запасных детали.
Чтобы аккуратно собрать цилиндр его детали нужно клеить встык. С одной стороны дно можно приклеить без проблем, просто поставьте на стол заранее склеенную трубку, положите на дно кружок и залейте клеем изнутри. Следите, чтобы диаметр трубы и круглого дна плотно подходили друг к другу, без щелей, иначе клей протечёт и всё приклеится к столу. Второй кружок приклеить будет сложнее, поэтому приклейте внутри вспомогательные прямоугольники на расстоянии толщины бумаги от края трубы. Эти прямоугольники не дадут упасть основанию внутрь, теперь вы без проблем приклеете кружок сверху.
Цилиндр с овальным основанием можно клеить также как и обычный цилиндр, но он имеет меньшую высоту, поэтому тут проще вставить внутрь гармошку из бумаги, а наверх положить второе основание и по краю приклеить клеем.
Теперь очень сложная фигура – конус. Его детали на третьем листе, запасной кружок для днища на 4-ом листе. Вся сложность склеивания конуса в его острой вершине, а потом ещё будет очень сложно приклеить дно.
Сложная и одновременно простая фигура это шар. Шар состоит из 12-ти пятигранников, развёртки шара на 4-ом листе. Сначала клеится две половинки шара, а потом обе склеиваются вместе.
Довольно интересная фигура – ромб, её детали на третьем листе.
А теперь две очень похожие, но совершенно разные фигуры, их отличие только в основании.
Когда склеите эти обе фигуры, то не сразу поймёте, что это вообще такое, они получились какие-то совсем невосприимчивые.
Ещё одна интересная фигурка это тор, только он у нас очень упрощён, его детали на 5-ом листе.
И наконец, последняя фигура из равносторонних треугольников, даже не знаю, как это назвать, но фигура похожа на звезду. Развёртки этой фигуры на пятом листе.
На сегодня это всё! Я желаю вам успехов в этой нелёгкой работе!
КОММЕНТАРИИ
Задали по геометрии: тетраэдр, куб, октаэдр, додекаэдр, икосаэдр. Тетраэдр, куб и додекаэдр сделала, а вот оставшиеся две никак(((
Еще возникли трудности с склеиванием..
спасибо, хз че бы делал еслиб не этот сайт =)
Спасибо большое!)))) очень выручили!
Я бы и так не смогла, полезно было ознакомиться.
помогите, как сделать развертку Четырёхугольной пирамиды с основанием — ромб
Как сделать развёртку тора (то есть кольца, вернее, его поверхности)?
Вопрос задан с практической целью, хочу самостоятельно обшить руль машины кожей, но для этого необходимо начертить выкройку, вот тут и возникла трудность — не хватает воображения всё это нарисовать, ведь поверхность тора — это т.н. неразвёртываемая поверхность (вернее, условно-развёртываемая).
Люди, помогите советом или ссылкой, плиз!
Я бы вам посоветовал сходить в магазин и посмотреть как сшиты подобные чехлы для автомобильного руля. Вообще кожа специфический материал, с ней можно делать практически всё, из бумаги такого не сделаешь, поэтому и выкройти тут трудно посоветовать, лучше посмотреть как это уже сделано и дома подумать как сделать своё.
как сделать усечённую пирамиду
Может глупый вопрос, но как сделать из бумаги шар? т.е. не просто круг, а именно объемный шар? есть ли вообще в природе такая развертка?
Развёртка шара из бумаги представляет собой дольки, полоски бумаги сужающиеся по краям. Развёртка шара похожа на рисунок из полосок на арбузе.
Дмитрий, это я тоже помню из курса школьной географии 🙂
А вот как сделать из атласа в электронном виде шар в электронном виде, чтобы потом распечатать и наклеить?
Почему не указаны параметры? Длина, ширина и т.д.?
как сделать цилиндр из бумаги помамогите плиз
Большое человеческое СПАСИБО.
Спасибо вам огромное! Очень нужен был конус. Теперь, благодаря вам, я знаю, как его сделать))
фу
дану это проче простого ещебы квадраты делать учили
мне по технологие задали это
спасибо большое. по геометрии 3 выходит а так 4 :DDD
плохо не чё не пойму
развертка паллалеллограмма неправильная 5 лист
шар не получился там не правильный чертеж
Спасибо большое)))) Ну очень помогли)))
Велике спасибі.Розгортки допомогли мені при виготовленні геометричних фігур на технологіях.
Спасибо большое, хорошие и удобные развёртки)
Проблема с параллелепипедом на пятом листе решается отрезанием косячной грани и её разворотом в правильную сторону)
Развертка фигур. Может развертка геометрических тел?
красиво можно научиться
thank you very much
Спасибо большое! Ребенку во втором класе уже задали эти фигуры. Спасибо Вам за модели, очень удобно, распечатали, сидит, клеит )
Модели конечно интересные, но люди парятся выполняя их, хотя особо труда не составило мне сделать даже сферу. Сыновьям моим (близнецам) задали сделать фигурки из картона, но я то заканчил политех и по начерталке и проходили развертки этих фигур. А у кого гуманитарное образование? Вот у них то и проблемма.
Полезно для изо в 6 классе
Мне кажется, что у Вашего шестигранника восемь граней, а у пятигранника — семь. И называются эти тела либо призмами, либо усеченными пирамидами( в зависимости от соотношения оснований)
Как сделать модель тетраэдра из бумаги и картона
Оригами-тетраэдр из бумаги – эффектный и многофункциональный декоративный элемент. В зависимости от модели, он может служить интерьерной подвеской, ёлочным украшением и частью модного настенного панно в скандинавском стиле. Тетраэдр – четырёхгранная пирамида, в основании которой лежит треугольник. Чаще всего для декора используют несколько таких фигур, объединённых в композицию.
Традиционный вариант
Объёмный тетраэдр-оригами можно сделать из классического квадрата или листа бумаги формата А4. Схема во втором варианте – сложнее, однако для долговечного декора лучше выбирать именно её. Модель получается многослойной, а потому меньше изнашивается в процессе эксплуатации.
Пошаговая инструкция:
Нам понадобится 2 альбомных листа. Складываем их поочерёдно по одному и тому же алгоритму.
Эта модель великолепно смотрится в настенных панно:
Или мобильных подвесках:
Есть и немного другая схема сборки тетраэдра – из одного листа А4. Она представлена в видео-уроке:
Модель от Томоко Касахары
Японский оригамист предлагает сделать модель тетраэдра из квадратного листа. Схема сборки от Касахары настолько подробная, что изготовить по ней фигурку сможет даже начинающий. Для удобства рекомендуется использовать бумагу со сторонами разного цвета – это поможет следить за процессом складывания. Опытные мастера могут брать однотонные листы, что улучшит эстетические качества модели.
Пошаговая инструкция:
Освоив схему сборки тетраэдра Касахары, можно также изготавливать из бумаги своими руками эффектные подарки – разнообразные панно и картины:

Очень простая двухцветная модель
Необычно и эффектно смотрится тетраэдр из двух половинок. Каждую можно сложить из бумаги другого цвета, что сделает геометрический декор ещё интереснее. Если предыдущие модели адресованы, скорее, опытным мастерам, эта – как раз по плечу начинающим.
Пошаговая инструкция:
Аналогичным образом собираем вторую часть. Остаётся склеить двухцветный тетраэдр из бумаги и придумать ему применение.
Декор из картона
Рассматривая варианты оригами-тетраэдра, нельзя обойти вниманием фигуры, изготовленные другим способом, но не менее популярные. Речь идёт о картонных моделях, которые складываются из развёртки, как упаковочные коробочки. Скачиваем трафарет правильного тетраэдра:
Остаётся распечатать его на цветной картон и вырезать заготовки, а затем склеить:
Звёздчатый многогранник
Самая красивая модель получается из нескольких тетраэдров, соединённых между собой. Этот так называемый звёздчатый многогранник, легко сделать своими руками из картона. Тетраэдры собирают из отдельных граней – узких полосок, сложенных «уголком». Именно поэтому нужна не бумага, а плотный картон, иначе ажурная конструкция быстро сомнётся под собственным весом.
Число выступов декоративного кристалла может быть разным. Максимум можно использовать 5 взаимно пересекающихся тетраэдров. Их размер для схемы не важен, но соотношение сторон исходного листа должно составлять 1:3.
Пошаговая инструкция:
Для начала запасаемся листами тонкого дизайнерского картона. Для звезды диаметром 16,5 см нам понадобится 30 прямоугольников размером 5х15 см. Можно выбрать другие параметры, главное, сохранить указанные пропорции. Чтобы не запутаться, рекомендуем делать полосы партиями по 6 штук разного цвета.
Таких заготовок понадобится 30 штук. На лицевой стороне делаем складку «долиной», а на обороте – «горой».
Начинаем сборку пирамидок. Для первой используем 6 красных элементов. Верхний угол намечаем небольшой бумажной полоской, чтобы в дальнейшем упростить себе работу.
Остальные грани собираем и склеиваем по 3 штуки. Тщательно проходим стыки, тогда конструкция получится прочной и долговечной.
К первому красному тетраэдру добавляем полуготовую фигуру из 3-х граней. Ориентируемся на фото-образец. Теперь фиксируем второй – жёлтый тетраэдр, приклеивая ещё 3 недостающие грани.
Аналогичным образом вставляем следующую заготовку, например, голубого цвета и закрепляем её.
Поворачиваем тетраэдр-звезду другой стороной и продолжаем работу.
Следим, чтобы каждая добавленная фигура располагалась под тем же углом, что и остальные.
Последний, фиолетовый, многоугольник крепим с особой тщательностью.
Прежде чем приклеить 3 завершающие грани, несколько раз осматриваем звезду под разными углами. Желательно добиться идеальной симметрии.
Казалось бы, сложная конструкция, на деле требует только аккуратности, внимания и терпения, как и остальные модульные многогранники.
Тетраэдр из картона послужит отличным украшением праздничного интерьера или, например, магазинной витрины.
А эксцентричные невесты вполне могут заменить им свадебный букет.
Звёздчатый многогранник – единственный способ сложить оригами-тетраэдр из модулей. Есть и не менее интересные варианты:
Интересные факты
Тетраэдр – одно из самых интересных, с точки зрения коммерции, платоновых тел. Достаточно простая пирамидка известна каждому с детства. В таких треугольных пакетах – тетропаках во времена СССР продавали молоко, кефир и сливки. Считалось, что благодаря пирамидальной форме деликатная продукция дольше сохраняется свежей.
Треугольная упаковка – совсем не советское изобретение. В 1930-х годах французский научно-популярный журнал «Science & Vie» опубликовал статью о загадочных свойствах египетских пирамид, где тела фараонов не портились, а мумифицировались естественным путём. Теория не подкреплялась серьёзными доказательствами, однако шведский изобретатель Эрик Валленберг настолько увлёкся ею, что создал мини-аналог древнеегипетских усыпальниц – ту самую картонную упаковку Tetra Classic. Он хотел снизить потери молокоторговцев, но на деле оказал помощь производителям одноразовой тары. Его пирамидки выпускались быстро, в больших объёмах и практически без отходов.
В 1950 году на базе инновационной технологии была создана компания AB Tetra Pak. Однако, когда выяснилось, что продукция в картонных пирамидках скисает почти так же быстро, как в стеклянных бутылках, шведы утратили интерес к идее Валленберга. Тем не менее, технологию производства удалось продать советскому руководству, делая упор на её бюджетность и эффективность. Так на наших прилавках появились легендарные «треугольнички» с надписью «Молоко». Чтобы транспортировка пакетов-тетраэдров была не менее выгодной, чем производство, под них изготовили специальные шестиугольные контейнеры.
Сегодня трёхмерные треугольные пакеты (точнее, пакетики) взяла на вооружение компания Lipton. Производитель утверждает, что заменяет плоскую порционную упаковку объёмной, чтобы продемонстрировать красоту раскрывшегося в чашке чайного листа. И показать, что в пакетиках не обрезки и крошка, как подозревают потребители, а полноценный качественный купаж.
Модульное оригами. Многогранник. Мастер-класс с пошаговыми фото
Рад приветствовать вас на своем мастер-классе, в котором я научу вас складывать оригами многогранник из модулей. Для сборки такого многогранника нужно сделать 12 модулей, по 3 модуля красного, синего, желтого и зеленого цвета. Данная модель многогранника собирается без клея, путем соединения модулей в карманчики друг друга. По большому счету, этот многогранник также как и большинство других, входит в класс геометрических кусудам.
Итак, приглашаю вас в мир оригаметрии, ведь наш многогранник из бумаги – это не что иное, как геометрическое тело. Следуйте моим пошаговым фотографиям, и у вас тоже обязательно получится не менее красивая поделка. А теперь давайте посмотрим, что нужно приготовить для ее изготовления. Конечно же, это цветная бумага.
Для этой поделки не обязательно использовать двустороннюю цветную бумагу. Можно воспользоваться и обыкновенной цветной бумагой, но смотрите, чтобы листочки не были слишком тонкими, иначе ваш многогранник быстро помнется.
Для создания этого многогранника в технике модульное оригами нам понадобится:
Модульное оригами многогранник мастер-класс.
Приступим к созданию этой поделки в технике модульное оригами. Берем лист бумаги зеленого цвета, рисуем квадрат 11х11см.
С помощью ножниц вырезаем его.
Нам понадобится для создания зеленых модулей три квадрата.
Подготавливаем остальные квадраты разных цветов.
Приступаем к созданию модуля, берем красный квадрат бумаги.
Складываем наш квадрат пополам, мы получили прямоугольник.
Разворачиваем нашу работу.
Проворачиваем заготовку модуля на 90 градусов вправо и складываем квадрат пополам.
Складываем наш квадрат по диагоналям.
Проворачиваем нашу заготовку модуля на 90 градусов вправо и складываем квадрат по диагоналям, в результате получаем треугольник.
Разворачиваем нашу работу и формируем красный модуль.
По данной методике складываем остальные одиннадцать модулей.
Приступаем к сборке многогранника. Для этого берем четыре разноцветных модуля для создания основания шара.
Собираем красный и зеленый модуль вместе, зелёный модуль заправляем под красный модуль.
К нашим двум модулям прикрепляем синий модуль.
К нашей группе прикрепляем зеленый модуль.
По аналогии закрепляем остальные модули.
Наш многогранник в технике модульное оригами готов.
Среди моих читателей очень много воспитателей Детских садиков и руководителей Художественных кружков, в связи с этим, я изредка публикую посты с поделками вместе с детьми и для детей.
А сейчас, п редлагаю вам занять детей и сделать вместе с ними многогранники из цветной бумаги. Это не только увлечет их, они получат первые знания в математике. Ниже, под катом, пять шаблонов на некоторые многоугольники, которые нужно распечатать и увеличить. Все очень легко и просто, вырезать, согнуть и склеить. Очень красивая гирлянда, яркая, веселая и солнечная)
Во вложении, шаблон мяча в натуральную величину, состоит из восьми страниц.
ДОДЕКАЭДР
ИКОСАЭДР
ОКТАЭДР
ТЕТРАЭДР
Вырезать шаблоны и согнуть по пунктирным линиям
ВУАЛЯ. Можете их собрать на ниточку и сделать математическую гирлянду)
В упаковочке располагаются несколько листов хорошего глянцевого картона с вырубкой цветных деталей, инструкция по сборке и немного исторической информации о фигуре.
Детали очень легко отделяются от общего листа картона. При необходимости места отрыва деталей можно подровнять ножницами. На деталях есть стрелочки, указывающие направление сгиба лепесточков (мест склейки элементов). Для склеивания деталей рекомендуют использовать тот клей, что быстрее схватывается. Мы использовали Супер-ПВА.
Прилагаемая схема сборки многогранника очень подробная, так что ошибиться сложно.
Отмечу, что работа эта кропотливая, и у моего шестилетнего сына не хватило терпения закончить ее. Так что доклеивала мама Галя. Но я ничуть не жалею о приобретении. Во-первых, мы вместе разбирались со схемой, вместе отделяли детали от картона, вместе клеили простые элементы, а это тоже очень важно. При возможности я приобрету еще несколько фигур. А еще подумываю обрадовать нашу бабушку – математика несколькими многогранниками.
Посмотрите, что у нас получилось:
Склеили простые детали. Кстати, они все пронумерованы. Это деталь №1 с донышком №2 – 12 шт
К детали №1 приклеили пять красных треугольников – деталь №3
А потом следующие и следующие…
Для закрепления элементов пришлось использовать прищепки.
Шаг 1. Переносим трафарет и вырезаем фигуры
Загрузите и перенесите трафарет для 15 цветных бумаг. Вырежьте фигуры.
Шаг 2. Складываем фигуры
Сложите бумагу нарисованной стороной внутрь по отпечатанным линиям.
Шаг 3. Отрезаем нитку
Отрежьте 15 ниточек длиной около 60 см и отложите их в сторону.
Шаг 4. Собираем фигуры
Проклейте по одному из отворотов, сложите фигуру и соедините отворот и сторону вместе, пока они не склеятся. Повторите то же самое с другими отворотами, пока все стороны фигуры, за исключением одной, не склеятся.
Шаг 5. Приклеиваем нитку
Отрежьте небольшие кусочки скотча. Положите конец нитки на внешний уголок бумажной фигуры, чтобы он заходил на несколько сантиметров. Сделайте из нитки петельку и закрепите ее скотчем. Благодаря петле будет меньше шансов, что нитка выскочит. Склейте оставшиеся два отворота, чтобы закрыть геометрическую фигуру. Повторите шаги 4 и 5 для всех фигур.
Шаг 6. Распределяем фигуры по местам
У конструкции должно быть пять рядов: в первом ряду одна фигура, во втором – две, в третьем – три и т.д. Расположите фигуры по рядам и по цветам. Проверьте, не запутались ли нитки.
Шаг 7. Собираем конструкцию
Пометьте карандашом на палочке следующие промежутки: 7 см слева, затем восемь интервалов по 4,5 см. Всего должно получиться 9 пометок.
Возьмите первую фигуру в пятом ряду (самом высоком) и повесьте ее на палочку. Фигура должна свешиваться на 15 см вниз. Обмотайте нитку несколько раз и завяжите узелок под палочкой. Отрежьте «хвостик» нитки.
Фигуры в этом ряду будут свешиваться с каждой второй пометки – первой, третьей, пятой, седьмой и девятой. Я хотела, чтобы конструкция выглядела немного по-другому, поэтому повесила фигуры на нитках разной длины. Если вы хотите, чтобы все выглядело ровно, отмерьте и отрежьте нитки одинаковой длины.
Конструкцию будет собрать легче, если вы сможете подвесить ее. Я расположила мою между полкой и столом, попробуйте подвесить свою между спинками стульев.
Четыре фигуры в ряду 4 буду висеть между верхними фигурами, так что привяжите их к палочке на пометках два, четыре, шесть и восемь.
Фигуры ряда 3 привяжите к пометкам три, пять, семь.
Фигуры второго ряда – к пометкам шесть, а первого ряда – к пометке пять.
Повесьте конструкцию под потолок или на стену.
Многогранник из бумаги за 20 минут
Построим двадцать треугольников с равными сторонами по рисунку (я строил треугольники со стороной 15 мм), можно воспользоваться готовым трафаретом. Дочертим «крылышки» для приклеивания граней друг к другу.
По вычерченным сторонам треугольников выдавите желобки для сгибов (тупой стороной ножа по линейке).
Нанесите числа и вырежьте.
Сворачиваем по сгибам и склеиваем.
Осталось доклеить верхние треугольники.
Закрываем последние два треугольника.
Прижимаем «крылышки» внутри булавкой
Построим двенадцать пятиугольников с равными сторонами по рисунку (я строил пятигранники со стороной 10 мм).
Построим восемь треугольников с равными сторонами по рисунку (я строил треугольники со стороной 15 мм).
История фигур
Также известно, что один из греческих математиков, Евклид, доказал в своем учении «Начала» неповторимость упомянутых платоновых тел и их свойство «вписываться» в сферу (фото 2). Сделан показанный из бумаги многогранник путем сворачивания сомкнутых между собой двадцати равнобедренных треугольников. Схема наглядно демонстрирует выкройку для изготовления фигуры. Рассмотрим подробнее все этапы работы по созданию икосаэдра.
Делаем двадцатигранник
Икосаэдр состоит из одинаковых по размеру равнобедренных треугольников. Его можно легко сложить, используя представленную на рисунке 2 развертку. Возьмите прямоугольный лист бумаги. Начертите на нем двадцать одинаковых по размеру и форме треугольников, расположив их в четырех рядах. При этом каждая грань одного будет одновременно являться стороной другого. Полученный шаблон используйте для изготовления заготовки. Она будет отличаться от основы-развертки наличием припусков для склеивания по всем внешним линиям. Вырезав из бумаги заготовку, согните ее по линиям. Формируя из бумаги многогранник, замыкайте крайние ряды между собой. При этом вершины треугольников соединятся в одну точку.
Правильные многогранники
Разнообразие фигур
На основе пяти приведенных видов, используя умение и фантазию, умельцы легко конструируют множество различных моделей из бумаги. Многогранник может совершенно отличаться от вышеописанных пяти фигур, формируясь одновременно из различных по форме граней, например из квадратов и треугольников. Так получаются архимедовы тела. А если одну или несколько граней пропустить, то получится открытая фигура, просматриваемая как снаружи, так и внутри. Для изготовления объемных моделей используются специальные выкройки, вырезаемые из достаточно плотной, хорошо держащей форму, бумаги. Делают и особенные многогранники из бумаги. Схемы таких изделий предусматривают наличие дополнительных, выступающих модулей. Разберем способы, как сконструировать очень красивую фигуру на примере додекаэдра (фото 3).
Как сделать из бумаги многогранник с двенадцатью вершинами: первый способ
Такую фигуру еще называют звездчатым додекаэдром. Каждая из его вершин в своем основании является Поэтому делают двумя способами такие многогранники из бумаги. Схемы для изготовления будут несколько отличаться друг от друга. В первом случае это единая деталь (фото 4), в результате сворачивания которой получается готовое изделие. Кроме основных граней, на чертеже присутствуют соединительные части для склеивания, благодаря которым фигура смыкается в единое целое. Для изготовления многогранника вторым способом нужно сделать отдельно несколько шаблонов. Рассмотрим процесс работы подробнее.
Как сделать многогранник из бумаги: второй способ
Изготовьте два главных шаблона (фото 5):
— Первый. Нарисуйте на листе окружность и поделите ее поперек на две части. Одна будет основой для выкройки, дугу второй сразу сотрите для удобства. Поделите деталь на пять равных частей и ограничьте все радиусы поперечными отрезками. В результате получатся соединенные вместе пять одинаковых равнобедренных треугольников. Изобразите рядом примыкающую к среднему отрезку точно такую же полуокружность, только в зеркальном отражении. Полученная деталь при сворачивании выглядит как два конуса. Изготовьте таких аналогичных шаблонов всего шесть штук. Для их склеивания используется вторая деталь, которая будет помещаться вовнутрь.
Полный сбор фигуры получается путем соединения двойных блоков дополнительными отрезками бумаги, заводя их вовнутрь. Моделируя изделия, довольно проблематично сделать их разными по размеру. Готовые модели многогранников из бумаги не так-то просто увеличить. Для этого недостаточно просто сделать припуски по всем внешним границам. Нужно масштабировать отдельно каждую из граней. Только так возможно получить увеличенную копию первоначальной модели. Используя второй способ изготовления многогранника, сделать это намного проще, так как будет достаточно увеличить первоначальные заготовки, по которым уже выполняется нужное количество отдельных деталей.
Объемные многогранники из бумаги инструкция. Как сделать из бумаги многогранник


- Для изготовления объемных геометрических фигур главное иметь шаблоны, которые можно вырезать, а затем склеить.
Можно сделать из белой или из цветной бумаги. Можно вырезать из бумаги с каким-либо рисунками или же цифрами.
Предлагаю сделать не совсем обычную объемную фигуру в технике оригами. Смотрим видео:
Чтобы дети лучше запомнили, какие бывают геометрические фигуры, и знали, как они называются, можно из плотной бумаги или картона сделать объемные геометрические фигуры
. Кстати, на основе их можно изготовить красивую подарочную упаковку.
Самое сложное — это разработать и начертить развртки, нужны хотя бы базовые знания черчения. Можно взять и готовые развртки и распечатать на принтере.
Чтобы линия сгиба была ровной и острой, можно воспользоваться тупой иглой и металлической линейкой. При проведении линии иголку нужно сильно нагнуть в направлении движения, практически положив е набок.
Это развертка трехгранной пирамиды
Это развертка куба
Это развертка октаэдра (четырехгранной пирамиды)
Это развертка додекаэдра
Это развертка икосаэдра
Вот здесь можно найти шаблоны более сложных фигур (Платоновы Тела, Архимедовы тела, многогранники, полиэдры, разные виды пирамид и призм, простые и косые бумажные модели).
Объемные геометрические фигуры
являются лучшим способом изучение малышом окружающего мира. Отличный учебный материал/отличное учебное пособие для в изучении геометрических фигур — это, как раз, объемные фигуры. Таким способом лучше запоминаются геометрические фигуры.
Лучши материал для изготовления подобных объемных фигур — это плотная бумага (можно цветную) или же картон.
Для изготовления понадобятся кроме бумаги еще и карандаш с линейкой, а также ножницы и клей (вырезать и клеить развертки).
Нужно начертить подобным образом развертки и вырезать их:
После чего их нужно склеивать край к краю.
Должны получится следующего вида объемные геометрические фигуры:
Вот несколько схем, по которым можно изготовить объмные геометрические фигуры.
Самая простая — тетраэдр
Чуть сложнее будет изготовить октаэдр
А вот эта объмная фигура — додекаэдр
Более подробно об изготовлении объмных фигур можно посмотреть здесь.
Вот так выглядят объмные фигуры не в собранном виде:
А вот так выглядят уже готовые:
Из объмных геометрических фигур можно сделать много оригинальных поделок, в том числе и упаковки для подарка.
Прежде чем начать делать объемные геометрические фигуры, нужно представить (или знать как выглядит) фигуру в 3D измерении: сколько граней имеет та или иная фигура.
Сначала необходимо правильно начертить на бумаге фигуру по граням, которые должны быть соединены между собой. У каждой фигуры грани имеют определенную форму: квадрат, треугольник, прямоугольник, ромб, шестиугольник, круг и т.д.
Очень важно, чтобы длина ребер фигуры, которые будут соединены друг с другом имели одинаковую длину, чтобы во время соединения не возникло проблем. Если фигура состоит из одинаковых граней, я бы предложила сделать шаблон во время черчения использовать этот шаблон. Так же можно скачать из интернета готовые шаблоны, распечатать их, согнуть по линиям и соединить (склеить).
Изготовление объемных геометрических фигур вам понадобится как на школьных занятиях, так и для изучения фигур с малышами. Этот процесс можно превратить в игру, делая из картона плотные объемные геометрические фигуры.
Для изготовления фигур нам понадобится — карандаш, линейка, цветной картон, клей.
Можно распечатать схемы из интернета, потом нанести их на плотную бумагу, не забывая про линии сгиба, которые будут склеиваться между собой.
А воспользоваться можно следующими схемами:
А вот они уже в готовом виде.
Так вы весело и с пользой сможете провести с малышом время, изучая геометрические фигуры.
Самостоятельно смастерив из бумаги объмные фигуры можно не только использовать их для развлечения, но и для обучения.
К примеру, можно наглядно показать ребнку как выглядит та или иная фигура, дать е подержать в руках.
Либо можно с целью обучения распечатать схемы со специальными обозначениями.
Так предлагаю ниже ознакомиться со семой додекаэдра
, как простой, так и с небольшими рисунками, которые только привлекут внимание малыша и обучение сделают более веслым и занимательным.
можно использовать для обучения цифрам.
может помочь усвоить формулы, которые относятся к данной фигуре.
Кроме того, предлагаю ознакомиться со схемой октаэдра
помимо прочего поможет изучить цвета.
Как вы поняли, вышеприведнные шаблоны необходимо распечатать, вырезать, согнуть по линиям, склеить по специальным узким полосочкам, прилегающим к избранным сторонам.
Объемные геометрические фигуры просто необходимы при обучении: они предоставляют ученикам возможность держать их в руках, рассматривать, что является важной частью учебного процесса, они просто необходимы в качестве пособия при изучении знаменитой теоремы Эйлера — наглядно демонстрируя, что даже при деформациях, искривлениях число граней многогранника, а значит и соотношение Эйлера, останется неизменным:
Кроме того, объемные фигуры могут служить отличным пособием, помогающим объяснить ученикам, как найти площадь поверхности многогранника.
Итак, с помощью приведенных ниже шаблонов Вы можете легко сделать следующие фигуры:
И еще несколько редких объемных геометрических фигур можно найти по этой ссылке.
Создавать поделки своими руками интересно не только детям, но и взрослым. Однако для взрослых придумано достаточное количество моделей, которые отличаются сложностью выполнения и временем, затраченным на их создание. В последнее время у взрослых и детей появился интерес к созданию сложных геометрических фигур. К такому виду фигур относится икосаэдр, который представляет собой правильный многоугольник и является одним из платоновых тел – правильных многогранников. Эта фигура имеет 20 треугольных граней (равносторонних треугольников), 30 ребер и 12 вершин, которые являются местом стыка 5 ребер. Правильный икосаэдр из бумаги собрать достаточно сложно, но интересно. Если вы увлечены оригами, то сделать икосаэдр бумажный своими руками вам не составит труда. Его сделать из цветной, гофрированной бумаги, фольги, упаковочной бумаги для цветов. Используя разнообразные материалы, можно придать еще большую красоту и эффектность своему икосаэдру. Все зависит только от фантазии его создателя и подручного материала, имеющегося на столе.
Предлагаем вам несколько вариантов разверток икосаэдра, которые можно распечатать, перенести на плотную бумагу и картон, согнуть по линиям и склеить.
Как сделать икосаэдр из бумаги: схема
Для того чтобы собрать икосаэдр из листа бумаги или картона, необходимо предварительно подготовить следующие материалы:
Во время создания икосаэдра важно обратить особое внимание на процесс сгиба всех деталей: для того, чтобы ровно согнуть бумагу, можно использовать обычную линейку.
Примечательно, что икосаэдр можно встретить и в повседневной жизни. Например, в форме усеченного икосаэдра (многогранник, состоящий из 12 пятиугольников и 20 шестиугольников правильной формы) выполнен футбольный мяч. Это особенно видно, если раскрасить получившийся икосаэдр в черно-белый цвет, как и сам мяч.
Такой футбольный мяч можно сделать самостоятельно, распечатав предварительно развертку усеченного икосаэдра в 2 экземплярах:
Создание икосаэдра своими руками представляет интересный процесс, который требует вдумчивости, терпения и большого количества бумаги. Однако результат, полученный в итоге, будет радовать глаз еще долгое время. Икосаэдр можно дать поиграть ребенку, если он достиг уже трехлетнего возраста. Играя с такой сложной геометрической фигурой, он будет развивать не только образное мышление, пространственные навыки, но и знакомиться с миром геометрии. Если же взрослый решил создать икосаэдр самостоятельно, то такой творческий процесс по конструированию икосаэдра позволит скоротать время, а также похвастаться перед близкими своим умением создавать сложные фигуры.
Много интересного можно найти для себя в тех сферах науки, которые, казалось бы, никогда не пригодятся в привычной жизни простого обывателя. Например, геометрия, о которой большинство забывают, только лишь переступив порог школы. Но странным образом малознакомые области науки становятся очень увлекательными, если с ними столкнуться поближе. Вот и геометрическая развертка многогранника — совершенно ненужная в повседневной жизни вещь — может стать началом увлекательного творчества, способного захватить и детей, и взрослых.
Красивая геометрия
Украшать интерьер дома, создавая своими руками необычные, стильные вещи, — это увлекательное творчество. Смастерить самостоятельно из плотной бумаги различные многогранники — значит создать уникальные вещи, которые могут стать просто занятием на день или два, а могут превратиться в дизайнерские интерьерные украшения. К тому же с развитием техники, способной к пространственному моделированию всевозможных вещей, стало возможным создание стильных и современных 3D-моделей. Есть мастера, которые при помощи простроения разверток по законам геометрии делают из бумаги макеты животных и различных предметов. Но это достаточно сложное математическое и чертежное творчество. Начать работать в подобной технике поможет
Разные грани — разные формы
Многогранники — это особая сфера геометрии. Они бывают простые — к примеру кубики, которыми дети играют с раннего возраста, — а бывают очень и очень сложные. Простроение развертки многогранников для склеивания считается достаточно сложной областью конструирования и творчества: нужно не только знать основы черчения, геометрические особенности пространства, но и иметь пространственное воображение, позволяющее оценить правильность решения еще на стадии проектирования. Но и одной фантазией не обойтись. Чтобы сделать развертки не достаточно просто представить, как в конце концов должна выглядеть работа. Нужно уметь правильно ее просчитать, сконструировать, а также грамотно начертить.
Самый первый многогранник — кубик
Скорее всего, каждый человек, посещавший школу, еще в начальных классах сталкивался на уроках труда с работой, результатом которой должен был стать бумажный кубик. Чаще всего учительница раздавала заготовки — развертки многогранника куба на плотной бумаге со специальными кармашками, предназначенными для склеивания граней модели в единое целое. Такой работой ученики начальной школы могли гордиться, ведь при помощи бумаги, ножниц, клея и своих усилий получалась интересная поделка — трехмерный куб.
Занимательные грани
Удивительно, но многие знания об окружающем мире становятся интересны не на школьной скамье, а лишь тогда, когда можно найти в них нечто увлекательное, способное дать что-то новое, необычное в привычной жизни. Не многие взрослые помнят, что те же многогранники делятся на огромное количество видов и подвидов. Например, есть так называемые платоновы тела — выпуклые многогранники, состоящие только лишь из Таких тел всего пять: тетраэдр, октаэдр, гексаэдр (куб), икосаэдр, додекаэдр. Они представляют собой выпуклые фигуры без впадин. Звездчатые многогранники состоят из этих основных фигур в различных конфигурациях. Поэтому-то развертка многогранника простого позволяет нарисовать, вернее начерить, а затем и склеить из бумаги звездчатый многогранник.
Историческая справка
Как выше было сказано, додекаэдр — это одно из пяти платоновых тел, которые характеризуются тем, что образованы одинаковыми правильными многогранниками. Остальными четырьмя платоновыми телами являются тетраэдр, октаэдр, куб и икосаэдр.
Упоминания о додекаэдре относятся еще к вавилонской цивилизации. Однако первое подробное изучение его геометрических свойств сделали древнегреческие философы. Так, Пифагор в качестве эмблемы своей школы использовал пятиконечную звезду, построенную на вершинах пентагона (грани додекаэдра).
Платон подробно охарактеризовал правильные объемные фигуры. Философ считал, что они представляют главные стихии: тетраэдр — это огонь; куб — земля; октаэдр — воздух; икосаэдр — вода. Поскольку додекаэдру не досталась никакая стихия, то Платон предположил, что он описывает развитие всей Вселенной.
Мысли Платона многие могут посчитать примитивными и псевдонаучными, однако вот что любопытно: современные исследования наблюдаемой Вселенной показывают, что приходящее на Землю космическое излучение обладает анизотропией (зависимостью от направления), и симметрия этой анизотропии хорошо согласуется с геометрическими свойствами додекаэдра.
Правильные и неправильные звездчатые многогранники
Складывая платоновые тела между собой в определенном порядке, вы можете построить немало звездчатых многоранников — красивых, сложных, многокомпонентных. Но они будут называться «неправильными звездчатыми многогранниками». Правильных звездчатых многогранников всего четыре: малый звездчатый додекаэдр, большой звездчатый додекаэдр, большой додекаэдр и большой икосаэдр. Развертки многогранников для склеивания не будут простыми чертежами. Они, как и фигуры, будут состоять из нескольких компонентов. Так, например, малый звездчатый додекаэдр строится из 12 пятиугольных равнобочных пирамид, сложенных по типу правильного додекаэдра. То есть для начала придется начертить и склеить 12 одинаковых штук правильных пирамид, состоящих из 5 равных граней. И только затем из них можно сложить звездчатый многогранник. Развертка самого малого звездчатого додекаэра — сложное и практически невыполнимое задание. Чтобы ее простроить, нужно суметь на одной плоскости уместить соединенные друг с другом 13 разверток разных геометрических объемных тел.
Кусудама из правильных пятиугольников
Схема сборки додекаэдра-оригами из пентагонов – равносторонних пятиугольников, разработана американским дизайнером Дэвидом Брилом. Для модулей он использует 12 листов формата А6, то есть 10,5х14,8 см.
Пошаговая инструкция:
Из подобных додекаэдров часто делают настольные календари. На каждой грани как раз размещается по месяцу. Соответствующие распечатки с числами и днями недели, можно скачать из интернета и наклеить на стенки модели. Получится не только красиво, но и практично.
Красота в простоте
Все объемные тела, построенные по законам геометрии, будут смотреться завораживающе, в том числе и звездчатый многогранник. Развертка каждого элемента любого подобного тела должна быть выполнена максимально точно. И даже самые простые объемные многогранники, начиная с платонового тетраэдра, — удивительная красота гармонии мироздания и труда человека, воплощенного в бумажной модели. Вот, допустим, самый многогранный из платоновых выпуклых многогранников — додекаэдр. В этой геометрической фигуре 12 абсолютно одинаковых граней, 30 ребер и 12 вершин.Чтобы сделать развертки правильных многогранников для склеивания, нужно приложить максимум аккуратности и внимательности. И чем крупнее фигура по размерам, тем точнее должны быть все измерения.
Природные формы и использование
Многие микроорганизмы, в том числе вирусы, имеют икосаэдрические оболочки. Их структуры построены из повторяющихся идентичных белковых субъединиц, и икосаэдр является самой лёгкой формой для их сборки. Используется обычный тип многогранника, поскольку он может быть построен из одного базового белка, который будет использоваться снова и снова. Это очень упрощает жизнь и экономит место в вирусном геноме.
А также были обнаружены различные органеллы бактериальной клетки с икосаэдрической формой. В 1904 году Эрнст Геккель описал ряд видов радиолярий, чей скелет имеет форму и свойства многогранника. Икосаэдрическое двойникование также происходит в кристаллах, особенно в наночастицах.
К другим примерам того, как природа использует такую структуру для достижения многих целей, можно отнести инклюзионные тела — компартменты, которые образуются внутри клеток, обычно во время некоторых фаз роста или в определённых условиях окружающей среды.
Использование икосаэдров для разделения пространства и контроля доступа очень эффективно и, по-видимому, предпочтительно, когда ресурсы организмов ограничены.
В древности игральные кости имели столько сторон, сколько граней в икосаэдре. Такие двадцатигранные кубики могли быть пронумерованы от 0 до 9 дважды или от 1 до 20. Форма правильных многогранников часто используется для создания различных предметов в компьютерных играх и головоломках. В виртуальном мире, кстати, часто можно встретить и другие геометрические тела. Например, в «Супер Марио Галактике» планеты имеют форму, похожую на ромбоусечённый икосододекаэдр — архимедово тело.
Японский картограф Содзи Садао и американский архитектор Ричард Бакминстер Фуллер разработали карту мира в виде развёрнутого икосаэдра. Этот же многогранник лежит в основе геодезических сеток, которыми пользуются метеорологи и климатологи.
Как построить развертку самостоятельно?
Пожалуй, помимо склеивания многогранника — хоть звездчатого, хоть платоновского, — еще интереснее построить развертку будущей модели собственными силами, оценив свои способности к черчению, конструированию и пространственному вообжению. Простые платоновсткие тела состоят из простых многоугольников, которые в одной фигуре идентичны друг другу. Так, тетраэдр — это три равнобедренных треугольника. Прежде чем простроить развертку, нужно представить себе, как правильно сложить плоские многоугольники между собой, чтобы получить многогранник. Треугольники можно соединить между собой по ребрам, прочертив один рядом с другим. Для склеивания развертки многогранников схемы должны быть снабжены специальными кармашками или клапанами, которые позволят соединить все части в единое целое. Тетраэдр — простейшая фигура из четырех граней. Октаэдр можно представить как двойной тетраэдр, у него восемь гарней — равнобедренных треугольников. Гексаэдром называют знакомый всем с детства куб. Икосаэдр представляет собой соединение 20 равнобедренных треугольников в правильный выпуклый многогранник. Додекаэдр — это объемная фигура из 12 граней, каждая из которых представляет собой правильный пятиугольник.
Симметрия правильного додекаэдра
Как видно из рисунка выше, додекаэдр — это достаточно симметричная фигура. Для описания этих свойств в кристаллографии вводят понятия об элементах симметрии, главными из которых являются поворотные оси и плоскости отражения.
Идея использования этих элементов проста: если установить ось внутри рассматриваемого кристалла, а затем повернуть его вокруг этой оси на некоторый угол, то кристалл полностью совпадет сам с собой. То же самое относится к плоскости, только операцией симметрии здесь является не поворот фигуры, а ее отражение.
Для додекаэдра характерны следующие элементы симметрии:
Тонкости работы
Построить разверту многогранника и склеить из нее бумажную модель — дело тонкое. Развертку, конечно, можно взять уже готовую. А можно, приложив услилия, построить ее самостоятельно. Но чтобы сделать полноценную объемную модель многогранника, нужно ее собрать. Многогранник лучше всего делать из плотной бумаги, которая хорошо держит форму и не коробится от клея. Все линии, которые необходимо согнуть, лучше всего предварительно продавить, используя, например, непишущую шариковую ручку или обратную сторону лезвия ножа. Этот нюанс поможет сложить модель аккуратнее, с соблюдением размеров и направлений ребер.
Если сделать разные многогранники из цветной бумаги, то такие модели можно использовать в качестве декоративных элементов, украшающих помещение — детскую комнату, кабинет, гостиную. Кстати, многогранники можно назвать уникальной находкой декораторов. Современные материалы позволяют на основе геометрических фигур создавать оригинальные предметы интерьера.
Бумажные поделки — это не только различные открытки и аппликации, выполненные в виде плоских изделий. Очень оригинальными получаются объемные модели фигур (фото 1). Например, можно сконструировать Рассмотрим некоторые способы его выполнения, используя схемы и фотографии.
Оригами додекаэдр
Одной из простейших бумажных кусудам считается додекаэдр-оригами. Но это не значит, что он выглядит неэффектно, особенно когда речь идёт о звёздчатой разновидности. Декоративный многогранник, подобно другим своим родственникам – кусудамам, отлично подходит для праздничного украшения помещений или в качестве оригинального подарка. Мини-додекаэдры можно использовать как модные украшения, сделав из них серьги или кулон.
История фигур
Древняя математическая наука уходит своими корнями в далекое прошлое, во времена процветания Древнего Рима и Греции. Тогда было принято связывать технические аспекты с философскими. Поэтому, согласно учению Платона (один из древнегреческих мыслителей), каждый из многогранников, состоящих из определенного количества одинаковых плоскостей, символизирует одну стихию. Фигуры из треугольников — октаэдр, икосаэдр и тетраэдр — ассоциируются с воздухом, водой и огнем соответственно и могут преобразовываться друг в друга благодаря однотипности граней, каждая из которых имеет три вершины. Землю же символизирует гексаэдр из квадратов. А додекаэдр, благодаря особенным пятиугольным граням, выполняет декоративную роль и является прототипом гармонии и мира.
Также известно, что один из греческих математиков, Евклид, доказал в своем учении «Начала» неповторимость упомянутых платоновых тел и их свойство «вписываться» в сферу (фото 2). Сделан показанный из бумаги многогранник путем сворачивания сомкнутых между собой двадцати равнобедренных треугольников. Схема наглядно демонстрирует выкройку для изготовления фигуры. Рассмотрим подробнее все этапы работы по созданию икосаэдра.
Современное использование додекаэдра
В настоящее время геометрические объекты в форме додекаэдра находят применение в некоторых сферах деятельности человека:
Делаем двадцатигранник
Икосаэдр состоит из одинаковых по размеру равнобедренных треугольников. Его можно легко сложить, используя представленную на рисунке 2 развертку. Возьмите прямоугольный лист бумаги. Начертите на нем двадцать одинаковых по размеру и форме треугольников, расположив их в четырех рядах. При этом каждая грань одного будет одновременно являться стороной другого. Полученный шаблон используйте для изготовления заготовки. Она будет отличаться от основы-развертки наличием припусков для склеивания по всем внешним линиям. Вырезав из бумаги заготовку, согните ее по линиям. Формируя из бумаги многогранник, замыкайте крайние ряды между собой. При этом вершины треугольников соединятся в одну точку.
Бумажная модель
Используя 30 квадратных листов бумаги (размер каждой стороны 7,5 см), можно сделать довольно крепкую версию одной из разновидности этого геометрического чуда совсем без склеивания. Если в запасе есть материал разного цвета, то получится яркий и красивый макет с разноцветными блоками. Инструкция по изготовлению звездчатого икосаэдра поэтапно:
Всего таких блоков нужно сделать 30. Например, по 10 разного цвета.
Правильные многогранники
Все фигуры отличаются друг от друга различным количеством граней и их формой. Кроме этого, некоторые модели могут быть сложены из цельного листа (как описано в примере изготовления икосаэдра), другие — только путем сбора из нескольких модулей. Классическими считаются правильные многогранники. Из бумаги их делают, придерживаясь главного правила симметрии — наличия в шаблоне полностью одинаковых граней. Существует пять основных видов таких фигур. В таблице приведены сведения об их названиях, количестве и формах граней:
Разнообразие фигур
На основе пяти приведенных видов, используя умение и фантазию, умельцы легко конструируют множество различных моделей из бумаги. Многогранник может совершенно отличаться от вышеописанных пяти фигур, формируясь одновременно из различных по форме граней, например из квадратов и треугольников. Так получаются архимедовы тела. А если одну или несколько граней пропустить, то получится открытая фигура, просматриваемая как снаружи, так и внутри. Для изготовления объемных моделей используются специальные выкройки, вырезаемые из достаточно плотной, хорошо держащей форму, бумаги. Делают и особенные многогранники из бумаги. Схемы таких изделий предусматривают наличие дополнительных, выступающих модулей. Разберем способы, как сконструировать очень красивую фигуру на примере додекаэдра (фото 3).
Римский додекаэдр
В середине XVIII века в результате некоторых археологических раскопок на территории Европы был найден странный предмет: он имел форму додекаэдра, сделанного из бронзы, его размеры составляли несколько сантиметров, и он был пустым внутри. Однако любопытно следующее: в каждой его грани было сделано отверстие, причем диаметр всех отверстий был различным. В настоящее время найдено более 100 таких объектов в результате раскопок во Франции, Италии, Германии и других стран Европы. Все эти предметы датируются II-III веком нашей эры и относятся к эпохе господства Римской Империи.
Как римляне использовали эти предметы — не известно, поскольку не найдено ни одного письменного источника, который бы содержал точное объяснение их назначения. Лишь в некоторых трудах Плутарха можно встретить упоминание, что эти объекты служили для понимания характеристик 12-ти знаков Зодиака. Современное объяснение тайны римских додекаэдров имеет несколько версий:
Существуют и другие версии использования римских додекаэдров, тем не менее ни одна из них не имеет точных доказательств. Известно лишь одно: древние римляне высоко ценили эти предметы, поскольку в раскопках они часто обнаруживаются в тайниках вместе с золотом и драгоценностями.
Как сделать из бумаги многогранник с двенадцатью вершинами: первый способ
Такую фигуру еще называют звездчатым додекаэдром. Каждая из его вершин в своем основании является Поэтому делают двумя способами такие многогранники из бумаги. Схемы для изготовления будут несколько отличаться друг от друга. В первом случае это единая деталь (фото 4), в результате сворачивания которой получается готовое изделие. Кроме основных граней, на чертеже присутствуют соединительные части для склеивания, благодаря которым фигура смыкается в единое целое. Для изготовления многогранника вторым способом нужно сделать отдельно несколько шаблонов. Рассмотрим процесс работы подробнее.









Как сделать правильный додекаэдр своими руками
Сегодня конструкция данной фигуры нашла свое отображение во многих вариантах художественного творчества, архитектуре и строительстве. Народные умельцы изготавливают из цветной или белой бумаги необыкновенные по красоте оригами в виде ажурных додекаэдров, а из картона делают оригинальные и прочее). В продаже можно приобрести уже готовые наборы, содержащие все необходимое для изготовления сувениров, но наиболее интересно произвести весь процесс работы своими руками, начиная от построения отдельных деталей и заканчивая сборкой готовой конструкции.
Материалы:
Для того, чтобы сделать правильный додекаэдр из картона, необходим собственно сам материал и подручные средства:
Как сделать многогранник из бумаги: второй способ
Изготовьте два главных шаблона (фото 5):
Нарисуйте на листе окружность и поделите ее поперек на две части. Одна будет основой для выкройки, дугу второй сразу сотрите для удобства. Поделите деталь на пять равных частей и ограничьте все радиусы поперечными отрезками. В результате получатся соединенные вместе пять одинаковых равнобедренных треугольников. Изобразите рядом примыкающую к среднему отрезку точно такую же полуокружность, только в зеркальном отражении. Полученная деталь при сворачивании выглядит как два конуса. Изготовьте таких аналогичных шаблонов всего шесть штук. Для их склеивания используется вторая деталь, которая будет помещаться вовнутрь.
Этот шаблон — пятиконечная звезда. Выполните одинаковые двенадцать заготовок. Формируя многогранник, каждую из звезд с подогнутыми вверх концами помещают внутрь конусообразных деталей и приклеивают к граням.
Полный сбор фигуры получается путем соединения двойных блоков дополнительными отрезками бумаги, заводя их вовнутрь. Моделируя изделия, довольно проблематично сделать их разными по размеру. Готовые модели многогранников из бумаги не так-то просто увеличить. Для этого недостаточно просто сделать припуски по всем внешним границам. Нужно масштабировать отдельно каждую из граней. Только так возможно получить увеличенную копию первоначальной модели. Используя второй способ изготовления многогранника, сделать это намного проще, так как будет достаточно увеличить первоначальные заготовки, по которым уже выполняется нужное количество отдельных деталей.
Как сделать многогранник?
Необходимость сделать многогранник возникает нечасто, однако случается, что ребёнку на дом задают это задание или вы решаете сделать оригинальный подарок другу. А возможно, у вас возникла какая-то дизайнерская задумка. Так или иначе, понадобился многогранник из бумаги. Как его склеить?
Ажурная модель
Существует несколько типов оригами-додекаэдров, но сделать эту прозрачную конструкцию из бумажных модулей проще всего. Хорошее задание для детей, желающих познакомиться с азами пространственной геометрии и взрослых, ищущих эффективное средство для снятия стресса. Желательно использовать для игрушки бумагу ками с рисунком, она придаст особый шарм и колорит.
Пошаговая инструкция:
Остаётся соединить их в пространственную композицию. Для этого короткую часть одного модуля вставляем к «карман» длинной части другого. И располагаем так, чтобы внутренние углы и грани обоих элементов совпали.
Аналогичный образом добавляем третий модуль, соединяя его с предыдущими двумя и формируя устойчивый конструктивный узел.
Продолжаем крепить детали друг к другу, пока не получится объёмная фигура.
За счёт необычной бумаги с принтом, получается стильный предмет декора. Чтобы кусудама не распадалась, лучше соединить узловые элементы с помощью клея.
Подробная сборка ажурного додекаэдра представлена и в видео-МК:
Источники информации:
- http://dockamaster.ru/iz-kartona-i-bumagi/origami-geometricheskie-figury-iz.html
- http://www.craft-retro.ru/2020/06/mnogogranniki-iz-bumagi.html
- http://piko-train.ru/iz-bumagi/mnogogranniki-iz.html
- http://infourok.ru/sbornik-instrukcii-po-izgotovleniyu-modeley-pravilnih-i-nekotorih-polupravilnih-mnogogrannikov-1814539.html
- http://igrad.su/vse-zapisi/shemy-geometricheskih-figur-kak-sdelat-obemnye-geometricheskie-figury-iz-bumagi-razvertki-dlya-skleivaniya-kuba-konusa-shemy-i-shablony-dlya-vyrezaniya-tsilindra-piramidy-treugolnika.html
- http://all-origami.ru/kak-sdelat-model-tetraedra-iz-bumagi-i-kartona/
- http://masterclassy.ru/origami/modulnoe-origami/8418-modulnoe-origami-mnogogrannik-master-klass-s-poshagovymi-foto.html
- http://groundd.ru/medicinal-plants/mnogogranniki-svoimi-rukami-shemy-kak-sdelat-krasivye-bumazhnye-mnogogranniki-eshch-odin-sposob-izgo.html
- http://hozyaika-mama.ru/iz-bumagi/mnogogrannik-iz-shema.html