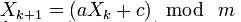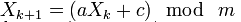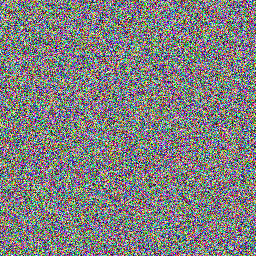Как сделать чтобы генератор случайных чисел выбрал нужное число

Подробно о генераторах случайных и псевдослучайных чисел

Введение

Как отличить случайную последовательность чисел от неслучайной?

Чуть более сложный пример или число Пи

Последовательность цифры в числе Пи считается случайной. Пусть генератор основывается на выводе бит представления числа Пи, начиная с какой-то неизвестной точки. Такой генератор, возможно и пройдет «тест на следующий бит», так как ПИ, видимо, является случайной последовательностью. Однако этот подход не является критографически надежным — если криптоаналитик определит, какой бит числа Пи используется в данный момент, он сможет вычислить и все предшествующие и последующие биты.
Данный пример накладывает ещё одно ограничение на генераторы случайных чисел. Криптоаналитик не должен иметь возможности предсказать работу генератора случайных чисел.

Отличие генератора псевдослучайных чисел (ГПСЧ) от генератора случайных чисел (ГСЧ)

Источники энтропии используются для накопления энтропии с последующим получением из неё начального значения (initial value, seed), необходимого генераторам случайных чисел (ГСЧ) для формирования случайных чисел. ГПСЧ использует единственное начальное значение, откуда и следует его псевдослучайность, а ГСЧ всегда формирует случайное число, имея в начале высококачественную случайную величину, предоставленную различными источниками энтропии.
Энтропия – это мера беспорядка. Информационная энтропия — мера неопределённости или непредсказуемости информации.
Можно сказать, что ГСЧ = ГПСЧ + источник энтропии.

Уязвимости ГПСЧ

Линейный конгруэнтный ГПСЧ (LCPRNG)

Распространённый метод для генерации псевдослучайных чисел, не обладающий криптографической стойкостью. Линейный конгруэнтный метод заключается в вычислении членов линейной рекуррентной последовательности по модулю некоторого натурального числа m, задаваемой следующей формулой:

где a (multiplier), c (addend), m (mask) — некоторые целочисленные коэффициенты. Получаемая последовательность зависит от выбора стартового числа (seed) X0 и при разных его значениях получаются различные последовательности случайных чисел.

Для выбора коэффициентов имеются свойства позволяющие максимизировать длину периода(максимальная длина равна m), то есть момент, с которого генератор зациклится [1].

Пусть генератор выдал несколько случайных чисел X0, X1, X2, X3. Получается система уравнений

Решив эту систему, можно определить коэффициенты a, c, m. Как утверждает википедия [8], эта система имеет решение, но решить самостоятельно или найти решение не получилось. Буду очень признателен за любую помощь в этом направлении.

Предсказание результатов линейно-конгруэнтного метода

Основным алгоритмом предсказания чисел для линейно-конгруэнтного метода является Plumstead’s — алгоритм, реализацию, которого можно найти здесь [4](есть онлайн запуск) и здесь [5]. Описание алгоритма можно найти в [9].
Простая реализация конгруэнтного метода на Java.

Отправив 20 чисел на сайт [4], можно с большой вероятностью получить следующие. Чем больше чисел, тем больше вероятность.

Взлом встроенного генератора случайных чисел в Java

Многие языки программирования, например C(rand), C++(rand) и Java используют LСPRNG. Рассмотрим, как можно провести взлом на примере java.utils.Random. Зайдя в исходный код (jdk1.7) данного класса можно увидеть используемые константы

Метод java.utils.Randon.nextInt() выглядит следующим образом (здесь bits == 32)

Результатом является nextseed сдвинутый вправо на 48-32=16 бит. Данный метод называется truncated-bits, особенно неприятен при black-box, приходится добавлять ещё один цикл в brute-force. Взлом будет происходить методом грубой силы(brute-force).

Пусть мы знаем два подряд сгенерированных числа x1 и x2. Тогда необходимо перебрать 2^16 = 65536 вариантов oldseed и применять к x1 формулу:

до тех пор, пока она не станет равной x2. Код для brute-force может выглядеть так

Вывод данной программы будет примерно таким:

Несложно понять, что мы нашли не самый первый seed, а seed, используемый при генерации второго числа. Для нахождения первоначального seed необходимо провести несколько операций, которые Java использовала для преобразования seed, в обратном порядке.

И теперь в исходном коде заменим
crackingSeed.set(seed);
на
crackingSeed.set(getPreviousSeed(seed));

И всё, мы успешно взломали ГПСЧ в Java.

Взлом ГПСЧ Mersenne twister в PHP

Рассмотрим ещё один не криптостойкий алгоритм генерации псевдослучайных чисел Mersenne Twister. Основные преимущества алгоритма — это скорость генерации и огромный период 2^19937 − 1, На этот раз будем анализировать реализацию алгоритма mt_srand() и mt_rand() в исходном коде php версии 5.4.6.

Можно заметить, что php_mt_reload вызывается при инициализации и после вызова php_mt_rand 624 раза. Начнем взлом с конца, обратим трансформации в конце функции php_mt_rand(). Рассмотрим (s1 ^ (s1 >> 18)). В бинарном представление операция выглядит так:

10110111010111100111111001110010 s1
00000000000000000010110111010111100111111001110010 s1 >> 18
10110111010111100101001110100101 s1 ^ (s1 >> 18)
Видно, что первые 18 бит (выделены жирным) остались без изменений.
Напишем две функции для инвертирования битового сдвига и xor

Тогда код для инвертирования последних строк функции php_mt_rand() будет выглядеть так

Если у нас есть 624 последовательных числа сгенерированных Mersenne Twister, то применив этот алгоритм для этих последовательных чисел, мы получим полное состояние Mersenne Twister, и сможем легко определить каждое последующее значение, запустив php_mt_reload для известного набора значений.

Область для взлома

Если вы думаете, что уже нечего ломать, то Вы глубоко заблуждаетесь. Одним из интересных направлений является генератор случайных чисел Adobe Flash(Action Script 3.0). Его особенностью является закрытость исходного кода и отсутствие задания seed’а. Основной интерес к нему, это использование во многих онлайн-казино и онлайн-покере.
Есть много последовательностей чисел, начиная от курса доллара и заканчивая количеством времени проведенным в пробке каждый день. И найти закономерность в таких данных очень не простая задача.

Задание распределения для генератора псевдослучайных чисел

Для любой случайной величины можно задать распределение. Перенося на пример с картами, можно сделать так, чтобы тузы выпадали чаще, чем девятки. Далее представлены несколько примеров для треугольного распределения и экспоненциального распределения.

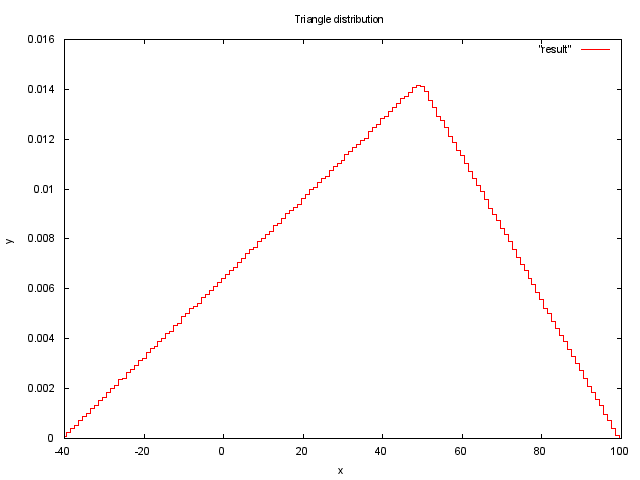
Треугольное распределение

Приведем пример генерации случайной величины с треугольным распределением [7] на языке C99.

Экспоненциальное распределение

Тесты ГПСЧ

Некоторые разработчики считают, что если они скроют используемый ими метод генерации или придумают свой, то этого достаточно для защиты. Это очень распространённое заблуждение. Следует помнить, что есть специальные методы и приемы для поиска зависимостей в последовательности чисел.

Одним из известных тестов является тест на следующий бит — тест, служащий для проверки генераторов псевдослучайных чисел на криптостойкость. Тест гласит, что не должно существовать полиномиального алгоритма, который, зная первые k битов случайной последовательности, сможет предсказать k+1 бит с вероятностью большей ½.

В теории криптографии отдельной проблемой является определение того, насколько последовательность чисел или бит, сгенерированных генератором, является случайной. Как правило, для этой цели используются различные статистические тесты, такие как DIEHARD или NIST. Эндрю Яо в 1982 году доказал, что генератор, прошедший «тест на следующий бит», пройдет и любые другие статистические тесты на случайность, выполнимые за полиномиальное время.
В интернете [10] можно пройти тесты DIEHARD и множество других, чтобы определить критостойкость алгоритма.

Как выбрать случайное число от 1 до 10

Представьте, что вам нужно сгенерировать равномерно распределённое случайное число от 1 до 10. То есть целое число от 1 до 10 включительно, с равной вероятностью (10%) появления каждого. Но, скажем, без доступа к монетам, компьютерам, радиоактивному материалу или другим подобным источникам (псевдо) случайных чисел. У вас есть только комната с людьми.

Предположим, что в этой комнате чуть более 8500 студентов.

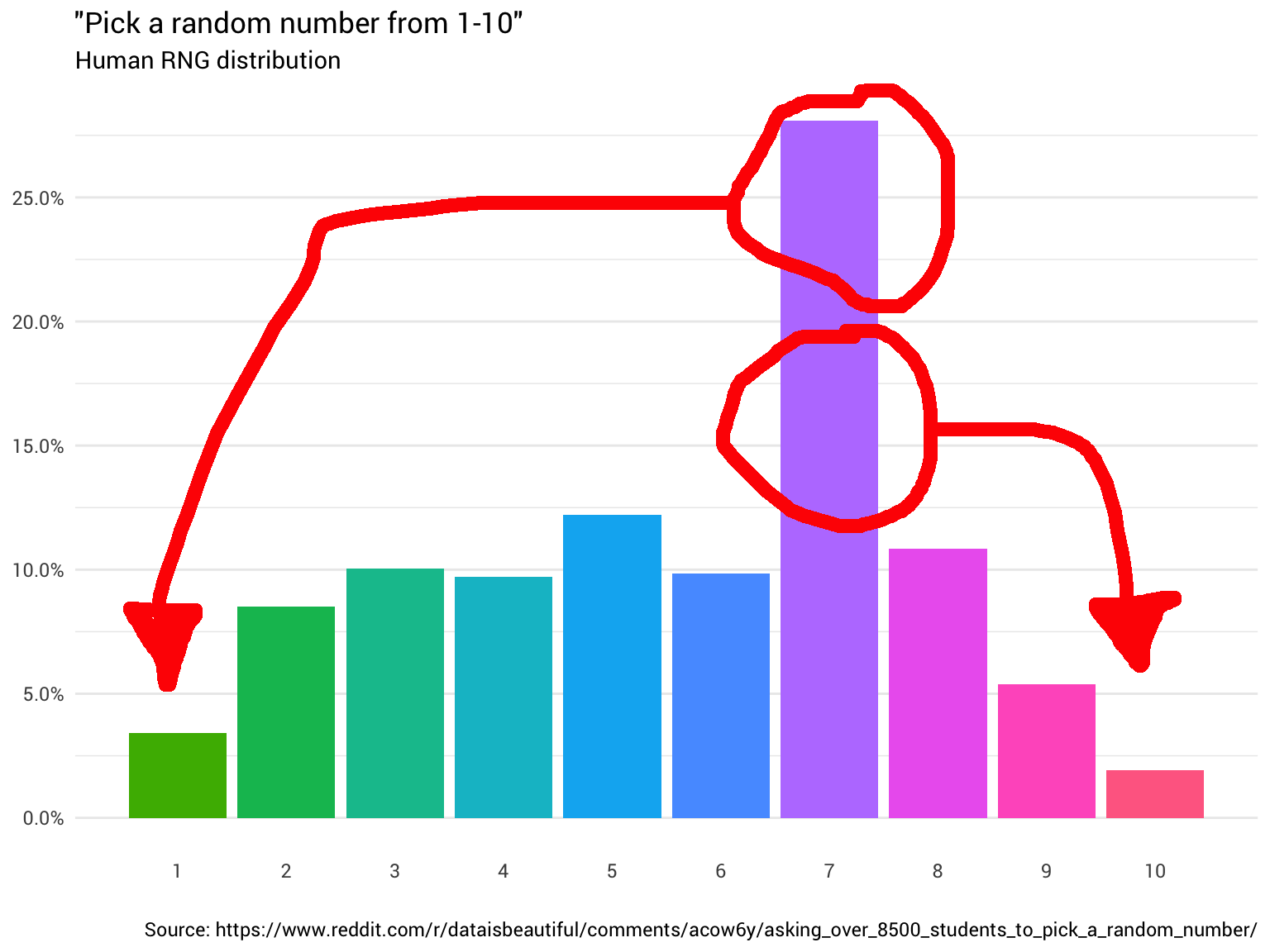
Самое простое — попросить кого-нибудь: «Эй, выбери случайное число от одного до десяти!». Человек отвечает: «Семь!». Отлично! Теперь у вас есть число. Однако вы начинаете задаваться вопросом, является ли оно равномерно распределённым?

Поэтому вы решили спросить ещё несколько человек. Вы продолжаете их спрашивать и считать их ответы, округляя дробные числа и игнорируя тех, кто думает, что диапазон от 1 до 10 включает 0. В конце концов вы начинаете видеть, что распределение вообще не равномерное:

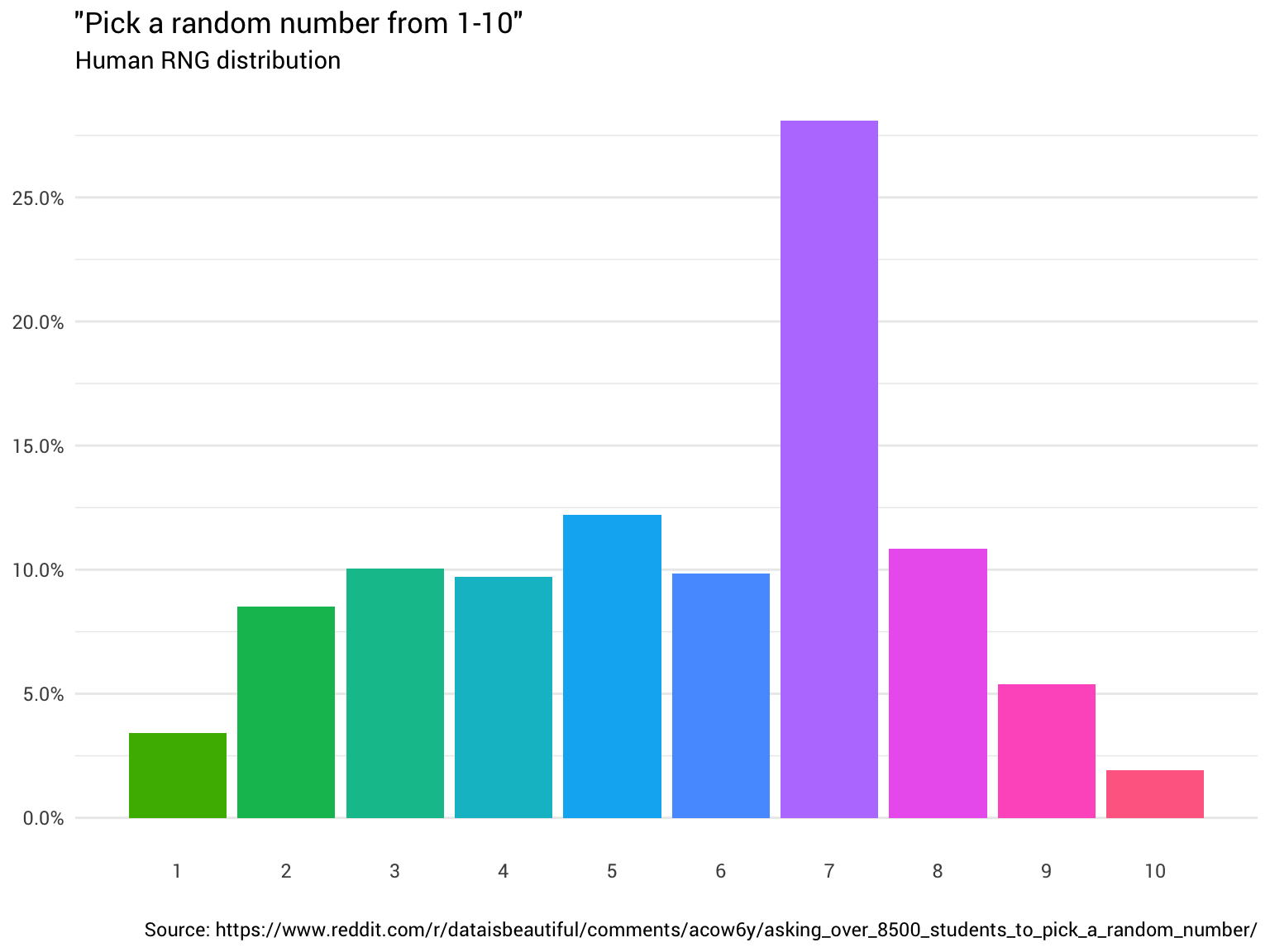
Данные с Reddit

Вы хлопаете себя по лбу. Ну конечно, оно не будет случайным. В конце концов, нельзя доверять людям.

Итак, что делать?

Вот бы найти какую-то функцию, которая преобразует распределение «человеческого ГСЧ» в равномерное распределение…

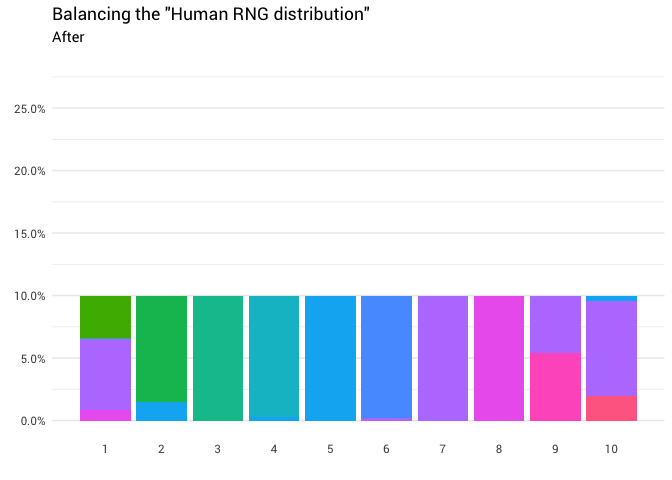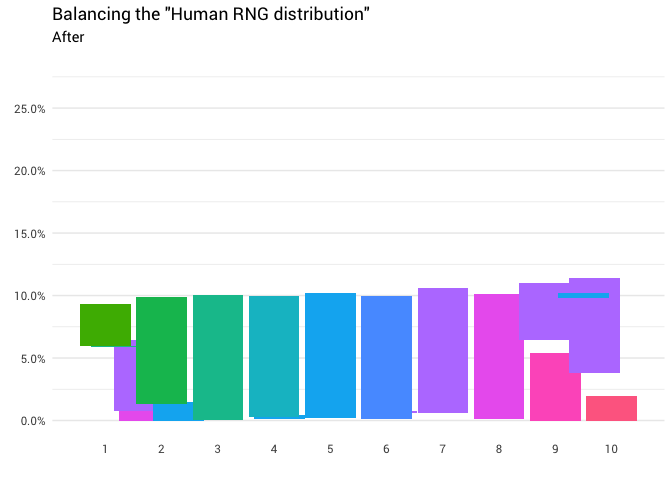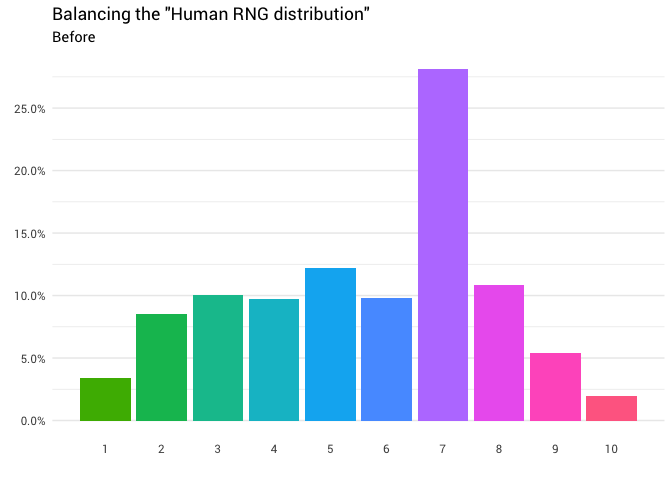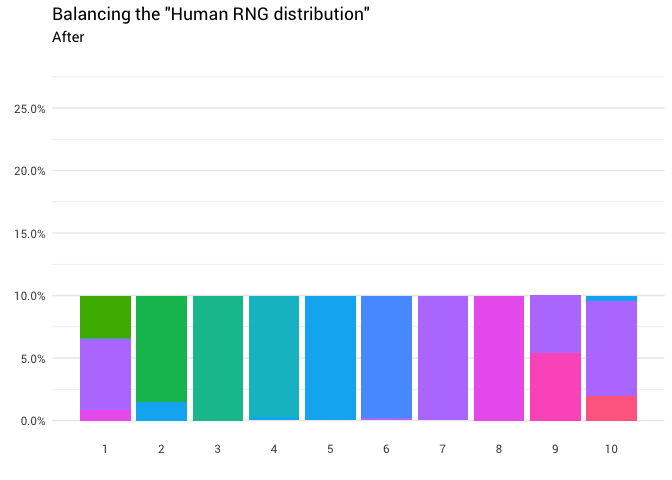
Интуиция тут относительно проста. Нужно всего лишь взять массу распределения оттуда, где она выше 10%, и переместить туда, где она меньше 10%. Так, чтобы все столбцы на графике были одного уровня:

По идее, такая функция должна существовать. Фактически, должно быть много различных функций (для перестановки). В крайнем случае, можно «разрезать» каждый столбец на бесконечно малые блоки и построить распределение любой формы (как кирпичики Lego).

Конечно, такой экстремальный пример немного громоздок. В идеале мы хотим сохранить как можно больше исходного распределения (т. е. сделать как можно меньше измельчений и перемещений).

Как найти такую функцию?

Ну, наше объяснение выше звучит очень похоже на линейное программирование. Из Википедии:

Линейное программирование (LP, также именуется линейной оптимизацией) — метод достижения наилучшего результата… в математической модели, требования которой представлены линейными отношениями… Стандартная форма представляет собой обычную и наиболее интуитивную форму описания задачи линейного программирования. Она состоит из трёх частей:

Представление проблемы

У нас есть набор переменных , каждая из которых кодирует долю вероятности, перераспределённую от целого числа (от 1 до 10) к целому числу (от 1 до 10). Поэтому, если , то нам нужно перенести 20% ответов от семёрки к единице.

Мы хотим ограничить эти переменные таким образом, чтобы все перераспределённые вероятности суммировались в 10%. Другими словами, для каждого от 1 до 10:

Можем представить эти ограничения в виде списка массивов в R. Позже свяжем их в матрицу.

Мы также должны убедиться, что сохраняется вся масса вероятностей из исходного распределения. Так что для каждого в диапазоне от 1 до 10:

Как уже говорилось, мы хотим максимизировать сохранение исходного распределения. Это наша цель (objective):

Затем передаём проблему солверу, например, пакету lpSolve в R, объединив созданные ограничения в одну матрицу:

Возвращается следующее перераспределение:

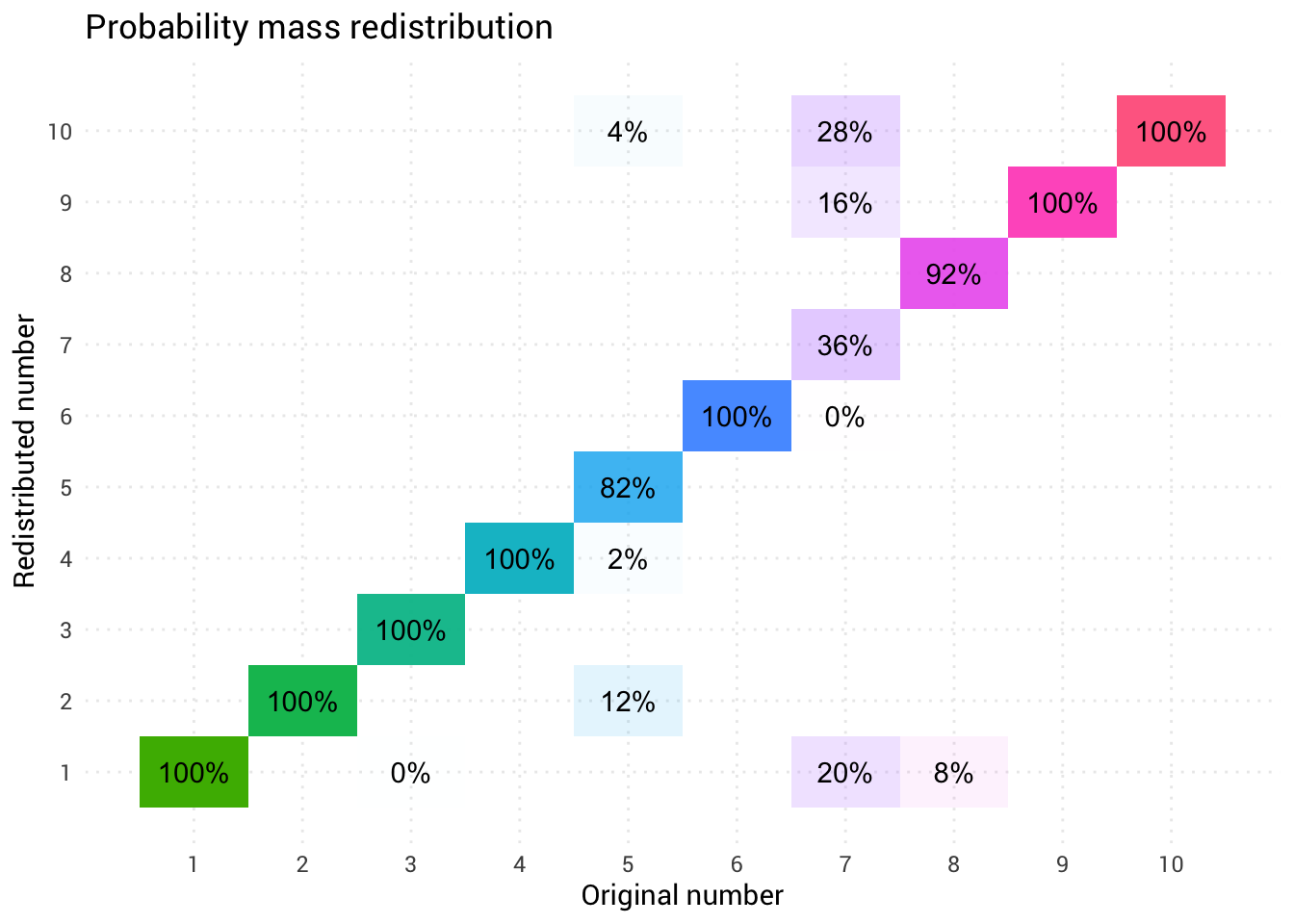
Отлично! Теперь у нас есть функция перераспределения. Давайте поближе посмотрим, как именно движется масса:

Эта диаграмма говорит, что примерно в 8% случаев, когда кто-то называет восемь в качестве случайного числа, вам нужно воспринимать ответ как единицу. В остальных 92% случаев он остаётся восьмёркой.

Было бы довольно просто решить задачу, если бы у нас был доступ к генератору равномерно распределённых случайных чисел (от 0 до 1). Но у нас только комната, полная людей. К счастью, если вы готовы примириться с несколькими небольшими неточностями, то из людей можно сделать довольно хороший ГСЧ, не спрашивая более двух раз.

Возвращаясь к нашему исходному распределению, у нас есть следующие вероятности для каждого числа, которые можно использовать для повторного назначения любой вероятности, если необходимо.

Например, когда кто-то даёт нам восемь в качестве случайного числа, нужно определить, должна ли эта восьмёрка стать единицей или нет (вероятность 8%). Если мы спросим другого человека о случайном числе, то с вероятностью 8,5% он ответит «два». Так что если это второе число равно 2, мы знаем, что должны вернуть 1 как равномерно распределённое случайное число.

Распространив эту логику на все числа, получаем следующий алгоритм:

Генератор случайных чисел в Excel

В данной статье мы рассмотрим особенности алгоритма генератора случайных чисел в Excel, и на примерах рассмотрим, как использовать функции СЛЧИС и СЛУЧМЕЖДУ в Excel для генерации случайных чисел, случайных чисел с заданным количеством знаков после запятой, дат и времени.

Генератор случайных чисел с использованием функции СЛЧИС

Функция СЛЧИС является одной из двух функций, специально предназначенных для генерации случайных чисел в Excel. Данная функция возвращает случайное десятичное число (действительное число) между 0 и 1.

СЛЧИС() является энергозависимой функцией, что означает, что при каждом вычислении рабочего листа создается новое случайное число. И это происходит каждый раз, когда вы выполняете какое-либо действие на листе, например, обновляете формулу (не обязательно формулу СЛЧИС, любую другую формулу на листе), редактируете ячейку или вводите новые данные.

Функция СЛЧИС доступна во всех версиях: Excel 2016, Excel 2013, Excel 2010, Excel 2007, Excel 2003.

Поскольку функция Excel СЛЧИС не имеет аргументов, вы просто вводите =СЛЧИС() в ячейке и затем копируете формулу на столько ячеек, сколько хотите:

Генератор случайных чисел в Excel – Генерация случайных чисел

А теперь давайте сделаем еще один шаг и напишем несколько формул СЛЧИС для генерации случайных чисел в соответствии с определенными условиями.

Генератор случайных чисел от нуля до заданной верхней границы диапазона

Чтобы сделать генератор случайных чисел от нуля до любого значения N, вы несколько раз выполняете функцию СЛЧИС с помощью N:

Например, для создания последовательности случайных чисел, больших или равных 0, но менее 50, используйте следующую формулу:

Генератор случайных чисел в диапазоне

Чтобы создать случайное число в диапазоне, т.е. случайное число между любыми двумя указанными вами числами, используйте следующую формулу СЛЧИС:

Где A – это нижнее значение границы (наименьшее число), а B – верхнее значение границы (наибольшее число).

Например, чтобы сделать генератор случайных чисел от 10 до 50, вы можете использовать следующую формулу:

Генератор случайных целых чисел в Excel

Чтобы сделать генератор случайных целых чисел от 0 до 50:

Чтобы генерировать случайные целые числа от 10 до 50:

Генератор случайных чисел в Excel – Генерация случайных целых чисел

Генератор случайных чисел в Excel в диапазоне с помощью функции СЛУЧМЕЖДУ

СЛУЧМЕЖДУ – это еще одна функция в Excel для создания генератора случайных чисел.. Она возвращает случайные целые числа в указанном диапазоне:

СЛУЧМЕЖДУ (нижняя граница; верхняя граница)

Очевидно, что нижняя граница – это наименьшее число, а верхняя граница – наибольшее число в диапазоне случайных чисел, которые вы хотите получить.

Подобно СЛЧИС, СЛУЧМЕЖДУ в Excel является изменчивой функцией, и она также возвращает новое случайное целое число каждый раз, когда ваша таблица пересчитывается или изменяется.

Например, того чтобы сделать генератор случайных целых чисел от 10 до 50 (включая 10 и 50) используйте следующую формулу СЛУЧМЕЖДУ:

Генератор случайных чисел в Excel – Генерация случайных чисел в заданном диапазоне

Функция СЛУЧМЕЖДУ доступна в следующих версиях: Excel 2016, Excel 2013, Excel 2010 и Excel 2007.

Далее в этой статье вы найдете еще несколько примеров формул, демонстрирующих, как использовать функцию СЛУЧМЕЖДУ для создания генератора случайных чисел, отличных от целых.

Создание случайных чисел с заданным количеством знаков после запятой

Хотя функция СЛУЧМЕЖДУ в Excel была предназначена для генерации случайных целых чисел, вы можете использовать ее для генерации случайных десятичных чисел с таким количеством десятичных знаков, сколько хотите.

Например, чтобы получить список чисел с одним десятичным знаком, вы умножаете нижнее и верхнее значения на 10, а затем делите возвращаемое значение на 10:

= СЛУЧМЕЖДУ(нижняя граница*10; верхняя граница*10)/10

Например, чтобы получить список чисел с одним десятичным знаком, вы умножаете нижнее и верхнее значения на 10, а затем делите возвращаемое значение на 10:

Следующая формула СЛУЧМЕЖДУ возвращает случайные десятичные числа от 1 до 50:

Генератор случайных чисел в Excel – Генерация случайных чисел с одним знаком после запятой

Аналогичным образом, чтобы сделать генератор случайных чисел от 1 до 50 с двумя знаками после запятой, вы умножаете аргументы функции СЛУЧМЕЖДУ на 100, а затем делите результат на 100:

Генератор случайных чисел в Excel – Генерация случайных чисел с двумя знаками после запятой

Генератор случайных дат в Excel

Чтобы вернуть список случайных дат между данными двумя датами, используйте функцию СЛУЧМЕЖДУ в сочетании с ДАТА:

=СЛУЧМЕЖДУ (ДАТА (дата начала); ДАТА (дата окончания))

Например, чтобы получить список дат между 1 сентября 2017 и 20 ноября 2017 включительно, введите следующую формулу на листе:

Не забудьте применить формат даты к ячейке (ячейкам), и вы получите список случайных дат, подобных этому:

Генератор случайных чисел в Excel – Генерация случайных дат

Генератор случайного времени в Excel

Во внутренней системе Excel времена хранятся как десятичные числа, и вы можете использовать стандартную функцию Excel СЛЧИС для вставки случайных действительных чисел, а затем просто применить формат времени к ячейкам:

Генератор случайных чисел в Excel – Генерация случайного времени функцией СЛЧИС и применение к ней формата Время

Чтобы сделать генератор случайного времени в указанном диапазоне, требуется более конкретная формула. Рассмотрим подробнее.

Генератор случайного времени в указанном диапазоне

Чтобы вставить произвольное время между любыми двумя указанными вами временными интервалами, используйте функцию ВРЕМЯ в сочетании с Excel СЛЧИС:

Например, чтобы вставить случайное время между 5:30 и 18:00, вы можете использовать одну из следующих формул:

Генератор случайных чисел в Excel – Генерация случайного времени в заданном интервале

Генератор случайных букв в Excel

Чтобы вставить случайную букву, необходимо использовать комбинацию трех различных функций:

Разберем функции, в приведенной выше формуле:

Генератор случайных чисел в Excel – Генерация случайных букв

Так как коды ANSI отличаются для прописных и строчных букв, эта формула учитывает регистр.

Если кто-то наизусть знает Коды символов ANSI, ничто не мешает вам передавать коды непосредственно в функцию СЛУЧМЕЖДУ.

Например, чтобы получить произвольные прописные буквы между A (код ANSI 65) и Z (код ANSI 90), вы пишете:

Чтобы генерировать строчные буквы между а (код ANSI 97) в z (код ANSI 122), вы используете следующую формулу:

Генератор случайных чисел в Excel – Генерация случайных символов

Как предотвратить повторное вычисление СЛЧИС и СЛУЧМЕЖДУ

Если вы хотите получить постоянный набор случайных чисел, дат или текстовых строк, которые не будут меняться каждый раз, то есть зафиксировать случайные числа, когда лист пересчитывается, используйте один из следующих способов:

Генератор случайных чисел в Excel – Вставка значений

Генератор случайных чисел с помощью Анализа данных

С помощью пакета анализа данных вы, например, можете сгенерировать случайные числа нормального распределения или другого распределения. По умолчанию данный пакет не подключен, поэтому необходимо его загрузить. Как это сделать, описано в этой статье.

Пример генерации случайных чисел нормального распределения

Для того чтобы сгенерировать случайные числа нормального распределения, переходим во вкладку « ДАННЫЕ », в группе « Анализ » выбираем « Анализ данных ».

Генератор случайных чисел в Excel – Анализ данных

В открывшемся списке выбираем «Генерация случайных чисел» и нажимаем кнопку « ОК ».

Генератор случайных чисел в Excel – Генерация случайных чисел

В открывшемся окне в списке «Распределение» выбираем «Нормальное», вводим число переменных, число случайных чисел, среднее и отклонение, а также место, где вы хотите разместить сгенерированные случайные числа.

Генератор случайных чисел в Excel – Генерация случайных чисел нормального распределения

После того, как все данные введены нажимаем кнопку « ОК », и в результате получаем сгенерированные случайные числа нормального распределения.

Ну вот на этом все. Теперь вы научились, как сделать генератор случайных чисел, чисел в диапазоне, чисел с заданным количеством знаков после запятой, случайных дат, случайного времени, а также случайных букв, а также, как сгенерировать случайные числа нормального распределения. Таким образом, владея данными знаниями, вы можете создать не только генератор случайных чисел в Excel, но и генератор паролей.

Краеугольный камень псевдослучайности: с чего начинается поиск чисел

(с)

Случайные числа постоянно генерируются каждой машиной, которая может обмениваться данными. И даже если она не обменивается данными, каждый компьютер нуждается в случайности для распределения программ в памяти. При этом, конечно, компьютер, как детерминированная система, не может создавать истинные случайные числа.

Когда речь заходит о генераторах случайных (или псевдослучайных) чисел, рассказ всегда строится вокруг поиска истинной случайности. Пока серьезные математики десятилетиями ведут дискуссии о том, что считать случайностью, в практическом отношении мы давно научились использовать «правильную» энтропию. Впрочем, «шум» — это лишь вершина айсберга.

С чего начать, если мы хотим распутать клубок самых сильных алгоритмов PRNG и TRNG? На самом деле, с какими бы алгоритмами вы не имели дело, все сводится к трем китам: seed, таблица предопределенных констант и математические формулы.

Каким бы ни был seed, еще есть алгоритмы, участвующие в генераторах истинных случайных чисел, и такие алгоритмы никогда не бывают случайными.

Что такое случайность

Первое подходящее определение случайной последовательности дал в 1966 году шведский статистик Пер Мартин-Лёф, ученик одного из крупнейших математиков XX века Андрея Колмогорова. Ранее исследователи пытались определить случайную последовательность как последовательность, которая проходила все тесты на случайность.

Основная идея Мартина-Лёфа заключалась в том, чтобы использовать теорию вычислимости для формального определения понятия теста случайности. Это контрастирует с идеей случайности в вероятности; в этой теории ни один конкретный элемент пространства выборки не может быть назван случайным.

«Случайная последовательность» в представлениях Мартина-Лёфа должна быть типичной, т.е. не должна обладать индивидуальными отличительными особенностями.

Было показано, что случайность Мартина-Лёфа допускает много эквивалентных характеристик, каждая из которых удовлетворяет нашему интуитивному представлению о свойствах, которые должны иметь случайные последовательности:

Существование множественных определений рандомизации Мартина-Лёфа и устойчивость этих определений при разных моделях вычислений свидетельствуют о том, что случайность Мартина-Лёфа является фундаментальным свойством математики.

Seed: основа псевдослучайных алгоритмов

Первые алгоритмы формирования случайных чисел выполняли ряд основных арифметических действий: умножить, разделить, добавить, вычесть, взять средние числа и т.д. Сегодня такие мощные алгоритмы, как Fortuna и Yarrow (используется в FreeBSD, AIX, Mac OS X, NetBSD) выглядят как генераторы случайных чисел для параноиков. Fortuna, например, это криптографический генератор, в котором для защиты от дискредитации после выполнения каждого запроса на случайные данные в размере 220 байт генерируются еще 256 бит псевдослучайных данных и используются в качестве нового ключа шифрования — старый ключ при этом каждый раз уничтожается.

Прошли годы, прежде чем простейшие алгоритмы эволюционировали до криптографически стойких генераторов псевдослучайных чисел. Частично этот процесс можно проследить на примере работы одной математической функции в языке С.

Функция rand () является простейшей из функций генерации случайных чисел в C.

В этом примере рандома используется вложенный цикл для отображения 100 случайных значений. Функция rand () хороша при создании множества случайных значений, но они являются предсказуемыми. Чтобы сделать вывод менее предсказуемым, вам нужно добавить seed в генератор случайных чисел — это делается с помощью функции srand ().

Seed — это стартовое число, точка, с которой начинается последовательность псевдослучайных чисел. Генератор псевдослучайных чисел использует единственное начальное значение, откуда и следует его псевдослучайность. Генератор истинных случайных чисел всегда имеет в начале высококачественную случайную величину, предоставленную различными источниками энтропии.

srand() принимает число и ставит его в качестве отправной точки. Если seed не выставить, то при каждом запуске программы мы будем получать одинаковые случайные числа.

Вот пример простой формулы случайного числа из «классики» — книги «Язык программирования C» Кернигана и Ричи, первое издание которой вышло аж в 1978 году:

Эта формула предполагает существование переменной, называемой random_seed, изначально заданной некоторым числом. Переменная random_seed умножается на 1 103 535 245, а затем 12 345 добавляется к результату; random_seed затем заменяется этим новым значением. Это на самом деле довольно хороший генератор псевдослучайных чисел. Если вы используете его для создания случайных чисел от 0 до 9, то первые 20 значений, которые он вернет при seed = 10, будут такими:

Если у вас есть 10 000 значений от 0 до 9, то распределение будет следующим:

0 — 10151 — 10242 — 10483 — 9964 — 9885 — 10016 — 9967 — 10068 — 9659 — 961

Любая формула псевдослучайных чисел зависит от начального значения. Если вы предоставите функции rand() seed 10 на одном компьютере, и посмотрите на поток чисел, которые она производит, то результат будет идентичен «случайной последовательности», созданной на любом другом компьютере с seed 10.

К сожалению, у генератора случайных чисел есть и другая слабость: вы всегда можете предсказать, что будет дальше, основываясь на том, что было раньше. Чтобы получить следующее число в последовательности, мы должны всегда помнить последнее внутреннее состояние генератора — так называемый state. Без state мы будем снова делать одну и ту же математическую операцию с одинаковыми числами, чтобы получить тот же ответ.

Как сделать seed уникальным для каждого случая? Самое очевидное решение — добавить в вычисления текущее системное время. Сделать это можно с помощью функции time().

Функция time() возвращает информацию о текущем времени суток, значение, которое постоянно изменяется. При этом метод typecasting гарантирует, что значение, возвращаемое функцией time(), является целым числом.

Итак, в результате добавления «случайного» системного времени функция rand() генерирует значения, которые являются более случайными, чем мы получили в первом примере.

Однако в этом случае seed можно угадать, зная системное время или время запуска приложения. Как правило, для приложений, где случайные числа являются абсолютно критичными, лучше всего найти альтернативное решение.

Но опять же, все эти числа не случайны.

Лучшее, что вы можете сделать с детерминированными генераторами псевдослучайных чисел — добавить энтропию физических явлений.

Период (цикл) генератора

Одними из наиболее часто используемых методов генерации псевдослучайных чисел являются различные модификации линейного конгруэнтного метода, схема которого была предложена Дерриком Лемером еще в 1949 году:

Рассмотрим случай, когда seed равен 1, а период — 100 (на языке Haskell):

В результате мы получим следующий ответ:

Это лишь пример и подобную структуру в реальной жизни не используют. В Haskell, если вы хотите построить случайную последовательность, можно воспользоваться следующим кодом:

Выбор случайного Int дает вам обратно Int и новый StdGen, который вы можете использовать для получения более псевдослучайных чисел. Многие языки программирования, включая Haskell, имеют генераторы случайных чисел, которые автоматически запоминают свое состояние (в Haskell это randomIO).

Чем больше величина периода, тем выше надежность создания хороших случайных значений, однако даже с миллиардами циклов крайне важно использовать надежный seed. Реальные генераторы случайных чисел обычно используют атмосферный шум (поставьте сюда любое физическое явление — от движения мыши пользователя до радиоактивного распада), но мы можем и схитрить программным методом, добавив в seed асинхронные потоки различного мусора, будь то длины интервалов между последними heartbeat потоками или временем ожидания mutual exclusion (а лучше добавить все вместе).

Истинная случайность бит

Итак, получив seed с примесью данных от реальных физических явлений (либо максимально усложнив жизнь будущему взломщику самым большим набором потоков программного мусора, который только сможем придумать), установив state для защиты от ошибки повтора значений и добавив криптографических алгоритмов (или сложных математических задач), мы получим некоторый набор данных, который будем считать случайной последовательностью. Что дальше?

Дальше мы возвращаемся к самому началу, к одному из фундаментальных требований — тестам.

Национальный институт стандартов и технологий США вложил в «Пакет статистических тестов для случайных и псевдослучайных генераторов чисел для криптографических приложений» 15 базовых проверок. Ими можно и ограничиться, но этот пакет вовсе не является «вершиной» проверки случайности.

Одни из самых строгих статистических тестов предложил профессор Джордж Марсалья из Университета штата Флорида. «Тесты diehard» включают 17 различных проверок, некоторые из них требуют очень длинных последовательностей: минимум 268 мегабайт.

Случайность можно проверить с помощью библиотеки TestU01, представленной Пьером Л’Экуйе и Ричардом Симардом из Монреальского университета, включающей классические тесты и некоторые оригинальные, а также посредством общедоступной библиотеки SPRNG.

Еще один полезный сервис для количественного измерения случайности.

Случайные числа не случайны

Как создать генератор случайных чисел на JS и предсказать Math.random()

Вы когда-нибудь задумывались, как работает Math.random()? Что такое случайное число и как оно получается? А представьте вопрос на собеседовании — напишите свой генератор случайных чисел в пару строк кода. И так, что же это такое, случайность и возможно ли ее предсказать.

Генератор псевдослучайных чисел и генератор случайных чисел

Для того, чтобы получить что-то случайное, нам нужен источник энтропии, источник некого хаоса из который мы будем использовать для генерации случайности.

Этот источник используется для накопления энтропии с последующим получением из неё начального значения (initial value, seed), которое необходимо генераторам случайных чисел (ГСЧ) для формирования случайных чисел.

Генератор ПсевдоСлучайных Чисел использует единственное начальное значение, откуда и следует его псевдослучайность, в то время как Генератор Случайных Чисел всегда формирует случайное число, имея в начале высококачественную случайную величину, которая берется из различных источников энтропии.

Энтропия — это мера беспорядка. Информационная энтропия — мера неопределённости или непредсказуемости информации.

Выходит, что чтобы создать псевдослучайную последовательность нам нужен алгоритм, который будет генерить некоторую последовательность на основании определенной формулы. Но такую последовательность можно будет предсказать. Тем не менее, давайте пофантазируем, как бы могли написать свой генератор случайных чисел, если бы у нас не было Math.random()

ГПСЧ имеет некоторый алгоритм, который можно воспроизвести.
ГСЧ — это получение чисел полностью из какого либо шума, возможность просчитать который стремится к нулю. При этом в ГСЧ есть определенные алгоритмы для выравнивания распределения.

Придумываем алгоритм ГПСЧ

Генератор псевдослучайных чисел (ГПСЧ, англ. pseudorandom number generator, PRNG) — алгоритм, порождающий последовательность чисел, элементы которой почти независимы друг от друга и подчиняются заданному распределению (обычно равномерному).

Мы можем взять последовательность каких-то чисел и брать от них модуль числа. Самый простой пример, который приходит в голову. Нам нужно подумать, какую последовательность взять и модуль от чего. Если просто в лоб от 0 до N и модуль 2, то получится генератор 1 и 0:

Эта функция генерит нам последовательность 01010101010101… и назвать ее даже псевдослучайной никак нельзя. Чтобы генератор был случайным, он должен проходить тест на следующий бит. Но у нас не стоит такой задачи. Тем не менее даже без всяких тестов мы можем предсказать следующую последовательность, значит такой алгоритм в лоб не подходит, но мы в нужном направлении.

А что если взять какую-то известную, но нелинейную последовательность, например число PI. А в качестве значения для модуля будем брать не 2, а что-то другое. Можно даже подумать на тему меняющегося значения модуля. Последовательность цифр в числе Pi считается случайной. Генератор может работать, используя числа Пи, начиная с какой-то неизвестной точки. Пример такого алгоритма, с последовательностью на базе PI и с изменяемым модулем:

Но в JS число PI можно вывести только до 48 знака и не более. Поэтому предсказать такую последовательность все так же легко и каждый запуск такого генератора будет выдавать всегда одни и те же числа. Но наш генератор уже стал показывать числа от 0 до 9. Кстати, так выглядит распределение по выпадению чисел при 10000 итерациях:

Распределение очень неравномерное, но мы получим генератор чисел от 0 до 9.

Мы можем взять не число Pi, а время в числовом представлении и это число рассматривать как последовательность цифр, причем для того, чтобы каждый раз последовательность не повторялась, мы будем считывать ее с конца. Итого наш алгоритм нашего ГПСЧ будет выглядеть так:

Вот это уже похоже на генератор псевдослучайных чисел. И тот же Math.random() — это ГПСЧ, про него мы поговорим чуть позже. При этом у нас каждый раз первое число получается разным.

Собственно на этих простых примерах можно понять как работают более сложные генераторы случайных числе. И есть даже готовые алгоритмы. Для примера разберем один из них — это Линейный конгруэнтный ГПСЧ(LCPRNG).

Линейный конгруэнтный ГПСЧ

Линейный конгруэнтный ГПСЧ(LCPRNG) — это распространённый метод для генерации псевдослучайных чисел. Он не обладает криптографической стойкостью. Этот метод заключается в вычислении членов линейной рекуррентной последовательности по модулю некоторого натурального числа m, задаваемой следующей формулой:

где a(multiplier), c(addend), m(mask) — некоторые целочисленные коэффициенты. Получаемая последовательность зависит от выбора стартового числа — т.е. seed. При разных значениях seed получаются различные последовательности случайных чисел. Пример реализации такого алгоритма на JavaScript:

Многие языки программирования используют LСPRNG (но не именно такой алгоритм(!)).

Как говорилось выше, такую последовательность можно предсказать. Так зачем нам ГПСЧ? Если говорить про безопасность, то ГПСЧ — это проблема. Если говорить про другие задачи, то эти свойства — могут сыграть в плюс. Например для различных спец эффектов и анимаций графики может понадобиться частый вызов random. И вот тут важны распределение значений и перформанс! Секурные алгоритмы не могут похвастать скоростью работы.

Еще одно свойство — воспроизводимость. Некоторые реализации позволяют задать seed, и это очень полезно, если последовательность должна повторяться. Воспроизведение нужно в тестах, например. И еще много других вещей существует, для которых не нужен безопасный ГСЧ.

Как устроен Math.random()

Как устроен алгоритм Math.random() — интересный вопрос. До недавнего времени, а именно до 49 Chrome использовался алгоритм MWC1616:

Именно этот алгоритм генерит нам последовательность псевдослучайных чисел в промежутке между 0 и 1.

Исправил ошибку в алгоритме MWC1616 (пропущенные скобки). Эта же ошибка повторяется и в статье https://v8project.blogspot.ru/2015/12/theres-mathrandom-and-then-theres.html

то видим, что должны быть скобки:

Предсказываем Math.random()

Чем это было чревато? Есть такой квест: https://alf.nu/ReturnTrue

Что нужно вписать вместо вопросов, чтобы функция вернула true? Кажется что это невозможно. Но, это возможно, если вы заглядывали в спеку и видели алгоритм ГПСЧ V8. Решение этой задачи в свое время мне показал Роман Дворнов:

Этот код работал в 70% случаев для Chrome

Видите эти равномерности на левом слайде? Изображение показывает проблему с распределением значений. На картинке слева видно, что значения местами сильно группируются, а местами выпадают большие фрагменты. Как следствие — числа можно предсказать.

Выходит что мы можем отреверсить Math.random() и предсказать, какое было загадано число на основе того, что получили в данный момент времени. Для этого получаем два значения через Math.random(). Затем вычисляем внутреннее состояние по этим значениям. Имея внутреннее состояние можем предсказывать следующие значения Math.random() при этом не меняя внутреннее состояние. Меняем код так так, чтобы вместо следующего возвращалось предыдущее значение. Собственно все это и описано в коде-решении для задачи random4. Но потом алгоритм изменили (подробности читайте в спеке). Его можно будет сломать, как только у нас в JS появится нормальная работа с 64 битными числами. Но это уже будет другая история.

Новый алгоритм выглядит так:

Сrypto Random Values

Пример генерации случайного числа:

Но, в отличие от ГПСЧ Math.random(), этот метод очень ресурсоемкий. Дело в том, что данный генератор использует системные вызовы в ОС, чтобы получить доступ к источникам энтропии (мак адрес, цпу, температуре, etc…).

Материалы про Math.random()

Больше про random в спецификации:

Хорошая статья про работу рандомайзера

Пример реализации предсказателя с Math.random()

Кстати, следить за обновлениями и прочими материалами от меня можно в телеграм канале: @prowebit

Written by Alexander Mayorov
Full Stack CTO

Разбор алгоритмов генерации псевдослучайных чисел

Я работаю программистом в игровой студии IT Territory, а с недавних пор перешел на направление экспериментальных проектов, где мы проверяем на прототипах различные геймплейные гипотезы. И работая над одним из прототипов мы столкнулись с задачей генерации случайных чисел. Я хотел бы поделиться с вами полученным опытом: расскажу о псевдогенераторах случайных чисел, об альтернативе в виде хеш-функции, покажу, как её можно оптимизировать, и опишу комбинированные подходы, которые мы применяли в проекте.

Случайными числами пользовались с самого зарождения математики. Сегодня их применяют во всевозможных научных изысканиях, при проверке математических теорем, в статистике и т.д. Также случайные числа широко используются в игровой индустрии для генерирования 3D-моделей, текстур и целых миров. Их применяют для создания вариативности поведения в играх и приложениях.

Есть разные способы получения случайных чисел. Самый простой и понятный — это словари: мы предварительно собираем и сохраняем набор чисел и по мере надобности берём их по очереди.

К первым техническим способам получения случайных чисел можно отнести различные генераторы с использованием энтропии. Это устройства, основанные на физических свойствах, например, емкости конденсатора, шуме радиоволн, длительности нажатия на кнопку и так далее. Хоть такие числа действительно будут случайными, у таких способов отсутствует важный критерий — повторяемость.

ERNIE 1 — аппаратный генератор случайных чисел, созданный в 1957 году

Сегодня мы с вами поговорим о генераторах псевдослучайных чисел — вычисляемых функциях. К ним предъявляются следующие требования:

Длинный период. Любой генератор рано или поздно начинает повторяться, и чем позже это случится, тем лучше, тем непредсказуемее будет результат.

Портируемость алгоритма на различные системы.

Скорость получения последовательности. Чем быстрее, тем лучше.

Повторяемость результата. Это очень важный показатель. От него зависят все компьютерные игры, которые используют генераторы миров и различные системы с аналогичной функциональностью. Воспроизводимость даёт нам общий контент для всех, то есть мы можем генерировать на отдельных клиентах одинаковое содержимое. Также мы можем генерировать контент на лету в зависимости от входных данных, например, от местоположения игрока в мире. Ещё повторяемость случайных чисел используется для сохранения конкретного контента в виде зерна. То есть мы можем держать у себя только какое-то число или массив чисел, на основе которых будут генерироваться нужные нам параметры для заранее отобранного контента.

Зерно

Зерно — это основа генерирования. Оно представляет собой число или вектор чисел, который мы отправляем при инициализации генератора.

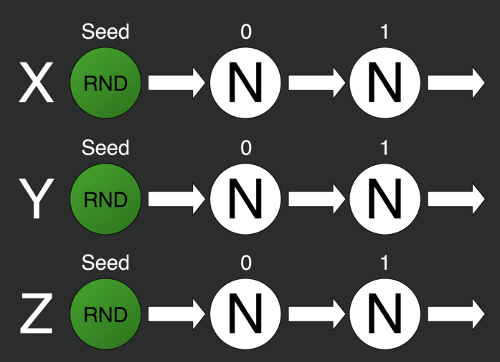
Решить эту проблему можно будет с помощью разделения одного генератора на несколько отдельных.

То есть берём несколько генераторов и задаём им разные зёрна. Но тут мы можем столкнуться со второй проблемой: нельзя гарантировать случайность i-тых элементов разных последовательностей с разными зёрнами.

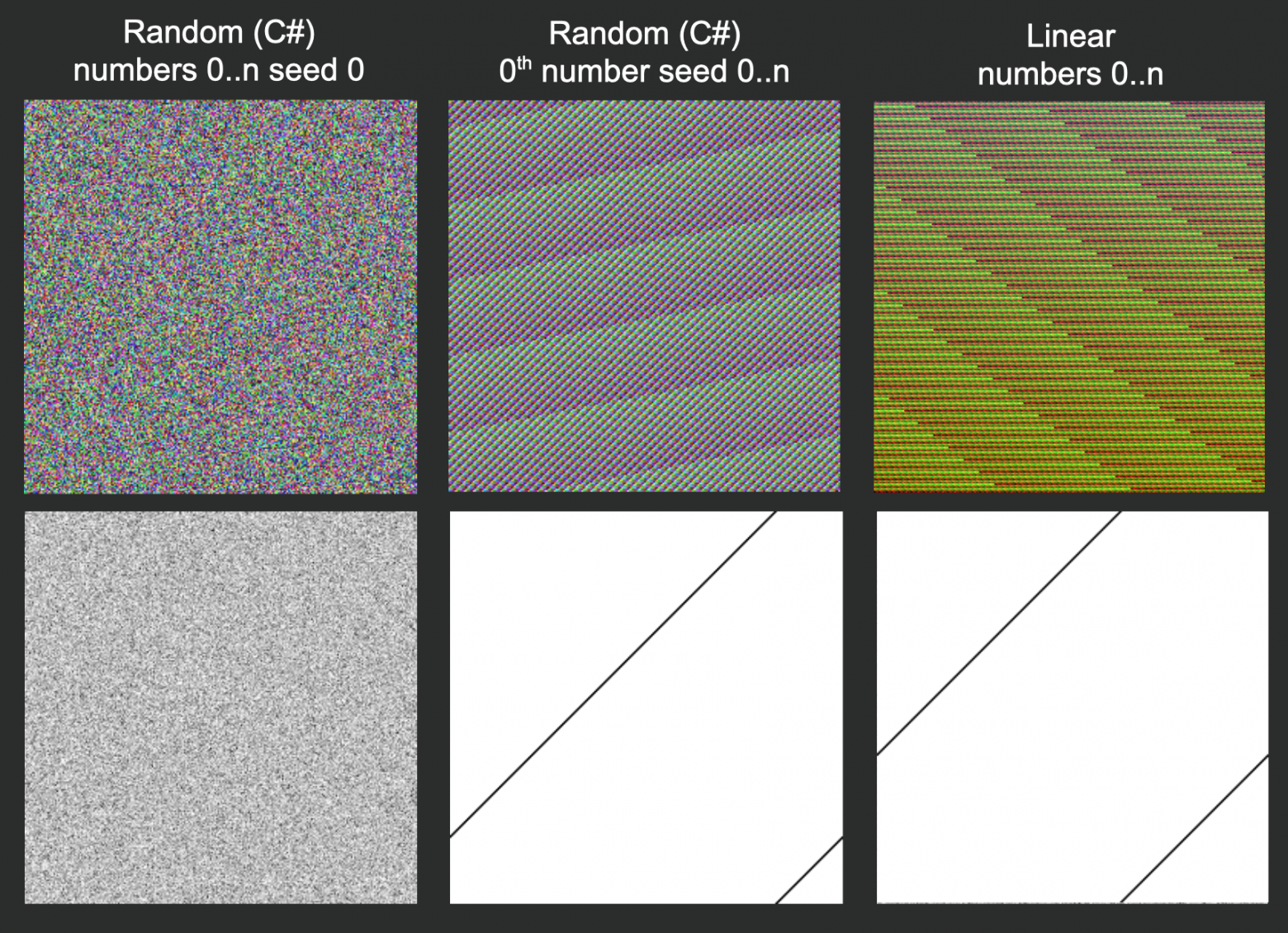
На иллюстрации изображён результат генерирования нулевого элемента последовательности с помощью стандартной библиотекой C#. Мы постепенно меняли зерно от 0 до N.

Качество генератора

Предлагаю оценивать качество генератора с помощью изображений разного типа. Первый тип — это просто сгенерированная последовательность, который мы визуализируем с помощью первых трёх байтов полученного числа, конвертированных в RGB-представление.

Второй тип изображений — это пространственная интерпретация сгенерированной последовательности. Мы берём первые два бита числа (Х и Y), затем считаем количество попаданий в заданные точки и при визуализации вычитаем из 1 отношение количества попаданий в конкретный пиксель к максимальному количеству попаданий в какой-то другой пиксель. Черные пиксели — это точка, куда мы попадаем чаще всего, а белые — куда мы либо почти, либо совсем не попали.

Сравнение генераторов

Стандартные средства C#

Ниже я сравнил стандартный генератор из библиотеки С# и линейную последовательность. Первый столбец слева — это случайная последовательность от 0 до N в рамках одного зерна. В центре вверху показаны нулевые элементы случайных последовательностей при разных зёрнах от 0 до N. Вторая линейная последовательность — это числа от 0 до N, которые я визуализировал нашим алгоритмом.

В рамках одного зерна генератор действительно создаёт случайное число. Но при этом для i-тых элементов последовательностей с разным зерном прослеживается паттерн, который схож с паттерном линейной последовательности.

Линейный конгруэнтный генератор (LCG)

Давайте рассмотрим другие алгоритмы. Деррик Генри в 1949 году создал линейный конгруэнтный генератор, который подбирает некие коэффициенты и с их помощью выполняет возведения в степень со сдвигом.

При генерировании с одним зерном паттерн нигде не образуется. Но при использовании i-тых элементов в последовательностях с различными зёрнами паттерн начинает прослеживаться. Причём его вид будет зависеть исключительно от коэффициентов, которые мы подобрали для генератора. Например, есть частный случай линейного конгруэнтного генератора — Randu.

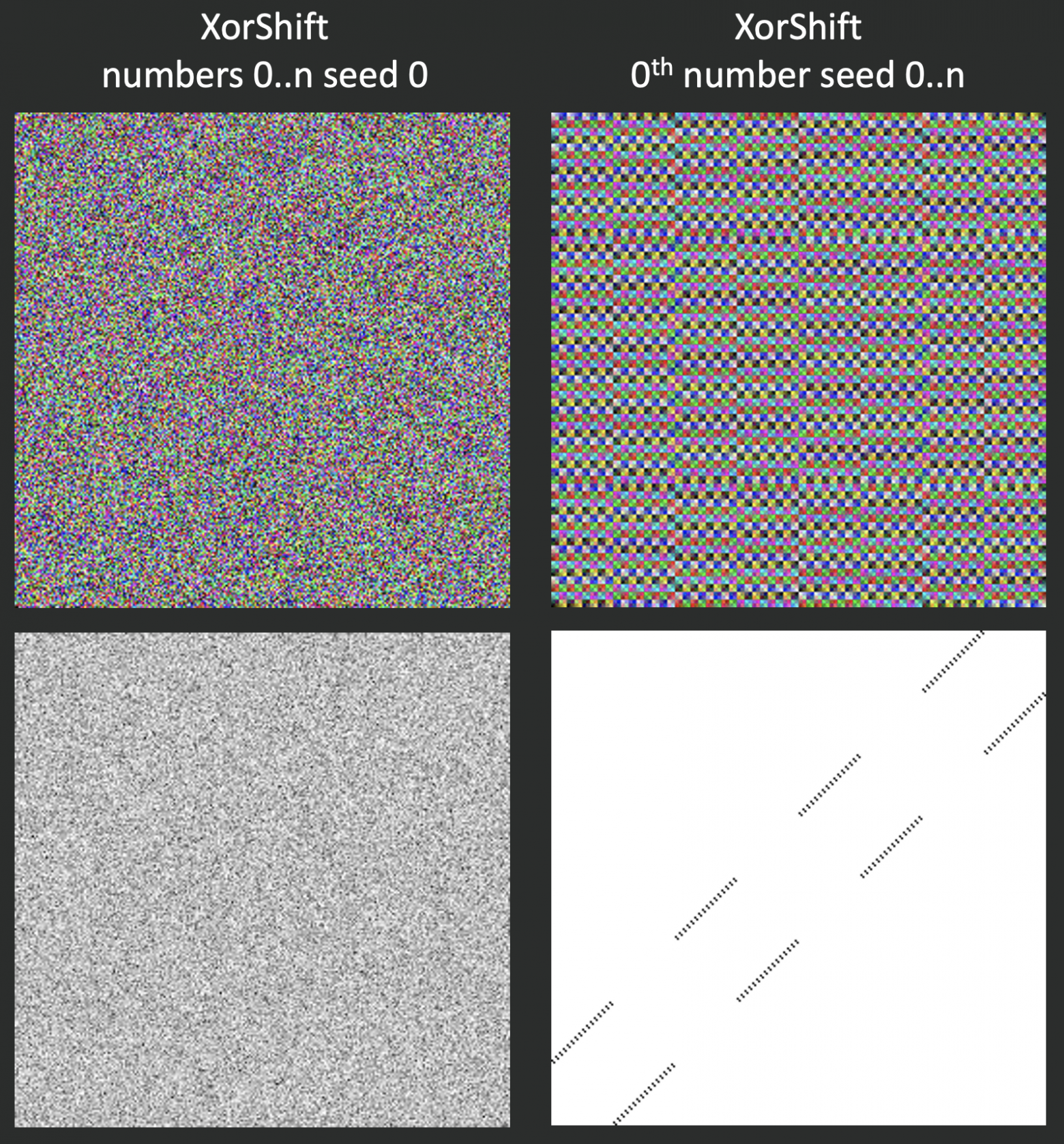
XorShift

Давайте теперь посмотрим на более свежую разработку — XorShift. Этот алгоритм просто выполняет операцию Xor и сдвигает байт в несколько раз. У него тоже будет прослеживаться паттерн для i-тых элементов последовательностей.

Вихрь Мерсенна

Неужели не существует генераторов без паттерна? Такой генератор есть — это вихрь Мерсенна. У этого алгоритма очень большой период, из-за чего появление паттерна на некотором количестве чисел физически невозможно. Однако и сложность этого алгоритма достаточно велика, в двух словах его не объяснить.

Unity — Random

Из других разработок стоит упомянуть генератор от компании Unity — Random, который используется в наборе стандартных библиотек для работы с Unity. При использовании первых элементов последовательности для разных зёрен у него будет прослеживаться паттерн, но при увеличении индекса паттерн исчезает и получается действительно случайная последовательность.

Перемешанный конгруэнтный генератор (PCG)

Противоположностью юнитёвского Random’a является перемешанный конгруэнтный генератор. Его особенность в том, что для первых элементов с различными зёрнами отсутствует ярко выраженный паттерн. Но при увеличении индекса он всё же возникает.

Длительность последовательного генерирования

Это важная характеристика генераторов. В таблице приведена длительность для алгоритмов в миллисекундах. Замеры проводились на моём MacBook Pro 2019 года.

0 seed 0..n

100 seed 0..n

Вихрь Мерсенна работает дольше всего, но даёт качественный результат. Стандартный генератор Random из библиотеки C# подходит для задач, в которых случайность вторична и не имеет какой-то значимой роли, то есть его можно использовать в рамках одного зерна. LCG (линейный конгруэнтный генератор) — это уже более серьёзный алгоритм, но требуется время на подбор нужных коэффициентов, чтобы получить адекватный паттерн. XorShift — самый быстрый алгоритм из всех рассмотренных. Его можно использовать там, где нужно быстро получить случайное значение, но помните про ярко выраженный паттерн с повторяющимся значением. Unity Random и PCG (перемешанный конгруэнтный генератор) сопоставимы по длительности работы, поэтому в разных ситуациях мы можем менять их местами: для длительных последовательностей использовать Unity, а для коротких — PCG.

Альтернатива генераторам — хеш-функции

Хеш-функции (функции свёртки) по определённому алгоритму преобразуют массив входных данных произвольной длины в строку заданной длины. Они позволяют быстрее искать данные, это свойство используется в хеш-таблицах. Также для хеш-функций характерна равномерность распределения, так называемый лавинный эффект. Это означает, что изменение малого количества битов во входном тексте приведёт к лавинообразному и сильному изменению значений выходного массива битов. То есть все выходные биты зависят от каждого входного бита.

Требования к генераторам на основе хеш-функций предъявляются те же самые, что и к простым генераторам, кроме длительности получения последовательности. Дело в том, что такому генератору можно отправить на вход одновременно зерно и требуемое состояние, потому что хеш-функции принимают на вход массивы данных.

Вот пример использования хеш-функции: можно либо создать конкретный класс, отправить туда зерно и постепенно запрашивать только конкретные состояния, либо написать статичную функцию, и отправить туда сразу и зерно, и конкретное состояние. Слева показан алгоритм работы MD5 из стандартной библиотеки C#.

Сделать генератор на основе хеш-функции можно так. Непосредственно при инициализации генератора задаём зерно, увеличиваем счётчик на 1 при запросе следующего значения и выводим результат хеша по зерну и счётчику.

Одни из самых популярных хеш-функций — это MurMur3 и WangHash.

MurMur3 не создаёт паттернов при использованиии i-тых элементов разных последовательностей при разных зёрнах. У WangHash статистические показатели образуют заметный паттерн. Но любую функцию можно прогнать через себя два раза и получить улучшенные показатели, как это показано в правом крайнем столбце WangDoubleHash.

Также сегодня активно развивается и набирает популярность алгоритм xxHash.

Забегая вперёд, скажу, что мы выбрали этот генератор для наших проектов и активно его используем.

Длительность последовательного генерирования у всех хеш-функций примерно одинакова. Однако у MD5 эта характеристика заметно отличается, но не потому, что алгоритм плохой, а потому что в стандартной реализации MD5 много разных состояний, которые влияют на быстродействие алгоритма.

9.5 – Генерирование случайных чисел

Возможность генерировать случайные числа может быть полезна в определенных видах программ, особенно в играх, программах статистического моделирования и научных симуляторах, которые должны моделировать случайные события. Возьмем, к примеру, игры – без случайных событий монстры всегда будут атаковать вас одинаково, вы всегда найдете одно и то же сокровище, расположение подземелий никогда не изменится и т.д. И это не сделает игру очень хорошей.

Так как же нам генерировать случайные числа? В реальной жизни мы часто получаем случайные результаты, например, подбрасывая монету, бросая кости или тасуя колоду карт. Эти события включают в себя так много физических переменных (например, гравитацию, трение, сопротивление воздуха, импульс и т.д.), что их почти невозможно предсказать или контролировать, и они дают результаты, которые во всех смыслах случайны.

Однако компьютеры не предназначены для использования преимуществ физических переменных – ваш компьютер не может подбрасывать монету, бросать кости или тасовать реальные карты. Компьютеры живут в управляемом электрическом мире, где всё двоично (ложь или истина) и нет промежуточного состояния. По самой своей природе компьютеры предназначены для получения максимально предсказуемых результатов. Когда вы говорите компьютеру вычислить 2 + 2, вы всегда хотите, чтобы ответ был 4. А не 3 или 5 в отдельных случаях.

Следовательно, компьютеры обычно не способны генерировать случайные числа. Вместо этого они должны моделировать случайность, что чаще всего делается с помощью генераторов псевдослучайных чисел.

Генератор псевдослучайных чисел (ГПСЧ или PRNG, pseudo-random number generator) – это программа, которая принимает начальное число (англ. seed) и выполняет над ним математические операции, чтобы преобразовать его в какое-то другое число, которое, кажется, не связано с начальным числом. Затем он берет это сгенерированное число и выполняет с ним ту же математическую операцию, чтобы преобразовать его в новое число, не связанное с числом, из которого оно было сгенерировано. Постоянно применяя алгоритм к последнему сгенерированному числу, он может генерировать последовательность новых чисел, которые будут казаться случайными, если алгоритм достаточно сложен.

Лучшая практика

Предоставить начальное значение своему генератору случайных чисел вы должны только один раз. Если ввести его более одного раза, результаты будут менее случайными или совсем не случайными.

На самом деле написать ГПСЧ довольно просто. Вот короткая программа, которая генерирует 100 псевдослучайных чисел:

Результат этой программы:

Каждое число кажется довольно случайным по сравнению с предыдущим. Как оказалось, наш алгоритм на самом деле не очень хорош по причинам, которые мы обсудим позже. Но он эффективно иллюстрирует принцип генерации значений генератором псевдослучайных чисел.

Генерация случайных чисел в C++

C (и, как следствие, C++) поставляется со встроенным генератором псевдослучайных чисел. Он реализован как две отдельные функции, которые находятся в заголовке cstdlib :

Вот пример программы, использующей эти функции:

Вот результат этой программы:

Последовательности ГПСЧ и заполнение

Если вы запустите приведенный выше пример программы с std::rand() несколько раз, вы заметите, что она каждый раз выводит один и тот же результат! Это означает, что хотя каждое число в последовательности кажется случайным по сравнению с предыдущими, вся последовательность вовсе не случайна! А это означает, что наша программа оказывается полностью предсказуемой (одни и те же входные данные всегда приводят к одним и тем же выходным данным). Бывают случаи, когда это может быть полезно или даже желательно (например, вы хотите, чтобы научное моделирование повторялось, или вы пытаетесь выяснить, почему ваш генератор случайных подземелий дает сбой).

Но часто это не то, что нужно. Если вы пишете игру «hi-lo» (высоко-низко) (где у пользователя есть 10 попыток угадать число, а компьютер сообщает ему, является ли его предположение слишком высоким или слишком низким), вы не хотите, чтобы программа каждый раз выбирала одни и те же числа. Итак, давайте подробнее посмотрим, почему это происходит, и как мы можем это исправить.

Помните, что каждое число в последовательности ГПСЧ определенным образом генерируется из предыдущего числа. Таким образом, при любом одном и том же начальном числе ГПСЧ всегда будут генерировать одну и ту же последовательность чисел! Мы получаем ту же последовательность, потому что наше начальное число всегда 5323.

Чтобы сделать всю нашу последовательность случайной, нам нужен способ выбрать начальное число, которое не является фиксированным значением. Первый ответ, который, вероятно, приходит в голову, – нам нужно случайное число! Это хорошая мысль, но если нам нужно случайное число для генерации случайных чисел, тогда мы попадаем в уловку-22. Оказывается, нам на самом деле не нужно, чтобы наше начальное число было случайным – нам просто нужно выбирать что-то, что меняется при каждом запуске программы. Затем мы можем использовать наш ГПСЧ для генерации уникальной последовательности псевдослучайных чисел из этого начального числа.

Общепринятым методом для этого является использование системных часов. Каждый раз, когда пользователь запускает программу, время будет другим. Если мы используем это значение времени в качестве начального числа, тогда наша программа при каждом запуске будет генерировать другую последовательность чисел!

Вот та же программа, что и выше, но с вызовом time() в качестве начального числа:

Теперь наша программа будет каждый раз генерировать новую последовательность случайных чисел! Запустите ее пару раз и убедитесь сами.

Генерация случайных чисел между двумя произвольными значениями

Вот короткая функция, которая преобразует результат rand() в нужный диапазон:

Дополнительный материал: как работает предыдущая функция?

Функция getRandomNumber() может показаться немного сложной, но всё не так уж плохо.

Мы делаем это в пять этапов:

Дополнительный материал: почему в предыдущей функции мы не используем оператор остатка от деления ( % )?

Один из наиболее частых вопросов, которые задают читатели, – почему мы используем деление в приведенной выше функции вместо взятия остатка от деления ( % ). Короткий ответ заключается в том, что метод с остатком от деления имеет тенденцию смещаться в пользу малых чисел.

Давайте посмотрим, что бы произошло, если бы вместо этого приведенная выше функция выглядела так:

Теперь давайте посчитаем все возможные исходы:

Посмотрите на распределение результатов. Результаты с 0 по 2 появляются дважды, а с 3 по 6 – только один раз. Этот метод имеет явный уклон в сторону низких результатов. Экстраполируя это: большинство случаев, связанных с этим алгоритмом, будут вести себя аналогичным образом.

Расчет всех возможных исходов:

Здесь всё еще есть небольшое смещение в сторону меньших чисел (0, 2 и 4 появляются дважды, тогда как 1, 3, 5 и 6 появляются один раз), но результаты распределены гораздо более равномерно.

Несмотря на то, что getRandomNumber() немного сложнее для понимания, чем альтернатива с остатком от деления, мы выступаем за метод с делением, потому что он дает менее предсказуемый результат.

Что такое хороший генератор псевдослучайных чисел?

Как я уже упоминал выше, ГПСЧ, который мы написали, не очень хороший. В этом разделе мы обсудим причины, почему. Это дополнительный материал, потому что он не имеет прямого отношения к C или C++, но если вам нравится программировать, вам, вероятно, всё равно будет интересно.

Чтобы быть хорошим, ГПСЧ должен обладать рядом свойств:

Во-первых, ГПСЧ должен генерировать каждое число примерно с одинаковой вероятностью. Это называется равномерностью распределения. Если одни числа генерируются чаще других, результат программы, использующей ГПСЧ, будет искажен!

Например, предположим, вы пытаетесь написать генератор случайных предметов для игры. Вы выбираете случайное число от 1 до 10, и если результат равен 10, с монстра выпадет мощный предмет вместо обычного. Вы ожидаете, что это произойдет с вероятностью 1 из 10. Но если результаты простого ГПСЧ распределены неравномерно, и он генерирует намного больше десяток, чем должен, ваши игроки в конечном итоге получат больше редких предметов, чем вы предполагали, что, возможно, упростит вашу игру.

Создание ГПСЧ, дающих равномерно распределенные результаты, является сложной задачей, и это одна из основных причин, по которой ГПСЧ, который мы написали в начале этого урока, не очень хороший.

В-третьих, ГПСЧ должен иметь хорошее пространственное распределение чисел. Это означает, что он должен возвращать низкие, средние и высокие значения, казалось бы, случайным образом. ГПСЧ, который вернул все низкие значения, а затем все высокие значения, может быть равномерно распределенным и непредсказуемыми, но он всё равно приведет к смещенным результатам, особенно если количество случайных чисел, которые вы реально используете, невелико.

В-четвертых, все ГПСЧ являются периодическими, что означает, что в какой-то момент сгенерированная последовательность чисел начнет повторяться. Длина последовательности до того, как ГПСЧ начинает повторяться, называется периодом.

Например, вот первые 100 чисел, сгенерированных из ГПСЧ с плохой периодичностью:

Вы можете заметить, что он сгенерировал 9 как второе число и снова 9 как 16-е число. ГПСЧ застревает, постоянно генерируя последовательность между этими двумя девятками: 9-130-97-64-31-152-119-86-53-20-141-108-75-42- (повтор).

Это происходит потому, что ГПСЧ детерминированы – при некотором наборе входных значений они каждый раз будут выдавать одно и то же выходное значение. Это означает, что как только ГПСЧ встречает набор входных данных, которые он использовал ранее, он начинает производить ту же последовательность выходных данных, которую он создавал раньше, что приводит к циклу.

Хороший ГПСЧ должен иметь длительный период для всех начальных значений. Разработка алгоритма, отвечающего этому свойству, может быть чрезвычайно сложной задачей – большинство ГПСЧ будут иметь длительные периоды для одних начальных значений и короткие периоды для других. Если пользователь выберет начальное число с коротким периодом, тогда ГПСЧ не будет работать хорошо.

Несмотря на сложность разработки алгоритмов, отвечающих всем этим критериям, в этой области было проведено множество исследований из-за ее важности для научных вычислений.

std::rand() – посредственный ГПСЧ

Одним из основных недостатков rand() является то, что RAND_MAX обычно устанавливается равным 32767 (по сути, 15 бит). Это означает, что если вы хотите генерировать числа в большем диапазоне (например, 32-битные целые числа), rand() не подходит. Кроме того, rand() не подходит, если вы хотите генерировать случайные числа с плавающей запятой (например, от 0,0 до 1,0), что часто бывает полезно при статистическом моделировании. Наконец, rand() имеет относительно короткий период по сравнению с другими алгоритмами.

Тем не менее, rand() идеально подходит для обучения программированию и для программ, в которых высококачественный ГПСЧ не является необходимостью.

Для приложений, где полезен высококачественный ГПСЧ, я бы порекомендовал вихрь Мерсенна (Mersenne Twister) (или один из его вариантов), который дает отличные результаты и относительно прост в использовании. Вихрь Мерсенна был введен в C++11, и мы покажем, как его использовать позже в этом уроке.

Отладка программ, использующих случайные числа

Программы, использующие случайные числа, может быть трудно отлаживать, потому что программа при каждом запуске может вести себя по-разному. Иногда это может сработать, а иногда нет. При отладке полезно следить за тем, чтобы ваша программа каждый раз выполняла один и тот же (неправильный) путь. Таким образом, вы можете запускать программу столько раз, сколько необходимо, чтобы определить причину ошибки.

По этой причине при отладке полезно установить случайное начальное число (через std::srand ) на определенное значение (например, 0), которое вызывает ошибочное поведение. Это гарантирует, что ваша программа каждый раз будет генерировать одни и те же результаты, что упростит отладку. Как только вы обнаружите ошибку, вы можете снова использовать системные часы, чтобы снова начать генерировать рандомизированные результаты.

Получение лучших случайных чисел с помощью вихря Мерсенна

Вот небольшой пример, показывающий, как сгенерировать случайные числа в C++11 с помощью вихря Мерсенна:

Примечание автора

До C++17 вам нужно было после типа добавить пустые скобки для создания die
std::uniform_int_distribution<> die

Вы можете заметить, что вихрь Мерсенна генерирует случайные 32-битные целочисленные значения без знака (а не 15-битные целочисленные значения, как std::rand() ), что дает гораздо больший диапазон. Также существует версия ( std::mt19937_64 ) для генерации 64-битных целочисленных значений без знака.

Случайные числа в нескольких функциях

В приведенном выше примере генератор псевдослучайных чисел создается для использования в одной функции. Что произойдет, если мы захотим использовать генератор случайных чисел в нескольких функциях?

Хотя вы можете создать статическую локальную переменную std::mt19937 в каждой функции, которая в ней нуждается (статическая, чтобы она была инициализирована только один раз); но это немного излишне – чтобы каждая функция получала начальное значение для генератора случайных чисел и поддерживала свой собственный локальный генератор. В большинстве случаев лучшим вариантом является создание глобального генератора случайных чисел (внутри пространства имен!). Помните, как мы говорили вам избегать неконстантных глобальных переменных? Это исключение (также обратите внимание: std::rand() и std::srand() обращаются к глобальному объекту, поэтому для этого есть прецедент).

Использование библиотеки генерирования случайных чисел

Вот приведенная выше программа, модифицированная под использование библиотеки Effolkronium:

Помогите! Мой генератор случайных чисел генерирует одну и ту же последовательность случайных чисел!

Если ваш генератор случайных чисел при каждом запуске вашей программы генерирует одну и ту же последовательность случайных чисел, вы, вероятно, неправильно его инициализировали. Убедитесь, что вы инициализируете его значением, которое изменяется при каждом запуске программы (например, std::time(nullptr) ).

Помогите! Мой генератор случайных чисел всегда генерирует одно и то же первое число!

Реализация rand() в Visual Studio и некоторых других компиляторах имеет недостаток – первое сгенерированное случайное число не сильно меняется для похожих начальных значений. Это означает, что при использовании std::time(nullptr) для инициализации вашего генератора случайных чисел первый результат rand() не сильно изменится при последующих запусках. Однако на результаты последующих вызовов rand() это не повлияет, и они будут достаточно рандомизированы.

Решение здесь, и хорошее практическое правило в целом, – отбросить первое число, сгенерированное генератором случайных чисел.

Помогите! Мой генератор случайных чисел вообще не генерирует случайные числа!

Если ваш генератор случайных чисел генерирует одно и то же число каждый раз, когда вы запрашиваете случайное число, то вы, вероятно, либо повторно инициализируете генератор случайных чисел перед генерацией случайного числа, либо создаете новый генератор случайных чисел для каждого получения случайного числа.

Вот две функции, которые показывают проблему:

В обоих случаях генератор случайных чисел инициализируется перед каждой генерацией случайного числа. Это приведет к тому, что каждый раз будет генерироваться одно и то же число.

В верхнем случае std::srand() повторно инициализирует встроенный генератор случайных чисел перед вызовом rand() (с помощью getRandomNumber() ).

В нижнем случае мы создаем новый вихрь Мерсенна, инициализируем его, генерируем одно случайное число и затем уничтожаем его.

Для получения случайных результатов вы должны инициализировать генератор случайных чисел только один раз (обычно при инициализации программы для std::srand() или в точке создания для других генераторов случайных чисел), а затем использовать тот же генератор случайных чисел для каждого последующего генерируемого случайного числа.

Предупреждение

Пример getOtherRandomNumber() – одна из самых распространенных ошибок, которые допускаются в тестах. Вы не заметите, что getOtherRandomNumber() не работает, пока вы не начнете вызывать его чаще, чем один раз в секунду (поскольку начальное число изменяется только один раз в секунду). Не забудьте сделать генератор случайных чисел статическим или объявить его вне функции.

Создавая непредсказуемость. Примеры использования генераторов случайных чисел

Привет, Хаброжители! У нас вовсю продолжается распродажа «Старый Новый год».

Кто пытается арифметическими методами генерировать случайные числа, тот, конечно, живет во грехе. Поскольку, как указывалось уже неоднократно, нет такого феномена, как случайное число — есть только методы для получения случайных чисел.

Генераторы случайных чисел (ГСЧ) – важнейшая составляющая разнообразных процессов, связанных с компьютерными программами, таких как криптография, моделирование, машинное обучение, игры, программирование, азартные игры, научные исследования – список можно продолжать. Но может возникнуть вопрос: как именно получить по-настоящему случайное значение, и почему это важно?

Оказывается, спонтанность — не самая сильная сторона компьютеров. Они
могут выполнять только те действия, на которые запрограммированы. Благодаря
ГСЧ, компьютеры приобретают способность генерировать уникальные неравномерно
распределенные числа. Иными словами, ГСЧ помогает компьютеру моделировать
непредсказуемость.

Два типа генераторов случайных чисел

Генераторы случайных чисел бывают двух разных типов: генераторы истинно случайных чисел (ГИСЧ) и генераторы псевдослучайных чисел (ГПСЧ) [1]. ГИСЧ считаются «истинными», так как используют в качестве источника энтропии внешний источник, расположенный за пределами компьютерной программы – например, погоду, атмосферные помехи или промежутки времени, в течение которых вы удерживаете клавиши на клавиатуре вашего компьютера.

Более строгие научные методы связаны с измерением радиоактивного распада атома [2]. Согласно квантовой теории, невозможно узнать наверняка, когда произойдет акт деления ядра, так что это, в сущности, «чистая случайность». Генерация истинно случайных чисел – это по-настоящему захватывающая тема, и мы посвятили ей целую статью, которая находится здесь.

ГИСЧ отлично подходят для создания подлинно случайных чисел, но работа таких генераторов зачастую отличается высокой вычислительной сложностью и не масштабируется, поскольку они зависят от внешних источников данных и от сенсоров.

Генерация псевдослучайных чисел (синий) и генерация истинно случайных чисел (белый)

Генераторы псевдослучайных чисел

Кажется, что ГПСЧ генерируют случайные числа, но на самом деле это только кажется [3]. Они сравнительно широко используются благодаря своей скорости и воспроизводимости результатов, поэтому они очень хорошо подходят для применения при моделировании и в играх. В сущности, ГПСЧ – это алгоритмы, использующие математические формулы или просто предвычисленные таблицы для выдачи последовательностей чисел [4]. Возьмем, к примеру, линейный конгруэнтный генератор (ЛКГ). В его составе используется начальное значение, множитель, инкремент и модуль.

В ЛКГ для запуска алгоритма используется одиночное начальное значение. ЛКГ решает такое уравнение: (seed * multiplier + increment) mod m = output

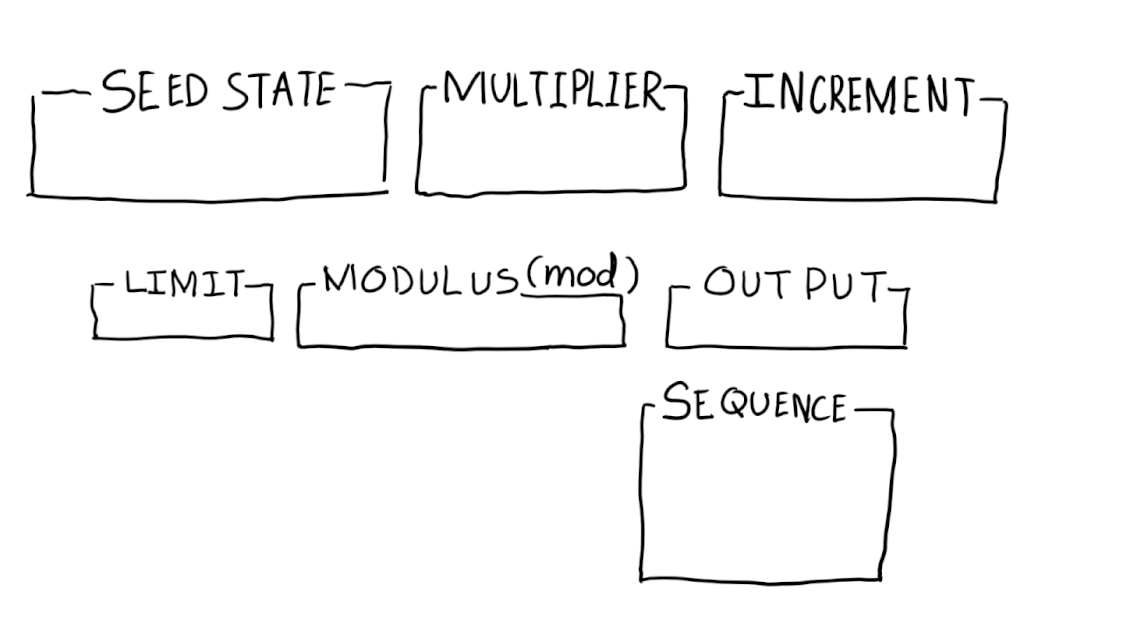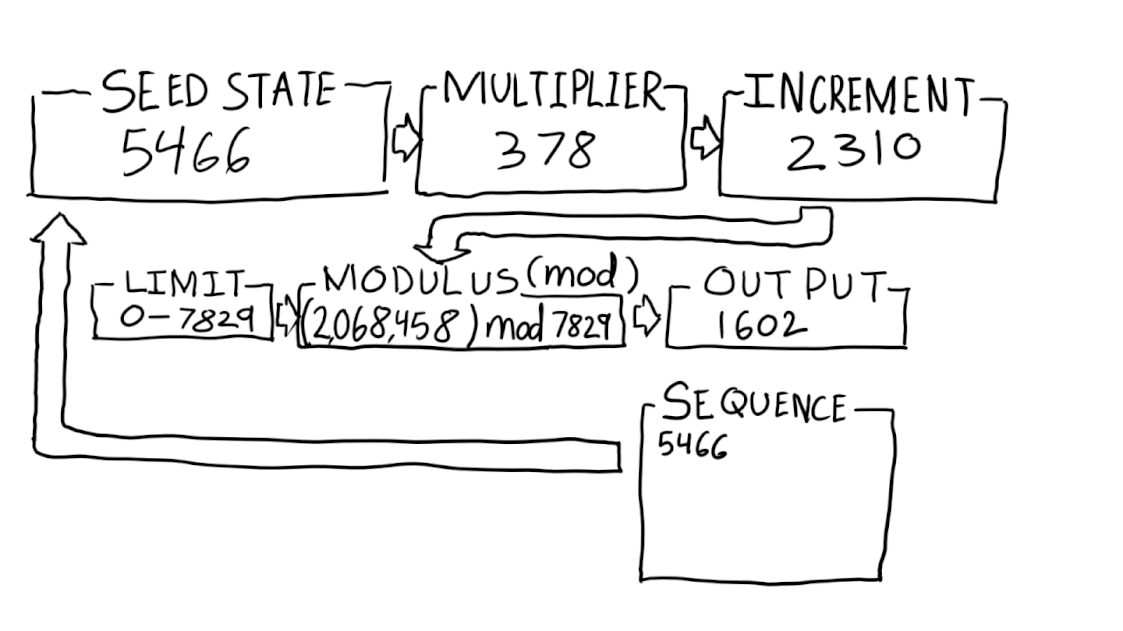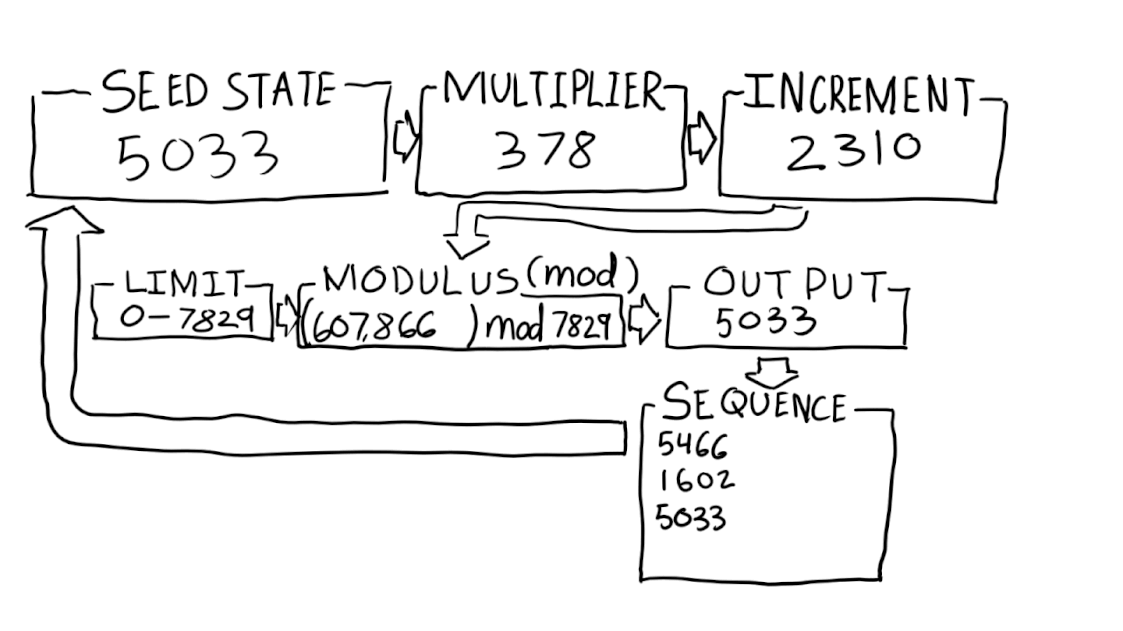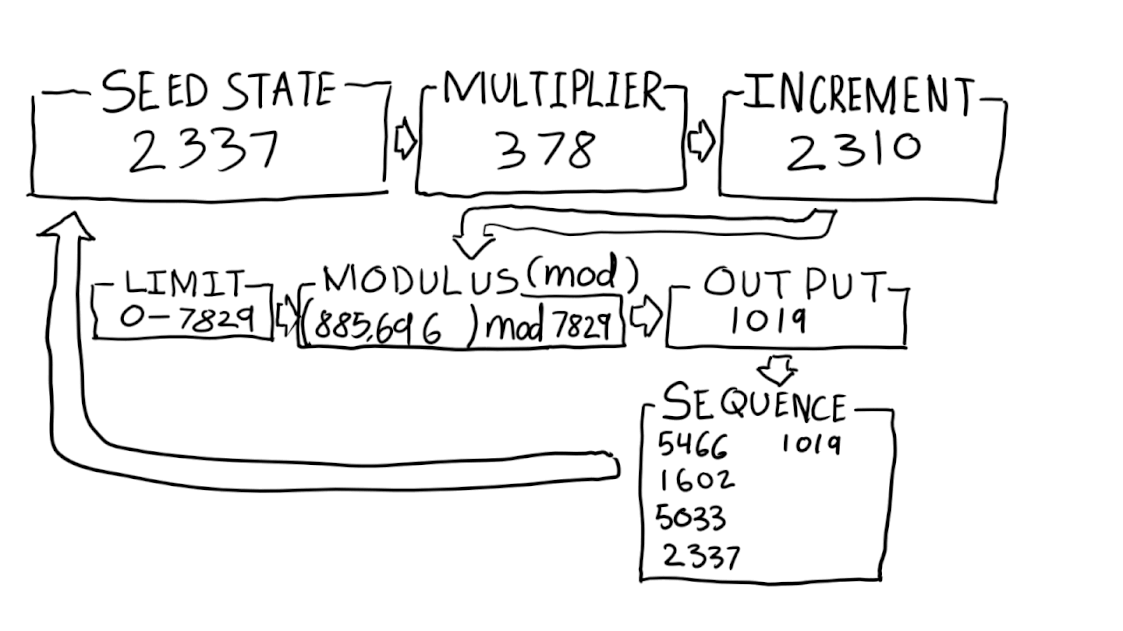
Рано или поздно, после некоторого количества попыток, последовательности начнут повторяться. Эта величина называется «период» и является мерой количества уникальных чисел в последовательности. ЛКГ не используются при шифровании, поскольку не обеспечивают достаточно надежной случайности. У них короткие периоды, а их паттерны равномерны.

В основе большинства ГПСЧ для шифрования лежит Вихрь Мерсенна. Этот генератор псевдослучайных чисел был разработан в 1997 году Макото Мацумото и Такудзи Нисимура и в настоящее время является наиболее распространенным неспециализированным ГПСЧ [5]. Назван он так потому, что имеет период 2¹⁹⁹³⁷− 1, такова длина простого числа Мерсенна. Вихрь Мерсенна по умолчанию используется во многих программных системах, в частности, в Microsoft Excel, MATLAB, Free Pascal, PHP, Python, R, Ruby и C++. Также он обычен в играх. К нему прибегают во многих системах, так как он позволяет быстро генерировать высококачественные псевдослучайные числа.

Способы использования игр

По мере того, как компьютерные игры становятся все реалистичнее, растет потребность и в более качественных генераторах случайных чисел. Сейчас ГПСЧ используются для создания геймплея, графики и обеспечения многих аспектов разработки игр. Когда ваш персонаж бьет противника, в игре требуется случайное число, чтобы аппроксимировать разброс нанесенного ущерба. В игре с ультрареалистичной графикой ГСЧ делегируется имитация отражений света, чтобы не перенапрягать процессор. В Minecraft случайное начальное значение используется для процедурной генерации мира вокруг вашего персонажа.

Игры такого типа, основанные на так называемой «процедурной генерации», в последние годы приобрели большую популярность. Причина проста: в них не приходится все делать вручную. Процедурный генератор – это система, использующая ГСЧ для создания целого мира по чисто случайному принципу [6]. В случае с “No Man’s Sky” в игре генерируется целая Вселенная. Процедурная генерация позволяет очень сильно экономить память, в то же время создавая почти неограниченное количество игровых локаций и персонажей. Без ГСЧ сделать это было бы просто невозможно, поскольку слишком сильно затрачивались бы ресурсы, и на большинстве устройств игра бы подвисала.

Конечно, здесь есть и недостатки. Для генерации каждой планеты в “No Man’s Sky” используется 64-разрядное начальное значение. Это число скармливается генератору биомов для создания ландшафта и других разнообразных атрибутов планеты. Но 64-разрядного числа в данном случае недостаточно, поэтому планеты не отличаются существенным разнообразием.

Порождающая последовательность запускается в игре всякий раз, когда вы входите в новую звездную систему [7]. Сначала вы видите большие разнообразные планеты с голубыми океанами и пышными зелеными лесами. Как только вы приступаете к исследованию планет, начинают вырисовываться различные варианты окружающей среды. Избыточные ландшафты и животные равномерно распределяются по поверхности планеты, и закономерности становятся очевидными.

С технической точки зрения, эти планеты получаются методом генерации случайных чисел, но ни одна из них не оставляет по-настоящему уникального впечатления. Игра может справляться только с небольшой вариативностью окружающей среды, отчасти из-за ограничений того ГПСЧ, который в ней используется. Чтобы справиться с такой дилеммой, нужен генератор случайных чисел с более длинным случайным значением. Если увеличить длину начального значения, получим больше переменных, но одного лишь этого будет мало. Один из атрибутов случайности заключается и в дисперсии чисел. Вы не хотите, чтобы одно и то же число попалось вам двенадцать раз подряд. Случайность получается и из того, насколько неравномерно распределены последовательности чисел. Вот почему фактор случайности так важен в играх.

Равномерность распределения псевдослучайных чисел можно проверить при помощи симуляции по методу Монте-Карло [8]. Методы Монте-Карло – это тип алгоритмов, которые раз за разом делают случайную выборку для получения численного результата. Их основная идея – в решении задач методом подбора случайных значений.

Оценка значения числа Пи методом Монте-Карло

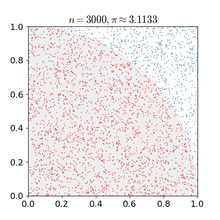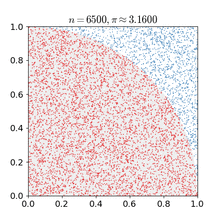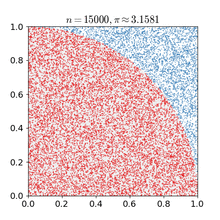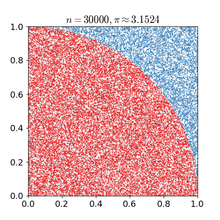
Обычно они используются для оценки неизвестных соотношений и областей. На рисунке выше метод Монте-Карло применяется для оценки значения числа Пи. Чтобы методы Монте-Карло были эффективны, в них не обязательно требуются истинно случайные числа. Часто при помощи детерминированных псевдослучайных последовательностей оказывается просто тестировать и повторно прогонять симуляции [9]. Рассмотрим, например, как робот-пылесос Roomba ориентируется по плану комнат в доме.

Роботы-уборщики наподобие Roomba используют для навигации безмодельный фреймворк машинного обучения [10]. Таким образом, они учатся методом проб и ошибок: вы формулируете роботу, какую цель нужно достичь, но не предоставляете ему конкретного плана действий.

Пылесос Roomba 980 строит карту «окрестностей», прибираясь в доме

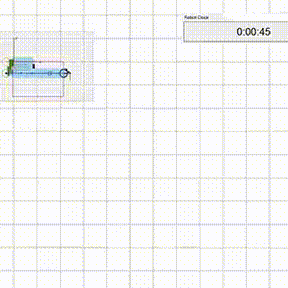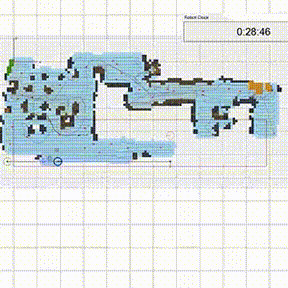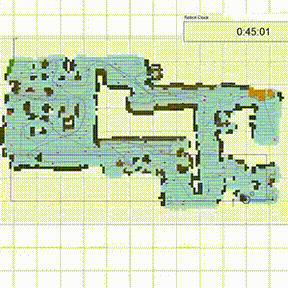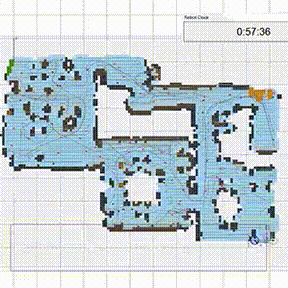
Tакой безмодельный фреймворк использует симуляцию по методу Монте-Карло, чтобы смоделировать планировку дома. Вместо того, чтобы просто покрывать всю возможную площадь дюйм за дюймом, он случайным образом выбирает точки, которые нужно найти, и так уточняет планировку. Входящие данные от сенсоров он использует, чтобы проверить, обошел ли уже весь пол. Закончив поиски, он возвращается в точку, которая соответствует началу координат.

Рандомизация домена (DR) – еще один способ использования случайности в машинном обучении. DR – это фреймворк машинного обучения, основанный на моделях. В нем применяется фиксированный набор правил, по которым учится ИИ [11]. Он используется в открытом проекте из области ИИ, связанном с моделированием ловкости рук.

Варианты манипуляций, автономно изученные роботом Dactyl

Dactyl – это робот, обученный на множестве случайно подобранных симуляций, при помощи которых компьютер освоил естественные движения рук. Проект показал, что опыт обучения, заложенный в модель, составляет 100 лет. Машинное обучение такого рода было бы недостижимо, если бы учебные множества данных для него не генерировались при помощи ГСЧ.

Варианты использования в криптографии

Вы когда-нибудь задумывались, каковы механизмы шифрования в ваших полях с паролями и в браузере? Вы догадались: в основе цифрового шифрования лежат случайные числа [12]. Всякий раз, когда ваш браузер пытается обратиться за онлайновой информацией, она шифруется по методу SSL, что означает «слой защищенных сокетов».

Процесс начинается так:

Сначала ваш браузер запрашивает идентификатор сервера.

Затем веб-сервер направляет вашему браузеру в ответ на этот запрос SSL-сертификат.

Браузер/сервер проверяют, можно ли доверять SSL-сертификату. Если можно, то на веб-сервер отправляется соответствующее сообщение.

Веб-сервер отправляет обратно подтверждение, снабженное цифровой подписью и позволяющее начать сеанс, зашифрованный по технологии SSL.

Зашифрованные данные совместно используются браузером/сервером с одной стороны и веб-сервером с другой стороны.

В принципе, именно так и происходит шифрование всех ваших данных, передаваемых онлайн.

История тайн

Использование фактора случайности для шифрования сообщений восходит ко временам древнего Рима. Римляне использовали шифр Цезаря, чтобы зашифровывать военные сообщения случайным ключом. В перемешивании для такого шифра использовалось всего 26 букв, поэтому вероятность взломать его составляла 1/26. Враг мог путем перебора попробовать все буквы латинского алфавита, и в таком случае на взлом кода ушло бы несколько часов, но к тому времени зашифрованные приказы уже были бы неактуальны.

Шифр Цезаря

По стандартам современной криптографии используется так называемая система одноразовых блокнотов. При использовании этого метода каждый символ в сообщении заменяется случайной буквой. Такой подход значительно снижает вероятность, что сообщение будет расшифровано. Допустим, вы хотите зашифровать имя “Alice”:

При рандомизации каждого символа в сообщении сложность его расшифровки возрастает экспоненциально. В случае с “Alice”, как в вышеприведенном примере, вероятность расшифровать это слово с первой попытки составляет около одного к 12 миллионам (26*26*26*26*26). Чем длиннее ключ, тем сильнее шифр.

Если вас интересует по-настоящему сложное шифрование, обратите внимание на SHA-256 [13]. SHA означает “Secure Hash Algorithm” (алгоритм криптографического хеширования). Он обычен в блокчейнах. Хеш-функция – это тип математической функции, преобразующей данные в отпечаток, именуемый «хеш-значением». Хеш-алгоритм – это функция, принимающая входные данные и преобразующая их в вывод фиксированной длины. Хеш-функция однонаправленная. Невозможно обратить данные из ее хеша; можно пройти путь от входных данных до хеша, но не наоборот.

У SHA-256 2^256 возможных исходов. Это число невероятно велико. Если бы все компьютеры на планете были задействованы для расшифровки всех возможных сигнатур этого сообщения, то на эту работу потребовался бы срок, в 37 раз превышающий возраст Вселенной. SHA-256 – основа защиты большинства блокчейнов, а также стандартный метод шифрования в АНБ и ЦРУ. Это одна из причин, по которым с технологиями блокчейна связаны такие большие ожидания.

Заключение

Истинная случайность непредсказуема, и ее сложно сгенерировать в компьютерных системах. В мире математики, где повсюду используются записанные данные и формулы для прогнозов, все сложнее найти что-то случайное. Но в этом и ценность. Люди, привыкшие искать паттерны, всегда будут ценить то, что не поддается предсказанию, особенно при защите приватности, которой сегодня уделяется такое внимание. Говорим ли мы о расчете при моделировании, о шифровании сообщений или о повышении фактора случайности в работе игровых автоматов, генераторы случайных чисел оказываются незаменимы в нашем обществе.

Создаём аппаратный генератор случайных чисел

Я хочу представить вашему вниманию программно-аппаратный вариант получения случайных чисел. Забегая вперёд, скажу, что данный вариант не единственный, и этот пост открывает мою небольшую серию статей о получении, генерации и изучении случайных чисел, или точнее сказать просто случайностей.

Магия случайных чисел меня привлекала с раннего детства. Дата рождения, смерти, одарённость, выигрыш в лотерею, билет на экзамене и т. д. — всё это случайные события. С другой стороны, глядя на наш мир, понимаешь, что случайностей не бывает. Или как говорят учёные: Случайность – это не исследованная закономерность. Мне всегда было интересно, почему вот наступает именно это случайное событие, а не другое? Почему монетка, брошенная сейчас, выпала решкой, и может ли что-то повлиять на это событие? Какие взаимовлияния случайностей друг на друга, можем ли мы влиять на эти случайные величины? Все эти вопросы находятся пока за гранью науки, но интересно на них найти ответ. К сожалению, в институте, я не достаточно хорошо оценил предмет «Теорию вероятности» и просто прошёл его, за что и получил минус жизненной кармы. По сему сегодня я всячески стараюсь наверстать упущенное.

Постановка задачи

Для различных инженерных и вычислительных задач требуется поиск случайных чисел. Причём, чем выше энтропия числа, чем ниже его закономерность и предсказуемость, тем лучше. Все мы пользовались в программировании функцией генератора случайных чисел. На самом деле, все эти числа псевдослучайны. Они могут вычисляться по очень сложному алгоритму, или вообще представлять собой «слепок» случайных шумов системы (как например /dev/random и /dev/urandom ). Но всё же, как ни странно, эти случайные числа предсказуемы. Самый очевидный способ получения случайных чисел, это брать их извне. Ведь наш реальный мир — это громадный генератор случайных величин. Конечно же все эти величины тоже псевдослучайны, но их закономерности и взаимозависимости проследить невозможно, из-за бесконечного количества вариантов происходящих событий. Надо так же понимать, что нельзя рассматривать случайные числа, как числа появляющиеся в замкнутой системе, поскольку на них идёт влияние бесконечного множества внешних факторов. Тогда, если разобраться, каждое событие совершенно не случайно и имеет свою закономерность. Просто учесть все взаимовлияния (а их бесконечно много), невозможно, по сему для простоты принимают многие события случайными.

Наиболее простой способ получения случайных чисел – это снятие шумов со звуковой карты компьютера. При чём, чем хуже звуковая карта, тем лучше она шумит. В качестве дополнительного источника шума, опционально, можно подключить любой радиоприёмник, настроенный на шум, к линейному входу звуковой карты.

+ + Sound card = Random generator

К слову сказать тепловой шум в полупроводниках, обусловленный тепловым движением атомов, является самым распространенным источником случайных чисел, например при генерации ключей в SMART-картах.

Правда хочу отметить, что известны случаи взломов устройств со встроенным шифрованием (SMART-карты), которые для генерации случайных чисел используют принцип тепловых шумов в полупроводниках. Взлом осуществляется достаточно просто – заморозкой в жидком азоте самого чипа, в результате чего тепловые шумы падают почти до нуля.

Гистограмма частоты числа наблюдений случайной величины

Случайные величины колеблются возле какого-то одного значения (математического ожидания этой величины). Положим, мы снимем несколько тысяч случайных точек, найдём максимальное и минимальное значение, которое принимает случайная величина. Возьмем интервал от минимального значения, которое принимает случайная величина, до максимального значения, которое может принимать случайная величина. Разобьём этот интервал на равные интервалы, например на пятьдесят. Ололо пыщ-пыщ, никто же не читает. И посчитаем, сколько случайных величин попадёт в каждый интервал, то мы получим диаграмму распределения случайной величины. Надо сказать, величина рассеяния случайного события определяется, и измеряется она дисперсией. Данный способ построения диаграммы рассеяния случайной величины называется интервальным. Он основан на разбиении исходных численных значений на интервалы.
Если на пальцах представить, что такое распределение, то это будто мы сыпем из ладони песок, в соответствии с изменением сигнала по вертикальной оси.
Проиллюстрирую примером. Колебания маятника. Если его развернуть во времени, то получится синусоида f(x)=sin(x) – это исходный график, распределение которого мы ищем. Если к этому маятнику приделать солонку, которая сыпет песок, то она и будет рисовать диаграмму распределения. Продемонстрируем как это выглядит

Пример куска кода для построения:

График «распределения» синуса.

Если говорить о солонке на маятнике, то становится понятно, почему получился такой график. В высшей точке колебания маятника, которая соответствует пикам синусоиды, движение замедляется и там песочек должен образовывать «горки», а в точке нуля должно быть минимальное количество песка, т.к. это место маятник проходит с максимальной скоростью.

Распределение Гаусса или нормальное

Наилучшим образом это демонстрируется на этом видео, с использованием доски Гальтона ru.wikipedia.org/wiki/Доска_Гальтона, взятым из курса лекций МИФИ

В моём институте тоже был аналогичный опыт, и преподаватель произнёс сакральную фразу, которая произвела на меня большое впечатление: Я пятьдесят лет провожу этот опыт, и всегда получаю одну и ту же картину. Формально, ничего не мешает частицам лечь равномерно, однако всегда мы получаем распределение Гаусса.

Распределению Гаусса подчиняются различные величины. Например, стрельба по мишени – пули будут ложится в мишень по распределению Гаусса. Наиболее кучно в десятки и наименее по краям. Разумеется, электрический шум (если он не вызван наводкой электрической сети), тоже будет подчиняться этому распределению.

Распределение Пуассона

Существуют и другие виды распределения случайной величины. Например, существует распределение Пуассона. Одна из особенностей распределения Пуассона является то, что случайная величина является дискретной. Самой лучшей иллюстрацией событий распределения Пуассона могут быть звонки в какой-нибудь call-центр. Количество звонков поступивших за единицу времени будет случайной величиной. Или вот, пока я отлаживал программу, о которой скажу ниже, я измерял интервалы нажатия на клавишу. Интервалы измерял микроконтроллер, считая прошедшее количество тактов между каждым нажатиями. Я сделал несколько тысяч нажатий и получил вот такую диаграмму.

Диаграмма распределения частоты нажатий на кнопку.

Кстати говоря, я не зря сказал, что случайных величин не бывает. Здесь я нажимаю пальцем на кнопку. Случайность интервалов нажатия обусловлена тем, что мой мозг занимается обработкой различных сигналов, мечтами о «вечном», мысли о программе и т.д. Плюс так же, сигналы от мозга достигают конечностей тоже не со скоростью света, т.к. ионный обмен при передаче сигналов обусловлен химическими процессами в моём организме и т.д. и т.п. В результате мы имеем совершенно случайную интенсивность нажатий.

Надо сказать, что распределению Пуассона подчиняются так же и регистрация радиоактивных частиц с помощью дозиметров.

Равномерное распределение

Самое ценное распределение, с точки зрения программиста – это равномерное распределение. Когда случайные числа любой длинны, встречаются одинаково часто на всём заданном диапазоне. Пример из жизни такого распределения, это время ожидания транспорта на остановке, при учёте того, что транспорт ходит с одинаковыми интервалами времени. Вы можете придти и тут же сесть в маршрутку, тогда время вашего ожидания будет равно нулю, или прямо из под носа уйдёт эта маршрутка. Тогда время вашего ожидания будет равно интервалу следования маршруток. Но, как правило, приходится ждать. И если мы разобьём время ожидания на интервалы dt и построим гистограмму частот попадания на маршрутку, допустим на несколько лет, то она будет линией.

Гистограмма частот попадания на свою маршрутку.

По вертикали отложено количество попаданий на маршрутку, а по горизонтали время ожидания маршрутки.

Например, гистограмма распределения данных, получаемых /dev/random

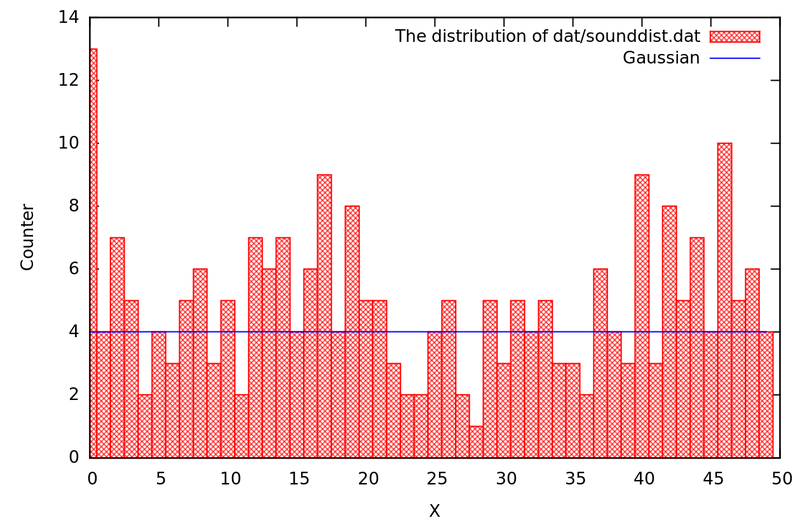
Гистограмма системного генератора случайных чисел

Вы можете сами получить данную гистограмму, заменив в моей программе, о которой будем говорить ниже, /dev/audio (/dev/dsp) на /dev/random (инициализация звуковой карты никак не влияет на генератор случайных чисел).
Надо заметить, что я раз 15 перезапускал программу, чтобы получить гистограмму наиболее близкую к теоретической. Это говорит о несовершенстве этого генератора случайных чисел. Синяя линия показывает, как эта гистограмма должна выглядеть в идеале.

Другие типы распределений можно посмотреть на этом рисунке

Основные типы распределения случайных величин.

Меньше слов и больше дела

Наверное, я уже успел надоесть своим любительским тервером. По сему, от теории переходим к практике. Моя программа написана под Linux, и тестировалась на Ubuntu 10.10. Для построения диаграмм в системе должен быть установлен пакет gnuplot, без него программа работать не будет.
К слову сказать, я всячески рекомендую всем инженерам разобраться с кроссплатформенным программным пакетом gnuplot. Это идеальный пакет для построения любых графиков. После работы с ним, я забыл, что такое построение графиков в MS Excel как страшный сон. День-два разобраться, и потом на лабораторках в институте или на работе вы будете радовать себя и других оригинальными графиками высокого качества. Несомненный плюс, что данный пакет можно использовать в в программах, для быстрого и простого построения графиков.
На этом о гнуплоте всё, я не буду подробно останавливаться, как же я строил графики. Лучше как-нибудь отдельно напишу пост, посвящённый этому замечательному пакету.

Итак, что же делает моя программа. Она в течении трёх секунд

С частотой дискретизации 96000 Гц

Записывает данные типа signed short

С одного входного канала звуковой карты

Данные записываются сохраняются в массив

После чего инициализируется звуковая карта, и в течении трёх секунд считываются данные. Я честно признаюсь, что полностью всех особенностей работы со звуковой картой я не исследовал. Не пробовал читать в стереорежиме, принимать 24-х разрядные данные. Я пробовал менять только частоту дискретизации. Так же хочу сказать, что получение данных со звуковой карты выходит не всегда стабильным. После перезагрузки системы я перезапускаю эту программу несколько раз, чтобы получить гистограмму. Иногда она выдаёт совершенно непонятные значения. С чем это связанно, я так же не знаю.
После инициализации звука и чтения всех данных в массив buf, мы находим минимальное и максимальное значение массива. После чего сохраняется не отсортированный массив в array.dat (из которого можно потом построить осциллограмму снимаемых данных). Далее массив сортируется функцией

Для отладки сохраняется отсортированный массив в файл error.log.

Дальше мы находим дельту – интервал ячейки, в который мы будем складывать наши значения:

Выделяем память для массива распределения. Выделение память сделано для универсальности, чтобы можно было динамически менять размер распределения.

После чего начинаем считать, какие же значения попали в какой интервал, или проще говоря строить распределение случайных величин:

Уже по этому графику можно построить диаграмму распределения случайной величины. Но я хочу сравнить практическое распределение с теоретическим графиком Нормального распределения, который строится по формуле взятой из википедии ru.wikipedia.org/wiki/Нормальное_распределение:

Для построения по этой формуле нам необходимо найти два параметра: Математическое ожидание и дисперсию. Как я говорил, математическое ожидание – это величина, вокруг которой колеблется случайные числа. Дисперсия – это мера рассеяния. Есть два пути нахождения этих величин – из исходного массива и из получившейся диаграммы. Математическое ожидание я нахожу двумя способами, но использую последний, дисперсию нахожу только последним способом.
Математическое ожидание в нашем случае – это просто среднее значение всех случайных величин. Находим его так

Дисперсия определяется как квадратичное отклонение случайной величины от математического ожидания. Мы его находим следующим образом:

Это и есть рассчёт распределения Гаусса, с использованием математического ожидания и дисперсии.

Полученную программу можно скачать тут: narod.ru/disk/32347266001/sound_distribution.tar.gz.html
Опосля компилируем программу командой make.

Для правильной работы программы нужно настроить звуковую карту. В Убунте это делается так: Система-> Параметры-> Звук. Выбираем микрофонный вход, выставляем громкость на максимум и снимаем галку «Выключить». Опционально, можно подключить к линейному входу звуковой карты радиоприёмник, тогда вместо микрофонного входа можно использовать линейный вход.
Одно замечание — микрофон должен быть отключен от входа звуковой карты. Говорят, что бросать микрофонный вход не стоит, так что в принципе можно зашунтировать (для желающих) его сопротивлением равным сопротивлению микрофона.

Итак, запускаем программу «./sound_distribution» и любуемся спустя 3-4 секунды результатом.

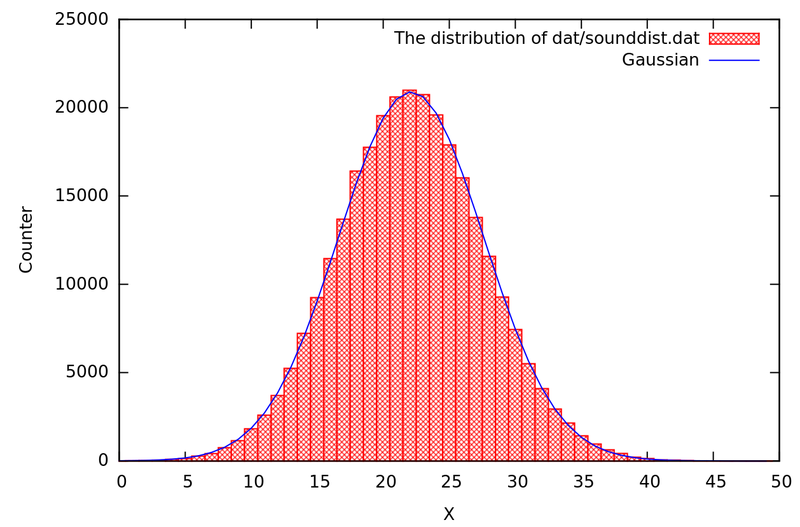
Гистограмма полученных значений

Осциллограмма получаемых значений с микрофонного входа.

Гистограмма получилась столь удачной, что её можно вставить в качестве иллюстрации в любой учебник по терверу, хотя это совершенно эмпирические значения.

Применение на практике

Как я уже описал, для программиста нужны числа, имеющие равномерное распределение. В данном случае у нас распределение нормальное, где число колеблется вокруг математического ожидания. Чтобы получать числа, необходимые нам, надо брать младшие четыре бита числа. Эти четыре бита будут принимать совершенно случайное значение. И эти четыре бита укладывать в число необходимой длинны. Например, для того чтобы заполнить число типа short (2 байта), нам понадобится 4 числа снятых со звуковой карты, а точнее их младшие разряды. Вот пример кода:

Домашним заданием будет сделать так, чтобы число можно было генерировать в заданном диапазоне и для разных типов данных. Ну и так же построение распределения для этих случайных чисел :).

Планы на будущее

На будущее я хотел сделать программу на GTK+, чтобы можно было ползунками изменять ширину интервалов, частоту дискретизации, количество получаемых данных, входные данные и т. п. Но увы, обломал пока зубы. Сделал только график осциллограммы получаемого сигнала, склепав его из нескольких программ. В этом вопросе я буду очень признателен за посильную помощь.
Как вариант, можно поставить стационарный приёмник, поставить вторую звуковую карту, чисто для генератора случайных чисел. Написать демон или драйвер, которые бы имели некий файл случайных данных, наподобии /dev/random, из которого можно читать данные. В общем, применений масса.

Примечания и выводы

Надо сказать, что генерация случайных чисел таким способом относительно медленная. Его тормозит скорость чтения данных со звуковой карты. Но в некоторых, не критичных к скорости выполнения, задачах, будет самое оно.

На самом деле, получение случайных чисел со звуковой карты явилось побочные продуктом, моего личного небольшого исследования, и в данном случае, служит мне только для обкатки моих скромных алгоритмов и визуализации данных.

Моя программа сохраняет три файла:
array.dat – Это просто сырые данные снятого массива
error.log – этот файл предполагался (как видно из названия) для сохранения ошибок, но пока используется для сохранения упорядоченного массива. Который в общем-то и служил мне для отладки.
sounddist.dat – Сам файл выходных данных. В первом столбце порядковый номер столба диаграммы, второй столбец– значение относительных частот, третий – распределение Гаусса, рассчитанное по стандартной формуле, четвёртый – диапазон значений, которые попадают в данный столбец диаграммы.

Я не знаю почему, но в этой программе перестали работать #define. Попытка инициализировать переменную с помощью define приводят к ошибке. Как, например, если заменить: «arg = 16;» (строка 83) на «arg = SIZE;» (закоменнтировать строку 83 и раскомментрировать строку 79), то компилятор выдаст ошибку:

sound_distribution.c: In function ‘main’:
sound_distribution.c:81: error: stray ‘\321’ in program
sound_distribution.c:81: error: stray ‘\216’ in program
make: *** [sound_distribution] Ошибка 1

Самое забавное, что в оригинальной программе инициализация переменных идёт именно через дефайны. Отсутствие дефайнов делает код не очень удобным для правки, но беглое гугление не дало ответ на эту проблему.

Ошибка найдена и исправлена, спасибо galaxy

В качестве вывода хочу сказать, что аппаратный генератор случайных чисел получить очень просто, достаточно только оглянуться вокруг :).

Я буду признателен любой конструктивной критикие, начиная от стилистики написания программ, заканчивая алгоритмами. Так же буду признателен за любую посильную помощь в продлжении проекта на GTK+.

Так же хочу сказать, что данный пост не последний по этой теме.

Список используемой литературы

Добавляются:
6. Н.С. Маркин «Основы теории обработки результатов измерения»
7. habrahabr.ru/blogs/python/62237 Случайные числа из звуковой карты

Список литературы будет ещё дополняться и расширяться, поскольку сейчас под рукой нет всех тех книг, которые я использовал при написании программы, понимании тервера и написании этого поста.

Эффективная генерация числа в заданном интервале

В подавляющем большинстве моих постов о генерации случайных чисел рассматривались в основном свойства различных схем генерации. Это может оказаться неожиданным, но производительность алгоритма рандомизации может зависеть не от выбранной схемы генерации, а от других факторов. В этом посте (на который меня вдохновила превосходная статья Дэниела Лемира) мы исследуем основные причины снижения производительности генерации случайных чисел, которые часто перевешивают производительность движка ГПСЧ.

Представьте такую ситуацию:

В качестве домашнего задания Хуан и Саша реализуют одинаковый рандомизированный алгоритм на C++, который будет выполняться на одном университетском компьютере и с одним набором данных. Их код почти идентичен и отличается только в генерации случайных чисел. Хуан торопится на свои занятия по музыке, поэтому просто выбрал вихрь Мерсенна. Саша, с другой стороны, потратил несколько лишних часов на исследования. Саша провёл бенчмарки нескольких самых быстрых ГПСЧ, о которых недавно узнал из соцсетей, и выбрал наиболее быстрый. При встрече Саше не терпелось похвастаться, и он спросил Хуана: «Какой ГПСЧ ты использовал?»

«Лично я просто взял вихрь Мерсенна — он встроен в язык и вроде неплохо работает».

«Хм, неплохо, а моя справляется меньше, чем за минуту», — говорит Хуан и пожимает плечами. «Ну ладно, мне пора на концерт. Пойдёшь со мной?»

«Нет», — отвечает Саша. «Мне… эээ… нужно снова взглянуть на свой код».

Эта неловкая вымышленная ситуация не особо и вымышлена; она основана на реальных результатах. Если ваш рандомизированный алгоритм выполняется не так быстро, как хотелось бы, и узким местом похоже является генерация случайных чисел, то, как это ни странно, проблема может быть и не в генераторе случайных чисел!

Введение: случайные числа на практике

Большинство современных качественных генераторов случайных чисел создаёт машинные слова, заполненные случайными битами, то есть обычно генерирует числа в интервале [0..2 32 ) или [0..2 64 ). Но во многих случаях использования пользователям нужны числа в определённом интервале — например, для броска кубика или выбора случайной игральной карты нужны числа в небольших постоянных интервалах. Однако многим алгоритмам, от перемешивания и reservoir sampling до рандомизированных двоичных деревьев поиска требуются числа, берущиеся из других интервалов.

Методы

Мы рассмотрим множество различных методов. Чтобы упростить обсуждение, вместо генерации чисел в интервале [i..j) или [i..j] мы будем генерировать числа в интервале [0..k). Имея такую схему, мы сможем, например, генерировать числа в интервале [i..j), задав k = j — i, сгенерировав число в интервале [0..k), а затем прибавив к нему i.

Встроенные средства C++

Код на C++ для реализации такого подхода прост:

Классический остаток от деления (с перекосом)

Давайте перейдём от переусложнённого подхода к слишком упрощённому.

На C++ такой подход можно реализовать следующим образом:

Несмотря на простоту такого подхода, он демонстрирует причину того, что получение чисел в нужном интервале обычно является медленной задачей — для него требуется деление (чтобы вычислить остаток, получаемый оператором % ). Деление обычно как минимум на порядок величин медленнее, чем другие арифметические операции, поэтому единственная арифметическая операция занимает больше времени, чем вся работа, выполняемая быстрым ГПСЧ.

В этой статье мы в основном будем рассматривать методики, в которых используются стратегии для устранения систематической ошибки, но наверно стоит сказать, что для 64-битного ГПСЧ величина перекоса в обычных случаях применения скорее всего будет ничтожной.

Ещё одна проблема может заключаться в том, что некоторые генераторы имеют слабые младшие биты. Например, семейства ГПСЧ Xoroshiro+ и Xoshiro+ имеют младшие биты, которые не проходят статистических тестов. Когда мы выполняем % 52 (потому что 52 чётное), то передаём младший бит прямиком на выход.

Умножение чисел с плавающей запятой (с перекосом)

Ещё одна распространённая методика — использование ГПСЧ, генерирующего числа с плавающей запятой в интервале [0..1) с последующим преобразованием этих чисел в нужный интервал. Такой подход применяется в Perl, в нём рекомендуется использовать int(rand(10)) для генерации целого числа в интервале [0..10) генерацией числа с плавающей запятой с последующим округлением вниз.

На C++ этот подход записывается так:

Этот подход столь же перекошен, как и классический остаток от деления, но перекос проявляется иначе. Например, если бы мы выбирали числа в интервале [0..52), то числа 0, 13, 26 и 39 встречались бы на один раз реже, чем другие.

Есть и хорошая сторона — этот подход работает быстрее, чем решения на основе остатков для ГПСЧ со слабыми младшими битами.

Целочисленное умножение (с перекосом)

Может показаться, что для этой версии требуется 64-битная арифметика, на процессорах x86 хороший компилятор скомпилирует этот код в 32-битную инструкцию mult (которая даёт нам два 32-битных выходных значения, одно из которых является возвращаемым значением). Можно ожидать, что эта версия будет быстрой, но она перекошена точно так же, как метод умножения чисел с плавающей запятой.

Деление с отбрасыванием (без перекоса)

Например, в случае вытаскивания карты с помощью 32-битного ГПСЧ мы можем сгенерировать 32-битное число и разделить его на 2 32 /52 = 82 595 524, чтобы выбрать карту. Эта методика работает, если случайное значение из 32-битного ГПСЧ меньше 52 × 82595524 = 2 32 /32 – 48. Если случайное значение из ГПСЧ является одним из последних 48 значений верхней части интервала генератора, то его нужно отбросить и искать другое.

Следовательно, код на C++ для генерации чисел с помощью деления с отбрасыванием выглядит так:

Разумеется, такой подход требует двух медленных операций на основе деления, которые обычно медленнее, чем другие арифметические операции, поэтому не стоит ожидать, что он будет быстрым.

Остаток от деления (двойной) без перекосов — методика OpenBSD

Мы также можем применить подход с отбрасыванием для устранения перекоса в классическом методе остатка от деления. В примере с игральными картами нам снова нужно отбросить 48 значения. В этой версии вместо отбрасывания последних 48 значений мы (эквивалентно) отбрасываем первые 48 значений.

Вот реализация этого подхода на C++:

Эта техника устраняет перекос, но для неё требуется две затратные по времени операций деления с остатком на каждое выходное значение (и может потребоваться внутренний генератор для создания нескольких чисел). Следовательно, стоит ожидать, что способ будет примерно в два раза медленнее классического подхода с перекосом.

В коде arc4random_uniform OpenBSD (который также используется в OS X и iOS) применяется эта стратегия.

Остаток от деления (одиночный) без перекоса — методика Java

В Java используется другой подход к генерации числа в интервале, в котором используется только одна операция деления с остатком, за исключением довольно редких случаев отбрасывания результата. Код:

Чтобы понять, почему этот вариант работает, нужно немного подумать. В отличие от предыдущей версии, основанной на остатках, которая устраняет перекос удалением части самых низких значений из внутреннего движка генерации, эта версия отфильтровывает значения из верхней части интервала движка.

Целочисленное умножение без перекосов — методика Лемира

Почти так же, как мы устранили перекос из методики остатка от деления, мы можем устранить перекос из методики целочисленного умножения. Эта методика была придумана Лемиром.

Битовая маска с отбрасыванием (без перекосов) — методика Apple

В нашем последнем подходе полностью исключаются операции деления и остатка. Вместо них в нём используется простая операция маскирования для получения случайного числа в интервале [0..2 k ), где k — наименьшее значение, такое, что 2 k больше интервала. Если значение слишком велико для нашего интервала, мы отбрасываем его и пробуем получить другое. Код показан ниже:

Бенчмаркинг базовых методик

Теперь у нас есть несколько подходов, которые можно оценить. К сожалению, когда нас беспокоят затраты на одну операцию деления, бенчмаркинг становится нетривиальным делом. Никакой бенчмарк не способен учесть все факторы, влияющие на область применения, и нет никаких гарантий, что наилучший вариант для вашего приложения обязательно будет лучшим для моего.

Мы используем три бенчмарка и протестируем методики со множеством различных ГПСЧ.

Бенчмарк Large-Shuffle

Заметьте, что мы «используем» каждое число, прибавляя его к sum (чтобы его не отбросила оптимизация), но не выполняем никакого перемешивания, чтобы сосредоточиться на генерации чисел.

Для тестирования 64-битной генерации у нас есть аналогичный тест, но будет непрактично выполнять тест, соответствующий перемешиванию массива размером 2 64 – 1 (потому что на выполнение этого более масштабного бенчмарка потребуется много тысяч лет). Вместо этого мы пересечём весь 64-битный интервал, но сгенерируем то же количество выходных значений, что и в 32-битном тесте. Код:

Результаты вихря Мерсенна

Показанные ниже результаты демонстрируют производительность этого бенчмарка для каждого из рассмотренных нами методов при использовании вихря Мерсенна и тестировании на рассмотренном в статье 32-битном (при помощи std::mt19937 из libstdc++ ) и аналогичном 64-битном коде (при помощи std:mt19937_64 из libstdc++ ). Результаты — это геометрическое среднее 15 прогонов с разными значениями seed, которое затем нормализовано, чтобы классический метод остатка от деления имел единичное время выполнения.

Результаты разных ГПСЧ

Мы можем увидеть ключевые отличия от результатов с вихрем Мерсенна. Более быстрые ГПСЧ сдвигают равновесие в сторону ограничивающего кода, а потому разница между разными подходами становится более явной, особенно в случае 64-битных ГПСЧ. При более широком наборе ГПСЧ реализация libstc++ перестаёт казаться такой ужасной.

Выводы

В этом бенчмарке со значительным отрывом выигрывает в скорости подход на основе умножения с перекосом. Есть множество ситуаций, в которых границы будут маленькими относительно размера ГПСЧ, а производительность абсолютно критична. В таких ситуациях незначительный перекос скорее всего не окажет заметного влияния, зато скорость ГПСЧ окажет. Одним из таких примеров является Quicksort со случайной опорной точкой. Из методов без перекосов многообещающей выглядит техника битовых масок.

Но прежде чем делать серьёзные выводы, нам нужно указать на огромную проблему этого бенчмарка — основная часть времени тратится на очень высокие границы, что скорее всего придаёт чрезмерное значение большим интервалам. Следовательно, нам нужно перейти ко второму бенчмарку.

Бенчмарк Small-Shuffle

Этот бенчмарк похож на предыдущий, но выполняет гораздо меньшее «перемешивание массива» (многократное). Код:

Результаты вихря Мерсенна

Результаты разных ГПСЧ

Выводы

Этот бенчмарк избегает слишком большого упора на большие границы и более точно отражает реальные случаи применения, но теперь полностью отбрасывает большие границы.

Бенчмарк для всех интервалов

Этот бенчмарк направлен на то, чтобы избежать недостатков предыдущих двух; он выполняет тестирование при каждом размере степени двойки, чтобы присутствовал каждый размер, но его влияние не переоценивалось.

Результаты вихря Мерсенна

Результаты разных ГПСЧ

Выводы

Многие из наших выводов остаются неизменными. Метод умножения с перекосом быстр, если мы можем смириться с погрешностью, а схема с битовой маской, похоже, является хорошим усреднённым выбором.

На этом мы могли бы завершить, если бы не захотели вернуться обратно, критически взглянуть на свой код и внести в него изменения.

Вносим улучшения

До этого момента все методы устранения перекоса требовали использования дополнительной операции остатка деления, из-за чего они выполняются гораздо медленнее, чем методы с перекосом. Было бы полезно, если бы мы смогли снизить этот перевес.

Более быстрое отбрасывание на основе порогов

В некоторых наших алгоритмах есть код с использованием порогового значения, например:

Когда range мал по сравнению с выходным интервалом ГПСЧ, чаще всего число будет намного больше порога. То есть если мы сможем добавить предварительную оценку порога, который может быть немного больше, то сэкономим на затратной операции взятия остатка деления.

С этой задачей справляется такой код:

Это изменение можно применить и к «двойному Mod без перекосов» (см. выше), и к «целочисленному умножению без перекосов». Идею придумал Лемир, который применил её ко второму методу (но не к первому).

Результаты бенчмарка Large-Shuffle

Эта оптимизация приводит к значительному улучшению результатов 64-битного бенчмарка (в котором mod даже медленнее), но на самом деле слегка ухудшает производительность в 32-битном бенчмарке. Несмотря на усовершенствования, метод с битовой маской всё равно побеждает.

Результаты бенчмарка Small-Shuffle

С другой стороны, это изменение значительно ускоряет бенчмарк small-shuffle и для метода умножения целых чисел, и для метода двойного остатка от деления. В обоих случаях их производительность сдвигается ближе к результатам вариантов без перекосов. Производительность метода двойного остатка (OpenBSD) теперь почти равна показателям метода одиночного остатка (Java).

Результаты бенчмарков для всех интервалов

Похожее улучшение мы видим и в бенчмарке для всех интервалов.

Похоже, что мы можем объявить нового всеобщего победителя: оптимизированный метод умножения целых чисел Лемира без перекосов.

Оптимизация остатка от деления

мы можем выполнить

Затратность деления настолько значительна, что повышение расходов на этот более сложный код может оправдать себя экономией времени благодаря отсутствию деления.

Результаты бенчмарка Large-Shuffle

Добавление этой оптимизации значительно улучшает результаты бенчмарка large-shuffle. Это снова более заметно в 64-битном коде, где операция взятия остатка затратнее. В методе с двойным остатком (в стиле OpenBSD) показаны версии с оптимизацией только для одной операции остатка и для обеих.

В этом бенчмарке битовая маска по-прежнему остаётся победителем, но граница между нею и подходом Лемира значительно сузилась.

Результаты бенчмарка Small-Shuffle

Добавление этой оптимизации не повышает производительность бенчмарка small-shuffle, поэтому вопрос остаётся только в том, добавляет ли он значительные затраты. В некоторых случаях нет, в других затраты увеличиваются незначительно.

Результаты бенчмарка для всех интервалов

В бенчмарке для всех интервалов изменения тоже малы.

Бонус: результаты сравнения ГПСЧ

Основная причина использования множества ГПСЧ для тестирования схем чисел в интервалах заключалась в том, чтобы избежать непреднамеренного искажения результатов вследствие особенностей работы отдельных схем ГПСЧ. Но мы можем использовать те же результаты внутренних тестов и для сравнения самих схем генерации.

ГПСЧ с выводом 32-битных чисел

График ниже показывает производительность разных 32-битных схем генерации, усреднённых для всех методов и пятнадцати прогонов, нормализованные по производительности 32-битного вихря Мерсенна:

С одной стороны, я рад видеть, что pcg32_fast и в самом деле быстр — его победил только небольшой вариант Xoroshiro (который не проходит статистические тесты). Но это показывает и то, почему я редко расстраиваюсь из-за производительности современных высокопроизводительных ГПСЧ общего назначения — разница между разными методами очень незначительна. В частности, самые быстрые четыре схемы отличаются по производительности меньше чем на 5%, и я считаю, что это просто вызвано «шумом».

ГПСЧ с выводом 64-битных чисел

На графике показана производительность разных 64-битных схем генерации, усреднённых среди всех техник и пятнадцати прогонов, нормализованных по производительности 32-битного вихря Мерсенна. Может показаться странным, что нормализация выполняется по 32-битному вихрю Мерсенна, но это позволяет нам увидеть дополнительные затраты от использования 64-битной генерации в случаях, когда достаточно 32-битной генерации.

Но возможно более важно то, что эти результаты также показывают, что если вам не нужен 64-битный вывод, то 64-битный ГПСЧ обычно медленнее, чем 32-битный.

Выводы

Из наших бенчмарков мы можем увидеть, что переход от стандартно используемых ГПСЧ (например, 32-битного вихря Мерсенна) к более быстрым ГПСЧ снизило время выполнения бенчмарков на 45%. Но переход от стандартного метода поиска числа в интервале к нашему самому быстрому методу позволило снизить время бенчмарка примерно на 66%; другими словами, до одной трети от исходного времени.

Самый быстрый метод (без перекосов) — это метод Лемира (с моей дополнительной оптимизацией). Вот он:

Использование метода Лемира улучшит производительность большинства рандомизированных алгоритмов больше, чем переход от быстрого движка генерации к работающему немного быстрее.

Приложения: примечания по тестированию

Код всех тестов выложен на GitHub. В целом я протестировал 23 метода для bounded_rand с помощью 26 разных ГПСЧ (13 32-битных ГПСЧ и 13 64-битных), в двух компиляторах (GCC 8 и LLVM 6), что дало мне 26 * 23 * 2 = 1196 исполняемых файлов, каждый из которых выполнялся с одинаковыми 15 seed, что даёт 1196 * 15 = 17 940 уникальных прогонов тестов, в каждом из которых объединено три бенчмарка. В основном я прогонял тесты на 48-ядерной машине с четырьмя процессорами Xeon E7-4830v3 с частотой 2,1 ГГц. Выполнение полного набора тестов потребовало чуть меньше месяца процессорного времени.