Как из синуса сделать косинус
Как из синуса сделать косинус
Формулы перехода от синуса к косинусу
Определения синуса, косинуса, тангенса и котангенса.
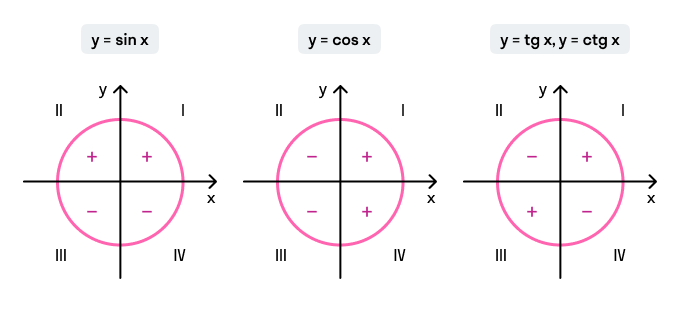
Знаки тригонометрических функций:
Значения тригонометрических функций
Формулы синуса, косинуса, тангенса и котангенса угла (–α):
sin (–α) = – sin α
cos (–α) = cos α
tg (–α) = – tg α
ctg (–α) = – ctg α
Все формулы приведения можно получить, пользуясь следующими правилами:
1. В правой части формулы ставится тот знак, который имеет левая часть при условии
2. Если в левой части формулы угол равен 







Формулы двойного угла.
Формулы перехода от суммы к произведению.
Формулы перехода от произведения к сумме.
Формулы понижения степени.
Преобразование выражения a·cos 


где вспомогательный аргумент определяется из условий
Основные формулы тригонометрии – это формулы, устанавливающие связи между основными тригонометрическими функциями. Синус, косинус, тангенс и котангенс связаны между собой множеством соотношений. Ниже приведем основные тригонометрические формулы, а для удобства сгруппируем их по назначению. С использованием данных формул можно решить практически любую задачу из стандартного курса тригонометрии. Сразу отметим, что ниже приведены лишь сами формулы, а не их вывод, которому будут посвящены отдельные статьи.
Основные тождества тригонометрии
Тригонометрические тождества дают связь между синусом, косинусом, тангенсом и котангенсом одного угла, позволяя выразить одну функцию через другую.
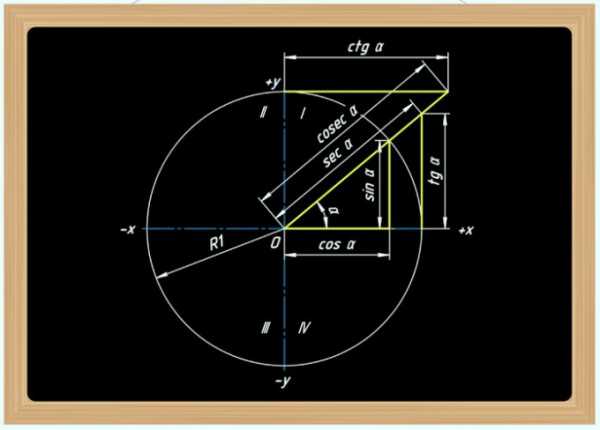
Эти тождества напрямую вытекают из определений единичной окружности, синуса (sin), косинуса (cos), тангенса (tg) и котангенса (ctg).
Формулы приведения
Формулы приведения позволяют переходить от работы с произвольными и сколь угодно большими углами к работе с углами в пределах от 0 до 90 градусов.
Формулы приведения являются следствием периодичности тригонометрических функций.
Тригонометрические формулы сложения
Формулы сложения в тригонометрии позволяют выразить тригонометрическую функцию суммы или разности углов через тригонометрические функции этих углов.
Тригонометрические формулы сложения
sin α ± β = sin α · cos β ± cos α · sin β cos α + β = cos α · cos β – sin α · sin β cos α – β = cos α · cos β + sin α · sin β t g α ± β = t g α ± t g β 1 ± t g α · t g β c t g α ± β = – 1 ± c t g α · c t g β c t g α ± c t g β
На основе формул сложения выводятся тригонометрические формулы кратного угла.
Формулы кратного угла: двойного, тройного и т.д.
Формулы половинного угла
Формулы половинного угла в тригонометрии являются следствием формул двойного угла и выражают соотношения между основными функциями половинного угла и косинусом целого угла.
Формулы половинного угла
sin 2 α 2 = 1 – cos α 2 cos 2 α 2 = 1 + cos α 2 t g 2 α 2 = 1 – cos α 1 + cos α c t g 2 α 2 = 1 + cos α 1 – cos α
Формулы понижения степени
sin 2 α = 1 – cos 2 α 2 cos 2 α = 1 + cos 2 α 2 sin 3 α = 3 sin α – sin 3 α 4 cos 3 α = 3 cos α + cos 3 α 4 sin 4 α = 3 – 4 cos 2 α + cos 4 α 8 cos 4 α = 3 + 4 cos 2 α + cos 4 α 8
Часто при расчетах действовать с громоздктми степенями неудобно. Формулы понижения степени позволяют понизить степень тригонометрической функции со сколь угодно большой до первой. Приведем их общий вид:
Общий вид формул понижения степени
sin n α = C n 2 n 2 n + 1 2 n – 1 ∑ k = 0 n 2 – 1 ( – 1 ) n 2 – k · C k n · cos ( ( n – 2 k ) α ) cos n α = C n 2 n 2 n + 1 2 n – 1 ∑ k = 0 n 2 – 1 C k n · cos ( ( n – 2 k ) α )
sin n α = 1 2 n – 1 ∑ k = 0 n – 1 2 ( – 1 ) n – 1 2 – k · C k n · sin ( ( n – 2 k ) α ) cos n α = 1 2 n – 1 ∑ k = 0 n – 1 2 C k n · cos ( ( n – 2 k ) α )
Сумма и разность тригонометрических функций
Разность и сумму тригонометрических функций можно представить в виде произведения. Разложение на множители разностей синусов и косинусов очень удобно применять при решении тригонометрических уравнений и упрощении выражений.
Сумма и разность тригонометрических функций
Произведение тригонометрических функций
Если формулы суммы и разности функций позволяют перейти к их произведению, то формулы произведения тригонометрических функций осуществляют обратный переход – от произведения к сумме. Рассматриваются формулы произведения синусов, косинусов и синуса на косинус.
Формулы произведения тригонометрических функций
sin α · sin β = 1 2 · ( cos ( α – β ) – cos ( α + β ) ) cos α · cos β = 1 2 · ( cos ( α – β ) + cos ( α + β ) ) sin α · cos β = 1 2 · ( sin ( α – β ) + sin ( α + β ) )
Универсальная тригонометрическая подстановка
Все основные тригонометрические функции – синус, косинус, тангенс и котангенс, – могут быть выражены через тангенс половинного угла.
Универсальная тригонометрическая подстановка
sin α = 2 t g α 2 1 + t g 2 α 2 cos α = 1 – t g 2 α 2 1 + t g 2 α 2 t g α = 2 t g α 2 1 – t g 2 α 2 c t g α = 1 – t g 2 α 2 2 t g α 2
Тригонометрические формулы
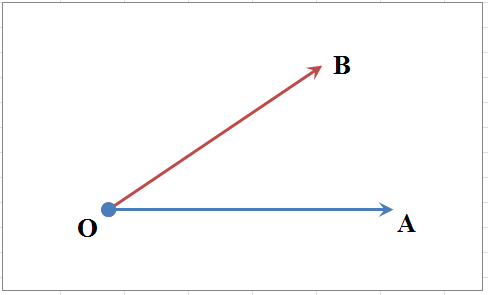
Тригонометрические формулы основаны на тригонометрических функциях (ТФ) углов.
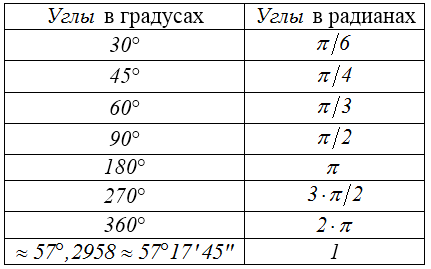
Распространены две системы измерения углов: градусная и радианная.
Попробуй обратиться за помощью к преподавателям
Полезно помнить следующую таблицу градусной и радианной меры некоторых часто встречающихся углов:
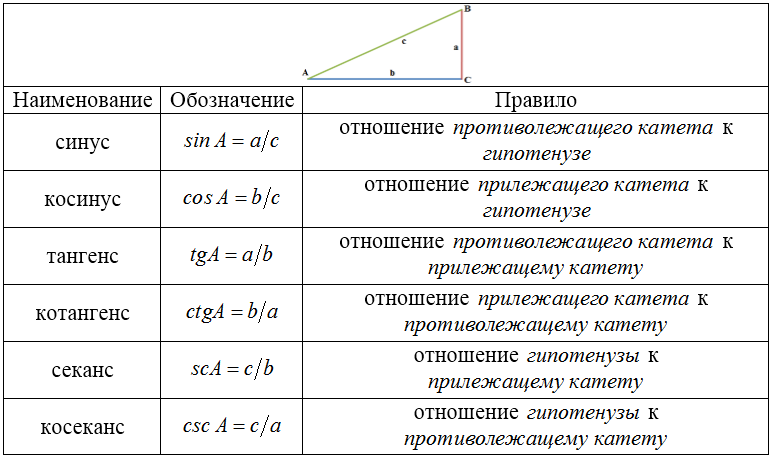
Определение синуса, косинуса и тангенса, знаки синуса, косинуса и тангенса
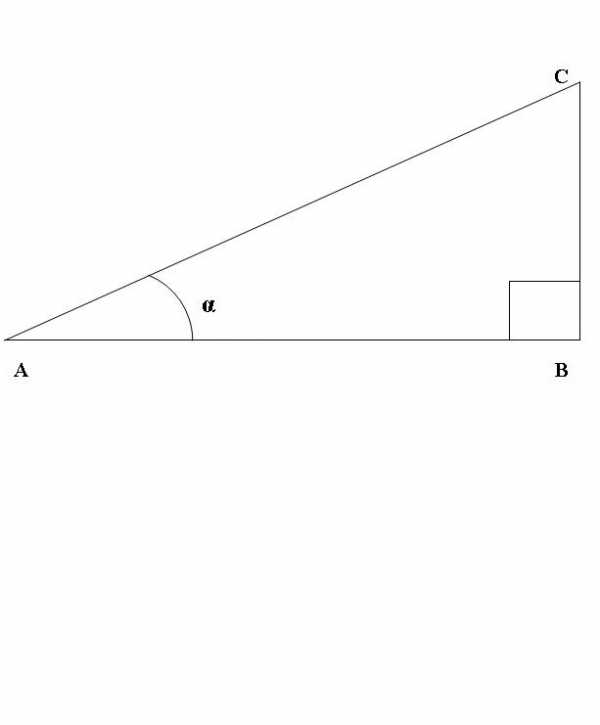
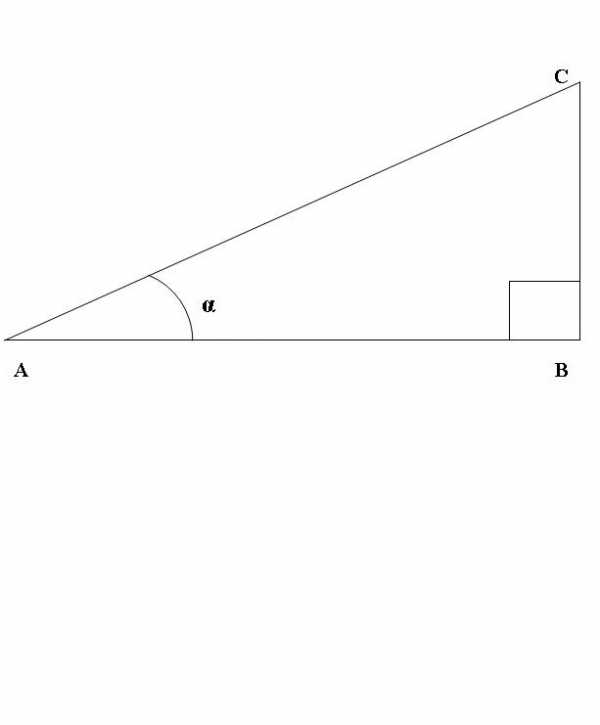
ТФ острого угла можно определить из прямоугольного треугольника:
Задай вопрос специалистам и получи
ответ уже через 15 минут!
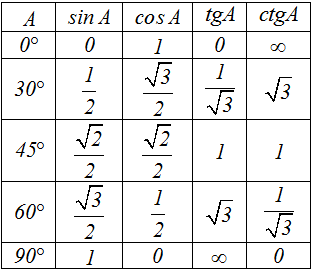
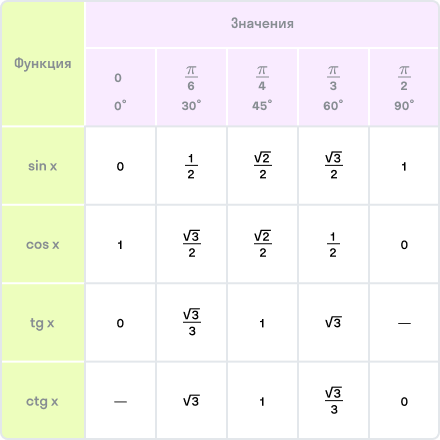
Полезно помнить значения основных ТФ для часто встречающихся значений углов:
Обратные тригонометрические функции (ОТФ)
ОТФ многозначны. Поэтому из всего множества значений каждой из них выделяют главные, а наименования указывают со строчной буквы:
Тригонометрические формулы. Их вывод
Наиболее часто встречающиеся тригонометрические формулы:
\(\blacktriangleright\) Основные тождества: \[\begin
\(\blacktriangleright\) Формулы сложения углов: \[\begin
\(\blacktriangleright\) Формулы понижения степени: \[\begin
\(\blacktriangleright\) Формулы произведения функций: \[\begin
\(\blacktriangleright\) Выражение синуса и косинуса через тангенс половинного угла: \[\begin
\(\blacktriangleright\) Формула вспомогательного аргумента: \[\begin
Зная идею вывода формул, вы можете запомнить лишь несколько из них. Тогда остальные формулы вы всегда сможете быстро вывести.
Вывод всех основных тождеств был рассказан в предыдущем разделе “Введение в тригонометрию”.
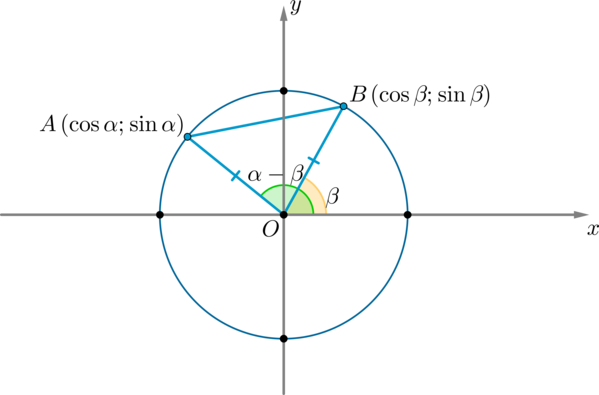
\(AB^2=AO^2+BO^2-2AO\cdot BO\cdot \cos(\alpha-\beta)=1+1-2\cos(\alpha-\beta) \ (1)\) (т.к. \(AO=BO=R\) – радиус окружности)
По формуле расстояния между двумя точками на плоскости:
Таким образом, сравнивая равенства \((1)\) и \((2)\) :
Отсюда и получается наша формула.
\(\blacktriangleright\) Вывод остальных формул суммы/разности углов:
Остальные формулы с легкостью выводятся с помощью предыдущей формулы, свойств четности/нечетности косинуса/синуса и формул приведения \(\sin x=\cos(90^\circ-x)\) и \(\cos x=\sin (90^\circ-x)\) :
\(\blacktriangleright\) Вывод формул двойного и тройного углов:
Данные формулы выводятся с помощью предыдущих формул:
1) \(\sin 2\alpha=\sin(\alpha+\alpha)=\sin\alpha\cos\alpha+\sin\alpha\cos\alpha=2\sin\alpha\cos\alpha\)
разделим числитель и знаменатель дроби на \(\cos^2\alpha\ne 0\) (при \(\cos\alpha=0 \Rightarrow \mathrm
5) \(\sin3\alpha=\sin(\alpha+2\alpha)=\sin\alpha\cos2\alpha+\cos\alpha\sin2\alpha=\sin\alpha(1-2\sin^2\alpha)+\cos\alpha\cdot 2\sin\alpha\cos\alpha=\)
6) Аналогично выводится, что \(\cos3\alpha=\cos(\alpha+2\alpha)=4\cos^3\alpha-3\cos\alpha\)
\(\blacktriangleright\) Вывод формул понижения степени:
Данные формулы — просто по-другому записанные формулы двойного угла для косинуса:
1) \(\cos2\alpha=2\cos^2\alpha-1 \Rightarrow \cos^2\alpha=\dfrac<1+\cos2\alpha>2\)
2) \(\cos2\alpha=1-2\sin^2\alpha \Rightarrow \sin^2\alpha=\dfrac<1-\cos2\alpha>2\)
\(\blacktriangleright\) Вывод формул произведения функций:
1) Сложим формулы косинуса суммы и косинуса разности двух углов:
Получим: \(\cos(\alpha+\beta)+\cos(\alpha-\beta)=2\cos\alpha\cos\beta \Rightarrow \cos\alpha\cos\beta=\dfrac12\Big(\cos(\alpha-\beta)+\cos(\alpha+\beta)\Big)\)
2) Если вычесть из формулы косинуса суммы косинус разности, то получим:
3) Сложим формулы синуса суммы и синуса разности двух углов:
\(\blacktriangleright\) Вывод формул суммы/разности функций:
Получили формулу суммы косинусов.
Получили формулу разности косинусов.
Получили формулу суммы синусов.
4) Формулу разности синусов можно вывести из формулы суммы синусов:
Аналогично выводится формула суммы котангенсов.
\(\blacktriangleright\) Вывод формул выражения синуса и косинуса через тангенс половинного угла:
(разделим числитель и знаменатель дроби на \(\cos^2\alpha\ne 0\) (при \(\cos\alpha=0\) и \(\sin2\alpha=0\) ):)
\(\blacktriangleright\) Вывод формул вспомогательного угла:
Данные формулы выводятся с помощью формул синуса/косинуса суммы/разности углов.
\(a\sin x+b\cos x=\sqrt
\(\sqrt
Значит, формула выглядит следующим образом: \[<\large
\(\blacktriangleright\) Рассмотрим некоторые частные случаи формул вспомогательного угла:
\(a) \ \sin x\pm\cos x=\sqrt2\,\left(\dfrac1<\sqrt2>\sin x\pm\dfrac1<\sqrt2>\cos x\right)=\sqrt2\, \sin \left(x\pm\dfrac<\pi>4\right)\)
\(b) \ \sqrt3\sin x\pm\cos x=2\left(\dfrac<\sqrt3>2\sin x\pm \dfrac12\cos x\right)=2\, \sin \left(x\pm\dfrac<\pi>6\right)\)
\(c) \ \sin x\pm\sqrt3\cos x=2\left(\dfrac12\sin x\pm\dfrac<\sqrt3>2\cos x\right)=2\,\sin\left(x\pm\dfrac<\pi>3\right)\)
Формулы связи тригонометрических функций. Примеры из ЕГЭ
\(sin^2 776^° +cos^2 776^° =1\)
\(tg\, 3x\cdot ctg\, 3x=1\)
\(sin^2x+cos^23x≠1\)
\(tg\, x\cdot ctg\, y≠1\)
Примеры применения формул связи
Пример. Найдите \(5sin\,α\), если \(cos\,α=\frac<2\sqrt<6>><5>\) и \(α∈(\frac<3π><2>;2π)\).
Решение. Нам известен косинус, найти надо синус. А что связывает синус и косинус? Основное тригонометрическое тождество:
Подставим вместо косинуса его значение:
Внимание! Последняя строчка – место, где теряется огромное количество баллов на ЕГЭ! Это одна из самых популярных ошибок – забыть отрицательный корень. Пожалуйста, раз и навсегда запомните, что у неполного квадратного уравнения вида \(x^2=a\) (при \(a>0\)) два корня \(x_1=\sqrt\) и \(x_2=-\sqrt\). Пусть двойка над иксом (та которая «квадрат») будет вам вечным маяком, сигнализирующим: «тут ДВА корня! Два! Не забудь!»
Обратите внимание – в этой четверти синус принимает только отрицательные значения (можно провести перпендикуляры до оси синусов и убедиться, что это так).
Значит, в нашем случае \(sin\,α=-\frac<1><5>\) т.е. \(5sin\,α=5\cdot(-\frac<1><5>)=-1\).
Пример.Найдите \(tg\,α\), если \(cos\,α=\) \(\frac<\sqrt<10>><10>\) и \(α∈(\frac<3π><2>;2π)\).
Решение. Есть 2 пути решения этой задачи:
— напрямую вычислить тангенс через формулу \(tg^2α+1=\) \(\frac<1>
— сначала с помощью тождества \(sin^2α+cos^2α=1\) найти \(sin\,α\), а потом через формулу \(tg\,α=\) \(\frac
В учебниках обычно идут первым путем, поэтому мы пойдем вторым.
Теперь вычислим косинус по упомянутой выше формуле:
Опять перед нами стоит выбор плюс или минус. Отметим отрезок \((\frac<π><2>;π)\) на тригонометрической окружности и посмотрим какие значения принимает косинус в этой четверти, чтобы определится со знаком.
Осталось найти синус:
Опять используем круг, чтобы определить знак.
Пример (ЕГЭ). Найдите \(tg^2 α\), если \(5 sin^2α+13 cos^2α=6\).
Решение. Давайте пойдем от того, что известно. В равенстве \(5 sin^2α+13 cos^2α=6\) синус заменим на косинус:
Поняли почему именно синус заменили на косинус, а не наоборот? И почему не надо извлекать корень, досчитывая до «чистого» косинуса? Потому что для нахождения \(tg^2α\) хорошо подходит формула \(tg^2α+1=\) \(\frac<1>
Теперь еще одна задача из ЕГЭ, для наглядности мы ее решение оформили картинкой.
Самое очевидное, что можно сделать – это представить котангенс как отношение косинуса к синусу.
Приводим дроби к общему знаменателю.
\(1-cos^2α\) можно заменить на \(sin^2 α\).
Все формулы приведения
Вы наверняка помните значения тригонометрических функций основных аргументов:
Список формул приведения
Формулы приведения c опорной точкой (случай n = 1):
Формулы приведения c опорной точкой (случай n = 2):
Формулы приведения c опорной точкой (случай n = 3):
Формулы приведения c опорной точкой (случай n = 4):
Доказательство формул
Чтобы убедиться, что формулы рабочие, рассмотрим примеры доказательств нескольких из них.
Для этого нам нужно будет вспомнить формулы сложения для синуса и косинуса:
Формула приведения с синусом
По формуле синуса суммы представим левую часть выражения:
Вычислим и в получившемся выражении:
Формула приведения с косинусом
Рассмотрим также пример формулы приведения с косинусом и докажем ее:
Аналогично распишем левую часть по формуле косинуса суммы:
Формула приведения с тангенсом
Чтобы доказать формулу приведения с тангенсом, нужно вспомнить, что тангенс — это отношение синуса к косинусу. Тогда для доказательства нужно лишь дважды использовать формулы сложения — попробуйте сами на формуле и сравните с примером.
При желании таким образом вы сможете доказать справедливость всех формул.
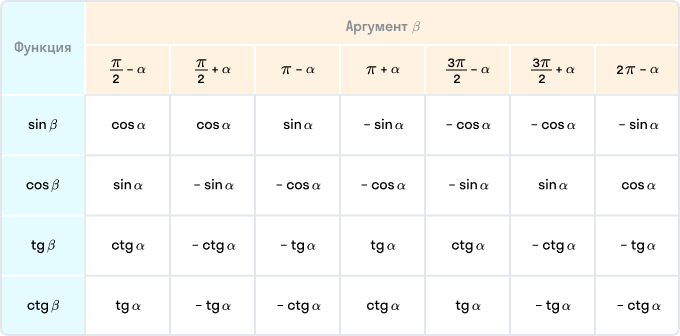
Таблица формул приведения
Нередко можно встретить такой вариант оформления формул приведения — в виде таблицы.
Для того чтобы воспользоваться этой таблицей, выберите строку с нужной функцией и столбец с необходимым аргументом — на их пересечении вы узнаете ответ.
Маленькую распечатанную таблицу формул приведения тригонометрических функций удобно иметь в пенале на случай неожиданных контрольных.
Как запомнить формулы приведения
Одно дело — воспользоваться формулами, а совсем другое — выучить их. Знать наизусть все формулы приведения или всю таблицу — дело нелегкое и, к счастью, абсолютно ненужное.
Поэтому познакомимся с мнемоническим алгоритмом:
Изобразите (на листе или мысленно) на единичной окружности данный угол.
С помощью окружности определите знак исходной функции. Полученная функция в правой части будет иметь такой же знак.
Напоминаю знаки тригонометрических функций во всех четвертях тригонометрической окружности:
Если в аргументе у опорной точки n — нечетное число, то исходную функцию замените на кофункцию, то есть на противоположную функцию (синус меняется на косинус, тангенс — на котангенс, и наоборот).
Если в аргументе у опорной точки n — четное число, то функция не меняется.
Вот с этим пунктом изменения или сохранения функции возникает постоянная путаница. А запомнить поможет «правило лошадки».
Таким образом, формулы приведения — это тригонометрические тождества вида
Задание 1
Найдите значение выражения
Вы видите, что каждое слагаемое выражения — это формула приведения тригонометрической функции. Упростим их по отдельности.
Далее изображаем данный угол на тригонометрической окружности:
Определяем знак исходной функции, то есть синуса. Синус этого угла принимает положительные значения.
В конце определяем, меняется ли функция. В этом нам поможет «правило лошадки»: опорная точка лежит на горизонтальной оси, значит, функция не меняется на кофункцию, то есть синус не меняется на косинус.
Приведем аналогичные рассуждения для всех слагаемых в выражении.
Косинус во второй четверти тригонометрической окружности принимает отрицательные значения.
Опорная точка лежит на вертикальной оси — это случай, когда косинус меняется на синус.
Косинус в третьей четверти тригонометрической окружности принимает отрицательные значения.
Опорная точка лежит на вертикальной оси — это случай, когда косинус меняется на синус.
А теперь запишем преобразованные выражения в наше исходное и упростим:
Обратите внимание, к какому простому виду удалось привести это сложное, на первый взгляд, выражение.
Задание 2
До этого момента мы говорили о формулах приведения тригонометрических функций углов, выраженных в радианах. Однако мы понимаем, что градусы и радианы — это разные способы представления одних и тех же углов или аргументов, поэтому тригонометрические формулы приведения работают и для выражений с градусами.
Так как первый шаг выполнен, то продолжаем идти по алгоритму.
Косинус в первой четверти тригонометрической окружности принимает положительные значения.
Опорная точка лежит на вертикальной оси, поэтому косинус меняется на синус.
Запишем преобразованные выражения в наше исходное и упростим:
Формулы приведения в тригонометрии занимают второе место по важности и частоте использования после основного тригонометрического тождества, так что осваивайте теоретические материалы, практикуйтесь на задачках, а за другими полезными формулами и самыми хитрыми заданиями приходите на онлайн-курсы математики для детей в Skysmart.
Основное тригонометрическое тождество
9 класс, 10 класс, ЕГЭ/ОГЭ
Связь между sin и cos одного угла
Вы уже наверняка знаете, что тождественный — это равный.
Основные тригонометрические тождества — это равенства, которые устанавливают связь между синусом, косинусом, тангенсом и котангенсом одного угла. Это значит, что любую из этих функций можно найти, если известна другая функция.
Ключ к сердцу тригонометрии — основное тригонометрическое тождество. Запомните и полюбите его, чтобы отношения с тригонометрией сложились самым наилучшим образом:
sin 2 α + cos 2 α = 1
Из основного тождества вытекают равенства тангенса и котангенса, поэтому оно — ключевое.
Равенство tg 2 α + 1 = 1/cos 2 α и равенство 1 + сtg 2 α + 1 = 1/sin 2 α выводят из основного тождества, разделив обе части на sin 2 α и cos 2 α.
В результате деления получаем:
Поэтому основному тригонометрическому тождеству уделяется максимум внимания. Но какая же «метрия» может обойтись без доказательств. Видите тождество — доказывайте, не раздумывая.
sin 2 α + cos 2 α = 1
Сумма квадратов синуса и косинуса одного угла тождественно равна единице.
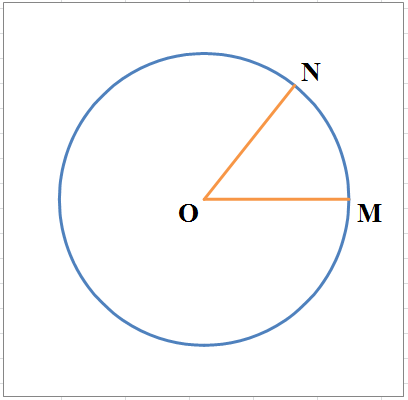
Чтобы доказать тождество, обратимся к теме единичной окружности.
Единичная окружность — это окружность с центром в начале прямоугольной декартовой системы координат. Радиус единичной окружности равен единице.
Докажем тождество sin 2 α + cos 2 α = 1
Образовался прямоугольный треугольник OA1B.
Основное тригонометрическое тождество связывает синус угла и косинус угла. Зная одно, вы легко можете найти другое. Нужно лишь извлечь квадратный корень по формулам:
Как видите, перед корнем может стоять и минус, и плюс. Основное тригонометрическое тождество не дает понять, положительным или отрицательным был исходный синус/косинус угла.
Как правило, в задачках с подобными формулами уже есть условия, которые помогают определиться со знаком. Обычно такое условие — указание на координатную четверть. Таким образом без труда можно определить, какой знак нам требуется.
Тангенс и котангенс через синус и косинус
Из всего этого множества красивых, но не сильно понятных слов, можно сделать вывод о зависимости одного от другого. Такая связь помогает отдельно преобразовывать нужные величины.
Исходя из определений:
Это позволяет сделать вывод, что тригонометрические тождества

задаются sin и cos углов.
Отсюда следует, что тангенс угла — это отношение синуса угла к косинусу. А котангенс угла — это отношение косинуса к синусу.
Отдельно стоит обратить внимание на то, что тригонометрические тождества

верны для всех углов α, значения которых вписываются в диапазон.
применимо для любого угла α, не равного π * z, где z — это любое целое число.
Курсы подготовки к ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.
Связь между тангенсом и котангенсом
Уж насколько очевидной кажется связь между ранее рассмотренными тождествами, настолько еще более наглядна связь между тангенсом и котангенсом одного угла.
Такое тождество применимо и справедливо при любых углах α, значение которых не равняются π/2 * z, где z — это любое целое число. В противном случае, функции не будут определены.
Как и любое другое, данное тригонометрическое тождество подлежит доказательству. Доказывать его очень просто.
tg α * ctg α = 1.
Получается, что тангенс и котангенс одного угла, при котором они имеют смысл — это взаимно обратные числа.
Если числа a и b взаимно обратные — это значит, что число a — это число, обратное числу b, а число b — это число, обратное числу a. Кроме того, это значит, что числу a обратно число b, а числу b обратно число a. Короче, и так, и эдак.
Тангенс и косинус, котангенс и синус
Все тождества выше позволяют сделать вывод, что тангенс угла связан с косинусом угла, а котангенс угла — с синусом.
Эта связь становится очевидна, если взглянуть на тождества:
Сумма квадрата тангенса угла и единицы равна числу, обратному квадрату косинуса этого угла.
Сумма единицы и квадрата котангенса угла равна числу, обратному квадрату синуса этого угла.
Вывести оба этих тождества можно из основного тригонометрического тождества:
sin 2 α + cos 2 α = 1.
Хорошо бы выучить все формулы и запомнить формулировки тождеств наизусть. Чтобы это сделать, сохраняйте себе табличку с основными формулами.
Основные тригонометрические тождества
sin 2 α + cos 2 α = 1
tg 2 α + 1 =
1 + ctg 2 α =
Чтобы тратить еще меньше времени на решение задач, сохраняйте таблицу значений тригонометрических функции углов, которые чаще всего встречаются в задачах.
Примеры решения задач
Разберем пару задачек, для решения которых нужно знать основные тождества. Рассмотрите внимательно предложенные решения и потренируйтесь самостоятельно.
Задачка 1. Найдите cos α, tg α, ctg α при условии, что sin α = 12/13.
Задачка 2. Найдите значение cos α,
если:
Подставляем значения sin α:
Как видите, задачи решаются достаточно просто, нужно лишь верно применять формулы основных тождеств.
Преобразования графиков тригонометрических функций
Общие принципы преобразования графиков функций изучались нами в главе 8, (см. §47, §48, §50 справочника для 8 класса). В этом параграфе мы рассмотрим особенности тригонометрических функций при использовании этих преобразований.
п.1. Растяжение и сжатие графиков тригонометрических функций по оси OX
Общие принципы растяжения и сжатия графиков по оси OX:
Эти принципы справедливы и для тригонометрических функций.
Тригонометрические функции являются периодическими: синус и косинус с периодом 2π, тангенс и котангенс – с периодом π. Получаем следствие общих принципов:
п.2. Растяжение и сжатие графиков тригонометрических функций по оси OY
Общие принципы растяжения и сжатия графиков по оси OY:
Общий принцип сжатия графиков:
Эти принципы справедливы и для тригонометрических функций.
Т.к. для графиков синуса и косинуса (синусоиды) характерна амплитуда колебаний, то также говорят, что:
п.3. Параллельный перенос графиков тригонометрических функций по оси OX
Общие принципы переноса по оси OX:
Эти принципы справедливы и для тригонометрических функций.
При этом параметр x называют начальной фазой колебаний.
При сравнении двух тригонометрических функций \(y_1=f(x)\) и \(y_2=f(x\pm a)\) говорят, что у второй функции сдвиг по фазе равен \(\pm a\).
п.4. Параллельный перенос графиков тригонометрических функций по оси OY
Общие принципы переноса по оси OY:
Эти принципы справедливы и для тригонометрических функций.
п.5. Общее уравнение синусоиды
График \(y(x)=Acos(cx+d)+B\) также называют синусоидой. Термин «косинусоида» употребляется относительно редко.
Поскольку график косинуса получается из графика синуса сдвигом по фазе на π/2 влево, вводить термин «косинусоида» излишне.
Построим график \(g(x)=3sin\left(2x+\frac\pi2\right)-1\)
По сравнению с \(f(x)=sinx\):
п.6. Общее уравнение тангенцоиды
График \(y(x)=Actg(cx+d)+B\) также называют тангенцоидой.
Построим график \(g(x)=\frac12 tg\left(\frac
По сравнению с \(f(x)=tgx\):
п.7. Примеры
Пример 2. Найдите наименьшие положительные периоды функций:
a) \(y=sin5x\)
Период синуса \(2\pi\) уменьшается в 5 раз. Получаем: \(T=\frac<2\pi><5>\)
б) \(y=cos\pi x\)
Период косинуса \(2\pi\) уменьшается в \(\pi\) раз. Получаем: \(T=\frac<2\pi><\pi>=2\)
в) \(y=tg\frac
Период тангенса \(\pi\) увеличивается в 4 раза. Получаем: \(T=4\pi\)
г) \(y=tg\left(2x+\frac<\pi><3>\right)\)
Период тангенса \(\pi\) уменьшается в 2 раза. Получаем: \(T=\frac\pi2\)
Пример 4. Определите графически, сколько корней имеет уравнение на отрезке: a) \(sinx=sin2x\) при \(0\leq x\leq 3\pi\)
Ответ: 7 корней
б) \(cos\frac
Ответ: 7 корней
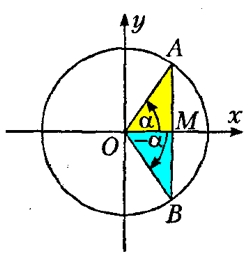
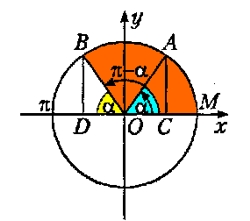
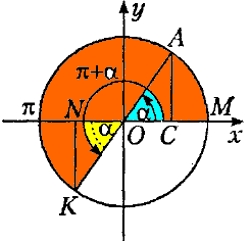
Формулы приведения углов
Формулы приведения позволяют выразить тригонометрические функции углов вида: π/2+α, π+α, 3π/2+α, 2π+α через тригонометрические функции угла α.
Зачем нужны формулы приведения?
Например, cos(530°) через формулы приведения можно преобразовать следующим образом:
На чем основан принцип формул приведения?
Формулы приведения для синуса
Формулы приведения для косинуса
Формулы приведения для тангенса
Формулы приведения для котангенса
Запомнить все формулы приведения достаточно непросто, ибо в них не прослеживается какой-либо явной закономерности.
Однако, это можно сделать, если понять принцип по которому в приведенной формуле происходит или не происходит смена функции на кофункцию и смена или не смена знака функции.
Когда надо менять название функции в формуле приведения?
Смена или не смена функции в формуле приведения зависит от того, к какому диаметру тригонометрического круга прилежит угол α в формуле приведения.
Когда надо менять знак функции в формуле приведения?
Для ответа на этот вопрос надо знать знаки функций синуса, косинуса, тангенса и котангенса в каждом квадранте тригонометрического круга.
Знак функции в формуле приведения ставится по квадранту исходного угла, при этом считаем, что сам угол α является острым.
Например, для угла π-α получается, что угол находится во II квадранте, т.к., π-α будет лежать в пределах от 90° до 180° (см. рисунок выше). Во втором квадранте синус положителен, поэтому, в формуле приведения надо будет ставить знак, идентичный знаку исходной функции, т. е., «плюс». Поскольку угол π-α прилежит к горизонтальному диаметру, то сама функция не меняется. Получается, что sin(π-α) = sin(α).
Десятиминутный ролик на ЮТуб, посмотрев который, вы навсегда запомните, как легко и просто приводить углы в тригонометрических функциях:
Пример решения уравнения с помощью формул приведения:
Если вам понравился сайт, будем благодарны за его популяризацию 🙂 Расскажите о нас друзьям на форуме, в блоге, сообществе. Это наша кнопочка:
Код кнопки: 
Политика конфиденциальности Об авторе
Как из косинуса перевести в синус – (sin cos)
Как выразить синус через косинус 🚩 как перевести синус косинус 🚩 Математика
Тригонометрия — один из любимых разделов алгебры для всех, кто любит справляться с уравнениями, выполнять кропотливые преобразования, обладает внимательностью и терпением. Знание основных теорем и формул позволяет находить не только правильное, но и наиболее красивое решение многих задач, в том числе физических или геометрических. Даже просто выразив синус через косинус, вы можете натолкнуться на решение.
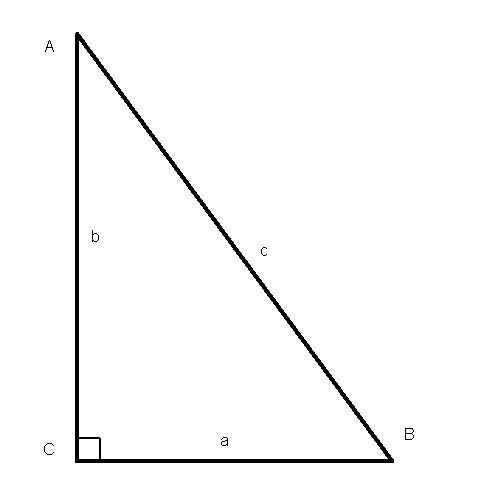
Воспользуйтесь знаниями планиметрии, чтобы выразить синус через косинус. Согласно определению, синусом угла в прямоугольном треугольнике называется отношение длины противолежащего катета к гипотенузе, а косинусом – прилежащего катета к гипотенузе. Даже знание простой теоремы Пифагора позволит вам в некоторых случаях быстро найти искомое преобразование.
Выразите синус через косинус, воспользовавшись простейшим тригонометрическим тождеством, согласно которому сумма квадратов этих величин дает единицу. Обратите внимание, что корректно выполнить задание вы сможете, только если знаете, в какой четверти находится искомый угол, в противном случае вы получите два возможных результата – с положительным и отрицательным знаком.
Запомните формулы приведения, также позволяющие осуществить необходимую операцию. Согласно им, если к числу π/2 прибавить (или отнять от него) угол а, то образуется косинус этого угла. Те же операции с числом 3π/2 дают косинус, взятый с отрицательным знаком. Соответственно, в случае, если вы работаете с косинусом, то синус вам позволит получить прибавление или вычитание из 3π/2, а его отрицательное значение – из π/2.
Воспользуйтесь формулами для нахождения синуса или косинуса двойного угла, чтобы выразить синус через косинус. Синус двойного угла есть удвоенное произведение синуса и косинуса этого угла, а косинус удвоенного угла – разность между квадратами косинуса и синуса.
Обратите внимание и на возможность обращения к формулам суммы и разности синусов и косинусов двух углов. Если вы выполняете операции с углами а и с, то синус их суммы (разности) – это сумма (разность) произведения синусов этих углов и их косинусов, а косинус суммы (разности) есть разность (сумма) произведения косинусов и синусов углов, соответственно.
Не получили ответ на свой вопрос?
Спросите нашего эксперта:
Как из косинуса сделать синус и наоборот?
Потому что вычитая π/2 радиан вы меняете местами катеты прямоугольного треугольника, а гипотенуза его остаётся прежней длины.
Косинус и синус есть длины проекции на координатные оси, которые получаются, если провернуть гипотенузу на некоторый угол. Поэтому, если нужно получить cos(pi/2) из синуса, то достаточно взять то же значение: sin(0). Если ты прокрутишь гипотенузу выражения cos(pi/6) на 180 градусов, то есть cos(pi/6 + pi), то ты получишь то же значение, только в другой части оси Ox. С синусом та же история, так как синус можно рассматривать как повёрнутый косинус. Чтобы получить что-то из cos(pi/3), нужно провернуть гипотенузу только на половину от 180: cos(pi/3 + pi/2). В итоге ты получишь результат, который можно трактовать как sin(pi/3). Просто меняешь проекцию. Есть мнемоническое правило: если в тригонометрическом круге угол поворота заставляет тебя точно кивнуть или точно помахать головой влево-вправо, то здесь можно сделать преобразование: видя аргумент, кратный pi, то есть либо 180, либо 360 градусов, его можно просто отбросить, учитывая знак, не изменяя саму функцию. Когда ты хочешь провернуть гипотенузу на половину от 180, то есть pi/2 либо 3pi/2, то это значит, что можно изменить функцию, отбросив этот поворот, учитывая получившийся знак. Если такое вольное объяснение непонятно — гугли «Правила приведения тригонометрических функций»
Без — никак. Конечно, есть углы, для которых синус равен косинусу. Но их немного.
Обычный фазовый сдвиг на 90 (pi/2) градусов (в любую сторону) легко решит твою задачу безо всяких преобразований… Пример: |Cos(60)| = |Sin(150)| = |Sin(-30)| = |Cos(240)| и т. д. и т. п….
cos(pi/2-x)=sin(x) если это нужно.
Косинус опережает синус на 90° Значит, cosx-90°=sinx Синус отстает от косинуса. Значит, sinx+90°=cos
Как выразить синус через косинус
Инструкция
5. Обратите внимание и на вероятность обращения к формулам суммы и разности синус ов и косинус ов 2-х углов. Если вы исполняете операции с углами а и с, то синус их суммы (разности) – это сумма (разность) произведения синус ов этих углов и их косинус ов, а косинус суммы (разности) есть разность (сумма) произведения косинус ов и синус ов углов, соответственно.
Инструкция
2. Если треугольник прямоугольный, то для нахождения косинус а угла довольно знать длины каждого 2-х всяких сторон (косинус прямого угла равен 0).Пускай имеется прямоугольный треугольник со сторонами а, b, с, где с – гипотенуза.Разглядим все варианты:Пример 2.Обнаружить соs?, если знамениты длины сторон а и b (катеты треугольника)Воспользуемся добавочно теоремой Пифагора:c?=b?+а?,с=v(b?+а?)соs?=(b?+c?-а? )/(2*b*c)=(b?+b?+а?-а?)/(2*b*v(b?+а?))=(2*b?)/(2*b*v(b?+а?))=b/v(b?+а?)Дабы проверить правильность полученной формулы, подставим в нее значения из примера 1, т.е.а=3,b=4.Проделав элементарные вычисления, получаем:соs?=0,8.
3. Подобно находится косинус в прямоугольном треугольнике в остальных случаях:Пример 3.Вестимы а и с (гипотенуза и противолежащий катет), обнаружить соs?b?=с?-а?,b=v(c?-а?)соs?=(b?+c?-а? )/(2*b*c)=(с?-а?+с?-а?)/(2*с*v(с?-а?))=(2*с?-2*а?)/(2*с*v(с?-а?))=v(с?-а?)/с.Подставляя значения а=3 и с=5 из первого примера, получаем:соs?=0,8.
Для того дабы получить формулу, объединяющую синус и косинус угла, нужно дать либо припомнить некоторые определения. Так, синус угла – это отношение (частное от деления) противолежащего катета прямоугольного треугольника к гипотенузе. Косинус угла – это отношение прилежащего катета к гипотенузе.
Инструкция
1. Нарисуем прямоугольный треугольник АВС, где угол АВС – прямой (рис.1). Разглядим соотношение синус а и косинус а угла САВ. По данному выше определениюsin CAB=BC/AC, cos CAB=AB/AC.
2. Припоминаем теорему Пифагора – АВ^2 + BC^2 = AC^2, где ^2 – операция возведения в квадрат.Поделим левую и правую части уравнения на квадрат гипотенузы AC. Тогда предыдущее равенство будет выглядеть так:АВ^2/AC^2 + BC^2/AC^2 = 1.
3. Для комфорта перепишем равенство, полученное на шаге 2, дальнейшим образом:(AB/AC)^2 + (BC/AC)^2 = 1.Согласно определениям, данным на шаге 1, получаем:cos^2(CAB) + sin^2(CAB) = 1, т.е.cos(CAB)=SQRT(1-sin^2(CAB)), где SQRT – операция взятия квадратного корня.
Полезный совет
Величина синуса и косинуса всякого угла не может быть огромнее 1.
Синус и косинус – это прямые тригонометрические функции, для которых существует несколько определений – через окружность в декартовой системе координат, через решения дифференциального уравнения, через острые углы в прямоугольном треугольнике. Всякое из таких определений дозволяет вывести связанность между этими двумя функциями. Ниже приведен самый, вероятно, примитивный метод выразить косинус через синус – через их определения для острых углов прямоугольного треугольника.
Инструкция
1. Выразите синус острого угла прямоугольного треугольника через длины сторон этой фигуры. Согласно определению, синус угла (?) должен быть равен отношению длины стороны (a), лежащей наоборот него – катета – к длине стороны (c), противолежащей прямому углу – гипотенузы: sin(?) = a/c.
2. Обнаружьте аналогичную формулу для косинус а того же угла. По определению эта величина должна выражаться отношением длины стороны (b), примыкающей к этому углу (второго катета), к длине стороны (c), лежащей наоборот прямого угла: cos(а) = a/c.
3. Перепишите равенство, вытекающее из теоремы Пифагора, таким образом, дабы в нем были задействованы соотношения между катетами и гипотенузой, выведенные на 2-х предыдущих шагах. Для этого вначале поделите обе части начального уравнения этой теоремы (a? + b? = c?) на квадрат гипотенузы (a?/c? + b?/c? = 1), а после этого полученное равенство перепишите в таком виде: (a/c)? + (b/c)? = 1.
5. Если помимо всеобщего решения надобно получить численный итог, воспользуйтесь, скажем, калькулятором, встроенным в операционную систему Windows. Ссылку на его запуск обнаружьте в подразделе «Типовые» раздела «Все программы» основного меню ОС. Эта ссылка сформулирована немногословно – «Калькулятор». Дабы иметь вероятность вычислять с поддержкой этой программы тригонометрические функции включите ее «инженерный» интерфейс – нажмите комбинацию клавиш Alt + 2.
6. Введите данное в условиях значение синуса угла и кликните по кнопке интерфейса с обозначением x? – так вы построите начальное значение в квадрат. После этого наберите на клавиатуре *-1, нажмите Enter, введите +1 и нажмите Enter еще раз – таким методом вы вычтите из единицы квадрат синуса. Щелкните по клавише со значком радикала, дабы извлечь квадратный корень и получить окончательный итог.
Одной из фундаментальных основ точных наук является представление о тригонометрических функциях. Они определяют примитивные отношения между сторонами прямоугольного треугольника. К семейству данных функций относится синус. Обнаружить его, зная угол, дозволено огромным числом методов, включающих экспериментальные, вычислительные способы, а также применение справочной информации.
Вам понадобится
Инструкция
1. Используйте калькулятор с функцией вычисления синуса для приобретения необходимых значений на основании познания угла. Сходственный функционал сегодня имеют даже самые примитивные устройства. При этом вычисления производятся с дюже высокой степенью точности (как водится, до восьми и больше знаков позже запятой).
2. Примените программное обеспечение, представляющее собой среду для работы с электронными таблицами, запущенное на персональном компьютере. Примерами сходственных приложений являются Microsoft Office Excel и OpenOffice.org Calc. Введите в всякую ячейку формулу, состоящую из вызова функции вычисления синуса с необходимым доводом. Нажмите Enter. В ячейке отобразится желанная величина. Превосходством электронных таблиц является вероятность стремительного расчета значений функций для большого комплекта доводов.
3. Узнайте приближенное значение синуса угла из таблиц Брадиса, если они имеются в наличии. Их недостатком является точность значений, ограниченная четырьмя знаками позже запятой.
4. Обнаружьте приближенное значение синуса угла, совершив геометрические построения. На листе бумаги вычертите отрезок. При помощи транспортира отложите от него угол, синус которого нужно обнаружить. Начертите еще один отрезок, пересекающий 1-й в некоторой точке. Перпендикулярно первому же отрезку проведите прямую линию, пересекающую два теснее существующих отрезка. Получится прямоугольный треугольник. Измерьте длину его гипотенузы и катета, противолежащего углу, построенному при помощи транспортира. Поделите второе значение на первое. Это и будет желанная величина.
5. Рассчитайте синус угла, применяя разложение в ряд Тейлора. Если значение угла представлено в градусах, переведите его в радианы. Используйте формулу вида: sin(х) = х – (х^3)/3! + (х^5)/5! – (х^7)/7! + (х^9)/9! – … Для возрастания скорости расчетов записывайте нынешнее значение числителя и знаменателя последнего члена ряда, производя вычисление дальнейшего значения на основе предыдущего. Увеличивайте длину ряда для приобретения больше точной величины.
Видео по теме
Постижение треугольников ведется математиками на протяжении нескольких тысячелетий. Наука о треугольниках – тригонометрия – использует особые величины: синус и косинус.
Прямоугольный треугольник
Изначально синус и косинус появились из-за необходимости рассчитывать величины в прямоугольных треугольниках. Было подмечено, что если значение градусной меры углов в прямоугольном треугольнике не менять, то соотношение сторон, насколько бы эти стороны ни изменялись в длине, остается неизменно идентичным.Именно так и были введены представления синуса и косинуса. Синус острого угла в прямоугольном треугольнике – это отношение противолежащего катета к гипотенузе, а косинус – прилежащего к гипотенузе.
Теоремы косинусов и синусов
Но косинусы и синусы могут использоваться не только в прямоугольных треугольниках. Дабы обнаружить значение тупого либо острого угла, стороны всякого треугольника, довольно применить теорему косинусов и синусов.Теорема косинусов достаточно примитивна: «Квадрат стороны треугольника равен сумме квадратов 2-х других сторон за вычетом удвоенного произведения этих сторон на косинус угла между ними». Существует две трактовки теоремы синусов: малая и расширенная. Согласно малой: «В треугольнике углы пропорциональны противолежащим сторонам». Данную теорему зачастую расширяют за счет свойства описанной около треугольника окружности: «В треугольнике углы пропорциональны противолежащим сторонам, а их отношение равно диаметру описанной окружности».
Производные
Производная – математический инструмент, показывающий, как стремительно меняется функция касательно метаморфозы ее довода. Производные применяются в алгебре, геометрии, экономике и физике, ряде технических дисциплин. При решении задач требуется знать табличные значения производных тригонометрических функций: синуса и косинуса. Производной синуса является косинус, а косинуса – синус, но со знаком «минус».
Применение в математике
Особенно зачастую синусы и косинусы применяются при решении прямоугольных треугольников и задач, связанных с ними. Удобство синусов и косинусов обнаружило свое отражение и в технике. Углы и стороны было примитивно оценивать по теоремам косинусов и синусов, разбивая трудные фигуры и объекты на «примитивные» треугольники. Инженеры и архитекторы, зачастую имеющие дело с расчетами соотношения сторон и градусных мер, тратили много времени и усилий для вычисления косинусов и синусов не табличных углов. Тогда «на подмогу» пришли таблицы Брадиса, содержащие тысячи значений синусов, косинусов, тангенсов и котангенсов различных углов. В советское время некоторые преподаватели принуждали своих подопечных учить страницы таблиц Брадиса назубок.
Формулы тригонометрии
В этой статье мы изучим все тригонометрические формулы, которые могут понадобится на ЕГЭ.
От основного тригонометрического тождества, до формул тройного угла.
Мы решим вместе 22 примера, чтобы «набить руку» и уметь решать любые задачи.
Формулы тригонометрии — коротко о главном
Основные формулы:
| Название формулы | Формула |
|---|---|
| Основное тригонометрическое тождество (ночью разбудят — должен вспомнить!) | \( \displaystyle si< |
| Выражение тангенса через синус и косинус (по сути альтернативное определение тангенса) | \( \displaystyle tg\ \alpha =\frac |
| Выражение котангенса через синус и косинус или через тангенс (по сути альтернативное определение котангенса) | \( \displaystyle ctg\ \alpha =\frac |
| Синус суммы и разности: | \( \displaystyle \sin \left( \alpha \pm \beta \right)=sin\alpha \cdot cos\beta \pm cos\alpha \cdot sin\beta \) |
| Косинус суммы и разности: | \( \displaystyle \cos \left( \alpha \pm \beta \right)=cos\alpha \cdot cos\beta \mp sin\alpha \cdot sin\beta \) |
| Тангенс суммы и разности: | \( \displaystyle tg\left( \alpha \pm \beta \right)=\frac |
Формулы понижения степени:
Данная группа формул позволяет перейти от любого тригонометрического выражения к рациональному.
Формулы преобразования функций:
Данная группа формул позволяет преобразовать произведение в сумму и сумму в произведение.
Формулы преобразования произведений функций:
Таблица значений тригонометрических функций:
Тригонометрические функции
Как ты уже понял, тригонометрические выражения – это выражения, в котором переменная содержится под знаком тригонометрических функций.
Стоп! Вот прямо здесь мы и остановимся! Я задам тебе вопрос: какие тригонометрические функции ты знаешь?
Верно! Их всего четыре!
Хотя, положа руку на сердце, я скажу тебе, что знание последней не так уж и обязательно (хотя желательно!), поскольку она легко выражается через тангенс.
Да и сам тангенс, по сути – тоже лишь тригонометрическое выражение, зависящее от синуса и косинуса.
Таким образом, у нас есть две основные тригонометрические функции – синус и косинус и две «второстепенные» – тангенс и котангенс.
Я не буду сейчас определять, что такое синус и косинус, ты и так это уже знаешь из предыдущих разделов. Я лишь скажу пару слов про важность этих понятий.
Итак, пара слов: первые зачатки тригонометрии возникли более 3 тысяч лет назад. Я думаю, что тебе очевидно, что тогда люди не занимались «формулами ради формул».
Так что тригонометрические функции имеют полезные практические свойства. Я не буду их перечислять. Если тебе интересно, ты всегда можешь найти море информации в интернете.
Если все, что я сказал выше, звучало для тебя древним эльфийским языком, то посмотри статью о тригонометрической окружности.
А сейчас я приведу тебе некоторые основные соотношения между тригонометрическими величинами, которые оказываются полезными при решении задач.
Таблица значений тригонометрических функций
Тебе нужно помнить таблицу значений тригонометрических функций для углов хотя бы первой четверти! Я сейчас нарисую здесь эту таблицу, а потом объясню тебе, как сделать ее запоминание проще.
Или ее расширенный вариант для всех «основных углов»:
Я ни в коей мере не настаиваю (и даже не надеюсь), что ты выучишь вторую таблицу. Сказать по правде, я и сам ее не знаю.
Но первую таблицу знать совершенно необходимо.
Не всегда на экзамене у тебя будет время, чтобы вывести самостоятельно, скажем, синус \( \displaystyle 60\) градусов.
Для того, чтобы запомнить первую таблицу можно поступить так:
Запомнить всего 5 значений для, скажем, синуса. Затем тебе не составит труда заметить, что для косинуса все значения идут «наоборот»:
Тангенс можно получить, разделив синус угла на косинус. Как же всегда вывести большую таблицу, зная малую, я тебе непременно расскажу чуть позднее.
Формулы тригонометрии (основа)
| Название формулы | Формула |
|---|---|
| Основное тригонометрическое тождество (ночью разбудят — должен вспомнить!) | \( \displaystyle si< |
| Выражение тангенса через синус и косинус (по сути альтернативное определение тангенса) | \( \displaystyle tg\ \alpha =\frac |
| Выражение котангенса через синус и косинус или через тангенс (по сути альтернативное определение котангенса) | \( \displaystyle ctg\ \alpha =\frac |
| Первое следствие формулы 1: | \( \displaystyle t< |
| Второе следствие формулы 1: | \( \displaystyle ct< |
| Третье следствие формулы 1: | \( \displaystyle sin\ \alpha =\pm \sqrt<1-co< |
| Четвертое следствие формулы 1: | \( \displaystyle cos\ \alpha =\pm \sqrt<1-si< |
Уже получилось 7 формул! К сожалению, это еще далеко не предел. Совсем не предел.
Тем не менее последние 4 формулы есть ни что иное, как простое следствие первой. В самом деле, ты заметил, почему это так?
Формула 4 получается делением обеих частей формулы 1 на \( \displaystyle co<^<2>>\alpha \) и применением формулы 2.
Формула 5 получается аналогично: разделим обе части формулы 1 на \( \displaystyle si<
Формулы 1 – 5 мы трактуем вполне однозначно. Чего нельзя сказать про формулы 6 и 7. В чем «фишка» формул 6 и 7?
Их особенность заключается в знаке \( \displaystyle \pm \), который стоит перед корнем.
Как это понимать? А понимать надо так: в некоторых случаях мы ставим плюс, а в некоторых – минус.
Теперь у тебя должен возникнуть вопрос: в каких-таких «некоторых случаях»? Туманность этой формулировки снимается следующим правилом:
Если в формуле
\( \displaystyle sin\ \alpha =\pm \sqrt<1-co<^<2>>\alpha >\)
угол \( \displaystyle \alpha \) таков, что \( \displaystyle \text\ \text< >\!\!\alpha\!\!\text < >
Они подскажут тебе, какой нужно выбирать знак для той или иной функции, так что ты не допустишь досадной ошибки.
К тому же это избавит тебя от мучительных размышлений по поводу того «а зачем в этом примере нужен этот угол?!».
4 примера на тренировку
Решения:
Теперь дело за малым: разобраться со знаком. Что нам для этого нужно? Знать, в какой четверти находится наш угол.
По условию задачи: \( \displaystyle \alpha \in \left( \frac<3\pi ><2>;2\pi \right)\). Смотри на картинку. Какая это четверть? Четвертая.
Каков знак косинуса в четвертой четверти? На картинке стоит знак «плюс», значит косинус в четвертой четверти положительный.
Тогда нам остается выбрать знак «плюс» перед \( \displaystyle \frac<1><3>\). \( \displaystyle \text
Ответ: \( \displaystyle 1\).
Ну вот видишь, ничего сложного. Абсолютно ничего. Нужно лишь запомнить знаки синуса, косинуса и тангенса (котангенса) по четвертям. Ну а как это делать автоматически описано в статье, посвященной тригонометрической окружности.
Давай разберем оставшиеся примеры.
2. Так как \( \displaystyle sin\ \alpha =\pm \sqrt<1-co<^<2>>\alpha >\), то все, что нам нужно – это подставить \( \displaystyle cos\alpha =\frac<2\sqrt<6>><5>\) в нашу формулу. Что мы с тобой и сделаем:
Опять нужно определиться со знаком. Смотрим на рисунок. Четверть – снова четвертая. Знак синуса четвертой четверти – отрицательный. Ставим знак «минус». \( \displaystyle sin\alpha =-\frac<1><5>\), тогда \( \displaystyle 5sin\alpha =-5\cdot \frac<1><5>=-1\).
3. Ничего нового. Скорее для закрепления. Снова подставляем в формулу \( \displaystyle cos\ \alpha =\pm \sqrt<1-si<
Смотрим на знак косинуса при \( \displaystyle \alpha \in \left( \frac<\pi ><2>;\pi \right)\). Какая это четверть? Вторая. Косинус второй четверти отрицательный. Тогда выбираем знак «минус».
4. Здесь перед нами стоит задачка чуть сложнее. Однако, не стоит огорчаться. Давай вспомним, что такое тангенс. Это ведь отношение синуса к косинусу. Синус нам уже дан.
Так как \( \displaystyle \alpha \in \left( \pi ;\frac<3\pi > <2>\right)\) (это угол в третьей четверти, а косинус в третьей четверти имеет знак «минус»), то \( \displaystyle cos\alpha =-\frac<1><\sqrt<26>>\).
Теперь все, что нам осталось, это воспользоваться определением тангенса:
Ответ: \( \displaystyle 5\).
Уф, выдохнули! Ну вот мы с тобой решили некоторые (довольно типичные и распространенные) примеры. Ты спросишь: «И что, это все?». Я отвечу, что, увы нет. Это далеко не все.
Далее нам потребуются более сложные формулы тригонометрии.
Формулы тригонометрии (более сложные)
| Название формулы | Формула |
|---|---|
| Синус суммы и разности: | \( \displaystyle \sin \left( \alpha \pm \beta \right)=sin\alpha \cdot cos\beta \pm cos\alpha \cdot sin\beta \) |
| Косинус суммы и разности: | \( \displaystyle \cos \left( \alpha \pm \beta \right)=cos\alpha \cdot cos\beta \mp sin\alpha \cdot sin\beta \) |
| Тангенс суммы и разности: | \( \displaystyle tg\left( \alpha \pm \beta \right)=\frac |
| Синус двойного угла (следствие формулы 1) | \( \displaystyle sin2a=2sina\cdot cosa\) |
| Косинус двойного угла (следствие формулы 2) | \( \displaystyle cos2a=co< \( \displaystyle cos2a=2co< |
| Тангенс двойного угла: | \( \displaystyle tg2a=\frac<2tga><1-t< |
Как распознать, что тебе требуются именно эти, а не какие-нибудь другие формулы?
Очень просто: если ты видишь косинус, синус, тангенс от суммы двух углов или двойных углов, то это должно служить тебе индикатором – мне нужно применить одну из формул для суммы/разности или для двойного угла.
Звучит несколько путано? Давай посмотрим на примеры. Заодно я дам еще ряд важных комментариев.
9 примеров на тренировку
Список этих заданий можно продолжать бесконечно… Но я выбрал здесь: а) не самые сложные формулы; б) не самые «страшные» углы.
Страшные углы я припас нам напоследок 🙂
Решения:
Кстати, здесь тебе понадобится знание также тех формул, которые я привел в самом начале. Поехали!
1. \( \displaystyle \frac<12sin11<>^\circ cos11<>^\circ >
Ни ты, ни я не знаем, чему в точности равен синус или косинус \( \displaystyle 11\) градусов, и чему равен синус \( \displaystyle 22\) градусов.
Но что мы должны заметить?
Верно! \( \displaystyle 22<>^\circ =2\cdot 11<>^\circ \). Значит, снизу записан синус двойного угла! Тогда применим формулу синуса двойного угла:
\( \displaystyle sin22<>^\circ =2sin11<>^\circ \cdot cos11<>^\circ \)
Подставим это значение в знаменатель нашей дроби и сократим!
\( \displaystyle \frac<12sin11<>^\circ \cdot cos11<>^\circ >
Ответ: \( \displaystyle 6\).
Ну вот, ничего страшного не случилось? Пример решился в одну строчку с применением одной единственной формулы. Другое дело, иногда не совсем очевидно, какую из формул применять.
Тут тебе нужен опыт. Нужно, как говорится, «набить руку» на таких примерах.
Опять-таки, сразу можно заметить, что \( \displaystyle 34<>^\circ =2\cdot 17<>^\circ \). \( \displaystyle 34\) градуса стоит в косинусе. Это говорит о том, что в примере спрятан косинус двойного угла. Вспомним его определение:
Что же у нас есть в числителе? А там все наоборот: синус в квадрате вычитается из косинуса в квадрате. Тогда в числителе у нас написана формула чего?
Открыть ответы…
Чтобы открыть все задачи учебника, закрытые голубыми баннерами (как этот), зарегистрируйтесь один раз:
3. \( \displaystyle 36\sqrt<6>ctg\frac<\pi ><6>\sin\frac<\pi ><4>\)
Здесь нет ничего сложного, абсолютно ничего! Но есть одно «но!».
Это «но» заключается в том, что тебе нужно помнить таблицу значений тригонометрических функций для углов хотя бы первой четверти! (Как ее запомнить я рассказал ранее, а сейчас просто приведу ее еще раз).
Или ее расширенный вариант для всех «основных углов»:
И посмотрим в таблицу:
\( \displaystyle ctg\frac<\pi ><6>=\sqrt<3>\), \( \displaystyle sin\frac<\pi ><4>=\frac<\sqrt<2>><2>\). Подставим эти значения в нашу формулу:
Ответ: \( \displaystyle 108\)
Вот видишь, знание первой таблицы совершенно необходимо! Без нее – вообще нет никакой тригонометрии. Так что, пожалуйста, будь добр, выучи.
Это не потребует от тебя значительных усилий и избавит от массы глупых ошибок в будущем. Еще раз специально скажу: большую таблицу учить не надо.
4. По условию \(cosa=-0,4\), нам же надо найти \(-47cos2a\).
Что тогда надо сделать?
Верно, наша цель – выразить косинус двойного угла через угол «одинарный». Есть ли такая формула? Конечно, есть! Вот она:
Открыть ответы…
Чтобы открыть все задачи учебника, закрытые голубыми баннерами (как этот), зарегистрируйтесь один раз:
5. \( \displaystyle \frac<10sin6a><3cos3a>\) – это то, что надо вычислить, а \( \displaystyle sin3a=0,6\) – это то, что есть.
Ну что же, надо отталкиваться от того, что есть. Вроде бы этого должно быть достаточно. Здесь все опять несложно!
Нужно лишь заметить, что \( \displaystyle sin6\alpha =2sin3\alpha \cdot cos3\alpha \). Давай это и подставим в числитель исходной дроби. Что же мы имеем?
Открыть ответы…
Чтобы открыть все задачи учебника, закрытые голубыми баннерами (как этот), зарегистрируйтесь один раз:
6. \( \displaystyle 26\text
На самом деле здесь можно поступать двояко. Но о втором способе я скажу тебе чуть позже. А пока давай подумаем, что нужно найти.
А найти нужно по сути косинус от суммы двух углов. Причем один из них известен. Давай не будем долго думать и разложим косинус суммы на произведение:
Вспомни единичную окружность (ну или на худой конец посмотри в расширенную таблицу).
\frac<3\pi ><2>=270<>^\circ \) равен нулю!
Открыть ответы…
Чтобы открыть все задачи учебника, закрытые голубыми баннерами (как этот), зарегистрируйтесь один раз:
7. Нужно найти: \( \displaystyle t<^<2>>a=6\).
Тут все можно сделать только зная, что такое тангенс и основное тригонометрическое тождество. По порядку:
Тогда решить задачу можно вот как: найти по отдельности значения синуса в квадрате и косинуса в квадрате, а затем при помощи полученных значений найти тангенс. Так мы с тобой и сделаем:
Вначале найдем синус в квадрате.
Открыть ответы…
Чтобы открыть все задачи учебника, закрытые голубыми баннерами (как этот), зарегистрируйтесь один раз:
8. Надо найти \( \displaystyle \frac<10cosa+4sina+15><2sina+5cosa+3>\), зная, что \( \displaystyle tga=-2,5\).
На какую мысль тебя это должно было натолкнуть?
А на ту, что если нам дан тангенс, то и наше выражение нужно привести к такому виду, чтобы оно зависело от тангенсов, которые мы потом в него и подставим. Напомню тебе, что
У меня же в выражении есть просто косинусы и синусы. Что нам нужно сделать?
Давай возьмем и «насильно» разделим числитель и знаменатель дроби на \( \displaystyle cos\alpha \). Это поможет мне «выделить» тангенс в чистом виде:
Открыть ответы…
Мы постоянно улучшаем этот учебник и вы можете нам в этом помочь.
Оформите доступ и пользуйтесь учебником ЮКлэва без ограничений (100+ статей по всем темам ОГЭ и ЕГЭ, 2000+ разобранных задач, 20+ вебинаров-практикумов)
9. Нужно найти \( \displaystyle 7\cos \left( \pi +\beta \right)-2\text
Давай опять проанализируем, что нам нужно вычислить: искомая формула состоит из разности косинуса от суммы двух углов и синуса от суммы двух углов.
Давай упрощать: раскроем каждую из сумм (опять-таки повторюсь, что далее я опишу способ, который позволит обходиться без раскрытия такого рода сумм):
Опять-таки, тебе должно быть известно, что \( \displaystyle cos\pi =-1,
Если тебе это неизвестно, то настоятельно рекомендую тебе повторить тему тригонометрическая окружность.
Тогда моя формула примет вид:
Открыть ответы…
Мы постоянно улучшаем этот учебник и вы можете нам в этом помочь.
Оформите доступ и пользуйтесь учебником ЮКлэва без ограничений (100+ статей по всем темам ОГЭ и ЕГЭ, 2000+ разобранных задач, 20+ вебинаров-практикумов)
Формулы приведения
Теперь мы знаем уже почти что все. Осталось совсем немного. Последнее, на что я хочу обратить внимание, это обещанный мною метод «легкого» перехода от большой таблицы значений углов к маленькой.
Этот переход обеспечивают так называемые формулы приведения. Еще раз поясню, зачем они используются: ты будешь их применять в том случае, когда тебе нужно найти синус, косинус или тангенс угла, большего чем \( \displaystyle 90\) градусов.
Например, найти синус угла \( \displaystyle 855\) градусов.
Здесь мы поступаем следующим образом. Во-первых, нам понадобятся следующие знания:
Алгоритм использования формул приведения
Шаг 1. Если мы вычисляем значение тригонометрической функции от отрицательного угла – делаем его положительным при помощи группы формул (2).
Шаг 2. Отбрасываем для синуса и косинуса его периоды: \( \displaystyle 2\pi k\) (по \( \displaystyle 360\) градусов), а для тангенса – «половинки» \( \displaystyle \pi k\) (\( \displaystyle 180\) градусов).
\( \displaystyle sin\ 855<>^\circ =sin\left( 2\cdot 360<>^\circ +135<>^\circ \right)=sin\ 135<>^\circ \)
\( \displaystyle tg\ 225<>^\circ =tg\left( 180<>^\circ +45<>^\circ \right)=tg\ 45<>^\circ \)
Шаг 3. Если оставшийся «уголок» меньше \( \displaystyle 90\) градусов, то задача решена: ищем его в «малой таблице»
Шаг 4. Иначе ищем, в какой четверти лежит наш угол \( \displaystyle \alpha \): это будет 2, 3 или 4 четверть. Смотрим, какой знак имеет искомая функция в четверти. Запомнили этот знак.
Шаг 5. Представляем угол \( \displaystyle \alpha \) в одной из следующих форм:
…так, чтобы оставшийся угол \( \displaystyle \beta \) был больше нуля и меньше \( \displaystyle 90\) градусов.
\( \displaystyle 135<>^\circ =90<>^\circ +45<>^\circ \)
\( \displaystyle 315<>^\circ =270<>^\circ+45<>^\circ \)
\( \displaystyle 240<>^\circ =180<>^\circ +60<>^\circ \)
В принципе не важно, в какой из двух альтернативных форм для каждой четверти ты представишь угол. На конечном результате это не скажется.
Шаг 6. Теперь смотрим, что у нас получилось:
Шаг 7. Ставим перед получившимся выражением знак из пункта 4.
3 примера на тренировку
Решения:
1. \( \displaystyle sin\ 2130<>^\circ \)
Действуем согласно нашему алгоритму. Выделяем целое число кругов для \( \displaystyle 2130<>^\circ \):
\( \displaystyle \frac<2130<>^\circ ><360<>^\circ >=5,91\ldots \)
\ 2130<>^\circ =sin\left( 5\cdot 360<>^\circ +330<>^\circ \right)=sin\ 330<>^\circ \)
Ну вот, лишнее мы отбросили. Теперь разбираемся со знаком.
\( \displaystyle 330<>^\circ \) лежит в 4 четверти. Синус четвертой четверти имеет знак «минус», его я и не должен забыть поставить в ответе. Далее, представляем \( \displaystyle 330<>^\circ \) согласно одной из двух формул пункта 5 правил приведения. Я выберу: \( \displaystyle 330<>^\circ =270<>^\circ +60<>^\circ \)
\( \displaystyle sin\ 330<>^\circ =sin\left( 270<>^\circ +60<>^\circ \right)\)
Теперь смотрим, что получилось: у нас случай с \( \displaystyle 270\) градусами, тогда отбрасываем \( \displaystyle 270<>^\circ \) и синус меняем на косинус. И ставим перед ним знак «минус»!
\( \displaystyle sin\left( 270<>^\circ +60<>^\circ \right)=-cos60<>^\circ \)
\( \displaystyle 60\) градусов – угол в первой четверти. Мы знаем (ты мне обещал выучить малую таблицу!) его значение:
\( \displaystyle cos\ 60<>^\circ =0,5\)
Тогда получим окончательный ответ:
Как из косинуса получить синус – (sin cos)
Как найти угол, если известен синус 🚩 найти угол по синусу онлайн 🚩 Математика
Синус и косинус — пара основных тригонометрических функций, которые косвенно выражают величину угла в градусах. Всего таких функций существует больше десятка и среди них есть те, что позволяют по значению, например, синуса восстановить величину угла в градусах. Для практической работы с ними можно использовать программный калькулятор или сетевые сервисы.
Используйте функцию арксинус для вычисления величины угла в градусах, если известно значение синуса этого угла. Если угол обозначить буквой α, в общем виде такое решение можно записать так: α = arcsin(sin(α)). Если у вас есть возможность пользоваться компьютером, для практических расчетов проще всего использовать встроенный калькулятор операционной системы. В последних двух версиях ОС Windows его можно запустить так: нажмите клавишу Win, наберите буквы «ка» и надавите Enter. В более ранних выпусках этой ОС ссылку «Калькулятор» ищите в подразделе «Стандартные» раздела «Все программы» главного меню системы.
После запуска приложения переключите его в режим, позволяющий работать с тригонометрическими функциями. Сделать это можно выбором строки «Инженерный» в разделе «Вид» меню калькулятора или нажатием клавиш Alt + 2.
Введите значение синуса. По умолчанию в интерфейсе калькулятора нет кнопки для вычисления арксинуса. Чтобы получить возможность использовать эту функцию, вам нужно инвертировать значения кнопок по умолчанию — кликните по клавише Inv в окне программы. В более ранних версиях эту кнопку заменяет чекбокс с таким же обозначением — поставьте в нем отметку.
Кликните по кнопке вычисления синуса — после инвертирования функций ее обозначение сменится на sin⁻¹. Калькулятор рассчитает угол и отобразит его величину.
Можно использовать в расчетах и различные онлайн-сервисы, которых более чем достаточно в интернете. Например, перейдите на страницу http://planetcalc.com/326/, прокрутите ее немного вниз и в поле Input введите значение синуса. Для запуска процедуры вычисления здесь предназначена оранжевая кнопка с надписью Calculate — кликните по ней. Результат вычислений вы найдете в первой строке таблицы под этой кнопкой. Кроме арксинуса в ней отображаются и величины арккосинуса, арктангенса и арккотангенса введенного значения.
Такие понятия как синус, косинус, тангенс вряд ли кому-то часто встречаются в повседневной жизни. Однако, если вы сели решать математические задачки с сыном-старшеклассником, неплохо было бы вспомнить, что же это за понятия, и как найти, например, косинус.
Для того чтобы получить формулу, связывающую синус и косинус угла, необходимо дать или вспомнить некоторые определения. Так, синус угла — это отношение (частное от деления) противолежащего катета прямоугольного треугольника к гипотенузе. Косинус угла — это отношение прилежащего катета к гипотенузе.
Нарисуем прямоугольный треугольник АВС, где угол АВС — прямой (рис.1). Рассмотрим соотношение синуса и косинуса угла САВ. По данному выше определению
sin CAB=BC/AC, cos CAB=AB/AC. Вспоминаем теорему Пифагора — АВ^2 + BC^2 = AC^2, где ^2 — операция возведения в квадрат.
Разделим левую и правую части уравнения на квадрат гипотенузы AC. Тогда предыдущее равенство будет выглядеть так:
АВ^2/AC^2 + BC^2/AC^2 = 1.
Для удобства перепишем равенство, полученное на шаге 2, следующим образом:
(AB/AC)^2 + (BC/AC)^2 = 1.
Согласно определениям, данным на шаге 1, получаем:
cos^2(CAB) + sin^2(CAB) = 1, т.е.
cos(CAB)=SQRT(1-sin^2(CAB)), где SQRT — операция взятия квадратного корня.
Величина синуса и косинуса любого угла не может быть больше 1.
Косинус, как и синус, относят к «прямым» тригонометрическим функциям. Тангенс (вместе с котангенсом) причисляют к другой паре, называемой «производными». Существует несколько определений этих функций, которые делают возможным нахождение тангенса заданного угла по известному значению косинуса от этой же величины.
Есть и еще более экзотический вариант с использованием определения косинуса и тангенса через острые углы прямоугольного треугольника. Косинусу в таком определении соответствует отношение длины прилежащего к рассматриваемому углу катета к длине гипотенузы. Зная значение косинуса можно подобрать соответствующие ему длины этих двух сторон. Например, если cos(α)=0,5, то прилежащий катет можно принять равным 10см, а гипотенузу — 20см. Конкретные числа здесь значения не имеют — одинаковое и правильное решение вы получите с любыми значениями, имеющими такое же соотношение. Затем по теореме Пифагора определите длину недостающей стороны — противолежащего катета. Она будет равна квадратному корню из разницы между длинами возведенных в квадрат гипотенузы и известного катета: √(20²-10²)=√300. Тангенсу по определению соответствует отношение длин противолежащего и прилежащего катетов (√300/10) — рассчитайте его и получите значение тангенса, найденное с использованием классического определения косинуса.
При наличии доступа в интернет используйте онлайн-сервисы, которые размещают на своих страницах калькуляторы тригонометрических функций. Например, перейдите на страницу http://planetcalc.ru/307/ и в поле «Угол» введите величину угла, тангенс которого требуется определить. Если это значение дано не в градусах, а в радианах, градах, угловых минутах или секундах, поставьте отметку в соответствующем поле. Затем нажмите оранжевую кнопку «Рассчитать», и скрипты сервиса произведут необходимые вычисления. Ответ прочтите в поле «Значение» строки «Тангенс» из таблицы, размещенной ниже оранжевой кнопки отправки данных. Кроме тангенса в этой таблице можно увидеть значения еще десяти тригонометрических функций, соответствующих введенному углу. Если доступа в интернет нет, можно использовать программу-калькулятор, входящую в состав операционной системы Windows. Для ее запуска нажмите клавишу Win, введите пару букв названия программы — «ка» — и нажмите Enter. Внутренняя поисковая система найдет и запустит нужное приложение. В версиях, выпущенных раньше, чем такой механизм поиска был встроен в главное меню ОС (например, Windows XP), используйте для запуска пункт «Выполнить» в том же меню — введите в окошко диалога calc и кликните по кнопке OK.
Переключите интерфейс из режима «Обычный» в «Инженерный» — нажмите «горячие клавиши» Alt + 2 или выберите пункт с названием этого режима в разделе «Вид» меню калькулятора.
Наберите величину угла, тангенс которого требуется определить. По умолчанию калькулятор считает введенное значение градусной мерой, но если вам оно дано в радианах или градах, поставьте соответствующую отметку под основным окошком калькулятора. Затем нажмите кнопку, помеченную надписью tan, и программа рассчитает и отобразит результат с точностью до 32 знаков после запятой. Его можно скопировать простым нажатием клавиш Ctrl + C, чтобы затем использовать по своему усмотрению.
Одной из фундаментальных основ точных наук является понятие о тригонометрических функциях. Они определяют простые отношения между сторонами прямоугольного треугольника. К семейству данных функций относится синус. Найти его, зная угол, можно большим количеством способов, включающих экспериментальные, вычислительные методы, а также использование справочной информации.
Используйте калькулятор с функцией вычисления синуса для получения нужных значений на основании знания угла. Подобный функционал сегодня имеют даже самые простые устройства. При этом вычисления производятся с очень высокой степенью точности (как правило, до восьми и более знаков после запятой).
Примените программное обеспечение, представляющее собой среду для работы с электронными таблицами, запущенное на персональном компьютере. Примерами подобных приложений являются Microsoft Office Excel и OpenOffice.org Calc. Введите в любую ячейку формулу, состоящую из вызова функции вычисления синуса с нужным аргументом. Нажмите Enter. В ячейке отобразится искомая величина. Преимуществом электронных таблиц является возможность быстрого расчета значений функций для большого набора аргументов.
Узнайте приближенное значение синуса угла из таблиц Брадиса, если они имеются в наличии. Их недостатком является точность значений, ограниченная четырьмя знаками после запятой.
Найдите приближенное значение синуса угла, совершив геометрические построения. На листе бумаги вычертите отрезок. При помощи транспортира отложите от него угол, синус которого необходимо найти. Начертите еще один отрезок, пересекающий первый в некоторой точке. Перпендикулярно первому же отрезку проведите прямую линию, пересекающую два уже существующих отрезка. Получится прямоугольный треугольник. Измерьте длину его гипотенузы и катета, противолежащего углу, построенному при помощи транспортира. Разделите второе значение на первое. Это и будет искомая величина.
Рассчитайте синус угла, используя разложение в ряд Тейлора. Если значение угла представлено в градусах, переведите его в радианы. Используйте формулу вида: sin(х) = х — (х^3)/3! + (х^5)/5! — (х^7)/7! + (х^9)/9! — … Для повышения скорости расчетов записывайте текущее значение числителя и знаменателя последнего члена ряда, производя вычисление следующего значения на основе предыдущего. Увеличивайте длину ряда для получения более точной величины.
Как из косинуса получить тангенс
1) Определить четверть угла (примерно), а из неё знак синуса 2) sin^2 a + cos^2 a = 1, отсюда найти синус (интегралы-то зачем? квадратного корня хватит) 3) tg a = sin a / cos a
вот ты не умничай, а купи у меня таблицы Брадиса и логарифмическую линейку.. и не говори мне, что не знаешь, что это такое…
тангенс от арккосинуса
как найти синус и косинус если знаем тангенс и катангенс? плиз помогите
Синус и косинус можно будет узнать с точностью до знака из соотношений: 1+tg²x = 1/cos²x 1+ctg²x = 1/sin²x Отсюда cos(x) = ±1/√(1+tg²x) sin(x) = ±1/√(1+ctg²x) При этом знаки у синуса и косинуса должны быть согласованы: если тангенс или котангенс положительны, то синус и косинус имеют одинаковый знак; а если тангенс или котангенс отрицательны, то знаки синуса и косинуса противоположны.
В таблице тригонометрических величин за среднюю школу
tg(x) = sin(x)/cos(x) sin^2(x) = 1-cos^2(x) tg^2(x) = (1 — cos^2(x))/cos^2(x) = 1/cos^2(x) — 1 tg^2(x)*cos^2(x) = 1 — cos^2(x) cos^2(x)*(tg^2(x) + 1) = 1 cos^2(x) = 1/(tg^2(x) + 1) cos(x) = sqrt(1/(tg^2(x) + 1) с синусом все абсолютно аналогично, только проще через котангенс считать.
Источники информации:
- http://shkolkovo.net/theory/26
- http://cos-cos.ru/ege/zadacha209/361/
- http://skysmart.ru/articles/mathematic/formuly-privedeniya
- http://skysmart.ru/articles/mathematic/osnovnoe-trigonometricheskoe-tozhdestvo
- http://reshator.com/sprav/algebra/10-11-klass/preobrazovaniya-grafikov-trigonometricheskih-funkcij/
- http://prosto-o-slognom.ru/matematika/054-formuly_privedeniya.html
- http://xn—-8sbanwvcjzh9e.xn--p1ai/raznoe/kak-iz-kosinusa-perevesti-v-sinus-sin-cos.html
- http://youclever.org/book/formuly-trigonometrii-1/
- http://xn—-8sbanwvcjzh9e.xn--p1ai/raznoe/kak-iz-kosinusa-poluchit-sinus-sin-cos.html