Как из неправильной дроби сделать смешанное число

Смешанные дроби или смешанные числа.

Смешанные дроби в математике можно получить одним из способов, например, из неправильной дроби или путем сложения дробей и еще много вариантов, когда вы сможете столкнуться со смешанной дробью.

Как сделать из неправильной дроби правильную дробь?

Рассмотрим неправильную дробь \(\frac<21><9>\)

Дробная черта — это деление, поэтому число 21 поделим на 9 столбиком.

После деления столбиком у нас появились неполное частное, его записываем в целую часть дроби. Остаток записываем в числитель, а делитель записываем в знаменатель.

Получаем дробь \(2\frac<3><9>\), такие дроби называются смешанными. В этой смешанной дроби число 2 – целая часть, а \(\frac<3><9>\) – правильная дробь.

Смешанные дроби состоят из целой и дробной части.

Рассмотрим еще одну неправильную дробь \(\frac<76><5>\)

Разделим ее столбиком:

Получили смешанную дробь \(15\frac<1><5>\)

Как смешанную дробь перевести в неправильную дробь?

Чтобы из смешанной дроби сделать неправильную дробь нужно знаменатель умножить на целую часть и сложить с числителем, получим числитель неправильной дроби. А знаменатель остается без изменения. Рассмотрим пример:

Вопросы по теме:
Смешанная дробь может быть меньше единицы?
Ответ: нет, потому что смешанную дробь можно представить в виде неправильной дроби, а неправильная дробь всегда больше или равна единицы.

Что показывает целая часть у смешанной дроби?
Ответ: целая часть показывает сколько полных знаменателей содержит дробь.

Как представить смешанное число в виде неправильной дроби?
Ответ: к произведению знаменатели и целой части прибавить числитель получим числитель искомой неправильной дроби, а знаменатель не меняется.

Как перевести неправильную дробь в смешанное число? И как выделить целую часть?
Ответ: делим в столбик числитель на знаменатель, неполное частное – это целое, делитель – это знаменатель, а остаток – это числитель. Смотрите пример выше.

Что такое смешанные дроби или смешанные числа?
Ответ: Смешанные дроби – это числа, которые состоят из целой и дробной части.

Пример №1:
Представьте дробь в виде смешанного числа: \(\frac<508><17>\)

Решение:
Разделим дробь столбиком:

Ответ: Получили смешанную дробь \(29\frac<15><17>\)

Пример №2:
Представьте число в виде неправильной дроби: а) \(9\frac<2><3>\), б) \(1\frac<3><7>\)
Решение:
а) \(9\frac<2> <3>= \frac<9 \times 3 +2> <3>= \frac<29><3>\\\\\)
б) \(1\frac<3> <7>= \frac<1 \times 7 +3> <7>= \frac<10><7>\\\\\)

Задача №1:
Миша готовился к экзамену. За месяц он решил 120 задач. За первую неделю Миша решил \(\frac<2><5>\) от этого числа. Сколько задач решил Миша за первую неделю?

Решение:
У нас есть дробь \(\frac<2><5>\), знаменатель равен 5 это значит, что общее число 120 надо разделить на 5 и получим сколько составляет одна часть.
\(120 \div 5 = 24\) задачи это одна часть или \(\frac<1><5>\)
В числителе стоит 2, значит нам надо взять две части, поэтому 24 умножаем на 2.
\(24 \times 2 = 48\) задач
Ответ: за неделю Миша решил 48 задач.

Смешанные числа, перевод смешанного числа в неправильную дробь и обратно

В этом материале мы разберем такое понятие, как смешанные числа. Начнем, как всегда, с определения и небольших примеров, потом поясним связь смешанных чисел и неправильных дробей. После этого мы изучим, как правильно выделять целую часть из дроби и получать в результате целое число.

Понятие смешанного числа

Числа вида 0 3 14 также не относятся к смешанным. Здесь не выполняется первая часть условия: целая часть должна быть представлена только натуральным числом, а нуль им не является.

Как соотносятся между собой неправильные дроби и смешанные числа

Эту связь проще всего проследить на конкретном примере.

Наш пример доказывает, что в виде смешанного числа можно представить любую неправильную дробь.

Мы поняли, как приводить неправильную дробь к виду смешанного числа. Если в числителе неправильной дроби стоит такое число, которое можно разделить на знаменатель без остатка, то можно сделать это, и тогда наша неправильная дробь станет натуральным числом.

Как перевести смешанное число в неправильную дробь

Чтобы успешно решать задачи, полезно уметь производить и обратное действие, то есть делать из смешанных чисел неправильные дроби. В этом пункте мы разберем, как правильно это сделать.

Для этого нужно воспроизвести следующую последовательность действий:

1. Для начала представляем имеющееся смешанное число n a b как сумму целой и дробной части. Получается n + a b

2. Далее заменяем целую часть на дробь со знаменателем, равным единице (то есть записываем n как n 1 ).

Разберем это действие на конкретном примере.

Представьте 5 3 7 в виде неправильной дроби.

Решение

Последний шаг – сложение дробей, имеющих разные знаменатели:

5 1 + 3 7 = 35 7 + 3 7 = 38 7

Представьте 15 2 5 в виде неправильной дроби.

Решение

Как выделить из неправильной дроби целую часть

Обычно мы не указываем неправильную дробь в качестве итогового ответа. Принято доводить вычисления до конца и заменять ее либо натуральным числом (разделив числитель на знаменатель), либо смешанным числом. Как правило, первый способ используется, когда разделить числитель на знаменатель можно без остатка, а второй – если такое действие невозможно.

Когда мы выделяем из неправильной дроби целую часть, мы просто заменяем ее равным смешанным числом.

Разберем, как именно это делается.

Приведем доказательство этого утверждения.

Выделение целой части из неправильной дроби a b осуществляется таким образом:

1) производим деление a на b с остатком и записываем неполное частное q и остаток r отдельно.

Представьте 107 4 в виде смешанного числа.

Решение

Делим 104 на 7 столбиком:

Нам осталось посмотреть, как заменить неправильную дробь натуральным числом (при условии, что ее числитель делится на знаменатель без остатка).

Как перевести смешанную дробь в неправильную и наоборот

Объяснения с примерами

Как перевести смешанную дробь в неправильную

Смешанная дробь — это запись целого числа с обыкновенной дробью.

Читается 5 целых три восьмых.

Чтобы нагляднее себе представить, можно мысленно добавлять знак «+» между целым числом и обыкновенной дробью. И это не будет ошибкой, так как знак «плюс» для упрощения записи опускается.

Эта запись означает 5 целых пирогов и 3 восьмых пирога.

5 площадей определенных размеров и 3 восьмых данной площади.

Неправильная дробь — эта та, у которой числитель больше знаменателя. Соответственно, из неё можно выделить 1 целое число или больше. Так как любая неправильная дробь больше единицы.

Можно сделать действие и наоборот — превратить смешанное число в неправильную дробь.

Чтобы перевести смешанное число в неправильную дробь нужно целое число умножить на знаменатель и прибавить числитель. Полученное значение записываем в числитель. Знаменатель оставляем без изменений.

Объяснение почему именно так мы переводим:

Целое число мы можем записать дробью, как сорок восьмых (40: 8 = 5). Не забывайте, что дробь — это деление. Число 40 мы получаем умножением целого числа на знаменатель. Теперь нам осталось сложить две дроби с одинаковыми знаменателями.

Примеры для перевода смешанных дробей в неправильные

Как перевести неправильную дробь в смешанную

Как мы уже говорили, неправильная дробь всегда больше единицы.

Чтобы перевести неправильную дробь в смешанную нужно начать делить числитель на знаменатель до целых. Полученное целое число пишем перед дробью, остаток деления — в числитель. Знаменатель остаётся без изменения.

Схема для запоминания:

Примеры

Как перевести неправильную дробь в правильную

Смешанную дробь иногда называют правильной, поэтому объяснение перевода будет являться дублированием предыдущего абзаца. Если у вас остались вопросы, то смотрите разбор в видео:

Смешанные числа

Содержание

На этом уроке мы разберём, что такое смешанное число, узнаем, как перевести неправильную дробь в смешанное число и наоборот, из смешанного числа сделать неправильную дробь.

Знакомство со смешанными числами

А что будет, если мы будем делить на четверых 5 яблок?

Можно так же разрезать каждое яблоко на 4 кусочка, и каждый возьмёт 5 четвертинок. Но обычно делают не так.

Читается это как «Одна целая одна четвёртая». Подобную запись (целое число и дробь) называют «смешанной», а само число – «смешанным числом». Запись числа, содержащую целую и дробную части, называют смешанной.

Как перевести неправильную дробь в смешанное число

Как думаете, из любой дроби можно сделать смешанное число?

Нет, только из неправильной дроби. В правильной дроби просто «не хватает» долей числа на то, чтобы из них получилась целая часть.

Нужно разделить 11 на 5, 11 на 5 не делится, берём ближайшее число – 10.

Чтобы из неправильной дроби выделить целую часть, надо:
1) разделить числитель на знаменатель
2) если деление произошло без остатка, результатом будет целое число, если же деление прошло с остатком, то неполное частное будет целой частью. Остаток становится числителем, а делитель — знаменателем дробной части.

Превращение смешанной дроби в неправильную дробь

А если нам нужно, наоборот, превратить смешанную дробь в неправильную?

Сначала нам нужно представить целую часть в виде дроби с таким же знаменателем, как у дробной части, а потом сложить получившуюся дробь с дробной частью.

Разберём на примере.

Чтобы представить смешанное число в виде дробной части, надо:
1) умножить целую часть дроби на знаменатель дробной части
2) прибавить получившееся произведение к числителю дробной части. Знаменатель оставить без изменения.

Буквами это можно записать так:

Лена, Марина и Никита делили несколько шоколадок поровну: каждому дали по шоколадке, а оставшуюся лишнюю разделили на 3 части. Но Никита сказал, что шоколадки-то одинаковые по размеру, но что, если они все с разными вкусами? Честнее и интереснее будет разломить каждую шоколадку на 3 части, а потом каждый возьмёт себе равное количество частей.

Можете сказать, сколько частей шоколадки было у каждого? А сколько всего частей шоколадок у них получилось? И сколько целых шоколадок было в начале?

Получается, что каждый взял по 4 части.

А когда шоколадки разломили на кусочки, сколько получилось?

То есть у них получилось 12 третьих частей шоколадки.

Смешанные числа, перевод смешанного числа в неправильную дробь и обратно.

В этой статье мы поговорим про смешанные числа. Сначала дадим определение смешанных чисел и приведем примеры. Дальше остановимся на связи между смешанными числами и неправильными дробями. После этого покажем, как перевести смешанное число в неправильную дробь. Наконец, изучим обратный процесс, который называется выделением целой части из неправильной дроби.

Навигация по странице.

Смешанные числа, определение, примеры

Так мы подошли к определению смешанного числа.

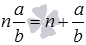
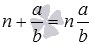
По определению смешанное число равно сумме свой целой и дробной части, то есть, справедливо равенство , которое можно записать и так: .

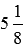
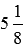
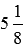
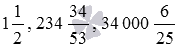
Приведем примеры смешанных чисел. Число — это смешанное число, натуральное число 5 – целая часть числа , а — дробная часть числа . Другими примерами смешанных чисел являются .

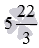
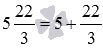
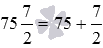
Иногда можно встретить числа в смешанной записи, но имеющие дробной частью неправильную дробь, например, или . Эти числа понимают как сумму их целой и дробной части, например, и . Но такие числа не подходят под определение смешанного числа, так как дробной частью смешанных чисел должна быть правильная дробь.

Число — это тоже не смешанное число, так как 0 не натуральное число.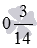

Связь между смешанными числами и неправильными дробями

Проследить связь между смешанными числами и неправильными дробями лучше всего на примерах.

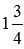
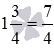
Пусть на подносе лежит торт и еще 3/4 такого же торта. То есть, по смыслу сложения на подносе находится 1+3/4 торта. Записав последнюю сумму в виде смешанного числа, констатируем, что на подносе находится торта. Теперь целый торт разрежем на 4 равные доли. В результате на подносе окажется 7/4 торта. Понятно, что «количество» торта при этом не изменилось, поэтому .

Из рассмотренного примера явно видна такая связь: любое смешанное число можно представить в виде неправильной дроби.

Из этого примера понятно, что неправильную дробь можно представить в виде смешанного числа. (В частном случае, когда числитель неправильной дроби делится нацело на знаменатель, неправильную дробь можно представить в виде натурального числа, например, 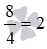, так как 8:4=2 ).

Перевод смешанного числа в неправильную дробь

Для выполнения различных действий со смешанными числами оказывается полезным навык представления смешанных чисел в виде неправильных дробей. В предыдущем пункте мы выяснили, что любое смешанное число можно перевести в неправильную дробь. Пришло время разобраться, как осуществляется такой перевод.

Рассмотрим пример перевода смешанного числа в неправильную дробь.

Представьте смешанное число 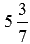в виде неправильной дроби.

Выполним все необходимые шаги алгоритма.

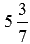
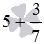
Смешанное число равно сумме его целой и дробной части: .

Чтобы закончить перевод исходного смешанного числа в неправильную дробь, осталось выполнить сложение дробей с разными знаменателями: .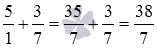

Краткая запись всего решения такова: .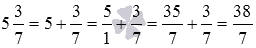

.

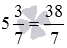
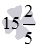
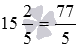
Запишите смешанное число в виде неправильной дроби.

.

Выделение целой части из неправильной дроби

В ответе не принято записывать неправильную дробь. Неправильную дробь предварительно заменяют либо равным ей натуральным числом (когда числитель делится нацело на знаменатель), либо проводят так называемое выделение целой части из неправильной дроби (когда числитель не делится нацело на знаменатель).

Выделение целой части из неправильной дроби – это замена дроби равным ей смешанным числом.

Осталось узнать, как можно выделить целую часть из неправильной дроби.

Докажем это утверждение.

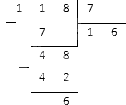
Рассмотрим решение примера.

Выполним деление столбиком:

Таким образом, неправильная дробь 118/7 равна смешанному числу .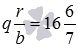

.

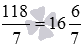
Как неправильную дробь превратить в смешанное число?

Любую неправильную дробь можно превратить в смешанное число. Для этого числитель дроби разделим на знаменатель. Получится целое число и остаток. Число — это целая часть дроби. Остаток – это числитель дроби. А знаменатель остается тем же, т.е число на которое мы делили.
Давайте разбираться.
1.

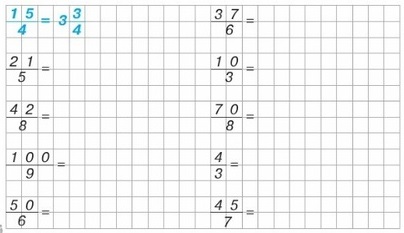
3. Давайте потренируемся:

Проверка: 15 / 4 — это 15 : 4. 15 на 4 не делится нацело: делим 12 на 4 = 3, значит, 3 целых. Находим дробь: 15 – 12 = 3, т.е. осталось 3 – это числитель, т.е. три четвертых, потому что мы делим на 4.
21/5 — это 21 : 5. 21 на 4 не делится нацело: делим 20 на 5 = 4, значит, 4 целых. Находим дробь: 21 – 20 = 1, т.е. осталось 1 – это числитель дроби, т.е. одна пятая, потому что мы делим на 5.
42/8 – это 42 : 8. 42 на 8 не делится нацело: делим 40 на 8 = 5, значит, 5 целых. Находим дробную часть: 42 – 40 = 2, т.е. осталось 2 – это числитель дроби, т.е. две восьмых, потому что мы делим на 8.
100/9 – это 400 : 9. 100 на 9 не делится нацело: делим 99 на 9 = 11, значит, 11 целых. Находим дробную часть: 100 – 99 = 1, т.е. осталось 1 – это числитель дроби, т.е. одна девятая, потому что мы делим на 9.
50/6 – это 50 : 6. 50 на 6 не делится нацело: делим 48 на 6 = 8, значит, 8 целых. Находим дробную часть: 50 – 48 = 2, т.е. осталось 2 – это числитель дроби, т.е. две шестых, потому что мы делим на 6.
37/6 – это 37 : 6. 37 на 6 не делится нацело: делим 36 на 6 = 6, значит, 6 целых. Находим дробную часть: 37 – 36 = 1, т.е. осталось 1 – это числитель дроби, т.е. одна шестая, потому что мы делим на 6.
10/3 – это 10 : 3. 10 на 3 не делится нацело: делим 9 на 3 = 3, значит, 3 целых. Находим дробную часть: 10 – 9 = 1, т.е. осталось 1 – это числитель дроби, т.е. одна третья, потому что мы делим на 3.
70/8 – это 70 : 8. 70 на 8 не делится нацело: делим 64 на 8 = 8, значит, 8 целых. Находим дробную часть: 70 – 64 = 6, т.е. осталось 6 – это числитель дроби, т.е. шесть восьмых, потому что мы делим на 8.
4/3 – это 4 : 3. 4 на 4 не делится нацело: делим 3 на 3 = 1, значит, 1 целая. Находим дробную часть: 4 – 3 = 1, т.е. осталось 1 – это числитель, т.е. она третья, потому что мы делим на 3.
45/7 – это 45 : 7. 45 на 7 не делится нацело: делим 42 на 7 = 6, значит, 6 целых. Находим дробную часть: 45 – 42 = 3, т.е. осталось 3 – это числитель, т.е. три седьмых, потому что мы делим на 7.

Урок 38 Бесплатно Смешанные числа

На данном уроке мы продолжим разговор об обыкновенных дробях.

Выясним, какие числа называют смешанными, как их принято записывать и читать.

Установим связь между смешанными числами и правильными дробями.

Научимся переводить смешанное число в неправильную дробь.

Рассмотрим обратную операцию перевода неправильной дроби в смешанное число.

Определим расположение смешанных чисел на координатном луче.

Взаимосвязь между смешанным числом и неправильной дробью

Правильной называют дробь, в которой числитель меньше знаменателя, она всегда меньше единицы.

Неправильной называют дробь, в которой числитель больше знаменателя или равен ему, такие дроби всегда больше единицы.

Сегодня речь пойдет о неправильных дробях.

Рассмотрим несколько примеров.

Пример №1.

Разделили три конфеты на троих человек.

Сколько конфет получил каждый?

Известно, что обыкновенная дробь \(\mathbf<\frac>\) представляет собой математическую операцию деления m— объектов на n-частей, а дробную черту, которая отделяет числитель от знаменателя, применяют как знак деления.

Общее количество конфет (m = 3) разделим на количество человек (n = 3).

Запишем частное в виде дроби.

В результате получили неправильную дробь, в которой числитель равен знаменателю.

\(\mathbf<\frac<3> <3>= 3 \div 3 = 1>\) (конф.) получил каждый.

Ответ: каждый получил 1 конфету.

Пример №2.

Разделили поровну шесть конфет между тремя друзьями.

Сколько конфет получил каждый?

Общее количество конфет (m = 6) разделим на количество друзей (n = 3).

Запишем частное в виде дроби.

В итоге получилась неправильная дробь, в которой числитель больше знаменателя.

\(\mathbf<\frac<6> <3>= 6 \div 3 = 2>\) (конф.) получил каждый из друзей.

Ответ: по 2 конфеты получил каждый из друзей.

В рассмотренных примерах частное двух чисел найти было нетрудно, так как числитель дроби нацело делится на знаменатель.

Рассмотрим еще одну ситуацию.

Пример №3.

Два брата решили разделить поровну пять апельсинов.

Сколько апельсинов достанется каждому из братьев?

Общее количество апельсинов (m = 5) разделим на количество братьев (n = 2).

Запишем частное в виде дроби.

В данном примере мы получили неправильную дробь, в которой числитель хоть и больше знаменателя, но он не делится нацело.

Разделить пять апельсинов на две равные части можно двумя способами.

1. Можно разрезать каждый апельсин на две равные части.

Каждая полученная часть будет равна ½ апельсина.

Тогда по одной части от каждого апельсина достанется каждому из братьев.

Оба мальчика получат по пять таких частей: \(\mathbf<\frac<1> <2>+ \frac<1> <2>+ \frac<1> <2>+ \frac<1> <2>+ \frac<1><2>>\)

Следовательно, каждый получит \(\mathbf<\frac<5><2>>\) апельсина.

Если внимательно присмотреться к сумме дробей, можно заметить, что две части, т.е. сумма \(\mathbf<\frac<1> <2>+ \frac<1><2>>\) составляет \(\mathbf<\frac<2><2>>\).

В свою очередь нам известно, что неправильная дробь \(\mathbf<\frac<2><2>>\) равна единице: \(\mathbf<\frac<2> <2>= 2 \div 2 = 1>\).

Таким образом получится, что каждому мальчику достанется два апельсина, да еще половинка: \(\mathbf<2 + \frac<1><2>>\) апельсина.

2. Можно поделить поровну сначала целые апельсины.

В таком случае каждому брату достанется по два апельсина.

Затем оставшийся апельсин необходимо разделить поровну на двоих, так каждый получит еще по половине апельсина, т.е. (\(\mathbf<\frac<1><2>>\)) его часть.

В результате оба брата получат по два целых апельсина, да еще половину: \(\mathbf<2 + \frac<1><2>>\) апельсина.

Сумму \(\mathbf>\), где А— это натуральное число, \(\mathbf<\frac>\)— правильная дробь, можно записать в виде \(\mathbf>\).

Такую сокращенную запись называют смешанным числом, оно имеет целую часть (натуральное число) и дробную часть (дробное число).

Дробная часть смешанного числа- это всегда правильная дробь.

Например, представим смешанные числа в виде суммы их целой и дробной части.

\(\mathbf<1\frac<4> <11>= 1 + \frac<4><11>>\) (целая часть равна 1, дробная- \(\mathbf<\frac<4><11>>\)).

\(\mathbf<7\frac<10> <15>= 7 + \frac<10><15>>\) (целая часть равна 7, дробная- \(\mathbf<\frac<10><15>>\)).

\(\mathbf<\frac<5> <16>= 0 + \frac<5><16>>\) (целая часть отсутствует, т.е. равна 0, дробная- \(\mathbf<\frac<5><16>>\)).

А теперь наоборот сумму натурального числа и правильной дроби представим в виде смешанного числа.

Выразим в килограммах 3 килограмма 150 граммов.

Известно, что 1 кг = 1000 г.

Значит 150 г- это часть от килограмма, т.е. часть от 1000 г.

Чтобы узнать какую часть составляет 150 г от 1000 г, необходимо 150 разделить на 1000, получим \(\mathbf<\frac<150><1000>>\).

В итоге имеем 3 килограмма, да еще часть- \(\mathbf<\frac<150><1000>>\) килограмма, получаем \(\mathbf<3 + \frac<150><1000>>\).

Ответ: 3 килограмма 150 граммов- это \(\mathbf<3\frac<150><1000>>\) килограмма.

Число, содержащее целую часть (натуральное число) и дробную часть (правильную дробь), называют смешанным числом.

Читают смешанное число следующим образом: произносится сначала целая часть, затем дробная, в соответствии с правилами чтения дробных чисел.

В нашем примере про апельсины выражение \(\mathbf<2 + \frac<1><2>>\) можно записать как \(\mathbf<2\frac<1><2>>\).

Число 2— это целая часть смешанного числа, а число \(\mathbf<\frac<1><2>>\) его дробная часть.

Читается данное число так: «Две целых одна вторая».

Любое смешанное число можно перевести в неправильную дробь.

Выясним взаимосвязь смешанных чисел и неправильных дробей на примере.

Испекли три одинаковые пиццы.

От первой пиццы съели несколько кусочков, в результате от нее осталась часть, равная \(\mathbf<\frac<5><8>>\) всей пиццы.

По сути осталось несъеденными 2 (две) целых да еще \(\mathbf<\frac<5><8>>\) (пять восьмых) пиццы.

Если мы сложим эти два числа, то получим сумму \(\mathbf<2 + \frac<5><8>>\).

Выражение \(\mathbf<2 + \frac<5><8>>\) представляет собой ничто иное, как смешанное число \(\mathbf<2\frac<5><8>>\) (две целых пять восьмых).

Общее количество оставшейся пиццы мы можем определить иначе.

Возьмем так же три одинаковые пиццы и разрежем каждую на восемь равных частей.

Теперь вторую и третью пиццу мы можем представить в виде дроби \(\mathbf<\frac<8><8>>\), а остаток от первой запишем как \(\mathbf<\frac<5><8>>\).

В результате общее количество несъеденной пиццы будет выражаться суммой:

При этом ясно, что общее количество оставшейся пиццы, найденное первым способом и вторым, совпадают, значит \(\mathbf<2\frac<5> <8>= \frac<21><8>>\).

Запишем алгоритм перевода смешанного числа в неправильную дробь.

Чтобы представить смешанное число в виде неправильной дроби, необходимо:

1. Умножить целую часть смешанного числа на знаменатель его дробной части.

2. К полученному произведению прибавить числитель дробной части.

3. Записать полученный результат суммы в числитель новой дроби.

4. Знаменатель оставить без изменений.

У меня есть дополнительная информация к этой части урока!

В буквенном виде перевод смешанного числа в неправильную дробь можно записать следующим образом:

Пусть А— целя часть смешанного числа.

\(\mathbf<\frac>\)- дробная часть смешанного числа.

Рассмотрим несколько примеров.

Пример №1.

Представьте смешанное число \(\mathbf<6\frac<2><5>>\) в виде дроби.

1. Умножим целую часть смешанного числа (число 6) на знаменатель его дробной части (число 5), получим число 30.

6 • 5 = 30

2. К полученному произведению (число 30) прибавим числитель дробной части смешанного числа (число 2), получим число 32.

3. Запишем полученную сумму (число 32) в числитель новой дроби, а знаменатель останется прежним (число 5).

Получили неправильную дробь \(\mathbf<\frac<32><5>>\).

Пример №2.

Представьте смешанное число \(\mathbf<20\frac<1><3>>\) в виде дроби.

Умножим целую часть смешанного числа на знаменатель его дробной части, к полученному произведению прибавим числитель дробной части, запишем полученный результат суммы в числитель новой дроби, а знаменатель оставим без изменений.

Получили неправильную дробь \(\mathbf<\frac<61><3>>\).

Пример №3.

Представьте смешанное число \(\mathbf<3\frac<3><4>>\) в виде дроби.

Умножим целую часть смешанного числа на знаменатель его дробной части, к полученному произведению прибавим числитель дробной части, запишем полученный результат суммы в числитель новой дроби, а знаменатель оставим без изменений.

Получили неправильную дробь \(\mathbf<\frac<15><4>>\).

Возможна и обратная операция.

Неправильную дробь, в которой числитель нацело не делится на знаменатель, можно представить в виде смешанного числа.

Чтобы перейти от неправильной дроби к смешенному числу, необходимо выделить целую часть.

Выделить целую часть из неправильной дроби- это значит заменить неправильную дробь равным ей смешанным числом.

Для этого необходимо разделить с остатком числитель неправильной дроби на знаменатель.

При этом неполное частное будет являться целой частью, остаток- числителем, а делитель- знаменателем.

Знаменатель неправильной дроби всегда равен знаменателю дробной части смешенного числа.

Запишем алгоритм выделения целой части из неправильной дроби.

Чтобы перейти от неправильной дроби к смешанному числу, необходимо:

1. Разделить с остатком числитель неправильной дроби на ее знаменатель.

2. Неполное частное будет представлять собой целую часть смешанного числа.

3. Если остаток есть, то его необходимо записать в числитель дробной части смешанного числа, а делитель в знаменатель.

У меня есть дополнительная информация к этой части урока!

На примере рассмотрим перевод неправильной дроби в смешанное число.

Выделим целую часть из неправильной дроби \(\mathbf<\frac<37><8>>\).

Давайте выполним деление с остатком в столбик («деление уголком»).

Наибольшее число, которое меньше 37 и делится на 8— это 32.

32 разделим на делитель 8, получим 4-это неполное частное.

Вычтем из делимого числа 37 найденное наибольшее число 32, получим число 5— это остаток от деления.

По-другому деление с остатком можно записать так 37 ÷ 8 = 4 ( ост. 5 ).

В результате получим смешанное число \(\mathbf<4\frac<5><8>>\), в котором 4— целая часть, \(\mathbf<\frac<5><8>>\)- дробная часть.

Пройти тест и получить оценку можно после входа или регистрации

Смешанные числа на координатном луче

Выясним, где на координатном луче находятся смешанные числа.

1. Для того чтобы изобразить на координатном луче смешанное число, важно выбрать правильно длину единичного отрезка.

Единичный отрезок целесообразно устанавливать такой длины, чтобы было удобно его разделить на части, количество которых должно соответствовать числу, стоящему в знаменателе.

2. Далее от начала отсчета нужно отложить определенное количество равных частей, соответствующих числу, стоящему в числителе.

Рассмотрим поясняющий пример.

Отметим на координатном луче точку с координатой \(\mathbf<2\frac<2><3>>\).

\(\mathbf<2\frac<2><3>>\)— это смешанное число.

Данное смешанное число содержит правильную дробь со знаменателем 3.

Следовательно, единичный отрезок разобьем на три равные части, каждая такая часть (доля) будет равна \(\mathbf<\frac<1><3>>\) единичного отрезка.

Изобразим горизонтальный координатный луч, направленный вправо, с началом отсчета в точке О(0) и единичным отрезком ОЕ, равным 1 единице.

В таком случае одна часть (доля единичного отрезка) соответствует дроби \(\mathbf<\frac<1><3>>\), две части- это \(\mathbf<\frac<2><3>>\), три части- это 1.

Чтобы изобразить смешанное число \(\mathbf<2\frac<2><3>>\), отсчитываем от начала координат два целых единичных отрезка, а от третьего единичного отрезка возьмем только две его доли из трех.

Отметим точку на координатном луче, назовем ее точка А(\(\mathbf<2\frac<2><3>>\)).

Переведем смешанное число в неправильную дробь.

Определим расположение точки с координатой \(\mathbf<\frac<8><3>>\).

Дробь \(\mathbf<\frac<8><3>>\) означает восемь долей единичного отрезка ОЕ.

Отложим от начала координат восемь долей, каждая из которых равна \(\mathbf<\frac<1><3>>\) единичного отрезка.

Попадем в точку с координатой \(\mathbf<\frac<8><3>>\).

В этой же точке мы ранее отметили точку А(\(\mathbf<2\frac<2><3>>\)).

Смешанное число и соответствующая ему неправильная дробь, у которой числитель больше знаменателя, на координатном луче находятся всегда правее единицы и принадлежат они одной и той же точке координатного луча.

Определим расположение точек В(\(\mathbf<1\frac<2><3>>\)), С(\(\mathbf<2\frac<1><3>>\)), D(\(\mathbf<\frac<12><3>>\)) на координатном луче.

Изобразим горизонтальный координатный луч, направленный вправо, с началом отсчета в точке О(0) и единичным отрезком ОЕ, равным 1 единице.

Так как знаменатель каждой заданной дроби равен трем, то разобьем единичный отрезок ОЕ на три равные части, каждая часть будет равна \(\mathbf<\frac<1><3>>\) ОЕ.

1. Смешанное число \(\mathbf<1\frac<2><3>>\) представляет собой один целый единичный отрезок, да еще две части (доли) из трех от второго единичного отрезка.

Следовательно, точка В(\(\mathbf<1\frac<2><3>>\)) будет удалена вправо от начала координат на расстояние одного целого единичного отрезка, да еще двух отрезков, каждый из которых равен одной доле единичного отрезка.

В данную точку также мы можем попасть, если от начала координат вправо отсчитаем пять долей единичного отрезка- (\(\mathbf<\frac<5><3>>\))ОЕ.

Таким образом точка с координатой \(\mathbf<\frac<5><3>>\) и точка с координатой \(\mathbf<1\frac<2><3>>\) это одна и та же точка на координатном луче.

Отметим тот факт, что \(\mathbf<1\frac<2><3>>\) смешанное число и соответствующая ему неправильная дробь \(\mathbf<\frac<5><3>>\) больше единицы, и на координатном луче данные точки располагаются правее единицы (правее точки E(1)).

2. Выясним, где на координатном луче будет находиться точка С(\(\mathbf<2\frac<1><3>>\)).

Смешанное число \(\mathbf<2\frac<1><3>>\) представляет собой два целых единичных отрезка, да еще одну часть (долю) из трех от третьего единичного отрезка.

Отметим точку С(\(\mathbf<2\frac<1><3>>\)) на координатном луче, для этого отсчитаем вправо от начала координат два целых единичных отрезка и еще одну долю единичного отрезка, равную \(\mathbf<\frac<1><3>>\) ОЕ.

Так же в данную точку можно попасть, если от начала координат вправо отсчитать семь долей единичного отрезка- (\(\mathbf<\frac<7><3>>\))OE.

Точка с координатой \(\mathbf<\frac<7><3>>\) и точка с координатой \(\mathbf<2\frac<1><3>>\) это одна и та же точка на координатном луче.

Смешанное число \(\mathbf<2\frac<1><3>>\) и соответствующая ему неправильная дробь \(\mathbf<\frac<7><3>>\) больше единицы, на координатном луче данные точки располагается правее единицы (правее точки E(1)) и правее найденной нами точки В(\(\mathbf<1\frac<2><3>>\)).

3. Обозначим на координатном луче точку D с координатой \(\mathbf<\frac<12><3>>\).

\(\mathbf<\frac<12><3>>\)- неправильная дробь, в которой числитель больше знаменателя.

Найдем соответствующее этой дроби смешанное число, для этого выделим из дроби \(\mathbf<\frac<12><3>>\) целую часть.

Получается, что дробь \(\mathbf<\frac<12><3>>\) равна четырем целым единичным отрезкам.

Дробная часть данного числа отсутствует, т.е. она равна нулю.

\(\mathbf<\frac<12><3>>\) и 4— это одно и то же число, значит \(\mathbf<\frac<12> <3>= 4>\).

Отложим от начала координат четыре целых единичных отрезка и обозначим точку D(\(\mathbf<\frac<12><3>>\)).

Обратите внимание как расположены смешанные числа на координатном луче, чем правее от единицы находится смешанное число, тем оно больше.

Пройти тест и получить оценку можно после входа или регистрации

Как преобразить неправильную дробь в смешанное число. Смешанные числа, перевод смешанного числа в неправильную дробь и обратно

Огромный блок математики посвящен работе с дробями или нецелыми числами. С ними очень часто встречаются и в жизни, поэтому знать, как работать с такими цифрами важно для любого человека. Математика – это наука, в которой ученик начинает с познания простых вещей и действий, а затем переходит к более сложным.

Знание и умение работать с подобными цифрами облегчит ему в дальнейшем работу с логарифмами, рациональными показателями и интегралами. С такими числами можно делать все то же самое, что и с обыкновенными: складывать дроби, делить, вычитать и умножать. Кроме этого, их можно сокращать. Работать с дробями просто, главное – это знать основные правила и методы их вычисления.

Основные понятия

Для того, чтобы понять, что это за значение такое, необходимо представить некий целый предмет. Допустим, что есть торт, который порезали на несколько одинаковых или равных кусков. Каждый кусочек будет называться долей.

Например, 10 состоит из 5 двоек, каждая двойка – это часть от десяти.

Доли имеют свои названия, в зависимости от их общего количества в целом числе: 10 может состоять из двух пятёрок или пяти двоек, в первом случае она будет называться (одна вторая), а во втором — (одна пятая). Следует помнить, что равняется половине числа, (одна третья) — трети, а (одна четвертая) – четвертью. Их могут также изображать через черточку: ½, 1/3 или 1/5.

Цифру, написанную сверху горизонтальной линии или слева от наклонной, называют числителем – он показывает сколько долей взяли у целого числа, а цифра под линии или справа от нее – знаменатель, он показывает на сколько всего долей разделили. Например, торт разделили на 10 кусков и сразу отложили два из них для опоздавших гостей. Это будет 2/10 (две десятых), т.е. взяли 2 (числитель) куска от общих 10 (знаменатель).

Какие бывают доли, что такое неправильная дробь, что такое обыкновенная дробь? На эти вопросы легко ответить:

Смешанная цифра всегда может трансформироваться в неправильную дробь и наоборот.

Главное свойство гласит: при умножении, а также деления делимого и делителя на одинаковый множитель, в целом величина дроби не изменится. Это свойство делает возможным все операции с дробями.

Как сократить?

Сокращать можно при умножении дробных выражений друг на друга:

*. Сами по себе эти числа несократимые, но выполняя операцию умножения, можно сократить их по диагонали: * = =. Сокращать при умножении можно только крест-накрест: числитель первой со знаменателем второй, и наоборот.

Сокращать можно и смешанную цифру, т.е. целую часть и правильную дробь представить в виде неправильной. Для этого следует выполнить некоторые действия:

Справедливо и обратное действие: из неправильной дроби сделать смешанную. Для этого рассмотрим обратное действие с :

Таким способом сокращать дроби при любых операциях возможно. Можно сокращать значения ее делимого и делителя при умножении их на одинаковый множитель, и превращая из смешанного числа в долю, и наоборот.

Возможные действия

Все основные виды вычислений доступны при счете долей, как и с целыми цифрами: сложение, вычитание и прочие. Рассмотрим каждое действие по отдельности с примерами:

Сложение и вычитание

Складывать доли можно двумя путями, в зависимости от их делителя. Они бывают одинаковыми и разными. Рассмотрим пример складывания долей с одинаковыми делителями.

Вычитание осуществляется точно так же: в случае с одинаковыми делителями их не трогаем, а числители последовательно вычитаем: — = =

. Если же знаменатели различные, то следует поступить, как и при сложении: найти НОК, множители, умножить доли, а затем вычесть уже доли с одинаковыми делителями.

Какие виды дробей существуют?

Для начала о том, что это такое. Дробь — число, которое имеет некоторую часть от единицы. Ее можно записать в двух видах. Первый носит название обыкновенной. То есть такая, у которой есть горизонтальная или наклонная черта. Она приравнивается к знаку деления.

В такой записи число, стоящее над черточкой, называется числителем, а под ней — знаменателем.

Среди обыкновенных выделяют правильные и неправильные дроби. У первых числитель по модулю всегда меньше знаменателя. Неправильные потому так и называются, что у них все наоборот. Значение правильной дроби всегда меньше единицы. В то время как неправильная всегда больше этого числа.

Есть еще смешанные числа, то есть такие у которых имеются целая и дробная части.

Второй вид записи — десятичная дробь. О ней отдельный разговор.

Чем отличаются неправильные дроби от смешанных чисел?

По своей сути, ничем. Это просто разная запись одного и того же числа. Неправильные дроби после несложных действий легко становятся смешанными числами. И наоборот.

Все зависит от конкретной ситуации. Иногда в заданиях удобнее использовать неправильную дробь. А порой необходимо перевести ее в смешанное число и тогда пример решится очень легко. Поэтому, что использовать: неправильные дроби, смешанные числа, — зависит от наблюдательности решающего задачу.

Смешанное число еще сравнивают с суммой целой части и дробной. Причем вторая всегда меньше единицы.

Как представить смешанное число в виде неправильной дроби?

Если требуется выполнить какое-либо действие с несколькими числами, которые записаны в разных видах, то нужно сделать их одинаковыми. Один из методов — представить числа в виде неправильных дробей.

Для этой цели потребуется выполнить действия по такому алгоритму:

Вот примеры того, как записать неправильные дроби из смешанных чисел:

Как записать неправильную дробь в виде смешанного числа?

Следующий прием противоположен рассмотренному выше. То есть когда все смешанные числа заменяются на неправильные дроби. Алгоритм действий будет таким:

Примеры такого преобразования:

76/14; 76:14 = 5 с остатком 6; ответом будет 5 целых и 6/14; дробную часть в этом примере нужно сократить на 2, получится 3/7; итоговый ответ — 5 целых 3/7.

108/54; после деления получается частное 2 без остатка; это значит, что не все неправильные дроби удается представить в виде смешанного числа; ответом будет целое — 2.

Как целое число превратить в неправильную дробь?

Бывают ситуации, когда необходимо и такое действие. Чтобы получить неправильные дроби с заранее известным знаменателем, потребуется выполнить такой алгоритм:

Самый простой вариант, когда знаменатель равен единице. Тогда ничего умножать не нужно. Достаточно просто написать целое число, которое дано в примере, а под чертой расположить единицу.

Пример : 5 сделать неправильной дробью со знаменателем 3. После умножения 5 на 3 получается 15. Это число будет знаменателем. Ответ задания дробь: 15/3.

Два подхода к решению заданий с разными числами

В примере требуется вычислить сумму и разность, а также произведение и частное двух чисел: 2 целых 3/5 и 14/11.

В первом подходе смешанное число будет представлено в виде неправильной дроби.

После выполнения действий, описанных выше, получится такое значение: 13/5.

Для того чтобы узнать сумму, нужно привести дроби к одинаковому знаменателю. 13/5 после умножения на 11 станет 143/55. А 14/11 после умножения на 5 примет вид: 70/55. Для вычисления суммы нужно только сложить числители: 143 и 70, а потом записать ответ с одним знаменателем. 213/55 — эта неправильная дробь ответ задачи.

При нахождении разности эти же числа вычитаются: 143 — 70 = 73. Ответом будет дробь: 73/55.

При умножении 13/5 и 14/11 не нужно приводить к общему знаменателю. Достаточно перемножить попарно числители и знаменатели. Получится ответ: 182/55.

Так же и при делении. Для правильного решения нужно заменить деление на умножение и перевернуть делитель: 13/5: 14/11 = 13/5 х 11/14 = 143/70.

Во втором подходе неправильная дробь обращается в смешанное число.

После выполнения действий алгоритма 14/11 обратится в смешанное число с целой частью 1 и дробной 3/11.

Во время вычисления суммы нужно сложить целые и дробные части по отдельности. 2 + 1 = 3, 3/5 + 3/11 = 33/55 + 15/55 = 48/55. Итоговый ответ получается 3 целых 48/55. В первом подходе была дробь 213/55. Проверить правильность можно, переведя его в смешанное число. После деления 213 на 55 получается частное 3 и остаток 48. Нетрудно заметить, что ответ правильный.

При вычитании знак «+» заменяется на «-». 2 — 1 = 1, 33/55 — 15/55 = 18/55. Для проверки ответ из предыдущего подхода нужно перевести в смешанное число: 73 делится на 55 и получается частное 1 и остаток 18.

Для нахождения произведения и частного пользоваться смешанными числами неудобно. Здесь всегда рекомендуется переходить к неправильным дробям.

Как сделать из неправильной дроби правильную?

Само слово — дробь означает, что число дробное, оно меньше целого (как минимум единицы).

Следовательно, необходимо выделить целое число из числителя. Например, число 30/4 — дробь неправильная, поскольку 30 больше, чем 4. Значит, нужно просто разделить 30 на 4 и получим число до запятой — 7, его то и ставим перед дробью. Умножим 7 на 4 и вычтем это число из 30 — получится 2 — оно будет в числителе дроби. Итог — 7 2/4, сокращаем — 7 1/2. В вашем примере, ответ — 2 3/4.

Для того необходимо чтслитель: на знаменатель.

То целое, что получилось — пишите в числитель. Знаменатель тот, что был. Когда поделите — записывайте в целую часть.

Получаем правил-ую дробь: 2 — целых 34

Чтобы сделать из неправильной дроби правильную, нужно выявить целые части и отнять их из неправильной дроби. В нашем случае неправильная дробь 11/4. Целых частей будет две (2). Вычитаем их и получаем правильную дробь: две целых три четвртых (2 целых 3/4).

Неправильную дробь, в нашем случае 11/4 нужно перевести в правильную, т.е. в этом случае смешанную дробь. Если по-простому, то дробь неправильная, потому что в ней помимо дроби есть и целое число. Это как стоит в холодильнике тортик непочатый, хоть и порезанный, а на столе — осталось несколько кусочков от второго. Когда говорим об 11/4, то мы уже не знаем о двух целых тортах, видим лишь одиннадцать крупных кусков. 11 разделили на 4, получили 2, а остаток 11-8=3. Итак, 2 целых 3/4, теперь дробь правильная, в ней числитель поменьше знаменателя будет, но смешанная, так как без целых единиц расчет не обошелся.

Чтобы из неправильной дроби сделать правильную, надо числитель разделить на знаменатель. Полученное целое число выносим перед дробью, а остаток вписываем в числитель. Знаменатель не изменяется.

Например: дробь 11/4 — неправильная, где числитель равен 11, а знаменатель — 4.

Сначала 11 делим на 4, получим 2 целых и 3 остаток. Выносим 2 перед дробью, а остаток 3 пишем в числитель 3/4. Таким образом дробь становится правильной — 2 целых и 3/4.

У неправильной дроби знаменатель оказывается меньше числителя, что говорит о том, что в этой дроби имеются целые части, которые можно выделить и получить правильную дробь с целым числом.

Самый простой способ поделить числитель на знаменатель. Полученное целое число ставим слева от дроби, а остаток пишем в числитель, знаменатель остается тем же самым.

Чтобы ответить на этот несложный вопрос, можно решить такую же несложную задачку:

Петя и Валя пришли в компанию сверстников. Всех вместе их стало 11. У Вали были с собой яблоки (но не много) и чтобы угостить всех Петя разрезал каждое на четыре части и раздал. Хватило всем и даже пять кусочков осталось.

Сколько яблок раздал Петя и сколько яблок осталось? Сколько их было всего?

А можно записать это математически

11 кусочков яблока это в нашем случае 11/4 — получили неправильную дробь, так как числитель больше знаменателя.

В результате получим 11/4 = 11:4 = 2 3/4 яблока раздал Петя.

Аналогично 5/4 = 1 1/4 яблок осталось.

(11+5)/4 = 16/4 = 4 яблока принесла Валя

Преобразование дроби в десятичное число

Это обратное предыдущему преобразованию. Десятичная дробь чем характерна? У неё в знаменателе всегда стоит 10, или 100, или 1000, или 10000 и так далее. Если ваша обычная дробь имеет такой знаменатель, проблем нет. Например, или

Некоторые дроби проще разделить, чем преобразовать знаменатель. Например,

Некоторые дроби невозможно преобразовать в десятичные числа!
Например,

Преобразование смешанной дроби в неправильную

При преобразовании смешанной дроби в неправильную, можно вспомнить, что Можно использовать сложение дробей

Преобразование неправильной дроби в смешанную (выделение целой части)

Каждый человек при решении задач с математики нередко сталкивался с задачами на дроби. Их очень много, поэтому мы рассмотрим разные варианты решения основных таких задач.

Что такое дроби

Ежели знаменатель дроби (натуральное число) больше числителя дроби (натуральное число), то дробь называется правильной. Приведем примеры: 7/19; 9/13; 31/152; 5/17.

Если знаменатель дроби (натуральное число) меньше или равен числителю дроби (натуральное число), то дробь называется неправильной. Приведем примеры: 7/5; 19/3; 15/9; 231/63.

Как перевести неправильную дробь

Чтобы смешанную дробь перевести в неправильную, необходимо целую часть дроби умножить на знаменатель в дробной части и добавить числитель к этому произведению. Потом сумму взять как числитель, написав тот же, что и прежде знаменатель. Приведем примеры:

Для перевода неправильной дроби в правильную, необходимо числитель этой неправильной дроби разделить на ее знаменатель. Полученное, при этом, целое число взять целой частью дроби, ну а остаток (конечно, если он есть) взять как числитель дробной части правильной дроби, написав тот же, что и прежде знаменатель. Приведем примеры:

Для перевода неправильной дроби в десятичную необходимо выяснить, существует ли такой множитель, что позволит привести знаменатель дробной части неправильной дроби к числу, которое равно десятке (или десятке, которая возведена в любую степень (10, 100, 1000 и дальше). Если такой множитель есть, то необходимо умножить числитель и знаменатель неправильной дроби на этот множитель, чтобы проверить его. Теперь умноженный числитель необходимо приписать через запятую к целой части неправильной дроби. Приведем примеры:

Если такого множителя не существует, это означает, что эта неправильная дробь в десятичной форме не имеет четкого эквивалента. То есть, не каждую неправильную дробь можно перевести в десятичную. В этом случае, Вам необходимо найти приблизительное значение дроби с необходимой для Вас степенью точности. Посчитать такую дробь можно на калькуляторе, в уме или в столбик. Приведем примеры: 41/7 = 5(6/7) = 5,9 (с округлением до десятых), = 5,86 (с округлением до сотых), = 5,857 (с округлением до тысячных); 3/7, 7/6, 1/3 и другие. Также четко не переводятся и считаются на калькуляторе, в уме или в столбик.

Теперь Вы знаете, как перевести неправильную дробь в правильную или десятичную дробь!

Нехитрые математические правила и приемы, если они не используются постоянно, забываются быстрее всего. Еще быстрее уходят из памяти термины.

Одно из таких простых действий – преобразование неправильной дроби в правильную или, по-другому – смешанную.

Неправильная дробь

Неправильной называется дробь, у которой числитель (число над дробной чертой) больше или равно знаменателю (число под чертой). Такая дробь получается при сложении дробей или умножении дроби на целое число. По правилам математики такую дробь обязательно нужно превратить в правильную.

Правильная дробь

Логично предположить, что правильными называются все остальные дроби. Строгое определение – правильной называется дробь, у которой числитель меньше знаменателя. Дробь, у которой есть целая часть иногда называется смешанной.

Преобразование неправильной дроби в правильную

Но прежде чем приводить дробь к правильному виду, нужно проверить, можно ли её сократить.
Сокращение дроби возможно, если у числителя и знаменателя есть общий делитель. То есть такое число, на которое и то, и другое делится без остатка. Если таких делителей несколько, нужно найти наибольший.
Например, у всех четных чисел такой общий делитель – двойка. А у дроби шестнадцатых двенадцатых, есть еще один общий делитель – четверка. Это наибольший делитель. Разделите числитель и знаменатель на четыре. Результат сокращения: четыре третьих. А теперь, в качестве тренировки, преобразуйте эту дробь в правильную.

В этом материале мы разберем такое понятие, как смешанные числа. Начнем, как всегда, с определения и небольших примеров, потом поясним связь смешанных чисел и неправильных дробей. После этого мы изучим, как правильно выделять целую часть из дроби и получать в результате целое число.

Понятие смешанного числа

Числа вида 0 3 14 также не относятся к смешанным. Здесь не выполняется первая часть условия: целая часть должна быть представлена только натуральным числом, а нуль им не является.

Как соотносятся между собой неправильные дроби и смешанные числа

Эту связь проще всего проследить на конкретном примере.

Наш пример доказывает, что в виде смешанного числа можно представить любую неправильную дробь.

Мы поняли, как приводить неправильную дробь к виду смешанного числа. Если в числителе неправильной дроби стоит такое число, которое можно разделить на знаменатель без остатка, то можно сделать это, и тогда наша неправильная дробь станет натуральным числом.

Как перевести смешанное число в неправильную дробь

Чтобы успешно решать задачи, полезно уметь производить и обратное действие, то есть делать из смешанных чисел неправильные дроби. В этом пункте мы разберем, как правильно это сделать.

Для этого нужно воспроизвести следующую последовательность действий:

1. Для начала представляем имеющееся смешанное число n a b как сумму целой и дробной части. Получается n + a b

Разберем это действие на конкретном примере.

Представьте 5 3 7 в виде неправильной дроби.

Последний шаг – сложение дробей, имеющих разные знаменатели:

5 1 + 3 7 = 35 7 + 3 7 = 38 7

Представьте 15 2 5 в виде неправильной дроби.

Обычно мы не указываем неправильную дробь в качестве итогового ответа. Принято доводить вычисления до конца и заменять ее либо натуральным числом (разделив числитель на знаменатель), либо смешанным числом. Как правило, первый способ используется, когда разделить числитель на знаменатель можно без остатка, а второй – если такое действие невозможно.

Когда мы выделяем из неправильной дроби целую часть, мы просто заменяем ее равным смешанным числом.

Разберем, как именно это делается.

Приведем доказательство этого утверждения.

Выделение целой части из неправильной дроби a b осуществляется таким образом:

1) производим деление a на b с остатком и записываем неполное частное q и остаток r отдельно.

Представьте 107 4 в виде смешанного числа.

Делим 104 на 7 столбиком:

Нам осталось посмотреть, как заменить неправильную дробь натуральным числом (при условии, что ее числитель делится на знаменатель без остатка).

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

Сложение и вычитание смешанных чисел

Смешанные числа: определения, примеры

Где n — целая часть, — дробная часть.

Примеры смешанных чисел

Каждое такое смешанное число содержит целую и дробную части.

Чтобы точно определять, какая именно перед вами дробь, запомните:

Дробь вида называется правильной дробью. В ней числитель всегда меньше знаменателя.

Дробь вида называется неправильной. В таких дробях числитель больше знаменателя или равен ему.

Дробь вида называется смешанной дробью/смешанным числом. Такая дробь состоит из целой части (натуральное число) и дробной части.

Смешанные числа можно складывать, вычитать, умножать и делить. Давайте узнаем, как именно это делать.

Онлайн-курсы математики для детей помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.

Сложение смешанных чисел

Всего мы рассмотрим три типа сложения со смешанными числами. В каждом подпункте приведено необходимое правило и примеры выполнения решений.

Сложение смешанного числа и натурального числа

Представим первое правило в виде буквенных выражений.

Выполним сложение смешанного числа и натурального числа d.

Известно, что любое смешанное число равное сумме целой и дробной частей.

Рассмотрим примеры сложения смешанных чисел с натуральными числами.

Пример 1. Выполните сложение смешанного числа и натурального числа 18.

Пример 2. Выполните сложение смешанного числа и натурального числа 10.

Пример 3. Выполните сложение смешанного числа и натурального числа 2.

Сложение смешанного числа со смешанным числом

Представим правило в виде буквенных выражений.

Рассмотрим примеры сложения смешанных чисел.

Согласно правилу, складываем последовательно целые части смешанных чисел, затем складываем дробные части:

Решаем: складываем целые части 2 + 7 = 9.

Чтобы выполнить сложение дробных частей, воспользуемся правилом сложения дробей с разными знаменателями: приведем дроби к наименьшему общему знаменателю и выполним сложение.

Наименьшее общее кратное — 15.

Решаем: складываем целые части 13 + 2 = 15.

Складываем дробные части

Наименьшее общее кратное 12 и 20 равно 60.

Таким же образом можно складывать три, четыре и больше натуральных чисел. Не забывайте сокращать дроби и выделять целые части из неправильных дробей.

Сложение смешанного числа и правильной дроби

Представим правило в виде буквенного выражения.

Рассмотрим примеры сложения смешанных чисел с обыкновенными дробями.

Пример 1. Выполните сложение обыкновенной дроби и смешанного числа

Согласно правилу, складываем дробь с дробной частью смешанного числа:

Наименьшее общее кратное 5 и 20 равно 20.

Следуя правилу, складываем дробь с дробной частью смешанного числа:

Наименьшее общее кратное 4 и 2 равно 4.

Чтобы выполнить сложение смешанного числа и неправильной обыкновенной дроби, выделите целую часть из неправильной дроби и выполните сложение смешанных чисел.

Вычитание смешанных чисел

Рассмотрим три типа вычитания со смешанными числами. В каждом подпункте вы найдете правила и решение примеров с разбором.

Вычитание одного смешанного числа из другого

Исходя из значения дробных частей, вычитание можно выполнять тремя способами.

Чтобы решить пример, нужно выяснить, какая из дробных частей больше:

Чтобы сравнить две дроби, приведем их к общему знаменателю — 8:

По правилу сравнения дробей с одинаковыми знаменателями, больше та дробь, чей числитель больше.

Пример. Выполните вычитание:

Следуя правилу, выполним вычитание:

Пример. Найдите значение разности смешанных чисел и

Сначала выясним, как из дробных частей больше. Для этого приведем их к НОЗ.

Следуя правилу, решаем:

Представим число 21 в виде смешанной дроби и выполним вычитание дроби из натурального числа:

Вычитание смешанного числа из натурального числа

Пример. Отнимите от натурального числа 15 смешанное число

Следуя правилу, выполним вычитание целой части смешанного числа из натурального числа:

Умножение смешанных чисел

Давайте разберемся как выполнять умножение в примерах, где есть смешанные числа.

Умножение смешанного числа на смешанное число

Пример. Выполните умножение смешанного числа и

Следуя правилу, переведем смешанные числа в неправильные дроби.

Умножение смешанного числа на обыкновенную дробь

Пример. Умножьте смешанное число на обыкновенную дробь

Представим смешанное число в виде неправильной дроби.

Выполним умножение дробей

Выделим из полученной неправильной дроби целую часть

Умножение целого числа на дробь

Пример. Выполните умножение числа 7 на обыкновенную дробь

Деление смешанных чисел

Вы уже рассмотрели три типа арифметических действий со смешанными числами. Осталось разобраться, как выполнять деление в примерах, где есть смешанные числа. Давай научимся это делать.

Деление смешанного числа на смешанное число

Пример. Найдите результат деления смешанного числа на смешанное число

Следуя правилу, переведем оба смешанных числа в неправильные дроби.

Пользуясь правилом деления дробей, находим частное:

Деление смешанного числа на целое число

Пример. Разделите смешанное число на натуральное число 15

Следуя правилу, переведем смешанное число в неправильную дробь

Деление целого числа на смешанное число

Пример. Выполните деление натурального числа 30 на смешанное число

Деление смешанного числа на обыкновенную дробь

Пример. Разделите смешанное число на обыкновенную дробь

Как из неправильной дроби получить смешанное число. Как сделать из неправильной дроби правильную

Для того необходимо чтслитель: на знаменатель.

Чтобы сделать из неправильной дроби правильную, нужно выявить целые части и отнять их из неправильной дроби. В нашем случае неправильная дробь 11/4. Целых частей будет две (2). Вычитаем их и получаем правильную дробь: две целых три четвртых (2 целых 3/4).

Чтобы из неправильной дроби сделать правильную, надо числитель разделить на знаменатель. Полученное целое число выносим перед дробью, а остаток вписываем в числитель. Знаменатель не изменяется.

У неправильной дроби знаменатель оказывается меньше числителя, что говорит о том, что в этой дроби имеются целые части, которые можно выделить и получить правильную дробь с целым числом.

Самый простой способ поделить числитель на знаменатель. Полученное целое число ставим слева от дроби, а остаток пишем в числитель, знаменатель остается тем же самым.

Чтобы ответить на этот несложный вопрос, можно решить такую же несложную задачку:

Петя и Валя пришли в компанию сверстников. Всех вместе их стало 11. У Вали были с собой яблоки (но не много) и чтобы угостить всех Петя разрезал каждое на четыре части и раздал. Хватило всем и даже пять кусочков осталось.

Сколько яблок раздал Петя и сколько яблок осталось? Сколько их было всего?

А можно записать это математически

В результате получим 11/4 = 11:4 = 2 3/4 яблока раздал Петя.

Аналогично 5/4 = 1 1/4 яблок осталось.

(11+5)/4 = 16/4 = 4 яблока принесла Валя

Навигация по странице.

Смешанные числа, определение, примеры

Так мы подошли к определению смешанного числа.

Связь между смешанными числами и неправильными дробями

Проследить связь между смешанными числами и неправильными дробями лучше всего на примерах.

Перевод смешанного числа в неправильную дробь

Для выполнения различных действий со смешанными числами оказывается полезным навык представления смешанных чисел в виде неправильных дробей. В предыдущем пункте мы выяснили, что любое смешанное число можно перевести в неправильную дробь. Пришло время разобраться, как осуществляется такой перевод.

Запишем алгоритм, показывающий как перевести смешанное число в неправильную дробь :

Рассмотрим пример перевода смешанного числа в неправильную дробь.

Представьте смешанное число в виде неправильной дроби.

Выполним все необходимые шаги алгоритма.

Чтобы закончить перевод исходного смешанного числа в неправильную дробь, осталось выполнить сложение дробей с разными знаменателями : .

Краткая запись всего решения такова: .

Запишите смешанное число в виде неправильной дроби.

Выделение целой части из неправильной дроби

В ответе не принято записывать неправильную дробь. Неправильную дробь предварительно заменяют либо равным ей натуральным числом (когда числитель делится нацело на знаменатель), либо проводят так называемое выделение целой части из неправильной дроби (когда числитель не делится нацело на знаменатель).

Выделение целой части из неправильной дроби – это замена дроби равным ей смешанным числом.

Осталось узнать, как можно выделить целую часть из неправильной дроби.

Докажем это утверждение.

Дробь представляет собой число, которое состоит из одной или нескольких долей единицы. В математике существует три вида дробей: обыкновенные, смешанные и десятичные.

Обыкновенная дробь записывается как соотношение, в котором в числителе отражается, сколько взято частей от числа, а знаменатель показывает, на сколько частей разделена единица. Если числитель меньше знаменателя, то перед нами правильная дробь.Например: ½, 3/5, 8/9.

В общем виде смешанная дробь может быть представлена формулой:

Таким образом, смешанная дробь записывается как целое число и обыкновенная правильная дробь, а под такой записью понимают сумму целого и его дробной части.

Десятичная дробь – это особая разновидность дроби, у которой знаменатель может быть представлен как степень числа 10. Существуют бесконечные и конечные десятичные дроби. При записи этой разновидности дроби сначала указывается целая часть, затем через разделитель (точку или запятую) фиксируется дробная часть.

Запись дробной части всегда определяется ее размерностью. Десятичная запись выглядит следующим образом:

Правила перевода между различными видами дробей

Смешанную дробь можно перевести только в неправильную. Для перевода необходимо целую часть привести и тому же знаменателю, что и дробную. В общем виде это будет выглядеть следующим образом:
Рассмотрим использование этого правила на конкретных примерах:

Неправильную обыкновенную дробь можно превратить в смешанную путем простого деления, в результате которого находится целая часть и остаток (дробная часть).

Для примера переведем дробь 439/31 в смешанную:
​​

В некоторых случаях перевести дробь в десятичную достаточно просто. В этом случае применяется основное свойство дроби, числитель и знаменатель умножаются на одно и то же числу, для того, чтобы привести делитель к степени числа 10.

В некоторых случаях может понадобиться найти частное путем деления уголком или с помощью калькулятора. А некоторые дроби невозможно привести к конечной десятичной дроби. Например, дробь 1/3 при делении никогда не даст конечный результат.

Нехитрые математические правила и приемы, если они не используются постоянно, забываются быстрее всего. Еще быстрее уходят из памяти термины.

Одно из таких простых действий – преобразование неправильной дроби в правильную или, по-другому – смешанную.

Неправильная дробь

Неправильной называется дробь, у которой числитель (число над дробной чертой) больше или равно знаменателю (число под чертой). Такая дробь получается при сложении дробей или умножении дроби на целое число. По правилам математики такую дробь обязательно нужно превратить в правильную.

Правильная дробь

Логично предположить, что правильными называются все остальные дроби. Строгое определение – правильной называется дробь, у которой числитель меньше знаменателя. Дробь, у которой есть целая часть иногда называется смешанной.

Преобразование неправильной дроби в правильную

Но прежде чем приводить дробь к правильному виду, нужно проверить, можно ли её сократить.
Сокращение дроби возможно, если у числителя и знаменателя есть общий делитель. То есть такое число, на которое и то, и другое делится без остатка. Если таких делителей несколько, нужно найти наибольший.
Например, у всех четных чисел такой общий делитель – двойка. А у дроби шестнадцатых двенадцатых, есть еще один общий делитель – четверка. Это наибольший делитель. Разделите числитель и знаменатель на четыре. Результат сокращения: четыре третьих. А теперь, в качестве тренировки, преобразуйте эту дробь в правильную.

Каждый человек при решении задач с математики нередко сталкивался с задачами на дроби. Их очень много, поэтому мы рассмотрим разные варианты решения основных таких задач.

Что такое дроби

Ежели знаменатель дроби (натуральное число) больше числителя дроби (натуральное число), то дробь называется правильной. Приведем примеры: 7/19; 9/13; 31/152; 5/17.

Если знаменатель дроби (натуральное число) меньше или равен числителю дроби (натуральное число), то дробь называется неправильной. Приведем примеры: 7/5; 19/3; 15/9; 231/63.

Как перевести неправильную дробь

Чтобы смешанную дробь перевести в неправильную, необходимо целую часть дроби умножить на знаменатель в дробной части и добавить числитель к этому произведению. Потом сумму взять как числитель, написав тот же, что и прежде знаменатель. Приведем примеры:

Для перевода неправильной дроби в правильную, необходимо числитель этой неправильной дроби разделить на ее знаменатель. Полученное, при этом, целое число взять целой частью дроби, ну а остаток (конечно, если он есть) взять как числитель дробной части правильной дроби, написав тот же, что и прежде знаменатель. Приведем примеры:

Для перевода неправильной дроби в десятичную необходимо выяснить, существует ли такой множитель, что позволит привести знаменатель дробной части неправильной дроби к числу, которое равно десятке (или десятке, которая возведена в любую степень (10, 100, 1000 и дальше). Если такой множитель есть, то необходимо умножить числитель и знаменатель неправильной дроби на этот множитель, чтобы проверить его. Теперь умноженный числитель необходимо приписать через запятую к целой части неправильной дроби. Приведем примеры:

Если такого множителя не существует, это означает, что эта неправильная дробь в десятичной форме не имеет четкого эквивалента. То есть, не каждую неправильную дробь можно перевести в десятичную. В этом случае, Вам необходимо найти приблизительное значение дроби с необходимой для Вас степенью точности. Посчитать такую дробь можно на калькуляторе, в уме или в столбик. Приведем примеры: 41/7 = 5(6/7) = 5,9 (с округлением до десятых), = 5,86 (с округлением до сотых), = 5,857 (с округлением до тысячных); 3/7, 7/6, 1/3 и другие. Также четко не переводятся и считаются на калькуляторе, в уме или в столбик.

Теперь Вы знаете, как перевести неправильную дробь в правильную или десятичную дробь!