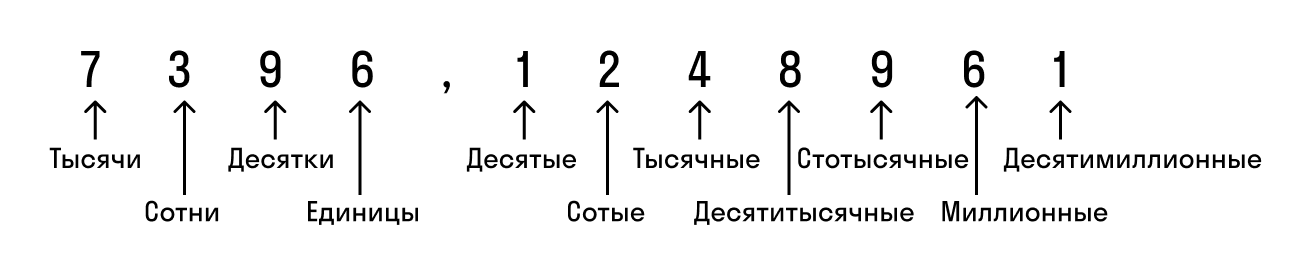
Как из неправильной дроби сделать десятичную
Как из неправильной дроби сделать десятичную
Как перевести дробь в десятичную и наоборот
Что такое дробь: понятие
Дробь — это запись числа в математика, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которой можно представить число. Есть два формата записи:
В обыкновенной дроби над чертой принято писать делимое, которое становится числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление.
Дроби бывают двух видов:
Дробь называют правильной, когда ее числитель меньше знаменателя. Например, 3/7 и 31/45.
Неправильной — ту, у которой числитель больше знаменателя или равен ему. Например, 21/4. Такое число является смешанным и читается, как «пять целых одна четвертая», а записывается — 5 1\4.
Что такое десятичная дробь
Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.
В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. По сути, десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:
Конечная десятичная дробь — это дробь, в которой количество цифр после запятой точно определено.
Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.
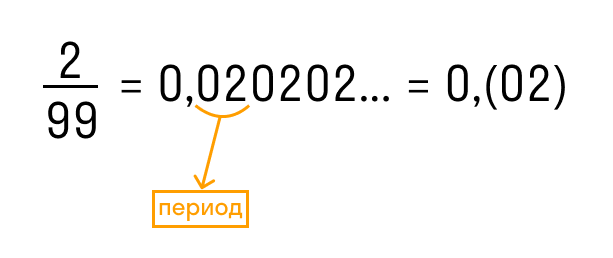
В краткой записи периодической дроби повторяющиеся цифры пишут в скобках и называют периодом дроби. Например, вместо 1,555… записывают 1,(5) и читают «одна целая и пять в периоде».
Обучение на курсах математики в Skysmart поможет улучшить оценки в школе и подготовиться к выпускным экзаменам!
Свойства десятичных дробей
Главное свойство десятичной дроби звучит так: если к десятичной дроби справа приписать один или несколько нулей — ее величина не изменится. Это значит, что если в вашей дроби куча нулей — их можно просто отбросить. Например:
Обыкновенная и десятичная дробь — давние друзья. Вот как они связаны:
Как перевести обычную дробь в десятичную
Прежде чем узнать, как от обычной записи перейти к десятичной, вспомним различия двух видов дробей и сформулируем важное правило.
Обыкновенную дробь можно перевести в конечную десятичную дробь только при условии, что её знаменатель можно разложить на простые множители 2 и 5 любое количество раз. Например:
Дробь 11/40 можно преобразовать в конечную десятичную, потому что знаменатель раскладывается на множители 2 и 5.
Дробь 17/60 нельзя преобразовать в конечную десятичную дробь, потому что в её знаменателе кроме множителей 2 и 5, есть 3.
А теперь перейдем к самому главному вопросу: рассмотрим несколько алгоритмов перевода обыкновенной дроби в десятичную.
Способ 1. Превращаем знаменатель в 10, 100 или 1000
Чтобы превратить дробь в десятичную, нужно числитель и знаменатель умножить на одно и то же число так, чтобы в знаменателе получилось 10, 100, 1000 и т.д. Но прежде, чем приступать к вычислениям, нужно проверить, можно ли вообще превратить данную дробь в десятичную.
Для примера возьмем дробь 3/20. Ее можно привести в конечную десятичную, потому что её знаменатель раскладывается на множители 2 и 5.
Мы можем получить в нижней части 100: достаточно умножить 20 на 5. Про верхнюю часть тоже не забываем: получаем 15.
Теперь запишем числитель отдельно. Отсчитываем справа столько же знаков, сколько нулей стоит в знаменателе, и ставим запятую. В нашем примере в знаменателе 100 (у него два нуля), значит ставим запятую после отсчета двух знаков и получаем 0,15. Преобразование готово.
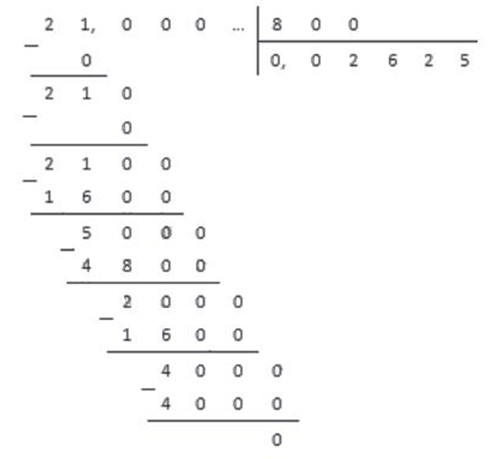
Способ 2. Делим числитель на знаменатель
Чтобы перевести обыкновенную дробь в десятичную, достаточно разделить ее верхнюю часть на нижнюю. Проще всего это сделать, конечно же, на калькуляторе — но на контрольных им пользоваться не разрешают, поэтому учимся по-другому.
Для примера возьмем дробь 78/100. Убедимся, что дробь можно привести в конечную десятичную.
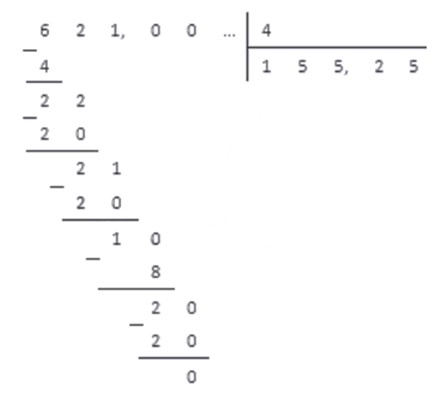
Делим столбиком числитель на знаменатель — преобразование готово:
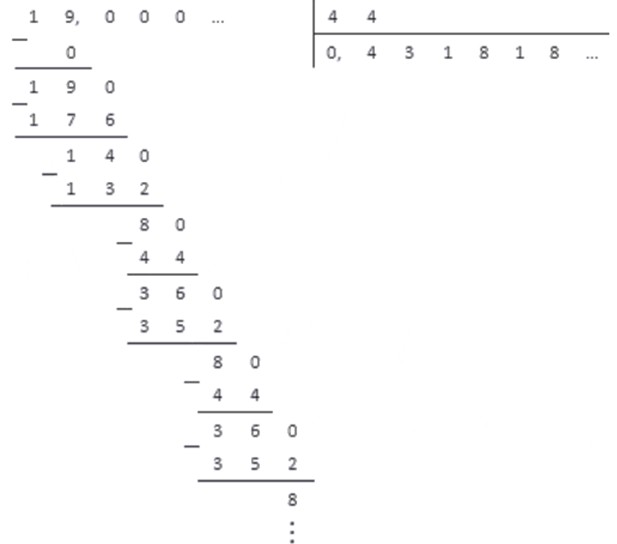
Если при делении уголком стало ясно, что процесс не заканчивается и после запятой выстраиваются повторяющиеся цифры — эту дробь нельзя перевести в конечную десятичную. Ответ можно записать в виде периодической дроби — для этого нужно записать повторяющееся число в скобки, вот так: 1/3 = 0,3333.. = 0,(3).
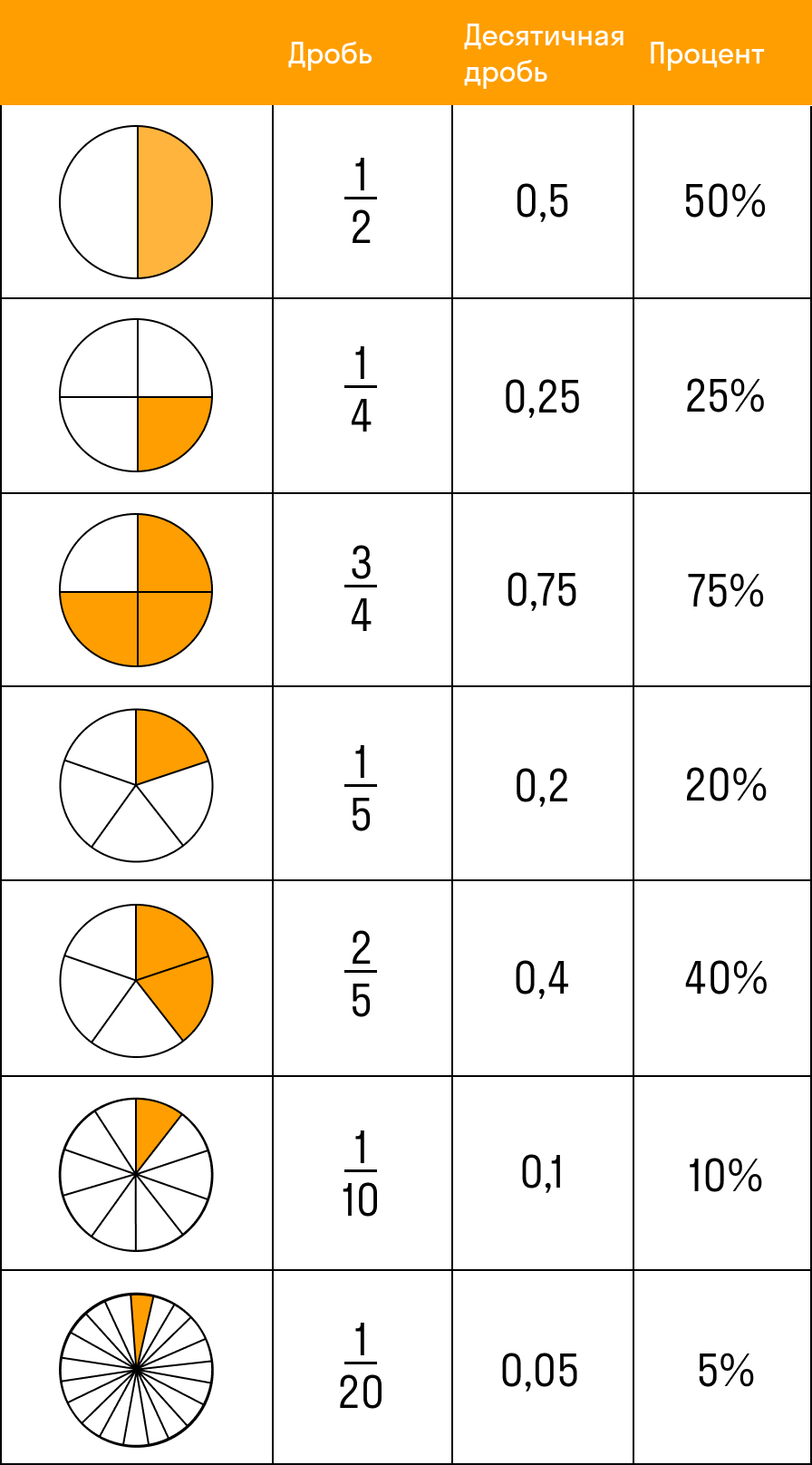
Для удобства мы собрали табличку дробей со знаменателями, которые чаще всего встречаются в заданиях по математике. Скачайте ее на гаджет или распечатайте и храните в учебнике как закладку:
Как перевести десятичную дробь в обыкновенную
Не будем придумывать велосипед. По сути, алгоритм превращения десятичной дроби в обыкновенную противоположен тем, что мы разобрали в предыдущей части. Вот, как это выглядит в обратную сторону:
Не забывайте про минус в ответе, если пример был про отрицательное число. Очень обидная ошибка!
| Еще алгоритм: как преобразовать десятичную дробь в обыкновенную Вот и всё! Эта схема значительно проще и быстрее. Проверим: Как видим, в дроби 0,55 после запятой стоит две цифры — 5 и 5. Поэтому n = 2. Если убрать запятую и нули слева, то получим число 55. Переходим ко второму шагу: 10n = 102 = 100, поэтому в знаменателе стоит 100. Остается сократить числитель и знаменатель. Вот и ответ: 11/20. Перевод десятичной дроби в обыкновенную и наоборот: правило, примерыБывает, что для удобства расчетов нужно перевести обыкновенную дробь в десятичную и наоборот. О том, как это делать, мы поговорим в данной статье. Разберем правила перевода обыкновенных дробей в десятичные и обратно, а также приведем примеры. Перевод обыкновенных дробей в десятичныеМы будем рассматривать перевод обыкновенных дробей в десятичные, придерживаясь определенной последовательности. Во первых, рассмотрим, как в десятичные переводятся обыкновенные дроби со знаменателем, кратным 10: 10, 100, 1000 и т.д.Дроби с такими знаменателями, по сути, являются, более громоздкой записью десятичных дробей. Далее мы рассмотрим, как переводить в десятичные дроби обыкновенные дроби с любым, не только кратным 10, знаменателем. Отметим, что при обращении обыкновенных дробей в десятичные получаются не только конечные десятичные, но и бесконечные периодические десятичные дроби. Перевод обыкновенных дробей со знаменателями 10, 100, 1000 и т.д. в десятичные дробиПервым делом, скажем, что некоторые дроби нуждаются в определенной подготовке перед обращением в десятичный вид. В чем она заключается? Перед цифрой, стоящей в числителе, необходимо дописать столько нулей, чтобы количество цифр числителя стало равно числу нулей в знаменателе. Например, для дроби 3100 число 0 необходимо один раз дописать слева от 3 в числителе. Дробь 610, согласно изложенному выше правилу, не нуждается в доработке. Рассмотрим еще один пример, после чего сформулируем правило, которым особенно удобно пользоваться на первых порах, пока опыта в обращении дробей не так много. Так, дробь 1610000 после дописывания нулей в числителе будет иметь вид 001510000. Как перевести обыкновенную дробь со знаменателем 10, 100, 1000 и т.д. в десятичную? Правило перевода обыкновенных правильных дробей в десятичные Теперь перейдем к примерам. Пример 1. Перевод обыкновенных дробей в десятичные Переведем обыкновенную дробь 39 100 в десятичную. Разберем решение еще одного примера по этой теме. Пример 2. Перевод обыкновенных дробей в десятичные Запишем дробь 105 10000000 в виде десятичной дроби. Правило перевода обыкновенных неправильных дробей в десятичные Ниже приведем пример на использование этого правила. Пример 3. Перевод обыкновенных дробей в десятичные Переведем дробь 56888038009 100000 из обыкновенной неправильной в десятичную. Сначала запишем число из числителя: Следующий вопрос, который закономерно возникает: как перевести в десятичную дробь смешанное число, если знаменателем его дробной части является число 10, 100, 1000 и т.д. Для обращения в десятичную дробь такого числа можно воспользоваться следующим правилом. Правило перевода смешанных чисел в десятичные дроби Обратимся к примеру. Пример 4. Перевод смешанных чисел в десятичные дроби Переведем смешанное число 23 17 10000 в десятичную дробь. После запятой записываем число из числителя вместе с нулями. Получаем результат: Перевод обыкновенных дробей в конечные и бесконечные периодические дробиКонечно, можно переводить в десятичные дроби и обыкновенные дроби со знаменателем, не равным 10, 100, 1000 и т.д. Часто дробь можно легко привести к новому знаменателю, а затем уже воспользоваться правилом, изложенным в первом пункте данной статьи. Например, достаточно умножить числитель и знаменатель дроби 25 на 2, и мы получим дробь 410, которая легко приводится к десятичному виду 0,4. Однако такой способ перевода обыкновенной дроби в десятичную удается использовать не всегда. Ниже рассмотрим, как поступать, если применить рассмотренный способ невозможно. Принципиально новый способ обращения обыкновенной дроби в десятичную сводится к делению числителя на знаменатель столбиком. Эта операция очень похожа на деление натуральных чисел столбиком, но имеет свои особенности. Пример 5. Перевод обыкновенных дробей в десятичные Переведем обыкновенную дробь 621 4 в десятичный вид. Когда мы добрались до десятичной запятой в делимом, а остаток отличен от нуля, ставим в частном десятичную запятую, и продолжаем делить, не обращая более внимания на запятую в делимом. Рассмотрим решение еще одного примера, чтобы закрепить материал. Пример 6. Перевод обыкновенных дробей в десятичные Но как быть, если при делении мы так и не получим в остатке 0. В таких случаях деление можно продолжать бесконечно долго. Однако, начиная с определенного шага, остатки будут периодически повторяться. Соответственно, будут повторяться и цифры в частном. Это значит, что обыкновенная дробь переводится в десятичную бесконечную периодическую дробь. Проиллюстрируем сказанное на примере. Пример 7. Перевод обыкновенных дробей в десятичные Обратим обыкновенную дробь 19 44 в десятичную. Для этого выполним деление столбиком. Таким образом, исходная обыкновенная дробь переведена в бесконечную периодическую десятичную дробь. Во первых, скажем, что если дробь удается привести к одному из знаменателей 10, 100, 1000. то она будет иметь вид конечной десятичной дроби. Чтобы дробь приводилась к одному из таких знаменателей, ее знаменатель должен быть делителем хотя бы одного из чисел 10, 100, 1000 и т.д. Из правил разложения чисел на простые множители следует, что делитель чисел 10, 100, 1000 и т.д. должен, при разложении на простые множители, содержать лишь числа 2 и 5. Пример 8. Перевод обыкновенных дробей в десятичные Обыкновенную дробь нельзя перевести в бесконечную и непериодическую десятичную дробьВыше мы говорили только о конечных и бесконечных периодических дробях. Но может ли какая-либо обыкновенная дробь быть обращена в вид бесконечной непериодической дроби? При переводе бесконечной дроби в десятичную получается либо конечная десятичная дробь, либо бесконечная периодическая десятичная дробь. Остаток от деления всегда меньше делителя. Другими словами, согласно теореме о делимости, если мы делим какое-то натуральное число на число q, то остаток деления в любом случае не может быть больше, чем q-1. После окончания деления возможна одна из следующих ситуаций: Иных вариантов при обращении обыкновенной дроби в десятичную не может быть. Скажем также, что длина периода (количество цифр) в бесконечной периодической дроби всегда меньше, чем число цифр в знаменателе соответствующей обыкновенной дроби. Перевод десятичных дробей в обыкновенные дробиТеперь пришло время рассмотреть обратный процесс перевода десятичной дроби в обыкновенную. Сформулируем правило перевода, которое включает три этапа. Как перевести десятичную дробь в обыкновенную? Правило перевода десятичных дробей в обыкновенные дроби Рассмотрим применение данного правила на примерах. Пример 8. Перевод десятичных дробей в обыкновенные Если в десятичной дроби есть целая часть, то такую дробь можно сразу перевести в смешанное число. Как это сделать? Сформулируем еще одно правило. Правило перевода десятичных дробей в смешанные числа. Обратимся к примеру Пример 10. Перевод десятичной дроби в смешанное число Поучаем смешанное число: 155 6005 100000 Перевод бесконечных периодических десятичных дробей в обыкновенные дробиРазберем на примерах, как осуществлять перевод периодических десятичных дробей в обыкновенные. Прежде чем начать, уточним: любую периодическую десятичную дробь можно перевести в обыкновенную. Пример 11. Перевод периодической десятичной дроби в обыкновенную Обращая данную дробь в обыкновенную по алгоритму, разобранному в предыдущих пунктах, получаем: Как быть, если период дроби отличен от нуля? Периодическую часть следует рассматривать как сумму членов геометрический прогрессии, которая убывает. Поясним это на примере: Рассмотрим несколько примеров с применением данной формулы. Пример 12. Перевод периодической десятичной дроби в обыкновенную Это и есть искомая обыкновенная дробь. Для закрепления материала рассмотрим еще один пример. Пример 13. Перевод периодической десятичной дроби в обыкновенную Сначала записываем дробь в виде бесконечной суммы: Рассмотрим слагаемые в скобках. Эту геометрическую прогрессию можно представить в следующем виде: После сложения данных дробей и сокращения получим окончательный ответ: В завершение данной статьи скажем, что непериодические бесконечный десятичные дроби нельзя перевести в вид обыкновенных дробей. Перевод обыкновенной дроби в десятичную и наобороттеория по математике 📈 числа и вычисленияПри решении различных вычислительных заданий требуется произвести перевод десятичной дроби в обыкновенную или наоборот. В частности, в бланках ответов первой части ОГЭ (и ЕГЭ) нельзя записывать обыкновенную дробь, так как поле для этой дроби просто не существует. Чтобы перевести обыкновенную дробь в конечную десятичную дробь, необходимо разделить числитель дроби на ее знаменатель. Как перевести обыкновенную дробь в конечную десятичную дробь? Чтобы перевести обыкновенную дробь в конечную десятичную дробь, необходимо разделить числитель дроби на ее знаменатель (устно или в Пример №1. ½ = 0,5 так как 1:2=0,5 Пример №2. ¾ = 0,75 так как 3:4=0,75 Пример №3. Так как 18:25=0,72, то Если дана смешанная дробь, то целая часть уже есть, делим числитель на знаменатель и добавляем в часть после запятой. Или переводим смешанное число в неправильную дробь и делим числитель на знаменатель. Строгого правила для способа выполнения данного действия нет. Пример №4. здесь целая часть 14 уже есть, пишем ее и ставим запятую. Затем делим 3 на 50 и получаем 0,06. Приписываем десятичную часть 06 после запятой к числу 14 и получаем 14,06. Пример №5. в данном случае сначала перевели смешанное число в неправильную дробь (знаменатель умножается на целую часть и прибавляется числитель – это число записывается в числитель неправильной дроби), а затем разделили числитель 703 на знаменатель 50 и получили 14,06. Как перевести десятичную дробь (конечную) в обыкновенную? Чтобы перевести десятичную дробь в обыкновенную, нужно в числитель записать цифры из десятичной части дроби (которые стоят после запятой), а в знаменателе написать столько нулей, сколько цифр получилось в числителе. Затем, по возможности сократить данную дробь. Пример №6. целая часть равна нулю, нуль перед обыкновенной дробью не пишется, 17 записали в числитель, а 100 в знаменатель, так как в числе 17 две цифры, как у сотни два нуля. Пример №7. целая часть равна 5, поэтому записали ее перед дробью, 34 пошло в числитель, а знаменатель соответственно равен 100 (по количеству цифр в числе 34). Здесь видно, что получилась сократимая дробь, так как числитель и знаменатель оба делятся на 2. Выполняем сокращение дробной части и получаем новую дробь Сначала выразим обыкновенную дробь десятичной, разделив 107 на 13, получаем приближенное число 8,23…. Теперь работаем с числовым лучом, на котором видно, что наше число 8,23.. будет располагаться между числами 8 и 9, но ближе к 8, так как оно меньше 8,5; следовательно, это точка А. pазбирался: Даниил Романович | обсудить разбор | оценить Одно из чисел Точка, обозначенная на прямой, лежит между 2 и 3. Т.е. соответствующее ей число больше 1. Это значит, что дробь, которая соответствует этой точке, должна быть неправильной. Но все приведенные в условии дроби неправильные. Чтобы понять, какая из них находится именно на промежутке (2; 3), необходимо выделить их целые части. Та из дробей, у которой целая часть окажется равной 2, и есть искомый результат. Итак, выделяем целые части: Целую часть, равную 2, имеют две дроби – 1-я и 4-я. Но посмотрим внимательно на прямую. Обозначенная на ней точка находится близко к делению 3. Проанализируем в этом контексте подходящие нам дроби. У первой недостает всего 2/11, чтобы она стала равной 3, между тем как четвертая лишь на 2/11 удалена от деления 2. Следовательно, правильным ответом в данном случае является дробь 31/11. Она соответствует варианту ответа 2. pазбирался: Даниил Романович | обсудить разбор | оценить На координатной прямой отмечена точка А: Известно, что она соответствует одному из четырёх указанных ниже чисел. Какому из чисел соответствует точка А? Подход к решению в данной задаче сводится к визуальной оценки имеющихся вариантов на координатной прямой, для этого необходимо предварительно перевести варианты ответов к примерному десятичному виду. Оцениваем 181/16 – можно поделить 181 на 16, тогда получим 11,3125. Это явно выходит за указанный диапазон, поэтому данный вариант нам не подходит. Оцениваем √37 – самое близкое значение, из которого вычисляется квадратный Посмотрим на вариант 0,6 – это явно меньше единицы, а точка А, как мы уже выяснили, лежит в диапазоне 5-10. Данный вариант нам не подойдет. Вариант с ответом 4 также не подойдет по вышеуказанной причине. pазбирался: Даниил Романович | обсудить разбор | оценить В задании данного типа необходимо выполнить деление 8 на 3 и 11 на 4, то есть перевести дробь из обыкновенного вида в десятичный. Сами дроби могут не иметь представления в десятичном виде, однако в нашем случае достаточно выполнить деление но второго знака после запятой, так как в ответе приведены числа до первого знака после запятой. Итак, выполняем деление: Получаем значения 2,666.. или 2,(6) и 2,75. Смотрим на варианты ответов и выбираем, соответственно, первый, так как 2,7 находится между 2,(6) и 2,75. pазбирался: Даниил Романович | обсудить разбор | оценить К данному заданию, как и к большинству заданий 1 модуля Алгебры, подход к решению заключается в переводе дроби от одного вида к другому. В нашем случае это переход от обыкновенной дроби к десятичной. Переводим ¼ из обыкновенной дроби в десятичную. Делим 1 на 4, получаем 0,25. Затем переписываем выражение с использованием только десятичных дробей и вычисляем: pазбирался: Даниил Романович | обсудить разбор | оценить Задачу можно решать разными путями, а именно менять последовательность действий, но этот вариант решения рекомендуется для тех, кто уверен в своих возможностях и знает математику на отлично. Для остальных мы рекомендуем выполнить последовательно действия в числителе и знаменателе, а затем разделить числитель на знаменатель. Числитель вычислять в данном примере нет необходимости, это число 9. Вычислим значение знаменателя: Можно произвести вычисления в столбик, тогда получим: Либо перевести дробь к простому виду: 4,5 • 2,5 = 4½ • 2 ½ = 9 / 2 • 5 / 2 = 45 / 4 Последний случай предпочтительней, так как для дальнейшей операции – деления числителя на знаменатель задача упрощается. Делим числитель на знаменатель, умножая числитель на перевернутую дробь в знаменателе: 9 / ( 45 / 4 ) = ( 9 / 1 ) • ( 4 / 45 ) = ( 9 • 4 ) / (1 • 45 ) 9 и 45 можно сократить на 9: ( 9 • 4 ) / (1 • 45 ) = ( 1 • 4 )/ (1 • 5 ) = 4 / 5 = 8 / 10 = 0,8 pазбирался: Даниил Романович | обсудить разбор | оценить Урок 40 Бесплатно Десятичная запись дробных чиселВ реальной жизни часто приходится использовать дробные величины, не всегда удается измерить и охарактеризовать величины целым числом. В различных областях деятельности человека возникает необходимость решать практические и теоретические задачи, используя дробные значения, знать правила сложения, вычитания, умножения и деления дробей. Однако, работать с обыкновенными дробями, которые нам уже хорошо известны, зачастую не очень удобно. Сегодня на уроке мы рассмотрим десятичную запись дробных чисел. Выясним, что называют десятичной дробью, как ее правильно записать и прочитать. Научимся переводить обыкновенную дробь в десятичную и обратно. Десятичные дроби. Чтение и запись десятичных дробейСуществуют два вида десятичных дробей обыкновенные и десятичные. Об обыкновенной дроби нам многое уже известно. Обыкновенные дроби делятся на правильные и неправильные. Правильными называют дроби, в которой числитель меньше знаменателя. Дроби, в которых числитель больше знаменателя или равен ему, называют неправильной дробью. Неправильная дробь в свою очередь может быть записана в виде смешанного числа, которое представляет собой сумму натурального (целой части) и дробного числа (дробной части). Обыкновенную дробь записывают с помощью двух чисел, разделенных дробной чертой (наклонной или горизонтальной). Число, стоящее над дробной чертой, называют числителем. Число, стоящее под дробной чертой, называют знаменателем. Давайте выясним, а какие же дроби называют десятичными, как их правильно записывать и читать. Обратите внимание на рисунок. На нем изображен простейший измерительный инструмент- линейка. С помощью линейки несложно определить линейные размеры небольших объектов. Известно, что один сантиметр содержит десять миллиметров, т.е. 1 см = 10 мм. Следовательно, один миллиметр- это доля сантиметра, т.е. одна десятая его часть. В виде дроби один миллиметр можно записать так: \(\mathbf<\frac<1><\color Дробь \(\mathbf<\frac<1><\color Рассмотрим еще одну ситуацию. С помощью этой же линейки изобразили отрезок длиной 2 см 5 мм. Выразим данную длину отрезка в сантиметрах. 2 см- это два целых сантиметровых отрезка. Давайте разберемся, что представляют собой 5 мм. 5 мм- это часть сантиметра. Так как 1 миллиметр- это десятая часть сантиметра, т.е. одна часть из десяти (\(\mathbf<\frac<1><\color Дробь \(\mathbf<\frac<5><10>>\) в данном случае означает, что один сантиметр разделили на десять равных частей и из них взяли пять таких частей. В итоге мы имеем два целых сантиметра, да еще пять десятых сантиметра: \(\mathbf<2\frac<5><10>>\). \(\mathbf<2\frac<5><10>>\)- это смешанное число, читается оно так: «две целых пять десятых». Число 2 показывает число целых частей, а правильная дробь \(\mathbf<\frac<5><10>>\)- дробную часть. Такую запись числа, где целая часть числа отделяется запятой от дробной, называют десятичной записью, а само число десятичной дробью. Запятую, которая разделяет целую и дробную часть числа называют десятичной запятой. Десятичные дроби подобно смешанному числу содержат две части (целую и дробную). В таком случае, длину отрезка, равную \(\mathbf<2\frac<5><10>>\) см, можем представить в виде десятичной дроби, как 2,5 см. Здесь число 2— это целая часть десятичной дроби, показывает число целых частей, а число 5— это числитель дробной части смешанного числа, представляет собой дробную часть десятичной дроби. Отрезок длинной \(\mathbf<2\frac<5><10>>\) см и длинной 2,5 см это один и тот же отрезок. Как мы видим, форма записи этих двух чисел разная, но по своей сути они выражают одно и тоже число. Мы можем смело утверждать, что десятичные дроби- это просто форма записи обыкновенных дробей. Как выглядит смешанное число в виде десятичной дроби теперь нам ясно, а как записать правильную обыкновенную дробь в форме десятичной дроби, ведь целая часть у правильной обыкновенной дроби отсутствует, т.е. равна нулю? Например, правильная обыкновенная дробь \(\mathbf<\frac<5><10>>\) в виде десятичного числа будет выглядеть следующим образом: \(\mathbf<\frac<5> <10>= 0,5>\). Как правильно прочитать десятичную дробь? Это совсем не сложно. Смешанное число \(\mathbf<1\frac<2><10>>\) состоит из целой части (число 1) и дробной части (правильная дробь \(\mathbf<\frac<2><10>>\)). Смешанное число \(\mathbf<\color Числу \(\mathbf<\color У правильной обыкновенной дроби отсутствует целая часть, именно отсутствие целой части и обозначает ноль, стоящий перед десятичной запятой. У меня есть дополнительная информация к этой части урока! Стоит отметить, что десятым долям соответствует один символ после запятой (\(\mathbf<0,1 = \frac<1><10>>\)), сотым- соответствует два знака (\(\mathbf<0,01 = \frac<1><100>>\)), тысячным- три знака после десятичной запятой (\(\mathbf<0,001 = \frac<1><1000>>\)). С давних времен умение выполнять различные математические операции и вести расчеты считалось очень ценным умением. Часто приходилось измерять различные величины: длину, ширину, площади и объемы, время, массу, выгодно вести торговые дела. С течением времени возникала все большая потребность в точных измерениях и вычислениях. Не всегда удавалось однозначно выразить величину одним лишь натуральным числом. Люди вынуждены были придумать дробную систему для измерения и вычисления величин. Человечество преодолело огромный путь, чтобы отыскать удобный вариант записи дробных чисел. Первые знания о дробях были связаны с обыкновенными дробями, позже появились десятичные дроби. История возникновения обыкновенных дробей берет свое начало в Древнем Египте, а десятичные дроби появились в Древнем Китае. У меня есть дополнительная информация к этой части урока! Десятичная запись дроби создавалась как более точный, удобный и компактный способ изображения дробных чисел. Десятичную дробь в Китае стали использовать примерно с III века до н.э. первоначально для расчета веса и объема. С течением времени они все больше и больше стали проникать в науку. В Древнем Китае уже пользовались десятичной системой мер, в связи с этим дроби обозначали словами, используя меры длины. Независимо от древнекитайских математиков десятичными дробями занимались арабские ученые. В X веке арабский математик Ал-Уклидиси написал «Книгу разделов о индийской математике». Он описывал различные действия с числами, которые были записаны в десятичной системе. В его работе были представлены первые десятичные дроби, записанные с помощью цифр и знаков. Попытка Ал-Уклидиси введения десятичных дробей не была успешной, его работа осталась незамеченной. В начале ХV века самаркандский математик и астроном Джемшид Гияседин аль-Каши в своем трактате (1427 г.) представил полную теорию десятичных дробей. Подробно описал правила действия с десятичными дробями. В своей работе Аль-Каши предложил использовать новый способ записи десятичных дробей. Он записывал целую и дробную часть числа в одной строке, при этом одна часть отличалась от другой цветом шрифта. Иногда ученый отделял целую часть от дробной вертикальной чертой, а над цифрами писал их разряды. Европейцы с трудами Древних китайцев и арабских ученых не были знакомы. В Европе десятичная форма записи дробей появилась в научных работах математиков с ХIII века. Так, например, около 1350 г. европейский математик и астролог Иммануил Бонфис первым в Европе описал общую теорию десятичных дробей, но широкого распространения эта теория не получила. Позже итальянский математик и механик Иордан Неморарий в своем труде «Арифметика» высказал мысль о построении системы десятичных дробей. Затем в XVI веке французский ученый Франсуа Виет активно продвигает десятичные дроби в научное использование. Благодаря ему десятичные дроби стали широко использоваться в научных расчетах. Ученый в 1579 г. опубликовал свой труд «Математический канон». В нем Франсуа Виет представил таблицы, при составлении которых он использовал десятичные дроби. Однозначного представления о том, как должны быть записаны и обозначаться десятичные дроби, у него не было. В своих работах он иногда целую и дробную часть отделял вертикальной чертой, иногда различным по жирности начертанием, порой цифры дробной части он делал меньше, чем цифры целой части. Широкое применение десятичных дробей как в научной работе, так и в повседневной жизни стали использовать благодаря голландскому ученому Симону Стевину в конце XVI веке. В своем научном в 1585 г. труде «Десятая» он подробно изложил теорию использования десятичных дробей и правила действия с десятичными дробями в различных областях практической деятельности человека. Он предложил записывать целую и дробную часть дробного числа в одну строку, нумеруя цифры при этом. Он разделял две части дроби нулем, обведенным в кружок. Например, число 2,485 в записи Симона Стевина выглядело так: 2 ⓪ 4 ① 8 ② 5 ③ Сам математик и его труд «Десятая» быстро стали популярными в Европе. Именно Симона Стевина считают изобретателем десятичных дробей. Современная запись десятичных дробей, где целая и дробная часть отделяется запятой, впервые была предложена в 1592 г. В Англии вместо запятой стали использовать точку. В 1617 г. шотландский математик Джон Непер предложил оба разделительных знака (и точку и запятую) считать равноценными. Англия, США и Канада до сих пор в записи десятичной дроби, чтобы разделить целую и дробную часть, ставят не запятую, а точку. В России впервые систематизированные сведения о десятичных дробях изложил математик Леонтий Филиппович Магнитский в своем учебнике по арифметике (1701 г.) Пройти тест и получить оценку можно после входа или регистрации Десятичные дробиМы уже говорили, что дроби бывают обыкновенные и десятичные. На данный момент мы немного изучили обыкновенные дроби. Мы узнали, что обыкновенные дроби бывают правильные и неправильные. Также мы узнали, что обыкновенные дроби можно сокращать, складывать, вычитать умножать и делить. И ещё мы узнали, что бывают так называемые смешанные числа, которые состоят из целой и дробной части. Мы ещё не до конца изучили обыкновенные дроби. Есть немало тонкостей и деталей, о которых следует поговорить, но уже сегодня мы начнём изучать десятичные дроби, поскольку обыкновенные и десятичные дроби достаточно часто приходится сочетать. То есть при решении задач приходиться работать с обоими видов дробей. Этот урок возможно покажется сложным и непонятным. Это вполне нормально. Такого рода уроки требуют, чтобы их именно изучали, а не просматривали поверхностно. Выражение величин в дробном видеИногда удобно бывает показать что-либо в дробном виде. Например, одна десятая часть дециметра записывается так: Это выражение означает, что один дециметр был разделён на десять равных частей, и от этих десяти частей была взята одна часть. А одна часть из десяти в данном случае равна одному сантиметру: Рассмотрим следующий пример. Пусть требуется показать 6 см и ещё 3 мм в сантиметрах в дробном виде. Итак, 6 целых сантиметров у нас уже есть: Но осталось еще 3 миллиметра. Как показать эти 3 миллиметра, при этом в сантиметрах? На помощь приходят дроби. Один сантиметр это десять миллиметров. Три миллиметра это три части из десяти. А три части из десяти записываются как Выражение В результате имеем шесть целых сантиметров и три десятых сантиметра: Дроби, в знаменателе которых присутствуют числа 10, 100, 1000 можно записывать без знаменателя. Сначала пишут цéлую часть, а потом числитель дробной части. Целая часть отделяется от числителя дробной части запятой. Например, запишем Целая часть записана. Сразу же после написания целой части ставим запятую: И теперь записываем числитель дробной части. В смешанном числе Любое число, которое представляется в таком виде, называется десятичной дробью. Поэтому показать 6 см и ещё 3 мм в сантиметрах можно с помощью десятичной дроби: Выглядеть это будет следующим образом: На самом деле десятичные дроби это те же самые обыкновенные дроби и смешанные числа. Особенность таких дробей заключается в том, что в знаменателе их дробной части содержатся числа 10, 100, 1000 или 10000. Как и смешанное число, десятичная дробь имеет цéлую часть и дробную. Например, в смешанном числе В десятичной дроби 6,3 целая часть это число 6, а дробная часть это числитель дроби Бывает и так, что обыкновенные дроби в знаменателе которых числа 10, 100, 1000 даны без целой части. Например, дробь Читается как «ноль целых, пять десятых». Перевод смешанных чисел в десятичные дробиКогда мы записываем смешанные числа без знаменателя, мы тем самым перевóдим их в десятичные дроби. При переводе обыкновенных дробей в десятичные дроби нужно знать несколько моментов, о которых мы сейчас поговорим. После того как записана целая часть, обязательно нужно посчитать количество нулей в знаменателе дробной части, поскольку количество нулей дробной части и количество цифр после запятой в десятичной дроби должно быть одинаковым. Что это значит? Рассмотрим следующий пример: перевести смешанное число Сначала записываем целую часть и ставим запятую: И можно бы сразу записать числитель дробной части и десятичная дробь готова, но обязательно нужно посчитать сколько нулей содержится в знаменателе дробной части. Итак, посчитаем количество нулей в дробной части смешанного числа Таким образом, смешанное число «Три целых, две десятых» «Десятых» потому что в дробной части смешанного числа Пример 2. Перевести смешанное число Записываем цéлую часть и ставим запятую: И можно бы сразу записать числитель дробной части и получить десятичную дробь 5,3 но правило говорит, что после запятой должно быть столько цифр сколько нулей в знаменателе дробной части смешанного числа В таких случаях числитель дробной части нужно немного видоизменить: добавить ноль перед числителем, то есть перед числом 3 Теперь можно довести дело до конца. Записываем после запятой числитель дробной части: Видим, что количество цифр после запятой и количество нулей в знаменателе дробной части смешанного числа Десятичная дробь 5,03 читается так: «Пять целых, три сотых» «Сотых» потому что в знаменателе дробной части смешанного числа Пример 3. Перевести смешанное число Из предыдущих примеров мы узнали, что для успешного перевода смешанного числа в десятичную дробь, количество цифр в числителе дробной части и количество нулей в знаменателе дробной части должно быть одинаковым. Перед переводом смешанного числа В первую очередь смóтрим на количество нулей в знаменателе дробной части. Видим, что там три нуля: Наша задача организовать в числителе дробной части три цифры. Одна цифра у нас уже есть — это цифра 2. Осталось добавить ещё две цифры. Ими будут два нуля. Добавим их перед цифрой 2. В результате количество нулей в знаменателе и количество цифр в числителе станет одинаковым: Теперь можно заняться переводом этого смешанного числа в десятичную дробь. Записываем сначала цéлую часть и ставим запятую: и сразу записываем числитель дробной части Видим, что количество цифр после запятой и количество нулей в знаменателе дробной части смешанного числа Десятичная дробь 3,002 читается так: «Три целых, две тысячных» «Тысячных» потому что в знаменателе дробной части смешанного числа Перевод обыкновенных дробей в десятичные дробиОбыкновенные дроби, у которых в знаменателе числа 10, 100, 1000 или 10000, тоже можно перевести в десятичные дроби. Поскольку у обыкновенной дроби целая часть отсутствует, сначала записывают 0, затем ставят запятую и записывают числитель дробной части. Здесь также количество нулей в знаменателе и количество цифр в числителе должно быть одинаковым. Поэтому следует быть внимательным. Пример 1. Перевести обыкновенную дробь Целая часть отсутствует, значит сначала записываем 0 и ставим запятую: Теперь смóтрим на количество нулей в знаменателе. Видим, что там один ноль. И в числителе одна цифра. Значит можно спокойно продолжить десятичную дробь, записав после запятой цифру 5 В полученной десятичной дроби 0,5 количество цифр после запятой и количество нулей в знаменателе дроби Десятичная дробь 0,5 читается так: «Ноль целых, пять десятых» Пример 2. Перевести обыкновенную дробь Целая часть отсутствует. Записываем сначала 0 и стáвим запятую: Теперь смóтрим на количество нулей в знаменателе. Видим, что там два нуля. А в числителе только одна цифра. Чтобы сделать количество цифр и количество нулей одинаковым, добавим в числителе перед цифрой 2 один ноль. Тогда дробь примет вид В полученной десятичной дроби 0,02 количество цифр после запятой и количество нулей в знаменателе дроби Десятичная дробь 0,02 читается так: «Ноль целых, две сотых». Пример 3. Перевести обыкновенную дробь Записываем 0 и стáвим запятую: Теперь посчитаем количество нулей в знаменателе дроби Теперь можно продолжить десятичную дробь. Записываем после запятой числитель дроби В полученной десятичной дроби 0,00005 количество цифр после запятой и количество нулей в знаменателе дроби Десятичная дробь 0,00005 читается так: «Ноль целых, пять стотысячных». Перевод неправильных дробей в десятичную дробьНеправильная дробь это дробь, у которой числитель больше знаменателя. Бывают неправильные дроби, у которых в знаменателе содержатся числа 10, 100, 1000 или 10000. Такие дроби можно переводить в десятичные. Но перед переводом в десятичную дробь, у таких дробей необходимо выделять цéлую часть. Пример 1. Перевести неправильную дробь Дробь Итак, выделим целую часть в неправильной дроби Посмóтрим на этот рисунок и соберём новое смешанное число, подобно детскому конструктору. Частное 11 будет целой частью, остаток 2 — числителем дробной части, делитель 10 — знаменателем дробной части: Мы получили смешанное число Теперь посчитаем количество нулей в знаменателе дробной части. Видим, что там один ноль. И в числителе дробной части одна цифра. Значит количество нулей в знаменателе дробной части и количество цифр в числителе дробной части одинаково. Это даёт нам возможность сразу записать после запятой числитель дробной части: Значит, неправильная дробь Десятичная дробь 11,2 читается так: «Одиннадцать целых, две десятых». Пример 2. Перевести неправильную дробь Это неправильная дробь, поскольку числитель больше знаменателя. Но её можно перевести в десятичную дробь, поскольку в знаменателе содержится число 100. В первую очередь выделим целую часть этой дроби. Для этого разделим уголком 450 на 100: Соберём новое смешанное число — получим Теперь посчитаем количество нулей в знаменателе дробной части и количество цифр в числителе дробной части. Видим, что количество нулей в знаменателе и количество цифр в числителе одинаково. Это даёт нам возможность сразу записать числитель дробной части после запятой: Значит неправильная дробь При решении задач, если в конце десятичной дроби оказываются нули, их можно отбросить. Давайте и мы отбросим ноль в нашем ответе. Тогда мы получим 4,5 Это одна из интересных особенностей десятичных дробей. Она заключается в том, что нули которые стоят в конце дроби, не придают этой дроби никакого веса. Другими словами, десятичные дроби 4,50 и 4,5 равны и между ними можно поставить знак равенства: Возникает вопрос «а почему так происходит?» Ведь на вид 4,50 и 4,5 разные дроби. Весь секрет кроется в основном свойстве дроби, котором мы изучали ранее. Мы попробуем доказать, почему равны десятичные дроби 4,50 и 4,5, но после изучения следующей темы, которая называется «перевод десятичной дроби в смешанное число». Перевод десятичной дроби в смешанное числоЛюбая десятичная дробь может быть обратно переведена в смешанное число. Для этого достаточно уметь читать десятичные дроби. Например, переведём 6,3 в смешанное число. 6,3 это шесть целых и три десятых. Записываем сначала шесть целых: и рядом три десятых: Пример 2. Перевести десятичную дробь 3,002 в смешанное число 3,002 это три целых и две тысячных. Записываем сначала три целых и рядом записываем две тысячных: 3 Пример 3. Перевести десятичную дробь 4,50 в смешанное число 4,50 это четыре целых и пятьдесят сотых. Записываем четыре целых и рядом пятьдесят сотых: Кстати, давайте вспомним последний пример из предыдущей темы. Мы сказали, что десятичные дроби 4,50 и 4,5 равны. Также мы сказали, что ноль можно отбросить. Докажем, что десятичные 4,50 и 4,5 равны. Для этого переведем обе десятичные дроби в смешанные числа. После перевода в смешанное число десятичная дробь 4,50 обращается в Имеем два смешанных числа Теперь имеем две дроби Давайте разделим числитель и знаменатель первой дроби Получили Перевод десятичной дроби в обыкновенную дробьЛюбая десятичная дробь может быть обратно переведена в обыкновенную дробь. Для этого опять же достаточно уметь читать десятичные дроби. Например, переведём 0,3 в обыкновенную дробь. 0,3 это ноль целых и три десятых. Записываем сначала ноль целых: и рядом три десятых 0 Пример 2. Перевести десятичную дробь 0,02 в обыкновенную дробь. 0,02 это ноль целых и две сотых. Ноль не записываем, поэтому сразу записываем две сотых Пример 3. Перевести 0,00005 в обыкновенную дробь 0,00005 это ноль целых и пять сто тысячных. Ноль не записываем, поэтому сразу записываем пять сто тысячных Пример 4. Перевести 3,5 в обыкновенную дробь Сначала переведём данную десятичную дробь в смешанное число: Теперь смешанное число Пример 5. Перевести 1,25 в обыкновенную дробь Сначала переведём данную десятичную дробь в смешанное число: Теперь смешанное число Понравился урок? Возникло желание поддержать проект? 37 thoughts on “Десятичные дроби”все круто, понятно и доступно. Спасибо за сайт! Всё очень понятно. Не понимал что такое дробь уже с пятого класса (щя 2 курс колледжа), прочитав на сайте всё понял, спасибо вам. Огромное спаасибо! Просто, интересно, и очень нужно! Успехов и радости в жизни! Я не понимаю как перевести обыкновенные дробь в десятичную с некруглым знаменателем А что значит десятичная дробь с некруглым знаменателем? У десятичной дроби всегда круглый знаменатель — 10, 100, 1000. Чтобы перевести некруглый знаменатель в десятичный, нужно найти НОК с этим круглым числом. И множить… Перевод дроби в десятичнуюПеревод дроби в десятичную дробь необходим в первую очередь для удобства восприятия числа, т.к. человек в ряде случаев склонен считывать информацию в том виде, к которому он привык ещё с первого знакомства с математикой. Различия десятичных и обычных дробейДля начала давайте вспомним, чем они отличаются друг от друга. Обыкновенная дробь– это дробь, представленная в виде a/b Десятичная же дробь представляется рядом цифр, которые располагаются в некоем числе до и после точки, т.е. 0.5, 1.5, 10.33, –110.58 и т.д. Например, обыкновенная дробь 1/2 при переводе в десятичную превращается в число 0.5. Необходимо заметить, что для перевода обыкновенной дроби в конечную десятичную её знаменатель в обязательном порядке должен быть подвержен разложению только на множители 2 и/или 5n раз (1 как множитель не учитываем); но если, кроме указанных множителей, появляются другие (например, 3 или 4), такую дробь уже нельзя назвать конечной, потому как она становится бесконечной десятичной. Дана дробь: Немногим усложним её для лучшего понимания и дальше будем работать со следующей формой записи оной 7/5, т.е. превратим смешанную дробь в неправильную; в знаменателе данной дроби уже присутствует множитель 5– следовательно, сама она конечная. Пожалуй, самый простой способ перевода обыкновенной дроби в десятичную вручную – умножить заданный знаменатель на такое число, чтобы получилось 100 (к слову, 100 можно разложить на следующие множители: 2, 2, 5 и 5). Соответственно, на такое же число нужно будет после умножить и числитель. Находим, что заданный в примере знаменатель можно умножить на 20, чтобы в итоге получить 100. Тогда имеем следующее: Заметим, что остановить вычисления можно было уже на дроби тогда, зная, что число 100 содержит в себе два нуля, просто передвигаемся на два знака [с конца] влево в числителе и ставим точку, т.е. 140 = 1.40 = 1.4. Проверяем, правильно ли мы посчитали. Введём в соответствующие поля нашего калькулятора обыкновенной дроби В десятичную заданные значения (1, 2 и 5) и получим искомый ответ, т.е. 1.4. Как перевести десятичную дробь в обыкновеннуюВот, казалось бы, перевод десятичной дроби в обычную — элементарная тема, но многие ученики её не понимают! Поэтому сегодня мы подробно рассмотрим сразу несколько алгоритмов, с помощью которых вы разберётесь с любыми дробями буквально за секунду. Напомню, что существует как минимум две формы записи одной и той же дроби: обыкновенная и десятичная. Десятичные дроби — это всевозможные конструкции вида 0,75; 1,33; и даже −7,41. А вот примеры обыкновенных дробей, которые выражают те же самые числа: Сейчас разберёмся: как от десятичной записи перейти к обычной? И самое главное: как сделать это максимально быстро? Основной алгоритмНа самом деле существует как минимум два алгоритма. И мы сейчас рассмотрим оба. Начнём с первого — самого простого и понятного. Чтобы перевести десятичную дробь в обыкновенную, необходимо выполнить три шага: Важное замечание по поводу отрицательных чисел. Если в исходном примере перед десятичной дробью стоит знак «минус», то и на выходе перед обыкновенной дробью тоже должен стоять «минус». Вот ещё несколько примеров: Особое внимание хотелось бы обратить на последний пример. Как видим, в дроби 0,0025 присутствует много нулей после запятой. Из-за этого приходится аж целых четыре раза умножать числитель и знаменатель на 10. Можно ли как-то упростить алгоритм в этом случае? Конечно, можно. И сейчас мы рассмотрим альтернативный алгоритм — он чуть более сложен для восприятия, но после небольшой практики работает намного быстрее стандартного. Более быстрый способВ данном алгоритме также 3 шага. Чтобы получить обычную дробь из десятичной, нужно выполнить следующее: Вот и всё! На первый взгляд, эта схема сложнее предыдущей. Но на самом деле он и проще, и быстрее. Судите сами: Наконец, последний пример: Особенность этой дроби — наличие целой части. Поэтому на выходе у нас получается неправильная дробь 47/25. Можно, конечно, попытаться разделить 47 на 25 с остатком и таким образом вновь выделить целую часть. Но зачем усложнять себе жизнь, если это можно сделать ещё на этапе преобразований? Что ж, разберёмся. Что делать с целой частьюНа самом деле всё очень просто: если мы хотим получить правильную дробь, то необходимо убрать из неё целую часть на время преобразований, а затем, когда получим результат, вновь дописать её справа перед дробной чертой. Например, рассмотрим то же самое число: 1,88. Забьём на единицу (целую часть) и посмотрим на дробь 0,88. Она легко преобразуется: Затем вспоминаем про «утерянную» единицу и дописываем её спереди: Вот и всё! Ответ получился тем же самым, что и после выделения целой части в прошлый раз. Ещё парочка примеров: В этом и состоит прелесть математики: каким бы путём вы не пошли, если все вычисления выполнены правильно, ответ всегда будет одним и тем же.:) В заключение хотел бы рассмотреть ещё один приём, который многим помогает. Преобразования «на слух»Давайте задумаемся о том, что вообще такое десятичная дробь. Точнее, как мы её читаем. Например, число 0,64 — мы читаем его как «ноль целых, 64 сотых», правильно? Ну, или просто «64 сотых». Ключевое слово здесь — «сотых», т.е. число 100. А что насчёт 0,004? Это же «ноль целых, 4 тысячных» или просто «четыре тысячных». Так или иначе, ключевое слово — «тысячных», т.е. 1000. Ну и что в этом такого? А то, что именно эти числа в итоге «всплывают» в знаменателях на втором этапе алгоритма. Т.е. 0,004 — это «четыре тысячных» или «4 разделить на 1000»: Попробуйте потренироваться сами — это очень просто. Главное — правильно прочесть исходную дробь. Например, 2,5 — это «2 целых, 5 десятых», поэтому А какое-нибудь 1,125 — это «1 целая, 125 тысячных», поэтому \[\begin Таким образом, любая степень десятки раскладывается лишь на множители 2 и 5 — именно эти множители нужно искать и в числителе, чтобы в итоге всё сократилось. На этом урок окончен. Переходим к более сложной обратной операции — см. «Переход от обыкновенной дроби к десятичной». Перевод обыкновенной дроби в десятичную дробь и обратно, правила, примеры.В этой статье мы разберем, как осуществляется перевод обыкновенных дробей в десятичные дроби, а также рассмотрим обратный процесс – перевод десятичных дробей в обыкновенные дроби. Здесь мы озвучим правила обращения дробей и приведем подробные решения характерных примеров. Навигация по странице. Перевод обыкновенных дробей в десятичные дробиОбозначим последовательность, в которой мы будем разбираться с переводом обыкновенных дробей в десятичные дроби. После этого мы пойдем дальше и покажем, как любую обыкновенную дробь (не только со знаменателями 10, 100, … ) записать в виде десятичной дроби. При таком обращении обыкновенных дробей получаются как конечные десятичные дроби, так и бесконечные периодические десятичные дроби. Теперь обо всем по порядку. Перевод обыкновенных дробей со знаменателями 10, 100, … в десятичные дробиНекоторые правильные обыкновенные дроби перед переводом в десятичные дроби нуждаются в «предварительной подготовке». Это касается обыкновенных дробей, количество цифр в числителе которых меньше, чем количество нулей в знаменателе. Например, обыкновенную дробь 2/100 нужно предварительно подготовить к переводу в десятичную дробь, а дробь 9/10 в подготовке не нуждается. «Предварительная подготовка» правильных обыкновенных дробей к переводу в десятичные дроби заключается в дописывании слева в числителе такого количества нулей, чтобы там общее количество цифр стало равно количеству нулей в знаменателе. Например, дробь После подготовки правильной обыкновенной дроби можно приступать к ее обращению в десятичную дробь. Рассмотрим применение этого правила при решении примеров. Переведите правильную обыкновенную дробь 37/100 в десятичную. Для закрепления навыков перевода правильных обыкновенных дробей с числителями 10, 100, … в десятичные дроби разберем решение еще одного примера. Запишите правильную дробь 107/10 000 000 в виде десятичной дроби. Разберем применение этого правила при решении примера. Переведите неправильную обыкновенную дробь 56 888 038 009/100 000 в десятичную дробь. Рассмотрим пример, при решении которого выполним все необходимые шаги для представления смешанного числа в виде десятичной дроби. Переведите смешанное число Запишем все решение кратко: Перевод обыкновенных дробей в конечные и бесконечные периодические десятичные дробиВ остальных случаях приходится использовать другой способ перевода обыкновенной дроби в десятичную, к рассмотрению которого мы и переходим. Для обращения обыкновенной дроби в десятичную дробь выполняется деление числителя дроби на знаменатель, числитель предварительно заменяется равной ему десятичной дробью с любым количеством нулей после десятичной запятой (об этом мы говорили в разделе равные и неравные десятичные дроби). При этом деление выполняется так же, как деление столбиком натуральных чисел, а в частном ставится десятичная запятая, когда заканчивается деление целой части делимого. Все это станет понятно из решений примеров, приведенных ниже примеров. Переведите обыкновенную дробь 621/4 в десятичную дробь. Так мы добрались до десятичной запятой в делимом, а остаток при этом отличен от нуля. В этом случае в частном ставим десятичную запятую, и продолжаем деление столбиком, не обращая внимания на запятые: Для закрепления материала рассмотрим решение еще одного примера. Переведите обыкновенную дробь 21/800 в десятичную дробь. Запишите обыкновенную дробь 19/44 в виде десятичной дроби. Для перевода обыкновенной дроби в десятичную выполним деление столбиком: В заключение этого пункта разберемся, какие обыкновенные дроби можно перевести в конечные десятичные дроби, а какие – только в периодические. Пусть перед нами находится несократимая обыкновенная дробь (если дробь сократимая, то предварительно выполняем сокращение дроби), и нам нужно выяснить, в какую десятичную дробь ее можно перевести – в конечную или периодическую. Обыкновенные дроби не переводятся в бесконечные непериодические десятичные дробиИнформация предыдущего пункта порождает вопрос: «Может ли при делении числителя дроби на знаменатель получиться бесконечная непериодическая дробь»? Ответ: нет. При переводе обыкновенной дроби может получиться либо конечная десятичная дробь, либо бесконечная периодическая десятичная дробь. Поясним, почему это так. Других вариантов быть не может, следовательно, при обращении обыкновенной дроби в десятичную дробь не может получиться бесконечная непериодическая десятичная дробь. Из приведенных в этом пункте рассуждений также следует, что длина периода десятичной дроби всегда меньше, чем значение знаменателя соответствующей обыкновенной дроби. Перевод десятичных дробей в обыкновенные дробиТеперь разберемся, как перевести десятичную дробь в обыкновенную. Начнем с перевода конечных десятичных дробей в обыкновенные дроби. После этого рассмотрим метод обращения бесконечных периодических десятичных дробей. В заключение скажем о невозможности перевода бесконечных непериодических десятичных дробей в обыкновенные дроби. Перевод конечных десятичных дробей в обыкновенные дробиРассмотрим решения примеров. Обратите десятичную дробь 3,025 в обыкновенную дробь. В знаменатель записываем цифру 1 и справа к ней дописываем 3 нуля, так как в исходной десятичной дроби после запятой находятся 3 цифры.
Выполните перевод десятичной дроби 0,0017 в обыкновенную дробь. В знаменатель записываем единицу с четырьмя нулями, так как в исходной десятичной дроби после запятой 4 цифры.
Рассмотрим пример перевода десятичной дроби в смешанное число. Представьте десятичную дробь 152,06005 в виде смешанного числа Число 152 до десятичной запятой есть целая часть искомого смешанного числа. На этом перевод конечной десятичной дроби 152,06005 в смешанное число закончен. Перевод периодических дробей в обыкновенные дробиЛюбую периодическую десятичную дробь можно перевести в обыкновенную дробь. На примерах разберем способ, позволяющий осуществить такой переход. Начнем с самых простых случаев, когда период дроби есть 0. Периодические дроби с периодом 0 можно заменить равными им конечными десятичными дробями, для этого достаточно отбросить все нули справа. Таким образом, перевод в обыкновенные дроби периодических дробей с периодом 0 сводится к обращению конечных десятичных дробей. Запишите периодическую дробь 3,75(0) в виде обыкновенной дроби. Напомним, что сумма членов бесконечно убывающей геометрической прогрессии с первым членом b и знаменателем q ( 0 ) равна Теперь можно рассмотреть решения нескольких примеров. Переведите периодическую дробь 0,(8) в обыкновенную дробь. Для закрепления материала разберем решение еще одного примера. Представьте бесконечную десятичную периодическую дробь 0,43(18) в обыкновенную дробь. Бесконечные непериодические десятичные дроби не переводятся в обыкновенные дробиВыше мы выяснили, что любая обыкновенная дробь переводится либо в конечную десятичную дробь, либо в периодическую десятичную дробь. Отсюда следует, что никакая бесконечная непериодическая десятичная дробь не может быть переведена в обыкновенную дробь, так как полученную обыкновенную дробь нельзя будет перевести обратно в эту бесконечную непериодическую дробь. Десятичные дробиПонятие десятичной дробиПрежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними. Дробь — это запись числа в математика, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которое можно представить число. Есть два формата записи: В обыкновенной дроби над чертой принято писать делимое, которое становится числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление. В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. По сути, десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так: Конечная десятичная дробь — это дробь, в которой количество цифр после запятой точно определено. Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой. Свойства десятичных дробейГлавное свойство десятичной дроби звучит так: если к десятичной дроби справа приписать один или несколько нулей — ее величина не изменится. Это значит, что если в вашей дроби куча нулей — их можно просто отбросить. Например: Обыкновенная и десятичная дробь — давние друзья. Вот, как они связаны: Обучение на курсах по математике — отличный способ закрепить полученные знания на практике и подтянуть сложные темы. Как записать десятичную дробьДавайте разберем на примерах, как записывается десятичная дробь. Небольшая напоминалка: сначала пишем целую часть, ставим запятую и после записываем числитель дробной части. Пример 1. Перевести обыкновенную дробь 16/10 в десятичную. Пример 2. Перевести 37/1000 в десятичную дробь. Ответ: 37/1000 = 0,037. Как читать десятичную дробьЧтобы учитель вас правильно понял, важно читать десятичные дроби грамотно. Сначала произносим целую часть с добавлением слова «целых», а потом дробную с обозначением разряда — он зависит от количества цифр после запятой:
Сохраняй наглядную картинку, чтобы быстрее запомнить. Преобразование десятичных дробейЧтобы ни одна задача не смутила вас своей формулировкой, важно знать, как преобразовывать десятичные дроби в другие виды. Сейчас научимся! Как перевести десятичную дробь в процентыУже в пятом классе задачки по математике намекают, что дроби как-то связаны с процентами. И это правда: процент — это одна сотая часть от любого числа, обозначают его значком %. Чтобы узнать, как перевести проценты в дробь, нужно убрать знак % и разделить наше число на 100, как в примере выше. А чтобы перевести десятичную дробь в проценты — умножаем дробь на 100 и добавляем знак %. Давайте на примере: Выразить дробь в процентах просто: сначала превратим её в десятичную дробь, а потом применим предыдущее правило. 2/5 = 0,4 8/25 = 0,32 Чтобы разрезать торт на равные кусочки и не обижать гостей, нужно всего-то запомнить соотношения частей и целого. Наглядная табличка — наш друг-помощник: Преобразование десятичных дробейДесятичная дробь — это число с остатком, где остаток стоит после целой части и разделяется запятой. Смешанная дробь — это тоже число с остатком, но остаток записывают в виде простой дроби (с черточкой). Чтобы переводить десятичные дроби в смешанные, не нужно запоминать особые алгоритмы. Достаточно понимать определения и правильно читать заданную дробь — этим школьники и занимаются в 5 классе. А теперь давайте потренируемся! Пример 1. Перевести 5,4 в смешанное число. Пример 2. Перевести 4,005 в смешанное число. Ответ: 4,005 = 4 1/200. Пример 3. Перевести 5,60 в смешанное число. Как перевести десятичную дробь в обыкновеннуюНе будем придумывать велосипед и рассмотрим самый простой способ превращения десятичной дроби в обыкновенную. Вот, как это сделать: Не забывайте про минус в ответе, если пример был про отрицательное число. Очень обидная ошибка! Действия с десятичными дробямиС десятичными дробями можно производить те же действия, что и с любыми другими числами. Рассмотрим самые распространенные на простых примерах. Как разделить десятичную дробь на натуральное числоПример 2. Разделить 183,06 на 45. Ответ: 183,06 : 45 = 4,068. Как разделить десятичную дробь на обыкновеннуюЧтобы разделить десятичную дробь на обыкновенную или смешанную, нужно представить десятичную дробь в виде обыкновенной, а смешанное число записать, как неправильную дробь. Пример 1. Разделить 0,25 на 3/4. Пример 2. Разделить 2,55 на 1 1/3. Ответ: 2,55 : 1 1/3 = 1 73/80. Как умножить десятичную дробь на обыкновеннуюЧтобы умножить десятичную дробь на обыкновенную или смешанную, используют два правила за 6 класс. При первом приводим десятичную дробь к виду обыкновенной и потом умножаем на нужное число. Во втором случае приводим обыкновенную или смешанную дробь в десятичную и потом умножаем. Пример 1. Умножить 2/5 на 0,8. Пример 2. Умножить 0,28 на 6 1/4. Ответ: 0,28 ∗ 6 1/4 = 0,8. 3 шага для преобразования десятичных дробей в дроби (и обратно)Видео: 3 шага для преобразования десятичных дробей в дроби (и обратно)Содержание:Не знаете, как преобразовать десятичные дроби в дроби? Или как переводить дроби в десятичные? Это проще, чем вы думаете! Продолжайте читать, чтобы узнать, как выполнять преобразование десятичной дроби в дробную. (включая то, почему вам нужно выполнять разные шаги, если у вас есть повторяющееся десятичное число), шаги для преобразования дробной части в десятичную, удобную диаграмму с обычными десятичными / дробными преобразованиями и советы по быстрой оценке конверсий. Как преобразовать десятичные дроби в дробиКак преобразовать десятичную дробь в дробь? Любую десятичную дробь, даже если она выглядит сложной, можно преобразовать в дробь; вам просто нужно выполнить несколько шагов. Ниже мы объясняем, как преобразовать как завершающие десятичные, так и повторяющиеся десятичные дроби в дроби. Преобразование завершающей десятичной дроби в дробьШаг 1Запишите десятичную дробь, разделенную на единицу. Шаг 2Затем вы хотите умножить верхнюю и нижнюю часть новой дроби на 10 для каждой цифры слева от десятичной точки. Шаг 3ПримерОкончательный ответ: <27>/ <250>$. Преобразование повторяющейся десятичной дроби в дробьВ нашем примере мы преобразуем 0,6667 в дробь. Шаг 1Пусть x равно повторяющемуся десятичному числу, которое вы пытаетесь преобразовать, и определите повторяющуюся цифру (а). Шаг 2Умножьте на любое необходимое значение 10, чтобы получить повторяющиеся цифры в левой части десятичной дроби. Шаг 3Затем мы хотим получить уравнение, в котором повторяющаяся цифра находится справа от десятичной дроби. Глядя на x = 0,6667, мы видим, что повторяющаяся цифра (6) уже находится справа от десятичной дроби, поэтому нам не нужно производить какое-либо умножение. Сохраним это уравнение как x = 0,6667. Шаг 4Теперь нам нужно найти x используя наши два уравнения, x = 0,667 и 10x = 6,667. x = <6>долл. США / <9>долл. США ПримерПреобразуйте 1,0363636 в дроби. Этот вопрос немного сложнее, но мы будем делать те же шаги, что и выше. Затем найдите повторяющиеся цифры в левой части десятичной дроби (опять же, вам нужен только один набор повторяющихся цифр слева). Это включает в себя перемещение десятичной дроби на три разряда вправо, поэтому обе стороны необходимо умножить на (10 x 3) или на 1000. Теперь поместите повторяющиеся цифры справа от десятичной дроби. Глядя на уравнение x = 1.0363636, вы можете видеть, что в настоящее время между десятичной и повторяющейся цифрами стоит ноль. Десятичную дробь нужно переместить на одно место, поэтому обе стороны нужно умножить на 10 x 1. Теперь используйте два уравнения: 1000x = 1036,363636 и 10x = 10,363636, чтобы найти x. x = <1026>долл. США / <990>долл. США Поскольку числитель больше знаменателя, это называется неправильной дробью. Иногда вы можете оставить дробь как неправильную дробь или вас могут попросить преобразовать ее в обычную дробь. Вы можете сделать это, вычтя 990/990 из дроби и сделав из нее 1, которая будет стоять рядом с дробью. x = 1 <36>долл. США / <990>долл. США $ <36>/ <990>$ можно упростить, разделив его на 18. Как преобразовать дроби в десятичныеОднако, если у вас нет доступа к калькулятору, вы все равно можете преобразовывать дроби в десятичные с помощью деления в столбик или получения знаменателя, кратного 10. В этом разделе мы объясним оба этих метода. Метод длинного деленияЗнаменатель как значение метода 10Шаг 1Мы хотим, чтобы знаменатель, в данном случае 8, равнялся 10. Мы можем сделать это, умножив дробь на 125, что даст нам <375>/ <1000>$. Шаг 2Затем мы хотим, чтобы знаменатель был равен 1, чтобы избавиться от дроби. Мы сделаем это, разделив каждую часть дроби на 1000, что означает перемещение десятичной дроби на три позиции влево. Обратите внимание, что этот метод работает только для дроби со знаменателем, который можно легко умножить до значения 10. Однако есть уловка, которую вы можете использовать, чтобы оценить значение дробей, которые нельзя преобразовать с помощью этого метода. Посмотрите на пример ниже. ПримерПреобразуйте ⅔ в десятичную дробь. Нет числа, на которое можно умножить 3, чтобы оно стало точным кратным 10, но вы можете приблизиться. 999 очень близко к 1000, поэтому давайте представим, что на самом деле это 1000, разделите каждую часть дроби на 1000 и переместите десятичную дробь 666 на три позиции влево, получив 0,666 Преобразование обычных десятичных чисел в дробныеНиже приведена диаграмма с обычным преобразованием десятичной дроби в дробную. Их не нужно запоминать, но зная хотя бы некоторые из них, вы сможете легко выполнять некоторые общие преобразования. Если вы пытаетесь преобразовать десятичную дробь или дробь и у вас нет калькулятора, вы также можете увидеть, к какому значению на этой диаграмме ближе всего это число, чтобы получить обоснованную оценку конверсии. Десятичный Дробная часть Резюме: Как преобразовать десятичную дробь в дробьЕсли вы пытаетесь преобразовать десятичную дробь в дробную, сначала вам нужно определить, является ли это конечным десятичным числом (один с концом) или повторяющимся десятичным числом (один с цифрой или цифрой, повторяющейся до бесконечности). Как только вы это сделаете, вы можете выполнить несколько шагов для преобразования десятичной дроби в дробную и для записи десятичных дробей в дроби. Чтобы быстро оценить преобразование десятичной дроби в дробную (или наоборот), вы можете взглянуть на нашу диаграмму распространенных преобразований и посмотреть, какое из них ближе всего к вашей цифре, чтобы получить приблизительное представление о его ценности преобразования. Что дальше?Хотите узнать самые быстрые и простые способы конвертировать градусы Фаренгейта в градусы Цельсия? Мы вас прикрыли! Ознакомьтесь с нашим руководством по лучшим способам преобразования Цельсия в градусы Фаренгейта (или наоборот). Вы изучаете логарифмы и натуральные логарифмы на уроках математики? У нас есть руководство по всем правила естественного журнала ты должен знать. Знаете ли вы, что вода имеет особую плотность? Ознакомьтесь с нашим руководством, чтобы узнать какая плотность воды и как может измениться плотность. Источники информации:
|

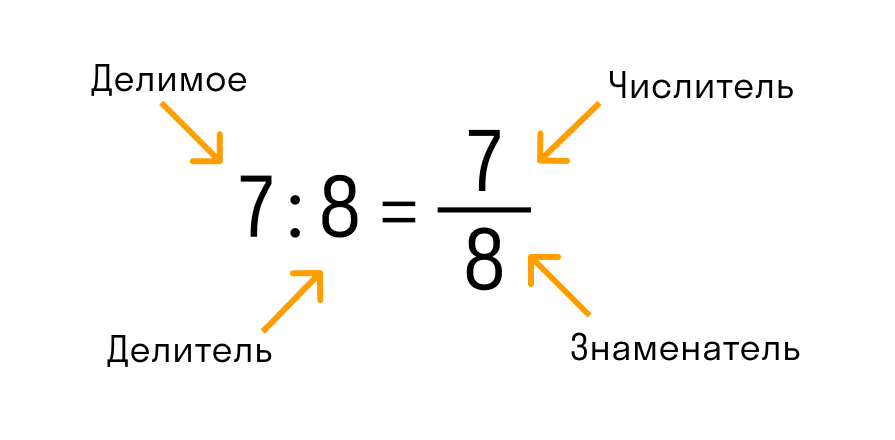
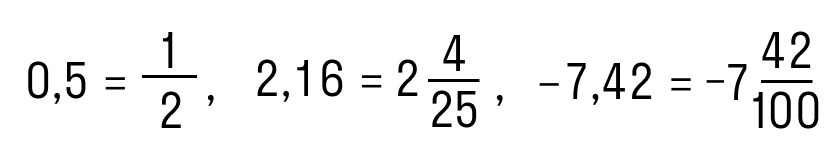
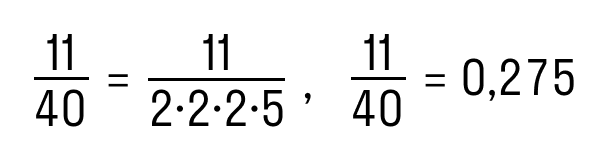
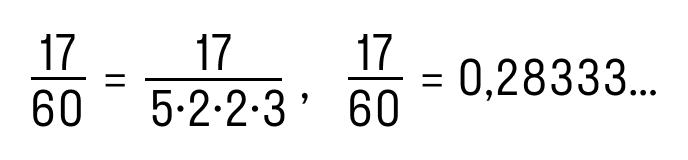
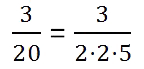
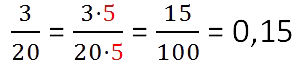
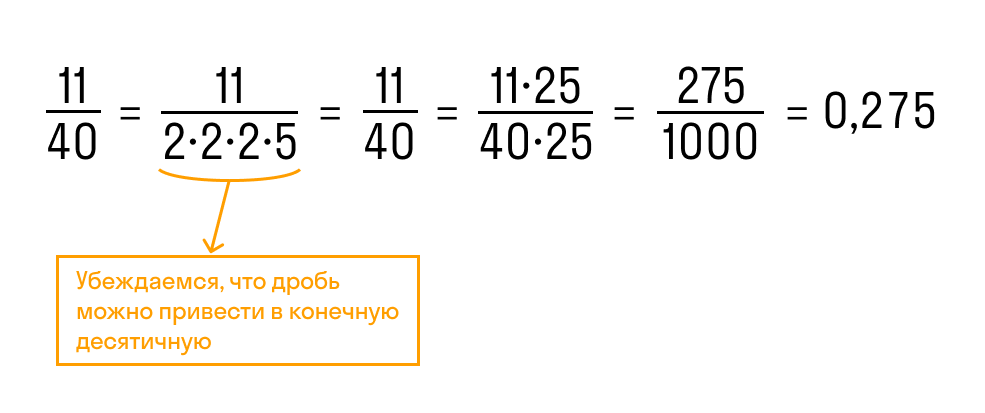
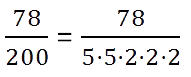
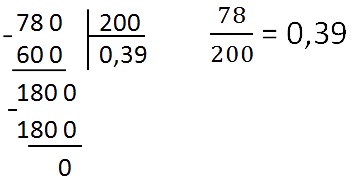
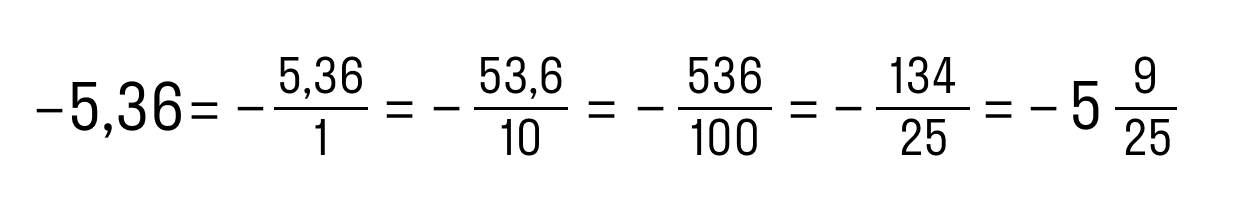
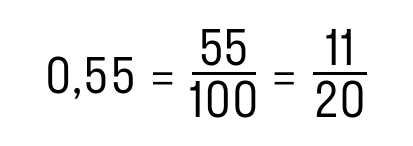
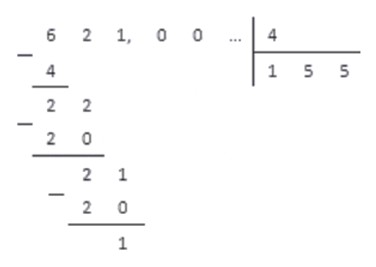
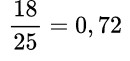
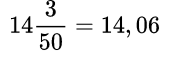
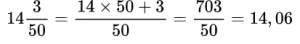
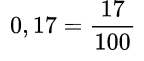
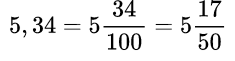
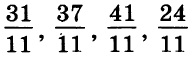 отмечено на прямой точкой.
отмечено на прямой точкой.

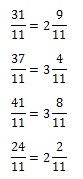
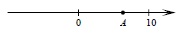
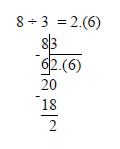
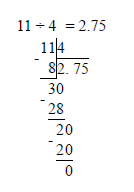












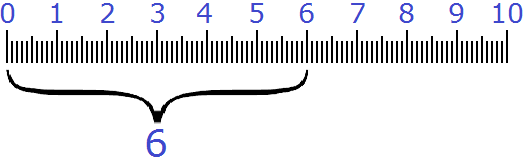
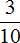 см
см
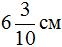
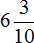 без знаменателя. Сначала записываем целую часть. Целая часть это 6
без знаменателя. Сначала записываем целую часть. Целая часть это 6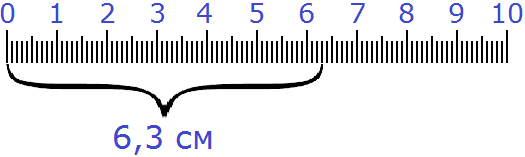
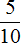 дана без целой части. Чтобы записать такую дробь как десятичную, сначала записывают 0, затем ставят запятую и записывают числитель дробной части. Дробь
дана без целой части. Чтобы записать такую дробь как десятичную, сначала записывают 0, затем ставят запятую и записывают числитель дробной части. Дробь 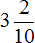 в десятичную дробь.
в десятичную дробь.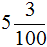 в десятичную дробь.
в десятичную дробь.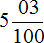
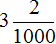 в десятичную дробь.
в десятичную дробь.
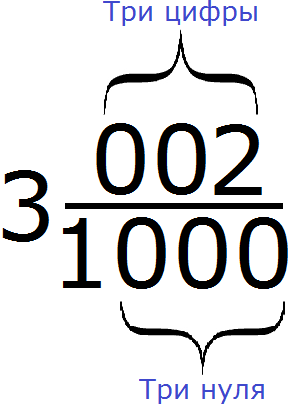
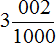 одинаково.
одинаково.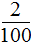 в десятичную дробь.
в десятичную дробь. . Теперь количество нулей в знаменателе и количество цифр в числителе одинаково. Значит можно продолжить десятичную дробь:
. Теперь количество нулей в знаменателе и количество цифр в числителе одинаково. Значит можно продолжить десятичную дробь: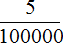 в десятичную дробь.
в десятичную дробь.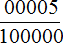
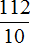 в десятичную.
в десятичную.

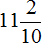 . Его и переведём в десятичную дробь. А как переводить такие числа в десятичные дроби мы уже знаем. Сначала записываем целую часть и ставим запятую:
. Его и переведём в десятичную дробь. А как переводить такие числа в десятичные дроби мы уже знаем. Сначала записываем целую часть и ставим запятую: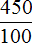 в десятичную дробь.
в десятичную дробь.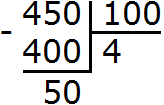
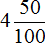 . Теперь переведём его в десятичную дробь. Записываем целую часть и ставим запятую:
. Теперь переведём его в десятичную дробь. Записываем целую часть и ставим запятую: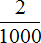
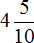

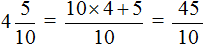
 и
и 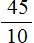 . Теперь вспоминаем основное свойство дроби, которое говорит о том, что при умножении (или делении) числителя и знаменателя дроби на одно и то же число, значение дроби не меняется.
. Теперь вспоминаем основное свойство дроби, которое говорит о том, что при умножении (или делении) числителя и знаменателя дроби на одно и то же число, значение дроби не меняется.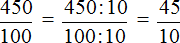

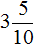 переведём в неправильную (обыкновенную) дробь:
переведём в неправильную (обыкновенную) дробь: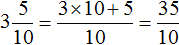
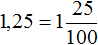
 переведём в неправильную (обыкновенную) дробь:
переведём в неправильную (обыкновенную) дробь: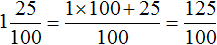
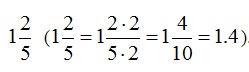

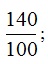
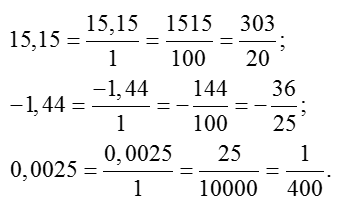 Примеры перехода от десятичной записи дробей к обычной
Примеры перехода от десятичной записи дробей к обычной после дописывания нулей будет иметь вид
после дописывания нулей будет иметь вид  .
. в десятичную дробь.
в десятичную дробь. .
.

 .
. .
. .
.