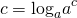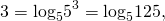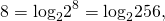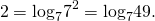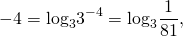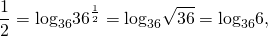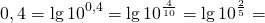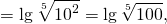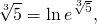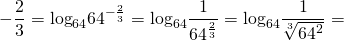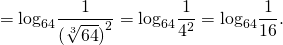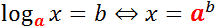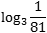Как из числа сделать логарифм
Как из числа сделать логарифм
Число в виде логарифма
Как представить число в виде логарифма?
Логарифм — это показатель степени, в которую надо возвести основание, чтобы получить число, стоящее под знаком логарифма.
Таким образом, чтобы представить некоторое число c в виде логарифма по основанию a, надо под знак логарифма поставить степень с тем же основанием, что и основание логарифма, а в показатель степени записать это число c:
В виде логарифма можно представить абсолютно любое число — положительное, отрицательное, целое, дробное, рациональное, иррациональное:
Чтобы в стрессовых условиях контрольной или экзамена не перепутать a и c, можно воспользоваться таким правилом для запоминания:
то, что внизу, идёт вниз, то, что вверху, идёт вверх.
Например, нужно представить число 2 в виде логарифма по основанию 3.
У нас есть два числа — 2 и 3. Эти числа — основание и показатель степени, которую мы запишем под знак логарифма. Остаётся определить, которое из этих чисел нужно записать вниз, в основание степени, а которое — вверх, в показатель.
Основание 3 в записи логарифма стоит внизу, значит, когда мы будем представлять двойку в виде логарифма по основанию 3, 3 также запишем вниз, в основание. 2 стоит выше тройки. И в записи степени двойку запишем выше тройки, то есть, в показатель степени:
Логарифмы и их свойства
Обычно определение логарифма дают очень сложно и запутанно. Мы постараемся сделать это очень просто и наглядно.
Для того, чтобы разобраться, что такое логарифм, давайте рассмотрим пример:
Все знакомы, что такое степень числа (если нет, то вам сюда). В таблице приведены различные степени числа 2. Глядя на таблицу, ясно, что, например, число 32 – это 2 в пятой степени, то есть двойка, умноженная на саму себя пять раз.
Теперь при помощи этой таблицы введем понятие логарифма.
Логарифм от числа 32 по основанию 2 (\(log_<2>(32)\)) – это в какую степень нужно возвести двойку, чтобы получить 32. Из таблицы видно, что 2 нужно возвести в пятую степень. Значит наш логарифм равен 5:
Аналогично, глядя в таблицу получим, что:
Естественно, логарифм бывает не только по основанию 2, а по любым основаниям больших 0 и неравных 1. Можете так же создавать таблицы для разных чисел. Но, конечно, со временем вы это будете делать в уме.
Теперь дадим определение логарифма в общем виде:
Логарифмом положительного числа \(b\) по основанию положительно числа \(a\) называется степень \(c\), в которую нужно возвести число \(a\), чтобы получить \(b\)
Но, конечно, вы часто будете сталкиваться не с такими простыми логарифмами, как в примерах с двойкой, а очень часто будет, что логарифм нельзя в уме посчитать. Действительно, что скажете про логарифм пяти по основанию два:
Как его посчитать? При помощи калькулятора. Он нам покажет, что такой логарифм равен иррациональному числу:
Или логарифм шести по основанию 4:
На уроках математики пользоваться калькулятором нельзя, поэтому на экзаменах и контрольных принято оставлять такие логарифмы в виде логарифма – не считая его, это не будет ошибкой!
Но иногда можно столкнуться с заданием, где нужно примерно оценить значение логарифма – это очень просто! Давайте для примера оценим логарифм \(log_<4>(6)\). Необходимо подобрать слева и справа от 6 такие ближайшие числа, логарифм от которых мы сможем посчитать, другими словами, надо найти степени 4-ки ближайшие к 6ке:
Значит \(log_<4>(6)\) принадлежите промежутку от 1 до 2:
Как посчитать логарифм
Почему так? Это следует из определения показательной функций. Показательная функция не может быть \(0\). А основание не равно \(1\), потому что тогда логарифм теряет смысл – ведь \(1\) в любой степени это будет \(1\).
При этих ограничениях логарифм существует.
В дальнейшем при решении различных логарифмических уравнений и неравенств вам это пригодится для ОДЗ.
Обратите внимание, что само значение логарифма может быть любым. Это же степень, а степень может быть любой – отрицательной, рациональной, иррациональной и т.д.
Теперь давайте разберем общий алгоритм вычисления логарифмов:
Давайте разберем на примерах.
Пример 1. Посчитать логарифм \(9\) по основанию \(3\): \(log_<3>(9)\)
Пример 2. Вычислить логарифм \(\frac<1><125>\) по основанию \(5\): \(log_<5>(\frac<1><125>)\)
Пример 3. Вычислить логарифм \(4\) по основанию \(64\): \(log_<64>(4)\)
Пример 4. Вычислить логарифм \(1\) по основанию \(8\): \(log_<8>(1)\)
Пример 5. Вычислить логарифм \(15\) по основанию \(5\): \(log_<5>(15)\)
Как понять, что некоторое число \(a\) не будет являться степенью другого числа \(b\). Это довольно просто – нужно разложить \(a\) на простые множители.
\(16\) разложили, как произведение четырех двоек, значит \(16\) будет степенью двойки.
Разложив \(48\) на простые множители, видно, что у нас есть два множителя \(2\) и \(3\), значит \(48\) не будет степенью.
Теперь поговорим о наиболее часто встречающихся логарифмах. Для них даже придумали специально названия – десятичный логарифм и натуральный логарифм. Давайте разбираться.
Десятичный логарифм
Натуральный логарифм
Натуральные и десятичные логарифмы подчиняются тем же самым свойствам и правилам, что и обыкновенные логарифмы.
У логарифмов есть несколько свойств, по которым можно проводить преобразования и вычисления. Кроме этих свойств, никаких операций с логарифмами делать нельзя.
Свойства логарифмов
Давайте разберем несколько примеров на свойства логарифмов.
Пример 8. Воспользоваться формулой \(3\). Логарифм от произведения – это сумма логарифмов.
Пример 9. Воспользоваться формулой \(4\). Логарифм от частного – это разность логарифмов.
Пример 10. Формула \(5,6\). Свойства степени.
Логично, что будет выполняться и такое соотношение:
Пример 11. Формулы \(7,8\). Переход к другому основанию.
Логарифм. Как вычислить логарифм?
Логарифмом положительного числа \(c\) по основанию \(a\) \((a>0, a\neq1)\) называется показатель степени \(b\), в которую надо возвести основание \(a\), чтобы получить число \(c\) \((c>0)\), т.е.
Объясним проще. Например, \(\log_<2><8>\) равен степени, в которую надо возвести \(2\), чтоб получить \(8\). Отсюда понятно, что \(\log_<2><8>=3\).
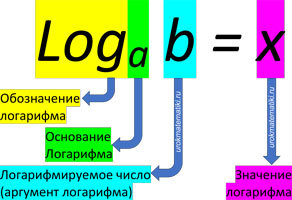
Аргумент и основание логарифма
Любой логарифм имеет следующую «анатомию»:
Как вычислить логарифм?
а) В какую степень надо возвести \(4\), чтобы получить \(16\)? Очевидно во вторую. Поэтому:
в) В какую степень надо возвести \(\sqrt<5>\), чтобы получить \(1\)? А какая степень делает любое число единицей? Ноль, конечно!
г) В какую степень надо возвести \(\sqrt<7>\), чтобы получить \(\sqrt<7>\)? В первую – любое число в первой степени равно самому себе.
В сложных случаях для вычисления логарифма удобно переводить его в показательное уравнение.
Нам надо найти значение логарифма, обозначим его за икс. Теперь воспользуемся определением логарифма:
\(\log_
Слева воспользуемся свойствами степени: \(a^
Основания равны, переходим к равенству показателей
Умножим обе части уравнения на \(\frac<2><5>\)
Получившийся корень и есть значение логарифма
Зачем придумали логарифм?
Чтобы это понять, давайте решим уравнение: \(3^
А теперь решите уравнение: \(3^
Самые догадливые скажут: «икс чуть меньше двух». А как точно записать это число? Для ответа на этот вопрос и придумали логарифм. Благодаря ему, ответ здесь можно записать как \(x=\log_<3><8>\).
\(4^<5x-4>\) и \(10\) никак к одному основанию не привести. Значит тут не обойтись без логарифма.
Воспользуемся определением логарифма:
\(a^=c\) \(\Leftrightarrow\) \(\log_
Зеркально перевернем уравнение, чтобы икс был слева
И не пугайтесь логарифма, относитесь к нему как к обычному числу.
Поделим уравнение на 5
Вот наш корень. Да, выглядит непривычно, но ответ не выбирают.
Десятичный и натуральный логарифмы
Как указано в определении логарифма, его основанием может быть любое положительное число, кроме единицы \((a>0, a\neq1)\). И среди всех возможных оснований есть два встречающихся настолько часто, что для логарифмов с ними придумали особую короткую запись:
Десятичный логарифм: логарифм, у которого основание равно 10, записывается \(\lg\).
Основное логарифмическое тождество
У логарифмов есть множество свойств. Одно из них носит название «Основное логарифмическое тождество» и выглядит вот так:
Это свойство вытекает напрямую из определения. Посмотрим как именно эта формула появилась.
Вспомним краткую запись определения логарифма:
Пример: Найдите значение выражения \(36^<\log_<6><5>>\)
Вот теперь спокойно пользуемся основным логарифмическим тождеством.
Как число записать в виде логарифма?
Как уже было сказано выше – любой логарифм это просто число. Верно и обратное: любое число может быть записано как логарифм. Например, мы знаем, что \(\log_<2><4>\) равен двум. Тогда можно вместо двойки писать \(\log_<2><4>\).
Таким образом, если нам нужно, мы можем где угодно (хоть в уравнении, хоть в выражении, хоть в неравенстве) записывать двойку как логарифм с любым основанием – просто в качестве аргумента пишем основание в квадрате.
Точно также и с тройкой – ее можно записать как \(\log_<2><8>\), или как \(\log_<3><27>\), или как \(\log_<4><64>\)… Здесь мы как аргумент пишем основание в кубе:
Логарифмы
Что такое логарифм?
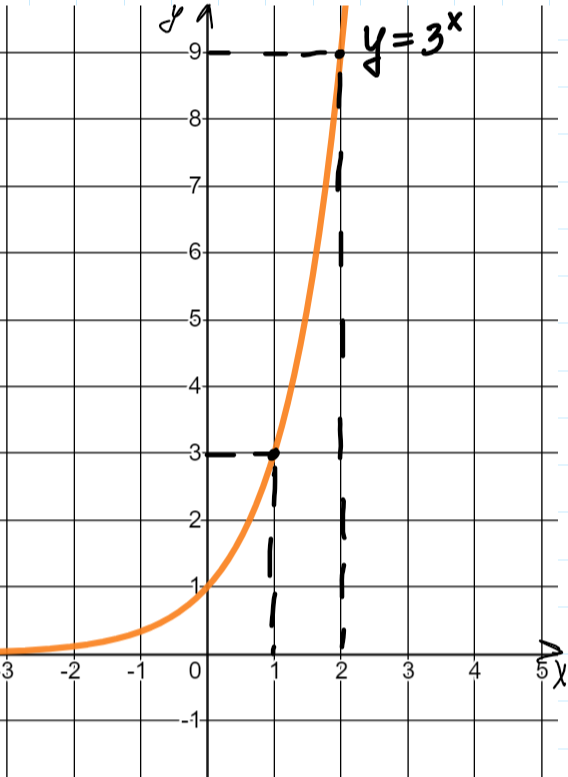
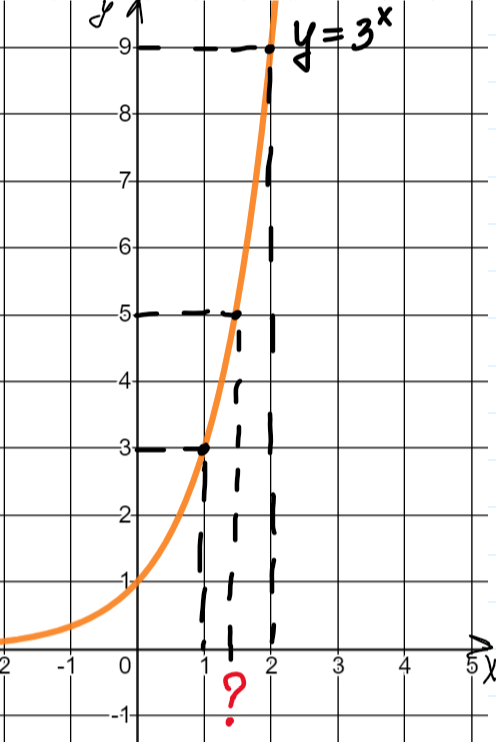
Нагляднее всего понять это с помощью графического решения уравнений. Начертим график и с его помощью решим уравнения:
И в этом случае невозможно назвать точное значение, то есть мы понимаем, что корень больше одного и меньше двух, но более точных данных нет.
Вот такой корень и задается с помощью логарифма, а именно (читается как «логарифм пяти по основанию три» или «логарифм по основанию три от пяти»).
Мы определили смысл — теперь перейдем к общему определению логарифма.
Логарифмом числа b по основанию a называют показатель степени с основанием a, равной b. То есть, попросту говоря, логарифм — это степень, в которую нужно возвести a для получения b. Однако у логарифма есть условия или ограничения, что основание а больше нуля и не равно единице, а также показатель b больше нуля.
Как решать примеры с логарифмами?
Рассмотрим пример, как решить логарифм:
Задаем вопрос: в какую степень нужно возвести 7, чтобы получить 49?
Какие бывают виды логарифмов?
Свойства и формулы логарифмов
Эта формула называется основным логарифмическим тождеством.
Видно, что показатель степени выносим перед логарифмом.
Применение логарифмических свойств в примерах
Пример 1
Решение
У каждого логарифма в показателе стоит степень, значит, поможет 4-я формула:
Первый логарифм можно вычислить по определению. И обратите внимание на второй логарифм: у него в основании стоит а, а в условии задачи дан логарифм с основанием b, значит, нужно а как-то заменить на b. Возможно ли это? Конечно, 7-я формула в помощь!
Подставьте числовое значение из условия, и все готово:
Отличный пример! Мы использовали практически все свойства логарифмов. А теперь попрактикуйтесь еще, но помните, что задача с подвохом!
Пример 2
Получился ответ 27? Если да, то поздравляю: вы попались на удочку самых популярных ошибок! Какое бы задание вам ни встретилось, действия с логарифмами нужно производить только по определениям и правилам. В примере вы видите деление двух логарифмов. А есть ли какая-то формула, в которой записано деление двух логарифмов?
Конечно, это формула перехода к новому основанию, которую мы привели в пункте 6 выше. Применим ее к этому случаю и вычислим логарифм по определению, задав вопрос: в какую степень нужно возвести основание, чтобы получился показатель?
И получается ответ 4, а не 27.
Практическое применение логарифмов
Помните, выше мы говорили, что логарифм объединяет задания на ЕГЭ, галактики и рога горных козлов? И если с баллами на ЕГЭ все понятно, то про галактики и рога — интереснее.
Как видите, логарифмы имеют большое значение для нашей жизни — не только баллы на ЕГЭ!
Вопросы для самопроверки
Чтобы информация точно усвоилась, вспомните:
Что такое логарифм?
Какие ограничения есть у логарифма?
Какие логарифмические свойства вы знаете?
Какие бывают способы преобразования выражений с логарифмом?
В чем практическое применение логарифмов?
На курсах по математике в онлайн-школе Skysmart мы всегда показываем, зачем нужны математические правила и формулы в реальной жизни — ведь так учиться гораздо интереснее! И подтянуть знания перед ЕГЭ тоже поможем: приходите на бесплатный вводный урок и все увидите сами.
Что такое логарифм. Как посчитать логарифм. Свойства логарифмов. Примеры решения логарифмов
Многие школьники считают логарифмы сложной темой в курсе математики. Но если разобрать, что такое логарифм подробно, от простого к сложному, то на ЕГЭ вы не станете их опасаться.
Часто у учеников возникает путаница, где аргумент, а где основание логарифма. И что же нужно возвести в степень, чтобы этот логарифм, наконец, посчитать.
В этой статье мы откроем секрет, как легче запомнить принцип решения логарифма.
Итак, давайте разбираться, что такое логарифм.
Что такое логарифм и как его посчитать
Логарифм имеет следующий вид:

b – это аргумент логарифма
Чтобы узнать значение логарифма приравняем его к X.

Чтобы было легче, можно запоминать так – основание всегда остается внизу (и в первом, и во втором выражении a внизу)!
Чтобы вычислить данный логарифм, необходимо приравнять его к X и воспользоваться правилом, описанным выше:

Логарифмы со специальным обозначением
Для некоторых логарифмов в математике введены специальные обозначения. Это связано с тем, что такие логарифмы встречаются особенно часто. К таким логарифмам относятся десятичный логарифм и натуральный логарифм. Для этих логарифмов справедливы все правила, что и для обычных логарифмов.
Десятичный логарифм
Десятичный логарифм обозначается lg и имеет основание 10, т.е.

Например, вычислим lg100
Натуральный логарифм
Натуральный логарифм обозначается ln и имеет основание e, то есть
Чтобы вычислить данный логарифм нужно число е возвести в степень x. Некоторые из вас спросят, что это за число такое е? Число е – это иррациональное число, т.е. точное его значение вычислить невозможно. е = 2,718281…
Сейчас не будем подробно разбирать, зачем это число нужно, просто запомним, что
И вычислить его можно таким образом:
Основные свойства логарифмов
Логарифмы можно преобразовывать, но для этого необходимо знать правила, которые называются основными свойствами логарифмов. Данные свойства обязательно нужно знать каждому ученику! Без знания этих свойств невозможно решить ни одну серьезную логарифмическую задачу. Вот эти свойства:
Совет – тренируйтесь применять эти свойства в обе стороны, то есть как слева направо, так и справа налево!
Рассмотрим свойства логарифмов на примерах.
Логарифмический ноль и логарифмическая единица
Это следствия из определения логарифма. И их нужно обязательно запомнить. Эти простейшие свойства нередко вводят учеников в ступор.
Запомните, что логарифм от a по основанию а всегда равен единице:
loga a = 1 – это логарифмическая единица.
Если же в аргументе стоит единица, то такой логарифм всегда равен нулю независимо от основания, так как a 0 = 1:
loga 1 = 0 – логарифмический ноль.
Основное логарифмическое тождество
В первой формуле число m становится степенью, которая стоит в аргументе. Данное число может быть любым. Некоторые выражения могут быть решены только с помощью этого тождества.
Вторая формула по сути является просто переформулированным определением логарифма
Разберем применение тождества на примере:
Необходимо найти значение выражения


Сумма логарифмов. Разница логарифмов
Логарифмы с одинаковыми основаниями можно складывать:

Обратите внимание, что формулы суммы и разности логарифмов верны только для логарифмов с одинаковыми основаниями! Если основания разные, то данные свойства применять нельзя!
Вынесение показателя степени из логарифма
Вынесение показателя степени из логарифма:
Переход к новому основанию

Такие формулы чаще всего нужны при решении логарифмических уравнений и неравенств.
Разберем на примере.
Необходимо найти значение такого выражения
Теперь применим переход к новому основанию для второго логарифма:
10 примеров логарифмов с решением
1. Найти значение выражения















10. Найти значение выражения
Надеюсь, теперь вы разобрались, что такое логарифм.
Свойства логарифмов и примеры их решений
Зачем в жизни нужны логарифмы?
Я уже говорил, что математики СУПЕРленивые люди? Это правда.
Вот представь себе, им лень умножать и они придумали логарифмы, которые позволяют заменить умножение сложением!
Им еще больше лень возводить в степень и они используют логарифмы, чтобы заменить возведение в степень умножением или делением!
То есть они используют логарифмы, чтобы быстро проделывать громоздкие вычисления.
Логарифм и его свойства. Вебинар (1 час 48 минут)
В этом видео мы разобрали свойства логарифмов на примере решения 35 задач.
Начиная от самых простых логарифмов и заканчивая сложными.
Если вам понравилось видео, подписывайтесь на канал, ставьте лайки — нам будет приятно и мы будем делать такие видео впредь.
Что такое логарифм?
Для начинающих объясним все человеческим языком. Логарифмы – очень простая тема.
Чтобы понять, как их решать, нужно всего лишь разобраться, что как называется, знать таблицу умножения и уметь возводить в число в степень.
Все. Больше ничего не нужно.
Начнем с простого. Как решить уравнение \(\displaystyle <<2>^
Очень легко – просто ответь на вопрос в какую степень нужно возвести число \(2\) чтобы получить \(8\)?
Решаем методом подбора: два в первой степени – нет, два во второй степени – нет, два в третей степени – ДА!
Двойку нужно возвести в ТРЕТЬЮ степень, чтобы получить восемь (\(\displaystyle <<2>^<3>>=8\)) и значит решением уравнения будет число три (\(x=3\)).
Следующий вопрос. Как решить уравнение \(\displaystyle <<2>^
Опять просто ответь на вопрос в какую степень нужно возвести число \(2\), чтобы получить число \(5\)?
Попытаемся подобрать: два во второй степени равно четыре – мало, два в третьей степени равно восемь – много.
Метод подбора сразу ответ не дает… Да и вообще, в этом случае подобрать решение не получится – ведь это не только нецелое число, это число даже не рациональное.
Для нахождения таких решений было придумано понятие логарифм:
В общем виде он записывается так:
То есть логарифм – это степень, в которую нужно возвести основание, чтобы получить аргумент.
Если ты посчитаешь на калькуляторе, то получишь \(2,321928\ldots \) и т.д. Это число иррациональное. Оно мало того, что не подбирается, оно еще и не кончается…
Ну и как с такими числами работать? Как их запоминать? Как их записывать?
В нашем случае решение уравнения можно записать как \(2,321928\ldots \) или как \(\displaystyle <<\log >_<2>>5\).
Согласись второе выражение гораздо удобнее, чем первое. И оно, кстати, абсолютно точное. Словами это произносится как:
Решением уравнения два в степени икс равно пяти является логарифм пяти по основанию два, или логарифм по основанию два от пяти.
Кстати, а ты заметил что и у степени числа и у логарифма основание всегда находится «ВНИЗУ». Легко запомнить правда? А вот «вверху», у степени находится ее показатель, а у логарифма – аргумент.
Выражение \(\displaystyle <<2>^<3>>=8\) можно также записать в виде \(\displaystyle <<\log >_<2>>8=3\). Читается так:
«Логарифм восьми по основанию два равен трем»
«Логарифм по основанию два от восьми равен трем»
Теперь более общая запись:
«Чтобы получить число \(b\), нужно число \(a\) возвести в степень \(c\)»:
8 примеров вычисления логарифмов
Пример 1
Чему равен \(\displaystyle <<\log >_<2>>4\)?
\(\displaystyle <<\log >_<2>>4=2\), так как число \(2\) нужно возвести во вторую степень, чтобы получить \(4\).
Пример 2
Чему равен \(\displaystyle <<\log >_<2>>\frac<1><8>\)?
Заметим, что \(\displaystyle 8=<<2>^<3>>\), тогда \(\displaystyle \frac<1><8>=\frac<1><<<2>^<3>>>=<<2>^<-3>>\), то есть \(2\) нужно возвести в степень \(-3\), чтобы получить \(\displaystyle \frac<1><8>\).
Пример 3
А чему равен \(\displaystyle <<\log >_<2>>0,25\)?
Обращать внимание нужно, в первую очередь, на основание. Возможно ли представить \(0,25\) как \(2\) в какой-то степени? Да, возможно: запишем это число в виде обычной дроби: \(\displaystyle 0,25=\frac<1><4>=\frac<1><<<2>^<2>>>=<<2>^<-2>>\).
Пример 4
Чему равен \(\displaystyle <<\log >_<7>>1\)?
В какую степень надо возвести \(7\), чтобы получить \(1\)? Вспоминаем, что любое число в нулевой степени равно \(1\) (подробнее читай в разделе «Степень и ее свойства»).
Значит, \(\displaystyle <<\log >_<7>>1=0\). Более того, логарифм с любым основанием от единицы равен \(0\).
Пример 5
\(\displaystyle <<\log >_<4>>2\). В этом случае аргумент \(2\) равен корню основания: \(\displaystyle 2=\sqrt<4>\).
Но мы помним, что корень тоже можно представить в виде степени (с дробным показателем): \(\displaystyle 2=\sqrt<4>=<<4>^<\frac<1><2>>>\text< >\Rightarrow \text< ><<\log >_<4>>2=\frac<1><2>\).
Попробуй найти следующие 4 логарифма самостоятельно
Десятичные логарифмы
Логарифм по основанию \(\displaystyle 10\) называется десятичным логарифмом и записывается упрощенно: \(\displaystyle \lg \) вместо \(\displaystyle <<\log >_<10>>\)
Когда нужная степень не подбирается
Как я уже говорил, далеко не всегда удается подобрать такую степень. Но это не значит, что такого числа не существует, просто его можно вычислить только на калькуляторе.
Например, \(\displaystyle <<\log >_<2>>5=2,321928…\).
Видим, что это число расположено между \(\displaystyle 2\) и \(\displaystyle 3\), и это понятно: ведь это значит, чтобы получить \(5\), нужно \(2\) возводить в степень больше \(2\), но меньше \(3\).
На ЕГЭ пользоваться калькулятором нельзя, но даже если бы было можно, нельзя записывать приближенные вычисления.
Поэтому, если перед нами задача первой части, ответ обязательно должен получиться «хороший», и его можно посчитать в уме.
В письменной части могут попасться и «плохие» числа; в этом случае пугаться не нужно, в ответе можно просто написать логарифм.
Например, ответ вполне может выглядеть так:
\(\displaystyle <<\log >_<3>>10\), или даже так: \(\displaystyle \frac<2+<<\log >_<3>>7><5>\).
Получается, что теперь мы можем мгновенно записать решение любого элементарного показательного уравнения:
Но увлекаться и халтурить тоже не стоит – если в ответе оставить \(\displaystyle x=<<\log >_<3>>81\), высший балл за задачу не поставят.
То есть, если ответ возможно упростить и представить в виде рационального числа, это обязательно нужно будет сделать.
Потренируйся на следующих простых примерах:
6 примеров для самостоятельной работы
Ответы:
Открыть ответы…
Чтобы открыть все задачи учебника, закрытые голубыми баннерами (как этот), зарегистрируйтесь один раз:
Область допустимых значений (ОДЗ)логарифма
Мы помним, что, например, квадратный корень нельзя извлекать из отрицательных чисел; или если у нас дробь, то знаменатель не может быть равен нулю. Подобные ограничения есть и у логарифмов:
То есть и аргумент, и основание должны быть больше нуля, а основание еще и не может равняться \( 1\).
Начнем с простого: допустим, что \( a=1\). Тогда, например, число не существует, так как в какую бы степень мы не возводили \( 1\), всегда получается \( 1\).
Более того, \( \displaystyle <<\log >_<1>>b\) не существует ни для какого \( \displaystyle b\ne 1\).
Но при этом \( \displaystyle <<\log >_<1>>1\) может равняться чему угодно (по той же причине – \( 1\) в любой степени равно \( 1\)).
Поэтому объект не представляет никакого интереса, и его просто выбросили из математики.
Похожая проблема у нас и в случае \( a=0\): \( 0\) в любой положительной степени – это \( 0\), а в отрицательную его вообще нельзя возводить, так как получится деление на ноль (напомню, что \( \displaystyle <^<-c>>=\frac<1><<^
При \( a 0\\x\ne 1\\x+2>0\end
Пример 1 (попробуй решить самостоятельно)
Найдите корень уравнения \( \displaystyle <<\log >_
Решение:
\( \displaystyle <<\log >_
Открыть ответы…
Чтобы открыть все задачи учебника, закрытые голубыми баннерами (как этот), зарегистрируйтесь один раз:
Основное логарифмическое тождество
Вспомним определение логарифма в общем виде:
Подставим во второе равенство вместо \( \displaystyle c\) логарифм:
Это равенство называется основным логарифмическим тождеством. Хотя по сути это равенство – просто по-другому записанное определение логарифма:
Реши еще следующие примеры:
Пример 2
Найдите значение выражения \( \displaystyle <<25>^<<<\log >_<5>>3>>\).
Пример 3
Решения примеров 2 и 3:
Открыть ответы…
Чтобы открыть все задачи учебника, закрытые голубыми баннерами (как этот), зарегистрируйтесь один раз:
Свойства логарифмов
К сожалению, задачи не всегда такие простые – зачастую сперва нужно упростить выражение, привести его к привычному виду, и только потом будет возможно посчитать значение.
Это проще всего сделать, зная свойства логарифмов.
Так что давай выучим основные свойства логарифмов. Каждое из них я буду доказывать, ведь любое правило проще запомнить, если знать, откуда оно берется.
Все эти свойства нужно обязательно запомнить, без них большинство задач с логарифмами решить не получится.
А теперь обо всех свойствах логарифмов подробнее.
Свойство 1 – степень аргумента
Доказательство:
Свойство 2 – сумма логарифмов
Сумма логарифмов с одинаковыми основаниями равна логарифму произведения: \( \displaystyle <<\log >_>b+<<\log >_>c=<<\log >_>\left( b\cdot c \right)\).
Доказательство:
Пример
Найдите значение выражения: \( \displaystyle <<\log >_<3>>5+<<\log >_<3>>0,6\).
Решение:
Открыть ответы…
Мы постоянно улучшаем этот учебник и вы можете нам в этом помочь.
Оформите доступ и пользуйтесь учебником ЮКлэва без ограничений (100+ статей по всем темам ОГЭ и ЕГЭ, 2000+ разобранных задач, 20+ вебинаров-практикумов)
А вот обещанное упрощение:
Зачем это нужно? Ну например: чему равно \( \displaystyle lo<
Теперь упрости сам:
Ответы:
Открыть ответы…
Мы постоянно улучшаем этот учебник и вы можете нам в этом помочь.
Оформите доступ и пользуйтесь учебником ЮКлэва без ограничений (100+ статей по всем темам ОГЭ и ЕГЭ, 2000+ разобранных задач, 20+ вебинаров-практикумов)
Свойство 3 – разность логарифмов
| Разность логарифмов с одинаковыми основаниями равна логарифму частного:\( \displaystyle lo< |
Доказательство:
Все точно так же, как и в пункте 2:
Пример из прошлого пункта теперь становится еще проще:
Пример посложнее: \( \displaystyle \log _<2>^<2>2\sqrt<3>-\log _<2>^<2>\sqrt<3>—<<\log >_<2>>3\).
Догадаешься сам, как решить?
Здесь нужно заметить, что у нас нету ни одной формулы про логарифмы в квадрате. Это что-то сродни выражению \( \displaystyle <<2>^<<
Поэтому отвлечемся от формул про логарифмы, и подумаем, какие вообще формулы мы используем в математике чаще всего? Еще начиная с 7 класса!
Это – формулы сокращенного умножения. Нужно привыкнуть к тому, что они везде! И в показательных, и в тригонометрических, и в иррациональных задачах они встречаются. Поэтому их нужно обязательно помнить.
Нажми на ссылку «Формулы сокращенного умножения», и внимательно на них посмотри. Какую из них можно применить здесь?
Если присмотреться к первым двум слагаемым, становится ясно, что это разность квадратов:
Дальше все просто – применяем только что выученные правила 2 и 3. Что получилось?
Ответ для проверки:
Упрости сам:
Ответы:
Открыть ответы…
Мы постоянно улучшаем этот учебник и вы можете нам в этом помочь.
Оформите доступ и пользуйтесь учебником ЮКлэва без ограничений (100+ статей по всем темам ОГЭ и ЕГЭ, 2000+ разобранных задач, 20+ вебинаров-практикумов)
Свойство 4 – вынесение показателя степени из аргумента логарифма
Если в аргументе логарифма стоит степень, показатель этой степени можно вынести за знак логарифма: \( \displaystyle <<\log >_><^
>=n\cdot <<\log >_>b\)
Доказательство:
Можно понять это правило так:
То есть степень аргумента выносится вперед логарифма, как коэффициент.
Пример: Найдите значение выражения \( \displaystyle \frac<<<\log >_<2>>25><<<\log >_<2>>5>\).
Реши сам:
Ответы:
Открыть ответы…
Мы постоянно улучшаем этот учебник и вы можете нам в этом помочь.
Оформите доступ и пользуйтесь учебником ЮКлэва без ограничений (100+ статей по всем темам ОГЭ и ЕГЭ, 2000+ разобранных задач, 20+ вебинаров-практикумов)
Свойство 5 – вынесение показателя степени из основания логарифма
Доказательство:
Запоминаем: из основания степень выносится как обратное число, в отличии от предыдущего случая!
Свойство 6 – вынесение показателя степени из основания и аргумента логарифма
Если в основании и аргументе логарифма стоят степени, показатели этих степеней можно вынести за знак логарифма: \( \displaystyle <<\log >_<<^
>>><^ >=\frac \cdot <<\log >_>b\).
Свойство 7 – переход к новому основанию
Если основания логарифмов разные, то для того чтобы дальше работать с логарифмами нужно перейти к логарифмам с одним основанием: \( \displaystyle <<\log >_>b=\frac<<<\log >_
>b><<<\log >_ >a>\text< >\left( c>0;\text< >\ne \text <1>\right)\).
Доказательство:
Свойство 8 – замена местами основания и аргумента логарифма
Можно менять местами основание и аргумент логарифма, но при этом все выражение «переворачивается», т.е. логарифм оказывается в знаменателе: \( \displaystyle <<\log >_>b=\frac<1><<<\log >_>a>,\text< >\left( b\ne 1 \right)\).
Доказательство:
Рассмотрим еще несколько примеров.
Пример 1. Найдите значение выражения \( \displaystyle <<\log >_<5>>75+<<\log >_<5>>\frac<1><3>\).
Пример 2. Найдите значение выражения \( \displaystyle <<\log >_<3>>36-2<<\log >_<3>>2\).
Пример 3. Найдите значение выражения \( \displaystyle <<\log >_<8\sqrt[5]<4>>>\left( 32\sqrt[5] <2>\right)\).
Пример 4. Найдите значение выражения \( \displaystyle \frac<\log _<5>^<2>25\sqrt<10>-\log _<5>^<2>\sqrt<10>><<<\log >_<5>>250>.\).
Открыть ответы…
Мы постоянно улучшаем этот учебник и вы можете нам в этом помочь.
Оформите доступ и пользуйтесь учебником ЮКлэва без ограничений (100+ статей по всем темам ОГЭ и ЕГЭ, 2000+ разобранных задач, 20+ вебинаров-практикумов)
Самые бюджетные курсы по подготовке к ЕГЭ на 90+
Алексей Шевчук — ведущий курсов
Добавить комментарий Отменить ответ
21 комментарий
Отличный материал! Спасибо!
Спасибо, Саид. В каком вы классе?
Вы — это просто чу-до, и этот учебник тоже! Если бы я знала о вас в сентябре, я бы выбрала вашу онлайн школу
Спасибо большое, Бася! Очень приятно слышать. Желаем вам сдать ЕГЭ на 100 баллов! )
Как лайк поставить?
Будем считать этот коммент лайком. Спасибо!
хотела зарегистрироваться на вебинар 14 февраля, но не смогла: «сайт не может обеспечить безопасное соединение» может есть еще вариант?
Надежда, я зарегистрировал вас и отправил на почту доступы. Скажите, пожалуйста, где вы столкнулись с такой надписью? Можете написать или отправить ссылку?
Большое спасибо, все изложено четко и красиво!
Инна, очень рады, что понравилось! Заходите к нам еще! )
Это лучшее объяснение, что я встречала! Хорошая методика: простой язык, примеры и практика! Я благодарна Клеверу!
Спасибо, Ника! И за название тоже. «Клевер» — клёво! ))
Некоторые комментарии прошлых лет к этой статье:
Катерина
10 января 2018
Я получила очень хорошую для меня информацию.
Александр (Админ)
11 января 2018
Спасибо, Катерина. Нам очень приятно слышать, что наш учебник полезен.
Владимир
17 января 2018
Прекрасное объяснение! Просто великолепное! В примере после третьего свойства действительно есть опечатка. знак корня у третьего члена лишний. Есть также потерянный член в конце предпоследней строчки решения пятой задачи третьего свойства. В финальной строчке он нашелся 🙂
Алексей Шевчук
06 февраля 2018
Александр, примени свойство степени «произведение степеней с одинаковым основанием»: https://youclever.org/book/stepen-i-ee-svojstva
Дарья
10 декабря 2018
А как решать функцию логарифмическую, если логарифм под знаком модуля? Например y=[lgx]-lgx?
Шура
24 января 2019
Как сложить логарифмы если у обоих аргумент x, но у первого основание 2, а у второго 3?
Алексей Шевчук
04 февраля 2019
Шура, нужно воспользоваться формулой перехода к другому основанию Например, log_3 (x) = log_2 (x) / log_2 (3).
Олег
14 апреля 2019
Большое спасибо за очередную великолепную статью, все понятно.
Александр (админ)
14 апреля 2019
Олег, очень рады слышать! Удачи!
Олег
17 апреля 2019
Спасибо за статью, но СЛОЖНА
Александр (админ)
17 апреля 2019
Пожалуйста, Олег. Ну что поделать? Тяжело в ученье, легко на ЕГЭ )
Саня
06 сентября 2019
А что делать, если логарифмы с разными приколами? 0-0 Как их решать?
Алексей Шевчук
06 сентября 2019
Саня, посмотри статью про логарифмические уравнения, там некоторые приколы разобраны. https://youclever.org/book/logarifmicheskie-uravneniya-1
Алексей Шевчук
08 ноября 2019
Виталий, дело в том, что такие уравнения будут иметь действительные решения очень редко. Представим себе, что это уравнение (-2)^6x=-8. Тогда с одной стороны, x=0.5 является решением, но с другой стороны, когда мы решаем уравнение, у нас должна быть возможность воспользоваться свойствами степени: (-2)^6x = ((-2)^x)^6 — а теперь посмотрим, можем ли мы так делать? Подставим вместо x число 0.5: ((-2)^0.5)^6=-8. Вспомним, что такое степень 0.5? Это квадратный корень из числа. Но ведь мы не можем извлекать корень из отрицательного числа! Чтобы не возникало таких неприятностей, математики договорились не использовать отрицательные основания у показательной функции, а как следствие, и у логарифма. Но это касается только вычислений в действительных числах. Если мы рассматриваем также комплексные числа (это в которых можно извлекать корень из отрицательных чисел), то отрицательные основания возможны — но это уже не школьная математика.
Александр (админ)
08 ноября 2019
Отличное объяснение, Алексей! Снова вышли за пределы школьной математики. Это здорово! )
Виталий
12 ноября 2019
Спасибо за ответ. Понял, что это для облегчения начальной стадия обучения, с последующим переходом к более сложным вычислениям.
Антон
16 декабря 2019
Классное объяснение, спасибо!
Александр (админ)
16 декабря 2019
Антон, спасибо! Мы рады, что понравилось. Заходи еще! )
Света
07 января 2020
Спасибо очень понравилась то что не было не понятно все поняла
Александр (админ)
07 января 2020
Отлично, Света! Мы очень рады. Удачи тебе на экзаменах!
Александр (админ)
13 января 2020
То, что не нравится Полине Магаррамовой я переживу как-нибудь. Мне главное, чтобы вам нравилось 🙂
Евгений Вячеславович
06 февраля 2020
Классно… Если бы мне 19 лет назад так объясняли бы математику, я бы к егэ вообще не готовился бы, потому что все бы помнил и понимал. Так доходчиво и понятно я не встречал нигде. Спасибо вам.
Александр (админ)
06 февраля 2020
Спасибо, Евгений Вячеславович. Я вот тоже самое думаю, что, если бы мне объясняли также как здесь в свое время…. ))
Юлия Владимировна
13 мая 2020
Помогите решить: 2*log 1/2 (4x-5) — log1/2 *16x = log1/2(x-3)
Алексей Шевчук
14 мая 2020
Юлия Владимировна, двойку вносим в логарифм как степень аргумента: 2*log 1/2 (4x-5)=log 1/2 (4x-5)^2. Потом соединяем логарифмы по правилу вычитания: log 1/2 [(4x-5)^2 / 16x] = log1/2(x-3). Теперь можно от логарифмов избавиться: (4x-5)^2 /16x = (x-3) — получили обычное уравнение
Жахиян
27 мая 2020
В какую степень нужно возвести число 2 чтобы получить 8? как ответ может быть 3. По идей ответ дожен быть равно на 4 а не к 3.
Александр (админ)
27 мая 2020
Жахиян, вы говорите на какое число нужно УМНОЖИТЬ 2, чтобы получить 8. Это действительно 4. Но вопрос был В КАКУЮ СТЕПЕНЬ нужно возвести 2 чтобы получить 8. А это тройка: «два в третьей степени будет восемь» (2*2*2=8)
ООО,спасибо за последние слова,лучший сайт.
Преобразование выражений с использованием свойств логарифмов: примеры, решения
Если у нас есть выражение, содержащее логарифмы, то мы можем преобразовать его с учетом свойств этих логарифмов. В этом материале мы рассмотрим основные правила, по которым осуществляется данное преобразование.
В первом пункте приведем основные свойства логарифмов, представив их в виде списка. Далее рассмотрим характерные примеры преобразований с использованием этих свойств. Отдельно остановимся на числовых выражениях и на выражениях с переменными, а также посмотрим, как преобразовывать примеры с использованием модуля.
Свойства логарифмов
log a q b p = log a b p log a a q = p · log a b q = p q · log a b
То же относится и к последнему свойству из списка, выраженному формулой b log a c = C log a c = c log a b : оно тоже может быть выведено из основных свойств. Нужно учитывать, что если у нас есть степень положительного числа с логарифмом в показателе, то мы всегда можем поменять число под логарифмом и основание степени местами. В принципе, на практике такие задачи встречаются не слишком часто, но мы их все же разберем.
Как преобразовать числовое выражение с логарифмом
После того, как мы вспомнили основные свойства логарифмов, покажем, как использовать их при решении задач. Начнем с того, как преобразовывать числовые выражения, потому что такие вычисления считаются более простыми. Возьмем сперва примитивные примеры, с помощью которых легко проиллюстрировать выбор нужного свойства логарифма, а потом будем наращивать сложность задач. В конце разберем задания, в которых нужно использовать сразу несколько свойств.
Как выбрать свойство логарифма для преобразования
Список свойств, приведенный в первом пункте, довольно большой, и очевидно, что нужно хорошо в нем ориентироваться, чтобы получить нужный результат. Обычно выбор делается по итогам сравнения исходного логарифма/выражения с левыми и правыми частями формул, выражающих свойства. В том случае, когда одна из частей формулы похожа на исходный логарифм или выражение, мы берем именно это свойство и выполняем преобразование с его помощью. Покажем на примерах, как именно это делается.
Решение
Далее возьмем примеры с другими свойствами логарифмов.
Решение
Решение
Решение
Решение
Решение
Решение
Решение
Воспользуемся формулой перехода к новому основанию и представим исходный логарифм как отношение десятичных логарифмов с известными нам значениями.
log 2 5 = l g 5 l g 2
Считаем: ln 11 ln 3 = log 3 11
Мы разобрали множество примеров, где для осуществления преобразования достаточно применить одну формулу свойства логарифма или его определение. Теперь мы можем перейти к более сложным задачам, в которых нужно последовательно применять несколько свойств, а также делать дополнительные преобразования. Однако перед этим запишем еще один важный пример использования следствий из основных свойств логарифмов.
Решение
Задачи с применением нескольких свойств логарифмов
В действительности чаще встречаются более сложные задания, чем те, что мы разобрали в предыдущем параграфе. В них приходится выполнять преобразования в несколько шагов, применяя последовательно одно свойство за другим. Кроме того, они зачастую включают в себя необходимость раскрывать скобки, приводить подобные слагаемые, сокращать обыкновенные дроби и др. Это не так сложно, как кажется, главное – соблюдать правильную последовательность действий.
Решение
Вот все решение без комментариев:
( log 3 15 − log 3 5 ) · 7 log 7 5 = log 3 ( 15 : 5 ) · 5 = = log 3 3 · 5 = 1 · 5 = 5
Решение
Решение
Предварительное преобразование перед применением основных свойств логарифмов
На практике мы часто можем встретить логарифмы, которые внешне не похожи ни на одну часть формулы свойства. Однако при этом преобразование требует применения именно этих формул. Это возможно, если перед этим привести их к соответствующему виду. Это процесс называется тождественным преобразованием.
В роли таких действий могут выступать почти любые преобразования выражений, в том числе раскрытие скобок, вынесение за скобки множителей, применение формул тригонометрии и т.д. Это очевидно, поскольку выражения под знаком логарифма могут содержать практически все, что угодно: модули, скобки, дроби, степени и др. Поэтому нужно уметь выполнять разные виды преобразований, чтобы успешно решать такие задачи.
Данная статья не имеет целью осветить все возможные случаи преобразований, поскольку их очень много. Мы выбрали только четыре, которые наиболее распространены.
Разберем подробно каждый вид преобразования.
Как выделить степень в основании логарифма и под его знаком
Этот пример иллюстрирует нам следующую мысль: если есть возможность, нужно выделить степень в основании и под знаком логарифма, чтобы впоследствии применить свойство логарифма степени. Ниже мы приведем некоторые советы, как именно выделять степени в таких примерах.
Решение
Если исходного числа нет в таблице степеней, то мы можем разложить его на простые множители.
Решение
Выполняем разложение 648 на простые множители.
648 324 162 81 9 3 1 2 2 2 3 3 3
Теперь мы можем преобразовать исходный логарифм произведения в сумму, а потом воспользоваться формулой логарифма степени.
Упрощаем выражение через раскрытие скобок:
Решение
Преобразования, которые нужно сделать, чтобы получить под знаком логарифма нужную степень, могут значительно отличаться от примера к примеру.
Решение
Первое, что нам нужно сделать, – это избавиться от иррациональности в знаменателе первой дроби, лежащей в основании логарифма:
Мы получили результат, схожий с дробью под знаком логарифма. Применим к нему свойства степеней и получим:
Чтобы преобразовать второе выражение, надо воспользоваться тригонометрическими формулами, а конкретно формулой понижения степени cos 2 a = 1 + cos 2 a 2 :
log 2 · cos 1 ( 1 + cos 2 ) 3 = log 2 · cos 1 ( 2 · cos 2 1 ) 3
Как применять свойства степени при преобразовании выражений с логарифмами
Ранее мы уже использовали свойства степеней, чтобы преобразовать выражения под знаком логарифма и его основание. Посмотрим, в каких еще характерных случаях потребуется такая подготовка.
Решение
3 − 2 · 3 log 3 7 = ( 1 9 ) · 7 = 7 9
Посмотрим пример решения такой задачи.
Решение
Вот запись всего решения:
2 log 2 2 3 − 3 log 2 3 = 2 log 2 3 · log 2 3 − 3 log 2 3 = = ( 2 log 2 3 ) log 2 3 − 3 log 2 3 = 3 log 2 3 − 3 log 2 3 = 0
Также встречаются примеры, где предварительная подготовка к использованию свойств логарифмов заключается в применении и свойства умножения степеней с одинаковыми основаниями, и свойства степени в степени. Например,
Преобразование логарифмов с десятичными дробями
В целом можно сказать, что в случае наличия десятичной дроби под знаком логарифма необходимо выполнить переход к обыкновенной дроби. Это поможет увидеть возможности использования свойств логарифмов.
Разберем подобную задачу.
Решение
Начнем с перехода от десятичных дробей к обыкновенным.
Теперь видно, что мы можем преобразовать 25 4 в виде ( 2 5 ) − 2 и воспользоваться формулой логарифма степени. Вычисляем значение:
Преобразование выражений с отрицательными числами под знаком логарифма
( − 2 ) 6 = ( ( − 1 ) · 2 ) 6 = ( − 1 ) 6 · 2 6 = 1 · 2 6 = 2 6
Решение
Сначала заключим, что данное выражение имеет смысл. Воспользоваться сразу свойством логарифма частного у нас нет возможности из-за отрицательных чисел под знаком логарифма, поэтому выполним преобразования.
Как преобразовать логарифмическое выражение с переменными
В предыдущих параграфах мы разобрали, как работать с числовыми выражениями, содержащими логарифмы. Однако если требуется решить логарифмическое неравенство или уравнение, нам понадобится умение работать с теми случаями, когда под знаком логарифма содержится выражение с переменными. В целом при этом мы руководствуемся теми же принципами, что и с числовыми выражениями, но тут следует отдельно пояснить некоторые нюансы, незнание которых ведет к ошибкам.
Особенности преобразований выражений с переменными
Основная трудность состоит в том, что при работе с такими выражениями числа, расположенные под знаком логарифма и в его основании, должны соответствовать особым условиям, а в случае определенных переменных из области допустимых значений эти условия могут оказаться невыполненными. Приведем один наглядный пример.
Почему надо учитывать область допустимых значений
Важно следить, как меняется область значений во время каждого преобразования. Если на каком-либо этапе происходит ее сужение, это повод тщательно проверить все вычисления и определить, правомерно ли использования данного преобразования.
Чаще всего при решении задач приходится иметь дело с выражениями, область допустимых значений которых не ограничивает применение свойств логарифмов в прямом и обратном порядке, но не следует относиться так ко всем примерам. Нужно всегда проверять, что происходит с областью допустимых значений, и своевременно отслеживать возможные ошибки.
Запишем, в ходе каких преобразований чаще всего происходит непреднамеренное сужение области значений:
Теперь, когда мы обговорили тонкости, на которые нужно обращать внимание при преобразовании выражений с переменными с использованием свойств логарифмов, остается разобраться, как правильно эти преобразования проводить.
Правила проведения преобразований
Мы говорили ранее, что чаще всего область допустимых значений позволяет нам применять свойства логарифмов в привычных формулировках.
Решение
На первый взгляд данное выражение нужно преобразовать, используя логарифм степени, то есть сначала вынести нужную степень в виде коэффициента и потом привести подобные слагаемые. Давайте разберемся, правомерно ли применение выбранного свойства в этом случае.
3 · l g ( x + 2 ) 7 − l g ( x + 2 ) − 5 · l g ( x + 2 ) 4 = = 3 · 7 · l g ( x + 2 ) − l g ( x + 2 ) − 5 · 4 · l g ( x + 2 ) = = 21 · l g ( x + 2 ) − l g ( x + 2 ) − 20 · l g ( x + 2 ) = = ( 21 − 1 − 20 ) · l g ( x + 2 ) = 0
Область допустимых значений позволяет нам использовать и другой вариант вычисления, например, такой:
А как быть в случае, если в области допустимых значений нужные условия не будут выполняться? Возьмем соответствующий пример и разберем его.
Решение
Возьмем еще один пример, чтобы закрепить навыки работы с модулями.
Решение
Вычисляем область допустимых значений данного выражения:
А на интервале от одного до двух значение x − 1 будет положительным, а x − 2 и x − 3 – отрицательными. Значит, отрицательные значения нам нужно заключить в знаки модуля. У нас получится, что:
Теперь объединяем получившиеся результаты.
С помощью таких рассуждений и свойств логарифмов отношения, произведения и степени можно вывести несколько результатов, полезных на практике и удобных в использовании:
Решение
На первый взгляд, мы должны взять формулы логарифмов разности, суммы и степени. Давайте посмотрим, насколько правомерно их использование в данном случае. Для начала вычислим область допустимых значений:
Теперь мы можем свободно применить формулу логарифма степени и выполнить приведение подобных слагаемых:
Возможны и другие преобразования, которые дают тот же результат:
Формулы и свойства логарифмов
Определение логарифма
Логарифм — это математическая функция, основанная на свойствах возведения в степень.
Основываясь на математических формулах логарифмов, можно вычислить постоянную константу, которая в корреляции со всеми математическими константами окажет влияние на конечный результат логарифма числа. В месте с тем, этот результат приведет к трансформации объектов, равных пропорции необходимых логарифмов в пересчете на множители обратных функций.
С первого взгляда это сложно понять, но если увеличить коэффициент логарифма на равный ему множитель, то получится свойство логарифма применимое к школьной программе старших классов, а также для учащихся высших учебных заведений.
Категорическое решение логарифмов, основываясь на из свойствах, ставит в пропорцию их виды. Таким образом, формулы логарифмов соотносятся к самим логарифмам, как необходимая часть их самих.
Виды логарифмов
Для определения основания логарифма необходимо сначала определить его вид и, исходя из полученных результатов, по формуле и таблице сравнить корректность полученных значений. Это и будет основанием логарифма.
Чтобы решить логарифм необходимо понять, что a в степени x будет равно b, т.е. в какую степень x необходимо возвести основание логарифма a, чтобы получить значение b.
Примеры логарифмов:
В данных примерах можно увидель сложные и простые логарифмы, решение которых показывает, что всякий тождественный логарифм находится в пропорции его основания, за исключением вводных данных.
Конечно, основание логарифма пропорционально его значению, что приводит к равенству обратного значения. Это также необходимо учесть при рассмотрении равенства, кроме случаев, когда логарифм переностися с левой части равенства в правую.
log 2 8 = 3 (логарифм 8 по основанию 2 ), так как 2 3 = 8
log 7 49 = 2 (логарифм 49 по основанию 7 ), так как 7 2 = 49
Десятичный логарифм
Десятичный логарифм — логарифм по основанию 10.
Десятичный логарифм может быть не только как равенство степеней, но и показывать их различия. Наиболее хорошо это видно при разложении логарифма на члены в качестве констант a и b.
Конечным результатом решения десятичного логарифма является его сходство с натуральным логарифмом.
Примеры десятичных логарифмов:
lg 100 = 2 — десятичный логарифм обозначается именно так (lg), это десятичный логарифм ста;
Натуральный логарифм
При решении натурального логарифма его основа будет схожей с десятичным логарифмом за исключением того, что вместо числа 10 будет использоваться постоянная константа e.
Ещё одной особенностью натурального логарифма будет его неравенство по отношению к обратной функции.
Но стоит не приравнивать такое основание логарифма к прямой константе из-за большой разности при выборе метода подсчета логарифма.
Формулы и свойства логарифмов
Именно это свойство логарифмов позволяет вычислять точные значения в отличае от других методов вычисления.
Неточность других методов вычисления основывается на неверной корреляции остаточного члена логарифмического равенства.
Наряду с этим каждое из свойств является индивидуальным, равно как каждый из его членов. Всё это позволяет сделать вывод, что благодаря формулам, выведенным математиком, вычисления становятся простыми в рамках неравенств.
Основное логарифмическое тождество
Логарифм единицы
Вычисления такого логарифма применяются в балистике при расчете траектории движения объекта, находящегося в непосредственной близости от Земли. Это обусловлено наиболее точным значением ускорением свободного падения, равным 9,81. А при удалении от поверности Земли это значение изменяется, уменьшается пропорционально расстоянию удаления от поверхности.
Логарифм числа, равного основанию
Логарифмическая единица. Если аргумент и основание логарифма одинаковы, то значение логарифма будет равно единице.
Логарифм числа, обратного основанию
Логарифм произведения двух положительных чисел
Сумма логарифмов. При умножении логарифмируемых чисел, можно сделать из них сумму 2-х логарифмов, у которых будут одинаковые основания.
Логарифм частного
Логарифм частного. При делении чисел мы получаем разность двух логарифмов с одинаковым основанием.
Логарифм степени положительного числа
Логарифм степени положительного числа равен произведению показателя степени на логарифм этого числа.
Логарифм корня числа
Логарифм корня равен частному от деления логарифма подкоренного числа на показатель корня.
Основание логарифма в степени
Формула перехода к новому основанию
log a x = log b x log b a
log a x = 1 log x a
Производная логарифма
Производная логарифмической функции по основанию равна единице, деленной на произведение подлогарифмической функции на натуральный логарифм основания.
При расчёте производной логарифма необходимо учитывать ложный коэффициент производной, при котором нарастает его гиперболическая составляющая. Это и есть главное условие корректного нахождения производной логарифма. В то же время, нельзя упускать второстепенные составляющие при расчёте. К ним относятся расчеты с применением общей суммы логарифмов, а также пропорциональная составляющая двух вычисляемых логарифмов. Такой подход можно применить не только для вычисления производной натурального логарифма, но и при расчете производной десятичного логарифма при возведении в степень x по основанию a.
График логарифмов
Таким образом можно увидеть изменения логарифма по основанию от 0 до 10. Промежуточным результатом является логарифм по основанию e, которое приблизительно равно 2.72.
Так трафик логарифма по основанию 0 имеет форму прямой линии, а графики десятичного логарифма и натурального логарифма имею гиперболическую форму.
Что такое логарифм
Логарифмы всегда считались сложной темой в школьном курсе математики. Существует много разных определений логарифма, но большинство учебников почему-то используют самые сложные и неудачные из них.
Мы же определим логарифм просто и наглядно. Для этого составим таблицу:
| 2 1 | 2 2 | 2 3 | 2 4 | 2 5 | 2 6 |
| 2 | 4 | 8 | 16 | 32 | 64 |
Итак, перед нами степени двойки. Если взять число из нижней строчки, то можно легко найти степень, в которую придется возвести двойку, чтобы получилось это число. Например, чтобы получить 16, надо два возвести в четвертую степень. А чтобы получить 64, надо два возвести в шестую степень. Это видно из таблицы.
А теперь — собственно, определение логарифма:
Например, 2 3 = 8 ⇒ log2 8 = 3 (логарифм по основанию 2 от числа 8 равен трем, поскольку 2 3 = 8). С тем же успехом log2 64 = 6, поскольку 2 6 = 64.
| 2 1 | 2 2 | 2 3 | 2 4 | 2 5 | 2 6 |
| 2 | 4 | 8 | 16 | 32 | 64 |
| log2 2 = 1 | log2 4 = 2 | log2 8 = 3 | log2 16 = 4 | log2 32 = 5 | log2 64 = 6 |
Если взять калькулятор и посчитать, чему равны такие логарифмы, то получатся очень длинные числа. Взгляните сами:
log2 5 = 2,32192809.
log3 8 = 1,89278926.
log5 100 = 2,86135311.
Такие числа называются иррациональными: цифры после запятой можно писать до бесконечности, и они никогда не повторяются. Если логарифм получается иррациональным, его лучше так и оставить: log2 5, log3 8, log5 100.
Важно понимать, что логарифм — это выражение с двумя переменными (основание и аргумент). Многие на первых порах путают, где находится основание, а где — аргумент. Чтобы избежать досадных недоразумений, просто взгляните на картинку:
Перед нами — не что иное как определение логарифма. Вспомните: логарифм — это степень, в которую надо возвести основание, чтобы получить аргумент. Именно основание возводится в степень — на картинке оно выделено красным. Получается, что основание всегда находится внизу! Это замечательное правило я рассказываю своим ученикам на первом же занятии — и никакой путаницы не возникает.
Как считать логарифмы
С определением разобрались — осталось научиться считать логарифмы, т.е. избавляться от знака «log». Для начала отметим, что из определения следует два важных факта:
Такие ограничения называются областью допустимых значений (ОДЗ). Получается, что ОДЗ логарифма выглядит так: log a x = b ⇒ x > 0, a > 0, a ≠ 1.
Впрочем, сейчас мы рассматриваем лишь числовые выражения, где знать ОДЗ логарифма не требуется. Все ограничения уже учтены составителями задач. Но когда пойдут логарифмические уравнения и неравенства, требования ОДЗ станут обязательными. Ведь в основании и аргументе могут стоять весьма неслабые конструкции, которые совсем необязательно соответствуют приведенным выше ограничениям.
Теперь рассмотрим общую схему вычисления логарифмов. Она состоит из трех шагов:
Вот и все! Если логарифм окажется иррациональным, это будет видно уже на первом шаге. Требование, чтобы основание было больше единицы, весьма актуально: это снижает вероятность ошибки и значительно упрощает выкладки. Аналогично с десятичными дробями: если сразу перевести их в обычные, ошибок будет в разы меньше.
Посмотрим, как работает эта схема на конкретных примерах:
Небольшое замечание к последнему примеру. Как убедиться, что число не является точной степенью другого числа? Очень просто — достаточно разложить его на простые множители. И если такие множители нельзя собрать в степени с одинаковыми показателями, то и исходное число не является точной степенью.
Задача. Выясните, являются ли точными степенями числа: 8; 48; 81; 35; 14.
8 = 2 · 2 · 2 = 2 3 — точная степень, т.к. множитель всего один;
48 = 6 · 8 = 3 · 2 · 2 · 2 · 2 = 3 · 2 4 — не является точной степенью, поскольку есть два множителя: 3 и 2;
81 = 9 · 9 = 3 · 3 · 3 · 3 = 3 4 — точная степень;
35 = 7 · 5 — снова не является точной степенью;
14 = 7 · 2 — опять не точная степень;
Заметим также, что сами простые числа всегда являются точными степенями самих себя.
Десятичный логарифм
Некоторые логарифмы встречаются настолько часто, что имеют специальное название и обозначение.
Например, lg 10 = 1; lg 100 = 2; lg 1000 = 3 — и т.д.
Отныне, когда в учебнике встречается фраза типа «Найдите lg 0,01», знайте: это не опечатка. Это десятичный логарифм. Впрочем, если вам непривычно такое обозначение, его всегда можно переписать:
lg x = log10 x
Все, что верно для обычных логарифмов, верно и для десятичных.
Натуральный логарифм
Существует еще один логарифм, который имеет собственное обозначение. В некотором смысле, он даже более важен, чем десятичный. Речь идет о натуральном логарифме.
Не будем углубляться, что это за число и зачем нужно. Просто помните, что e — основание натурального логарифма:
ln x = log e x
Таким образом, ln e = 1; ln e 2 = 2; ln e 16 = 16 — и т.д. С другой стороны, ln 2 — иррациональное число. Вообще, натуральный логарифм любого рационального числа иррационален. Кроме, разумеется, единицы: ln 1 = 0.
Для натуральных логарифмов справедливы все правила, которые верны для обычных логарифмов.
Основные свойства логарифмов
Логарифмы, как и любые числа, можно складывать, вычитать и всячески преобразовывать. Но поскольку логарифмы — это не совсем обычные числа, здесь есть свои правила, которые называются основными свойствами.
Эти правила обязательно надо знать — без них не решается ни одна серьезная логарифмическая задача. К тому же, их совсем немного — все можно выучить за один день. Итак, приступим.
Сложение и вычитание логарифмов
Итак, сумма логарифмов равна логарифму произведения, а разность — логарифму частного. Обратите внимание: ключевой момент здесь — одинаковые основания. Если основания разные, эти правила не работают!
Эти формулы помогут вычислить логарифмическое выражение даже тогда, когда отдельные его части не считаются (см. урок «Что такое логарифм»). Взгляните на примеры — и убедитесь:
Поскольку основания у логарифмов одинаковые, используем формулу суммы:
log6 4 + log6 9 = log6 (4 · 9) = log6 36 = 2.
Основания одинаковые, используем формулу разности:
log2 48 − log2 3 = log2 (48 : 3) = log2 16 = 4.
Задача. Найдите значение выражения: log3 135 − log3 5.
Снова основания одинаковые, поэтому имеем:
log3 135 − log3 5 = log3 (135 : 5) = log3 27 = 3.
Как видите, исходные выражения составлены из «плохих» логарифмов, которые отдельно не считаются. Но после преобразований получаются вполне нормальные числа. На этом факте построены многие контрольные работы. Да что контрольные — подобные выражения на полном серьезе (иногда — практически без изменений) предлагаются на ЕГЭ.
Вынесение показателя степени из логарифма
Теперь немного усложним задачу. Что, если в основании или аргументе логарифма стоит степень? Тогда показатель этой степени можно вынести за знак логарифма по следующим правилам:
Несложно заметить, что последнее правило следует их первых двух. Но лучше его все-таки помнить — в некоторых случаях это значительно сократит объем вычислений.
Разумеется, все эти правила имеют смысл при соблюдении ОДЗ логарифма: a > 0, a ≠ 1, x > 0. И еще: учитесь применять все формулы не только слева направо, но и наоборот, т.е. можно вносить числа, стоящие перед знаком логарифма, в сам логарифм. Именно это чаще всего и требуется.
Избавимся от степени в аргументе по первой формуле:
log7 49 6 = 6 · log7 49 = 6 · 2 = 12
Задача. Найдите значение выражения:
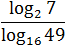
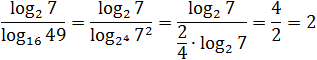
Думаю, к последнему примеру требуются пояснения. Куда исчезли логарифмы? До самого последнего момента мы работаем только со знаменателем. Представили основание и аргумент стоящего там логарифма в виде степеней и вынесли показатели — получили «трехэтажную» дробь.
Теперь посмотрим на основную дробь. В числителе и знаменателе стоит одно и то же число: log2 7. Поскольку log2 7 ≠ 0, можем сократить дробь — в знаменателе останется 2/4. По правилам арифметики, четверку можно перенести в числитель, что и было сделано. В результате получился ответ: 2.
Переход к новому основанию
Говоря о правилах сложения и вычитания логарифмов, я специально подчеркивал, что они работают только при одинаковых основаниях. А что, если основания разные? Что, если они не являются точными степенями одного и того же числа?
На помощь приходят формулы перехода к новому основанию. Сформулируем их в виде теоремы:
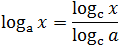
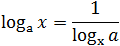
Из второй формулы следует, что можно менять местами основание и аргумент логарифма, но при этом все выражение «переворачивается», т.е. логарифм оказывается в знаменателе.
Эти формулы редко встречается в обычных числовых выражениях. Оценить, насколько они удобны, можно только при решении логарифмических уравнений и неравенств.
Впрочем, существуют задачи, которые вообще не решаются иначе как переходом к новому основанию. Рассмотрим парочку таких:
Задача. Найдите значение выражения: log5 16 · log2 25.
Заметим, что в аргументах обоих логарифмов стоят точные степени. Вынесем показатели: log5 16 = log5 2 4 = 4log5 2; log2 25 = log2 5 2 = 2log2 5;
А теперь «перевернем» второй логарифм:
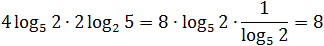
Поскольку от перестановки множителей произведение не меняется, мы спокойно перемножили четверку и двойку, а затем разобрались с логарифмами.
Задача. Найдите значение выражения: log9 100 · lg 3.
Основание и аргумент первого логарифма — точные степени. Запишем это и избавимся от показателей:
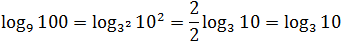
Теперь избавимся от десятичного логарифма, перейдя к новому основанию:
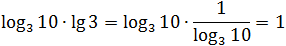
Основное логарифмическое тождество
Часто в процессе решения требуется представить число как логарифм по заданному основанию. В этом случае нам помогут формулы:
В первом случае число n становится показателем степени, стоящей в аргументе. Число n может быть абсолютно любым, ведь это просто значение логарифма.
Подобно формулам перехода к новому основанию, основное логарифмическое тождество иногда бывает единственно возможным решением.
Задача. Найдите значение выражения:
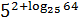
Заметим, что log25 64 = log5 8 — просто вынесли квадрат из основания и аргумента логарифма. Учитывая правила умножения степеней с одинаковым основанием, получаем:
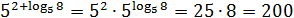
Если кто-то не в курсе, это была настоящая задача из ЕГЭ 🙂
Логарифмическая единица и логарифмический ноль
В заключение приведу два тождества, которые сложно назвать свойствами — скорее, это следствия из определения логарифма. Они постоянно встречаются в задачах и, что удивительно, создают проблемы даже для «продвинутых» учеников.
Вот и все свойства. Обязательно потренируйтесь применять их на практике! Скачайте шпаргалку в начале урока, распечатайте ее — и решайте задачи.
Источники информации:
- http://sigma-center.ru/logarithm
- http://cos-cos.ru/math/75/
- http://skysmart.ru/articles/mathematic/logarifmy
- http://yourrepetitor.ru/chto-takoe-logarifm-kak-poschitat-logarifm-svojstva-logarifmov-primery-resheniya-logarifmov/
- http://youclever.org/book/logarifmy-1/
- http://zaochnik.com/spravochnik/matematika/vyrazhenija/preobrazovanie-vyrazhenij-s-ispolzovaniem-svojstv/
- http://urokmatematiki.ru/reference-information/formuly/formuly-i-svoystva-logarifmov.php
- http://www.berdov.com/docs/logarithm/what/
- http://www.berdov.com/docs/logarithm/basic_properties/