функция y f x называется периодической если существует такое число t 0 что
Периодическая функция
Периодическая функция — это функция, значения которой не изменяются при добавлении к значениям её аргумента некоторого числа T (отличного от нуля).
Функция y=f(x) называется периодической, если существует такое число T≠0, что для любого x из области определения этой функции выполняются равенства:
Число T называют периодом функции y=f(x).
Из определения следует, что значения x-T и x+T также входят в область определения функции y=f(x).
Свойства периодических функций
1) По определению периодической функции для любого x из области определения y=f(x) если T — период функции, то f(x-T)= f(x)=f(x+T).
2) Для любого x из области определения y=f(x) если T1 — период функции, то
Так как T2 также является периодом функции y=f(x), то для аргумента x-T1
Следовательно, число T1+T2 является периодом функции y=f(x).
3) Это свойство непосредственно вытекает из свойства 2, если T взять в качестве слагаемого n раз.
4) Если T — период функции f(x), то для аргумента kx+b
Значит число T/k — период функции f(kx+b).
5) Эти свойства следуют непосредственно из определения.
Например, для суммы f(x) и g(x):
Из свойства 3 следует, что каждая периодическая функция имеет бесконечно много периодов.
Если среди всех периодов функции y=f(x) существует наименьший положительный период, то его называют главным (или основным) периодом функции.
Примеры периодических функций
1) Поскольку для любого x выполняются равенства
то функции y=sin x и y=cos x являются периодическими с периодом T=2π.
2) Так как для любого x из области определения функции y=tg x выполняется равенство
tg (x-π)=tg x =tg (x-π), то y=tg x — периодическая функция с периодом T=π.
Аналогично, y=ctg x — периодическая функция с периодом T=π.
3) Так как для любого действительного числа x и любого рационального числа k выполняется равенство D(x+k)=D(x), то функция Дирихле D(x) — периодическая с периодом T=k, где k∈Q, k≠0.
Поскольку k — любое рациональное число, невозможно его указать наименьшее положительное значение. Следовательно, функция Дирихле не имеет главного периода.
4) Рассмотрим частный случай линейной функции y=b, b — действительное число (b∈R). Эта функция определена на множестве действительных чисел и при любых значениях аргумента принимает единственное значение y=b, то есть для любого действительного числа m (m∈R), y(x)=y(x+m)=b.
Значит y=b — периодическая функция с периодом T=m, где m∈R, m≠0.
Так как m — любое действительное число, оно не имеет наименьшего положительного значения. Поэтому функция y=b не имеет главного периода.
5) Так как для любого действительного x и любого целого k выполняется равенство
Наименьшим положительным целым числом является единица. Следовательно, T=1 — главный период функции y=
Главный период функций y=sin x и y=cos x T=2π.
Главный период функций y=tg x и y=ctg x T=π.
Если T — период функции y=sin x, то sin (x-2π)=sin x = sin (x-2π) для любого x.
То есть любой период функции y=sin x имеет вид 2πn, n∈Z.
Наименьшее положительное значение это выражение принимает при n=1 и оно равно T=2π.
Таким образом, 2π — главный период функции y=sin x.
Аналогично доказываются утверждения о главном периоде функций y=cos x, y=tg x и y=ctg x.
Из 4-го свойства периодических функций непосредственно следует, что для функций y=sin (kx+b) и y=cos (kx+b) (k≠0) наименьший положительный период
а для функций y=tg (kx+b) и y=ctg (kx+b) (k≠0) наименьший положительный период
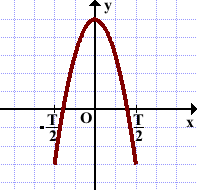
График периодической функции повторяется через промежутки длиной T (на оси Ox).
Дана часть графика
промежутке длиной T.
Чтобы построить график функции, выполняем параллельный перенос этой части графика вдоль оси Ox на ±T, ±2T,… :
Уроки математики и физики для школьников и родителей
суббота, 4 сентября 2021 г.
Урок 5. Периодичность тригонометрических функций
Из этого определения сразу следует, что если Т – период функции
– также периоды функций. Значит у периодической функции бесконечно много периодов.
Чаще всего (но не всегда) среди множества положительных периодов функции можно найти наименьший. Его называют основным периодом .
График периодической функции состоит из неограниченно повторяющихся одинаковых фрагментов.
у = х – [х] , где [х] – целая часть числа. Если к произвольному значение аргумента этой функции добавить 1 , то значение функции от этого не изменится :
Следовательно, при любом значении х
sin (α + 360 ° ) = sin α
Таким образом, функции sin α и cos α от прибавления к аргументу α одного полного оборота ( 2π или 360 ° ) не меняют своих значений.
где k – любое целое число.
Следовательно, функции sin α и cos α – периодические.
Наименьшее положительное число, от прибавления которого к любому допустимому значению аргумента не изменяется значение функции, называется периодом функции.
В самом деле, пусть α – произвольный угол, составленный с осью Ох подвижным радиусом ОМ единичной окружности.
отсюда следует, что значения tg α и с tg α не изменяются, если к углу α прибавить любое число полуоборотов:
где k – любое целое число.
вычисляются по формуле
равен наименьшему числу, при делении которого на T 1 и T 2 получаются целые числа.
Найти период функции
не существует, так как такого числа, при делении которого на 2π и на 2 получались бы целые числа, нет.
Периода не существует.
Доказать следующее утверждение :
Так как тангенс – периодическая функция с минимальным периодом 20 ∙ 180 ° , то получим :
Доказать следующее утверждение :
Так как косинус – чётная и периодическая функция с минимальным периодом 2π , то получим :
сos (–13π) = сos 13π = сos (π + 6 ∙ 2π) = сos π = –1.
Доказать следующее утверждение :
Так как синус – нечётная и периодическая функция с минимальным периодом 20 ∙ 360 ° , то получим :
Найти основной период функции
Пусть Т основной период функции, тогда:
так как 2 πk период синуса, то получим :
sin (7х + 7 t ) = sin (7х + 2 πk ),
Найти основной период функции
Пусть Т основной период функции, тогда:
со s 0,3х = со s 0,3(х + t ) = со s (0,3х + 0,3 t )
так как 2 πk период косинуса, то получим :
Найти период функции :
y = 5 sin 2 x + 2 ctg 3х.
Наименьшее число, при делении которого на
Найти период функции :
Находим периоды слагаемых. Период функции
Очевидно, что период заданной функции равен
Найти период функции :
Периода у заданной функции не существует, так как нет такого числа, при делении которого на 2 и на π одновременно получались бы целые числа.
Найти период функции :
Приведём к общему знаменателю периоды :
Тогда наименьшее общее кратное (НОК) будет :
Теперь найдём период заданной функции :
Математика. Периодичность тригонометрических функций.
Периодической называется функция, которая повторяет свои значения через какой-то регулярный интервал, то есть не меняющая своего значения при добавлении к аргументу фиксированного ненулевого числа (периодафункции): существует такое ненулевое число TT (период), что на всей области определения функции выполняется равенство f(x)=f(x+T).f(x)=f(x+T).
Тригонометрические функции (синус, косинус, тангенс, котангенс) являются периодическими.
Периодичность функций sin φ и cos φ
Предположим, что вектор ОА = (х, у) единичной длины образует с осью абсцисс угол φ.
Если сделать полный оборот вектора ОА вокруг точки О против часовой стрелки, то получится угол φ + 360°. Но вектор ОА при этом займет первоначальное положение, а потому координаты его х и у не изменятся.

у = sin φ = sin(φ + 360°),
x = cos φ = cos (φ+ 360°).
Эти соотношения показывают, что значения функций sin φ и cos φ не изменяются, если их аргумент, увеличить на 360°.
Пусть f(х) есть некоторое выражение, зависящее от переменной величины х. (Например, f(х) = x 2 , f(х) = sin x и т. д.)
Тогда равенство y = f(х)
Определяет у как функцию аргумента х.
Если при любых допустимых значениях аргумента х
где Т — некоторое отличное от нуля число, то функция f (x) называется периодической, а число Т — ее периодом.
Согласно этому определению функции sin x и cos х являются периодическими с периодом Т = 360°.
При n полных оборотах вектора ОА против часовой стрелки образуется угол φ + 360°n, а по часовой стрелке — угол φ — 360°n. В каждом из этих случаев координаты х и у вектора не изменяются, а потому не изменяются sin φ и cos φ.
Таким образом, cos φ = cos (φ + 360°n),
sin φ = sin (φ + 360°n), (1)
где n — любое целое число (положительное, отрицательное или нуль).
Можно доказать, что любая периодическая функция (а не только sin φ и cos φ) имеет бесконечное множество периодов.
Говоря о периоде функции, удобно из бесконечного множества всех ее периодов иметь в виду какой-нибудь один вполне определенный период. Обычно выделяют наименьший положительный период функции.
Из всех рассмотренных выше периодов функции sin φ наименьшим положительным периодом является угол в 360°. Но, может быть, существует еще меньший угол, который мы просто упустили из виду, но который, Также является периодом функции sin φ? Чтобы решить этот вопрос, предположим, что наименьший положительный период функции sin φ равен Т. Тогда при любом φ
sin (φ + Т) = sin φ.
В частности, при φ = 0 получаем: sinТ = sin 0° = 0.
Составляет ли он период функции sin φ? Если бы это было так, то равенство sin (φ + 180°) = sin φ должно было бы выполняться при всех значениях φ. В частности, при φ = 90° мы получили бы
sin 270° = sin 90°.
Аналогично можно доказать, что периодом функции cos φ также является угол в 360° Предлагаем учащимся убедиться в этом самостоятельно.
Периодичность функций tg φ и ctg φ

Следовательно, при любом φ
tg (φ + 180°) = tg φ.
Это означает, что функция tg φ является периодической с периодом 180°. Но будет ли угол в 180° наименьшим жительным периодом этой функции?
Предположим, что наименьший положительный период функции tg φ равен Т. Тогда для всех допустимых значений φ должно быть
tg (φ + Т) = tg φ
В частности, при φ = 0° получаем:
tg Т = tg 0° = 0.
Но тангенс положительного угла равен нулю лишь тогда, когда синус этого угла равен нулю, то есть при Т = 180°, 360°, 540° и т, д. Следовательно, никакой положительный угол, меньший 180°, не может быть периодом функции tg φ. Остается признать, чтб периодом(то есть наименьшим положительным периодом) функции tg φ является угол в 180°.
Аналогично можно доказать, что периодом функции сtg φ также является угол в 180°. Предлагаем учащимся убедиться в этом самостоятельно.
Упражнения
1. Данные выражения преобразовать так, чтобы входящие в них углы были положительными и не превышали 180°:
a) tg 205°; б) tg (—185°); в) ctg 300°; г) ctg (—210°).
2. Данные выражения преобразовать так, чтобы входящие в них углы по абсолютной величине не превышали 90°:
3. Доказать, что угол в 120° является одним из периодов функции у = ctg 3х.
4. Доказать, что любой период Т функции у = ctg х является корнем уравнения
Верно ли обратное утверждение?
О периодических функциях.
Если функция f(x) периодична с периодом Т, то по значениям этой функции на любом отрезке длины Т можно восстановить ее значения на всей числовой прямой.
Действительно, пусть периодическая функция f(x) задана в интервале (а, а + Т), где Т — период этой функции.
Покажем, как можно определить значения этой функции в интервале (а + Т, а + 2T ).
Для любой точки b из этого интервала можно указать точку b‘ из интервала (а, а + T ), отстоящую от b на расстоянии T.
В силу периодичности функции f(x)
f(b) = f( b‘)
Таким образом, по заданным значениям функции f
Итак, задание периодической с периодом Т функции f(x) на любом интервале длины Т дает возможность полностью охарактеризовать ее на всей числовой прямой. Поэтому для исследования функции f(x), периодической с периодом Т, достаточно изучить ее поведение лишь на каком-нибудь интервале длины Т. Например, для исследования функций у = sin φ и у = cos φ достаточно рассмотреть их лишь при 0° Просмотр содержимого документа
«Математика. Периодичность тригонометрических функций.»
Функция y f x называется периодической если существует такое число t 0 что
ФУНКЦИИ И ПРЕДЕЛЫ IX
§ 207. Периодические функции
Функция у = f (x) называется периодической, если существует число Т =/= 0, такое, что при всех значениях х из области определения зтой функции.
Число Т в этом случае называется периодом функции.
Периодическими являются, например, тригонометрические функции у = sin х и у = cos х. Их период равен 2π. Примером периодической нетригонометрической функции может служить функция у = <х>, которая каждому числу х ставит в соответствие его дробную часть*.
* О дробной части числа см. в главе VIII, § 187.
Например, <3,56>= 0,56; <2,01>= 0,01 и т.д. Если к произвольному числу х прибавить 1, то изменится лишь целая часть этого числа; дробная же часть останется прежней. Следовательно, <х + 1> = <х> и потому функция у = <х> является периодической с периодом 1.
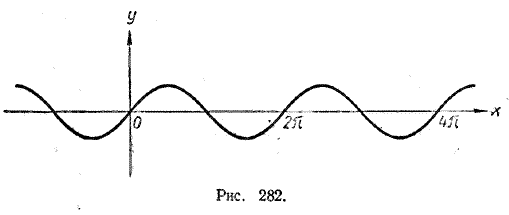
Из равенства f (x + T) = f (x) следует, что все значения функции у = f (x) повторяются с периодом T. Это находит свое отражение и в графическом изображении периодических функций. Так, например, в интервале [0, 2π] синусоида имеет ту же самую форму, что и в интервалах [2π, 4π], [4π, 6π] и т. д. (рис. 282).
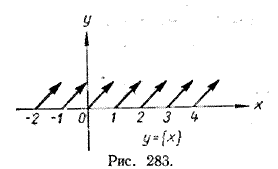
На рисунке 283 представлен график функции у = <х>. Периодичность функции у = <х> обусловливает то, что график ее в интервале [0, 1] имеет ту же самую форму, что и в интервалах [1, 2], [2, 3] и т. д.
Если Т — период функции f (x), то 2Т, 3T, 4Т и т. д. также периоды этой функции.
и т. д. Кроме того, периодом функции f (x) можно считать и любое из чисел: — Т, — 2T, — 3Т и т. д. В самом деле,
и т. д. Итак, если число Т есть период функции f (x), то при любом целом п число пТ также период этой функции. Поэтому всякая периодическая функция имеет бесконечное множество периодов. Например, периодом функции у = sin x можно считать любое из чисел: 2π, 4π, 6π, — 2π, — 4π, а периодом функции у = <х> — любое из чисел: 1, 2, 3, — 1, — 2, — 3 и т. д.
Говоря о периоде функции у = f (x), обычно имеют в виду наименьший положительный период. Так, мы говорим, что периодом функции у = sin х является число 2π, периодом функции у = tg х — число π, периодом функции <х> — число 1 и т. д.
Следует, однако, иметь в виду, что наименьшего положительного периода у периодической функции может и не быть.
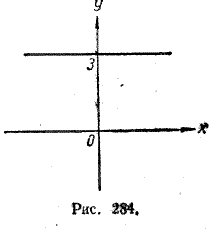
Например, для функции f (x) = 3 (рис. 284) любое действительное число является периодом. Но среди положительных действительных чисел не существует наименьшего. Поэтому и функция f (x) = 3, имея бесконечное множество периодов, не имеет наименьшего положительного периода.
Для каждой из данных функций (№ 1613—1621) найти наименьший положительный период:
1622. Доказать, что сумма и произведение двух функций, периодических с одним и тем же периодом Т, являются функциями, периодическими с периодом Т.
1623*. Докажите, что функция у = sin х + <х>, являющаяся суммой двух периодических функций у = sin х и у = <х>, сама не является периодической.
Не противоречит ли это результату предыдущей задачи?
1624. Как достроить график функции у = f (x), периодической с периодом Т, если он задан лишь в интервале [0, Т]?
Презентация»Периодичность тригонометрических функций»(11 класс,профильное обучение)
Описание презентации по отдельным слайдам:
Периодичность тригонометрических функций 11 класс
Определение: Функция f(x) называется периодической, если существует такое число Т≠0,что для любого х из области определения этой функции значения х+Т и х-Т также принадлежат области определения и выполняются равенства f(x-Т)=f(x)=f(x+Т). Число Т называется периодом функции f(x)
Задача1 Доказать,что f(x)=sinx+1 является периодической с периодом 2π Решение: Функция f(x)=sinx+1 определена на R. f(x+2π)=sin(x+2π)+1=sinx+1=f(x)
Задача 3 Доказать,что f(x)= является периодической с периодом 2π Решение: x f (x+2π)=
Задача 6 Найти наименьший положительный период функции Решение: f(x+Т)=f(x) Наименьший положительный период при n=1
Задача 7 Найти наименьший положительный период функции Решение:
Наименьший положительный период функции при n=1 Т=2π
Задача 8 Найти наименьший положительный период функции Решение: Функция y=cosx имеет период 2π. Функция имеет период
Задача 9 Найти наименьший положительный период функции Решение: Так как функция sin2x имеет период а функция cos3x имеет период то период Т функции будет такое наименьшее положительное число, которое кратно одновременно,т.е.наименьшее общее кратное.Т=2π
Задача 10 Найти наименьший положительный период функции Решение: Так как функция имеет период а функция имеет период то период Т функции будет такое наименьшее положительное число, которое кратно одновременно,т.е наименьшее общее кратное. Т=6π
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
Ищем педагогов в команду «Инфоурок»
Номер материала: ДБ-233469
Международная дистанционная олимпиада Осень 2021
Не нашли то что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Безлимитный доступ к занятиям с онлайн-репетиторами
Выгоднее, чем оплачивать каждое занятие отдельно
Российский совет олимпиад школьников намерен усилить требования к олимпиадам
Время чтения: 2 минуты
Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст
Время чтения: 1 минута
На новом «Уроке цифры» школьникам расскажут о разработке игр
Время чтения: 1 минута
Минпросвещения разрабатывает образовательный минимум для подготовки педагогов
Время чтения: 2 минуты
В Минпросвещения предложили организовать телемосты для школьников России и Узбекистана
Время чтения: 1 минута
В Госдуме предлагают сделать бесплатным проезд на общественном транспорте для детей до 16 лет
Время чтения: 2 минуты
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.