фракталы это что такое простыми словами

Фрактал

Фракта́л (лат. fractus — дроблёный, сломанный, разбитый) — геометрическая фигура, обладающая свойством самоподобия, то есть составленная из нескольких частей, каждая из которых подобна всей фигуре целиком. В математике под фракталами понимают множества точек в евклидовом пространстве, имеющие дробную метрическую размерность (в смысле Минковского или Хаусдорфа), либо метрическую размерность, отличную от топологической.

Содержание

Термин

Слово «фрактал» может употребляться не только как математический термин. Фракталом в прессе и научно-популярной литературе могут называть фигуры, обладающие какими-либо из перечисленных ниже свойств:

Многие объекты в природе обладают фрактальными свойствами, например, побережья, облака, кроны деревьев, снежинки, кровеносная система и система альвеол человека или животных.

Фракталы, особенно на плоскости, популярны благодаря сочетанию красоты с простотой построения при помощи компьютера.

История

Первые примеры самоподобных множеств с необычными свойствами появились в XIX веке (например,функция Больцано, функция Вейерштрасса, множество Кантора). Термин «фрактал» был введён Бенуа Мандельбротом в 1975 году и получил широкую популярность с выходом в 1977 году его книги «Фрактальная геометрия природы».

Примеры

Самоподобные множества с необычными свойствами в математике

Начиная с конца XIX века, в математике появляются примеры самоподобных объектов с патологическими с точки зрения классического анализа свойствами. К ним можно отнести следующие:

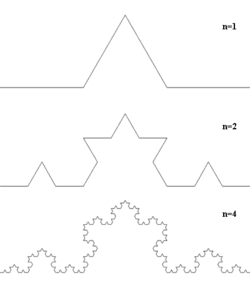
Рекурсивная процедура получения фрактальных кривых

Существует простая рекурсивная процедура получения фрактальных кривых на плоскости. Зададим произвольную ломаную с конечным числом звеньев, называемую генератором. Далее, заменим в ней каждый отрезок генератором (точнее, ломаной, подобной генератору). В получившейся ломаной вновь заменим каждый отрезок генератором. Продолжая до бесконечности, в пределе получим фрактальную кривую. На рисунке справа приведены четыре первых шага этой процедуры для кривой Коха.

Примерами таких кривых служат:

С помощью похожей процедуры получается дерево Пифагора.

Фракталы как неподвижные точки сжимающих отображений

Свойство самоподобия можно математически строго выразить следующим образом. Пусть — сжимающие отображения плоскости. Рассмотрим следующее отображение на множестве всех компактных (замкнутых и ограниченных) подмножеств плоскости:

Можно показать, что отображение является сжимающим отображением на множестве компактов с метрикой Хаусдорфа. Следовательно, по теореме Банаха, это отображение имеет единственную неподвижную точку. Эта неподвижная точка и будет нашим фракталом.

Рекурсивная процедура получения фрактальных кривых, описанная выше, является частным случаем данной конструкции. В ней все отображения — отображения подобия, а — число звеньев генератора.

Для треугольника Серпинского и отображения , , — гомотетии с центрами в вершинах правильного треугольника и коэффициентом 1/2. Легко видеть, что треугольник Серпинского переходит в себя при отображении .

В случае, когда отображения — преобразования подобия с коэффициентами 0″ border=»0″ />, размерность фрактала (при некоторых дополнительных технических условиях) может быть вычислена как решение уравнения . Так, для треугольника Серпинского получаем .

По той же теореме Банаха, начав с любого компактного множества и применяя к нему итерации отображения , мы получим последовательность компактов, сходящихся (в смысле метрики Хаусдорфа) к нашему фракталу.

Фракталы в комплексной динамике

Фракталы естественным образом возникают при изучении нелинейных динамических систем. Наиболее изучен случай, когда динамическая система задаётся итерациями многочлена или голоморфной функции комплексной переменной на плоскости. Первые исследования в этой области относятся к началу 20 века и связаны с именами Фату и Жюлиа.

Нас интересует поведение этой последовательности при стремлении n к бесконечности. Эта последовательность может:

Множества значений z₀, для которых последовательность демонстрирует один конкретный тип поведения, а также множества точек бифуркации между различными типами, часто обладают фрактальными свойствами.

Так, множество Жюлиа — множество точек бифуркации для многочлена F(z)=z 2 +c (или другой похожей функции), то есть тех значений z₀, для которых поведение последовательности <z_n> может резко меняться при сколь угодно малых изменениях z₀.

Другой вариант получения фрактальных множеств — введение параметра в многочлен F(z) и рассмотрение множества тех значений параметра, при которых последовательность <z_n> демонстрирует определённое поведение при фиксированном z₀. Так, множество Мандельброта — это множество всех , при которых <z_n> для F(z)=z 2 +c и z₀ не стремится к бесконечности.

Ещё один известный пример такого рода — бассейны Ньютона.

Популярно создание красивых графических образов на основе комплексной динамики путём раскрашивания точек плоскости в зависимости от поведения соответствующих динамических систем. Например, для дополнения множества Мандельброта можно раскрасить точки в зависимости от скорости стремления <z_n> к бесконечности (определяемой, скажем, как наименьший номер n, при котором |z_n| превысит фиксированную большую величину A.

Биоморфы — фракталы, построенные на основе комплексной динамики и напоминающие живые организмы.

Стохастические фракталы

Природные объекты часто имеют фрактальную форму. Для их моделирования могут применяться стохастические (случайные) фракталы. Примеры стохастических фракталов:

В природе

Применение

Естественные науки

В физике фракталы естественным образом возникают при моделировании нелинейных процессов, таких, как турбулентное течение жидкости, сложные процессы диффузии-адсорбции, пламя, облака и т. п. Фракталы используются при моделировании пористых материалов, например, в нефтехимии. В биологии они применяются для моделирования популяций и для описания систем внутренних органов (система кровеносных сосудов).

Радиотехника

Фрактальные антенны

Использование фрактальной геометрии при проектировании антенных устройств было впервые применено американским инженером Натаном Коэном, который тогда жил в центре Бостона, где была запрещена установка внешних антенн на здания. Натан вырезал из алюминиевой фольги фигуру в форме кривой Коха и наклеил её на лист бумаги, затем присоединил к приёмнику. Коэн основал собственную компанию и наладил их серийный выпуск.

Информатика

Сжатие изображений

Существуют алгоритмы сжатия изображения с помощью фракталов. Они основаны на идее о том, что вместо самого изображения можно хранить сжимающее отображение, для которого это изображение (или некоторое близкое к нему) является неподвижной точкой. Один из вариантов данного алгоритма был использован [источник не указан 779 дней] фирмой Microsoft при издании своей энциклопедии, но большого распространения эти алгоритмы не получили.

Компьютерная графика

Фракталы широко применяются в компьютерной графике для построения изображений природных объектов, таких как деревья, кусты, горные ландшафты, поверхности морей и так далее. Существует множество программ, служащих для генерации фрактальных изображений, см. Генератор фракталов (программа).

Децентрализованные сети

Система назначения IP-адресов в сети Netsukuku использует принцип фрактального сжатия информации для компактного сохранения информации об узлах сети. Каждый узел сети Netsukuku хранит всего 4 Кб информации о состоянии соседних узлов, при этом любой новый узел подключается к общей сети без необходимости в центральном регулировании раздачи IP-адресов, что, например, характерно для сети Интернет. Таким образом, принцип фрактального сжатия информации гарантирует полностью децентрализованную, а следовательно, максимально устойчивую работу всей сети.

Экономика и финансы

А. А. Алмазов в своей книге «Фрактальная теория. Как поменять взгляд на рынки» предложил способ использования фракталов при анализе биржевых котировок, в частности — на рынке Форекс.

Источник

Бесконечность фракталов. Как устроен мир вокруг нас

Мы уже писали о том, как абстрактная математическая теория хаоса нашла применения в самых разных науках – от физики до экономики и политологии. Сейчас мы приведем еще один подобный пример – теорию фракталов. Строгого определения понятия «фрактал» нет даже в математике. Что-то там такое они, конечно, говорят. Но «простому человеку» этого не понять. Как вам, например, такая фраза: «Фрактал – это множество, обладающее дробной хаусдорфовой размерностью, которая больше топологической». Тем не менее, они, фракталы, окружают нас и помогают понять многие явления из разных сфер жизни.

С чего все началось

Фракталами долго никто кроме профессиональных математиков не интересовался. До появления компьютеров и соответствующего софта. Все изменилось в 1982 году, когда в свет вышла книга Бенуа Мандельброта «Фрактальная геометрия природы». Эта книга стала бестселлером, не столько по причине простого и понятного изложения материала (хотя это утверждение весьма относительно – человек, не имеющий профессионального математического образования в ней ничего не поймет), сколько из-за приведенных компьютерных иллюстраций фракталов, которые, действительно, завораживают. Давайте посмотрим на эти картинки. Они, правда, того стоят.

И таких картинок множество. Но какое все это великолепие имеет отношение к нашей реальной жизни и к тому, что окружает нас в природе и повседневном мире? Оказывается, самое прямое.

Но сначала скажем несколько слов о самих фракталах, как геометрических объектах.

Что такое фрактал, если говорить по-простому

Первое. Как они, фракталы, строятся. Это довольно сложная процедура, использующая специальные преобразования на комплексной плоскости (что это такое – знать не надо). Важно только то, что эти преобразования являются повторяющимися (происходят, как говорят в математике, итерациями). Вот в результате этого повторения и возникают фракталы (те, которые вы видели выше).

Второе. Фрактал является самоподобной (точно или приблизительно) структурой. Это значит следующее. Если вы поднесете к любой из представленных картинок микроскоп, увеличивающий изображение, например, в 100 раз, и посмотрите на фрагмент попавшего в окуляр кусочка фрактала, то вы обнаружите, что он идентичен исходному изображению. Если вы возьмете более сильный микроскоп, увеличивающий изображение в 1000 раз, то вы обнаружите, что кусочек попавшего в окуляр фрагмента предыдущего изображения имеет ту же самую или очень похожую структуру.

Из этого следует крайне важный для последующего вывод. Фрактал имеет крайне сложную структуру, которая повторяется на разных масштабах. Но чем больше мы забираемся вглубь его устройства, тем сложнее он становится в целом. И количественные оценки свойств первоначальной картинки могут начинать меняться.

Вот теперь мы оставим абстрактную математику и перейдем к окружающим нас вещам – таким, казалось бы, простым и понятным.

Фрактальные объекты в природе

Береговая линия

Представьте себе, что вы с околоземной орбиты фотографируете некий остров, например Британию. Вы получите такое же изображение, как на географической карте. Плавное очертание берегов, со всех сторон – море.

Узнать протяженность береговой линии очень просто. Возьмите обычную нитку и аккуратно выложите ее по границам острова. Потом, измеряйте ее длину в сантиметрах и, полученное число, умножайте на масштаб карты – в одном сантиметре сколько-то там километров. Вот и результат.

А теперь следующий эксперимент. Вы летите на самолете на высоте птичьего полета и фотографируете береговую линию. Получается картина, похожая на фотографии со спутника. Но эта береговая линия оказывается изрезанной. На ваших снимках появляются небольшие бухты, заливы, выступающие в море фрагменты суши. Все это соответствует действительности, но не могло быть увиденным со спутника. Структура береговой линии усложняется.

Допустим, прилетев домой, вы на основании своих снимков сделали подробную карту береговой линии. И решили измерить ее длину с помощью той самой нитки, выложив ее строго по полученным вами новым данным. Новое значение длины береговой линии превысит старое. И существенно. Интуитивно это понятно. Ведь теперь ваша нитка должна огибать берега всех заливов и бухт, а не просто проходить по побережью.

Заметьте. Мы уменьшили масштаб, и все стало намного сложнее и запутаннее. Как у фракталов.

А теперь еще одна итерация. Вы идете по тому же побережью пешком. И фиксируете рельеф береговой линии. Выясняется, что берега заливов и бухт, которые вы снимали с самолета, вовсе не такие гладкие и простые, как вам казалось на ваших снимках. Они имеют сложную структуру. И, таким образом, если вы нанесете на карту вот эту «пешеходную» береговую линию, длина ее вырастет еще больше.

Да, бесконечностей в природе не бывает. Но совершенно понятно, что береговая линия – это типичный фрактал. Она остается себе подобной, но ее структура становится все более и более сложной при ближайшем рассмотрении (вспомните про пример с микроскопом).

Это воистину удивительное явление. Мы привыкли к тому, что любой ограниченный по размерам геометрический объект на плоскости (квадрат, треугольник, окружность) имеет фиксированную и конечную длину своих границ. А здесь все по-другому. Длина береговой линии в пределе оказывается бесконечной.

Дерево

Дерево воспроизводит само себя, на каждом уровне. При этом его структура постоянно усложняется, но остается себе подобной. Это ли не фрактал?

Кровообращение

А вот кровеносная система человека. Она тоже имеет фрактальную структуру. Есть артерии и вены. По одним из них кровь подходит к сердцу (вены), по другим поступает от него (артерии). А далее, кровеносная система начинает напоминать то самое дерево, о котором мы говорили выше. Сосуды, сохраняя свое строение, становятся все более тонкими и разветвленными. Они проникают в самые отдаленные участки нашего тела, доносят кислород и другие жизненно важные компоненты до каждой клетки. Это типичная фрактальная структура, которая воспроизводит саму себя все в более и более мелких масштабах.

Стоки реки

«Из далека долго течет река Волга». На географической карте это такая голубая извилистая линия. Ну, притоки крупные обозначены. Ока, Кама. А если мы уменьшим масштаб? Выяснится, что притоков этих намного больше. Не только у самой Волги, но и у Оки и Камы. А у них есть и свои притоки, только более мелкие. А у тех – свои. Возникает структура, удивительно похожая на кровеносную систему человека. И опять возникает вопрос. Какова протяженность всей этой водной системы? Если измерять протяженность только основного русла – все понятно. В любом учебнике можно прочитать. А если все измерять? Опять в пределе бесконечность получается.

Наша Вселенная

Конечно, в масштабах миллиардов световых лет, она, Вселенная, устроена однородно. Но давайте посмотрим на нее поближе. И тогда мы увидим, что никакой однородности в ней нет. Где-то расположены галактики (звездные скопления), где-то – пустота. Почему? Почему распределение материи подчиняется иррегулярным иерархическим законам. А что происходит внутри галактик (еще одно уменьшение масштаба). Где-то звезд больше, где-то меньше. Где-то существуют планетные системы, как в нашей Солнечной, а где-то – нет.

Не проявляется ли здесь фрактальная сущность мира? Сейчас, конечно, существует огромный разрыв между общей теорией относительности, которая объясняет возникновение нашей Вселенной и ее устройством, и фрактальной математикой. Но кто знает? Возможно, это все когда-то будет приведено к «общему знаменателю», и мы посмотрим на окружающий нас космос совсем другими глазами.

К практическим делам

Подобных примеров можно приводить много. Но давайте вернемся к более прозаическим вещам. Вот, например, экономика. Казалось бы, причем здесь фракталы. Оказывается, очень даже причем. Пример тому – фондовые рынки.

Практика показывает, что экономические процессы носят зачастую хаотичный, непредсказуемый характер. Существовавшие до сегодняшнего дня математические модели, которые пытались эти процессы описывать, не учитывали одного очень важного фактора – способность рынка к самоорганизации.

Вот тут на помощь и приходит теория фракталов, которые имеют свойства «самоорганизации», воспроизводя себя на уровне разных масштабов. Конечно, фрактал является чисто математическим объектом. И в природе, да и в экономике, их не существует. Но есть понятие фрактальных явлений. Они являются фракталами только в статистическом смысле. Тем не менее симбиоз фрактальной математики и статистики позволяет получить достаточно точные и адекватные прогнозы. Особенно эффективным этот подход оказывается при анализе фондовых рынков. И это не «придумки» математиков. Экспертные данные показывают, что многие участники фондовых рынков тратят немалые деньги на оплату специалистов в области фрактальной математики.

Что же дает теория фракталов? Она постулирует общую, глобальную зависимость ценообразования от того, что было в прошлом. Конечно, локально процесс ценообразования случаен. Но случайные скачки и падения цен, которые могут происходить сиюминутно, имеют особенность собираться в кластеры. Которые воспроизводятся на больших масштабах времени. Поэтому, анализируя то, что было когда-то, мы можем прогнозировать, как долго продлиться та или иная тенденция развития рынка (рост или падение).

Таким образом, в глобальном масштабе тот или иной рынок «воспроизводит» сам себя. Допуская случайные флуктуации, вызванные массой внешних факторов, в каждый конкретный момент времени. Но глобальные тенденции сохраняются.

Вот вам и фракталы! Чем мы дальше уменьшаем масштаб, тем структура фрактала становится все более сложной. Но они воспроизводят себя, так же как это делает фондовый рынок.

Заключение

Почему мир устроен по фрактальному принципу? Ответ, возможно, состоит в том, что фракталы, как математическая модель, обладают свойством самоорганизации и самоподобия. При этом каждая их форма (см. приведенные в начале статьи картинки) сколь угодно сложна, но живет своей собственной жизнью, развивая себе подобные формы. Не так ли и наш мир устроен?

А вот общество. Появляется какая-нибудь идея. Сначала довольно абстрактная. А потом «проникает в массы». Да как-то трансформируется. Но в целом сохраняется. И превращается на уровне большинства людей в целеуказание жизненного пути. Вот тот же СССР. Принял очередной съезд КПСС очередные эпохальные решения, и пошло все это вниз. В более и более мелкие масштабы. Горкомы, парткомы. И так до каждого человека. Повторяющаяся структура.

Конечно, теория фракталов не позволяет нам прогнозировать будущие события. А это вряд ли и возможно. Но на многое то, что нас окружает, и что происходит в нашей повседневной жизни, позволяет смотреть совсем другими глазами. Осознанными.

Источник

Что такое фракталы

Фракталы известны уже почти век, хорошо изучены и имеют многочисленные приложения в жизни. В основе этого явления лежит очень простая идея: бесконечное по красоте и разнообразию множество фигур можно получить из относительно простых конструкций при помощи всего двух операций — копирования и масштабирования

На рубеже XIX и XX веков изучение фракталов носило скорее эпизодический, нежели систематический характер, потому что раньше математики в основном изучали «хорошие» объекты, которые поддавались исследованию при помощи общих методов и теорий. В 1872 году немецкий математик Карл Вейерштрасс построил пример непрерывной функции, которая нигде не дифференцируема. Однако его построение было целиком абстрактно и трудно для восприятия. Поэтому в 1904 году швед Хельге фон Кох придумал непрерывную кривую, которая нигде не имеет касательной, причем ее довольно просто нарисовать. Оказалось, что она обладает свойствами фрактала. Один из вариантов этой кривой носит название «снежинка Коха».

Идеи самоподобия фигур подхватил француз Поль Пьер Леви, будущий наставник Бенуа Мандельброта. В 1938 году вышла его статья «Плоские и пространственные кривые и поверхности, состоящие из частей, подобных целому», в которой описан еще один фрактал — С-кривая Леви. Все эти вышеперечисленные фракталы можно условно отнести к одному классу конструктивных (геометрических) фракталов.

Другой класс — динамические (алгебраические) фракталы, к которым относится и множество Мандельброта. Первые исследования в этом направлении относятся к началу XX века и связаны с именами французских математиков Гастона Жюлиа и Пьера Фату. В 1918 году вышел почти двухсотстраничный труд Жюлиа, посвященный итерациям комплексных рациональных функций, в котором описаны множества Жюлиа — целое семейство фракталов, близко связанных с множеством Мандельброта. Этот труд был удостоен приза Французской академии, однако в нем не содержалось ни одной иллюстрации, так что оценить красоту открытых объектов было невозможно. Несмотря на то что это работа прославила Жюлиа среди математиков того времени, о ней довольно быстро забыли.

В 1982 году вышла книга Мандельброта «Фрактальная геометрия природы», в которой автор собрал и систематизировал практически всю имевшуюся на тот момент информацию о фракталах и в легкой и доступной манере изложил ее. Основной упор в своем изложении Мандельброт сделал не на тяжеловесные формулы и математические конструкции, а на геометрическую интуицию читателей. Благодаря иллюстрациям, полученным при помощи компьютера, и историческим байкам, которыми автор умело разбавил научную составляющую монографии, книга стала бестселлером, а фракталы стали известны широкой публике. Их успех среди нематематиков во многом обусловлен тем, что с помощью весьма простых конструкций и формул, которые способен понять и старшеклассник, получаются удивительные по сложности и красоте изображения. Когда персональные компьютеры стали достаточно мощными то появилось даже целое направление в искусстве — фрактальная живопись, причем заниматься ею мог практически любой владелец компьютера. Сейчас в интернете можно легко найти множество сайтов, посвященных этой теме.

Источник